基于变容二极管的忆阻PID 自适应控制系统设计

程铁栋 ,胡玮剑 ,杨丽荣 ,尹宝勇 ,林 鹏

(1.江西理工大学 电气工程与自动化学院,江西 赣州 341000;2.深圳大学 材料学院,广东 深圳 518060)

忆阻器这一概念于1971 年由蔡少棠教授在原有电路理论的基础上首次提出[1],其物理器件则在2008 年由惠普实验室首次发现[2-3]。忆阻器是一种新型的二端电子器件,其阻值依赖于电荷量和磁通量。由于忆阻器具有天然的阻值记忆能力,它的I-V特性曲线是一种收缩的磁滞回线[4]。忆阻器具有非易失性和纳米级尺寸的特点,在智能控制和人工神经网络等应用中展现出极大的发展潜力。

PID 控制器广泛应用于现代的工业生产过程中。它主要通过在调整比例系数kp、积分系数ki和微分系数kd这三个参数的同时,以PID 的输出和设定值之偏差作为输入,并将输出信号作用在被控对象上来达到控制的目的。PID 控制器具有可靠性强、结构简单等优点,但传统PID 控制器的参数不易整定,且一经确定无法改变,于是将智能控制和PID 相结合的智能PID 控制器受到了更多的关注[5]。

目前,PID 控制器和忆阻器的结构趋于简单化,例如文献[6]提出一种仅用两个CFOA、三个电阻以及两个电容构成的PID 控制器,且该控制器具有独立可调的控制参数;文献[7]设计出一种用纯无源器件构成的忆阻器,进一步降低了忆阻器的研究门槛以及成本。虽然在2013 年就已有文献提出将忆阻器引入PID控制中[5],以实现智能控制的目的,但是目前忆阻PID 的研究成果仍然较少。

为了解决目前传统的PID 控制存在参数调整困难的问题,本文采用忆阻器替换传统PID 电路中的电阻,有效简化了参数调整的过程。并在此基础上,将变容二极管和忆阻器进行了有机整合,即用基于变容二极管的电路实现忆阻器的功能,提出了基于变容二极管的忆阻PID 自适应控制系统,它能够完成参数的自整定,实现智能PID 控制。该方法使得PID 控制器可以应用于更加精密、复杂的制造过程。

1 PID 控制电路

PID 控制电路主要包括比例、积分和微分控制电路三部分,通过对比例系数kp、积分系数ki和微分系数kd的整定,可以改变PID 控制电路的性能以及功能。通过调节kp可以减少系统的响应时间,提高系统的调节精度,kp越大,则系统响应越快,调节精度越高。通过调节ki可以消除系统的余差,ki越大,则系统余差的消除时间越短。通过调节kd可以抵消积分作用产生的不稳定趋势,kd越大,则调节时间越长,抗干扰能力减弱。图1 为PID 控制电路的电路图。其中U1、U2、U3 是型号为EL2210CN 的运算放大器,分别构成比例运算、微分运算和积分运算电路,为PID 控制的三个支路,U4 是型号为TL062ACD 的运算放大器,构成减法运算电路,将三个支路的结果整合并输出。由此可以得到输入信号和输出信号之间的关系以及比例系数、微分系数、积分系数表达式,具体为:

图1 PID 控制电路图Fig.1 Circuit diagram of PID control

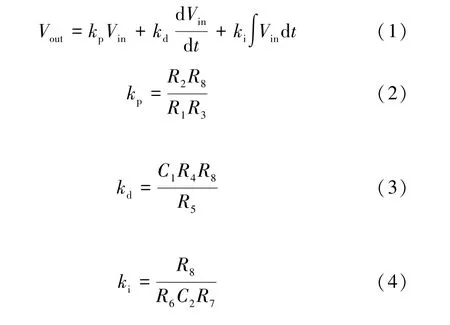
式中:Vin为输入信号;Vout为输出信号。

2 基于变容二极管的忆阻器

2.1 忆阻器的原理

忆阻器(Memristor)主要有电流控制型忆阻器和电压控制型忆阻器,即荷控忆阻器和磁控忆阻器。忆阻器的阻值由加在其两端的电压大小、方向以及持续时间决定,同时具备记忆功能,可以记忆流过它的电荷量或磁通量。同时它也是非易失的,能够保持断电时的阻值直到再次打开电源恢复供电。2008 年惠普实验室发现的荷控忆阻器[2]即由两个金属Pt 电极与夹在其间的两层TiO2薄膜构成,其中一层TiO2薄膜内含有氧空缺,即掺杂层,而另一层为纯TiO2薄膜,即非掺杂层。荷控忆阻器的阻值大小随着掺杂层与非掺杂层的边界移动而改变。磁控忆阻器则是在荷控忆阻器的基础之上推导得到,根据文献[8],荷控忆阻器的阻值公式为:

式中:ROFF和RON分别是TiO2薄膜全为非掺杂层和全为掺杂层时的极限阻值;M(0)为忆阻器的初始阻值;,μV为离子迁移率,D为TiO2薄膜的厚度;c1=。由此可以根据磁通量和电压之间的关系得到电荷和磁通量之间的关系[9],架起电流控制型忆阻器与电压控制型忆阻器的桥梁,进而可以得到磁控忆阻器忆导的表达式:

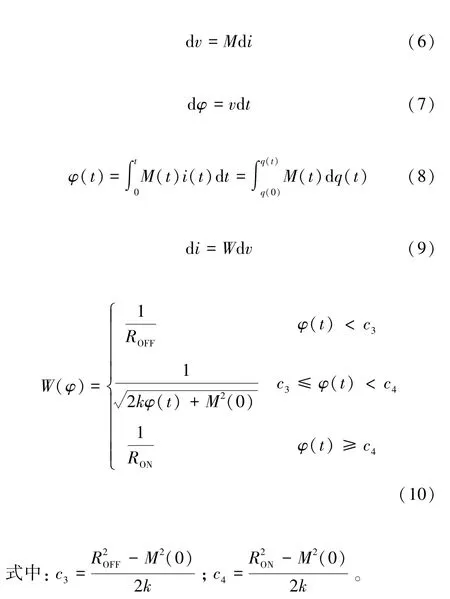
2.2 基于变容二极管的忆阻器模型

变容二极管(Varactor Diodes)是一种电容大小随加在其两端的反向电压的改变而改变的二极管,且反向电压与结电容之间的关系是非线性的。当加一正向偏压时,pn 结的空间电荷区因外加电场与内建电场方向相反而变窄,电容值增大;当加一反向偏压时,pn结的空间电荷区因外加电场与内建电场方向相同而变宽,电容值减小。

根据忆阻器和变容二极管的原理,可以搭建出由三个运算放大器和一个变容二极管构成的磁控忆阻器仿真模型[10],如图2 所示。由于运算放大器具有很大的输入阻抗和很小的输出阻抗,故该磁控忆阻器模型可以与其他电路进行级联[11]。

图2 磁控忆阻器仿真电路Fig.2 Simulation circuit of flux-controlled memristor

在图2 所示的电路中,U1 和U3 是型号为AD844AN 的运算放大器。其中U1 构成积分电路,可以获得相等的磁通量,且根据U1 的性质,流入U1 的电流与流经C1的电流相等,由此可以计算等效的磁通量,其表达式为:

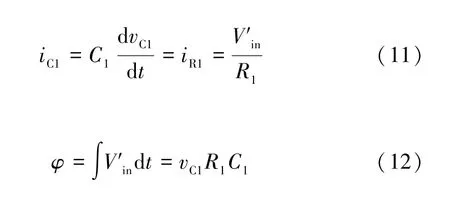
式中:iC1为流经电容C1的电流;vC1为电容C1两端的电压;iR1为流经电阻R1的电流;为输入运放U1 的电压。

U2 是型号为TL084ACD 的运算放大器,构成加减法运算电路,使得变容二极管D1 工作在反向偏压下。根据加减法运算电路的特点,U2 的输出电压可以表示为:

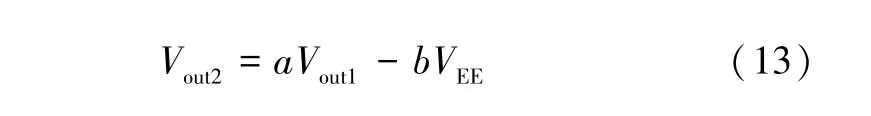
式中:a;Vout1为运放U1 输出的电压;Vout2为运放U2 输出的电压。

通过在该磁控忆阻器两端加上频率为4.5 kHz,幅值为300 mV 的正弦波以及频率为45 kHz,幅值为300 mV 的正弦波,可以观察到I-V波形的变化趋势以及伏安特性曲线,如图3 所示。通过对图3(b)和(c)中的结果进行分析可知,该磁控忆阻器的伏安特性曲线是典型的滞回曲线,且在4.5 kHz 时呈斜“8” 字状,在该频率的十倍频处呈一不自交叉的滞回曲线,体现了忆阻器的频率相关性。实验验证了该磁控忆阻器模型的正确性,并证明了将该忆阻器模型运用到PID 控制电路中的可行性,为下一步研究提供了基础。

3 忆阻PID 控制系统

目前用忆阻器实现PID 控制的M-PID (PID Control System Based on Memristors)主要应用于神经网络方面[12-13],利用忆阻器可作为电子突触的特性[14-15],将其作为可在线学习的模块替换掉原PID 控制器中的一个电阻[16-17],以此达到参数自整定的目的[18]。已经有研究将忆阻器和神经网络PID 控制器相结合[5],把忆阻器作为电子突触嵌入神经网络PID 控制器中,根据输入误差信号的变化来改变其忆阻值,进而改变kp、ki、kd这三个参数,直至输出信号与设定值达到一致。

图4 为忆阻PID 控制器原理图,其中忆阻神经网络构成了在线学习模块,对参数进行动态调整。控制器的输入为误差及误差的导数,经过PID 控制后输出并作用在被控对象上。忆阻器以kp、ki、kd三个系数和PID 控制的输入量为输入,在经过调整之后,把合适的权值输送给下方的PID 控制器,既能体现忆阻PID 控制器的在线学习能力,又能对被控对象进行更有效的控制。

图4 忆阻PID 控制器原理图Fig.4 Schematic of M-PID controller

4 基于变容二极管的忆阻PID 自适应控制系统

4.1 电路模型的搭建

在Multisim 软件中搭建基于变容二极管的忆阻PID 控制系统实验模型,如图5 所示。图5 中的运放U5 用以比较设定值和输出信号,将得到的偏差信号送入PID 控制电路中,M1、M2、M3 内封装有图2 所示的磁控忆阻器电路,信号经过比例-积分-微分运算后输入到磁控忆阻器电路中,使得忆阻器的阻值发生改变,进而改变PID 控制中的kp、ki和kd这三个系数,达到忆阻神经网络的控制效果。电路中的R8起到加快电路响应速度的作用,且能够有效地抑制方波跳变时产生的毛刺。运放U4 构成一个减法运算电路,其保证输出信号与设定值同相的同时将三条支路的信号合成并输出。若M1、M2、M3 的忆阻值发生改变,kp、ki、kd也随之改变,进而达到参数自整定的效果。

图5 基于变容二极管的忆阻PID 自适应控制系统Fig.5 Adaptive M-PID control system circuit based on varactor diode

4.2 Multisim 仿真

对基于变容二极管的忆阻PID 自适应控制系统进行Multisim 仿真实验,各元件参数配置情况如表1 和表2 所示。

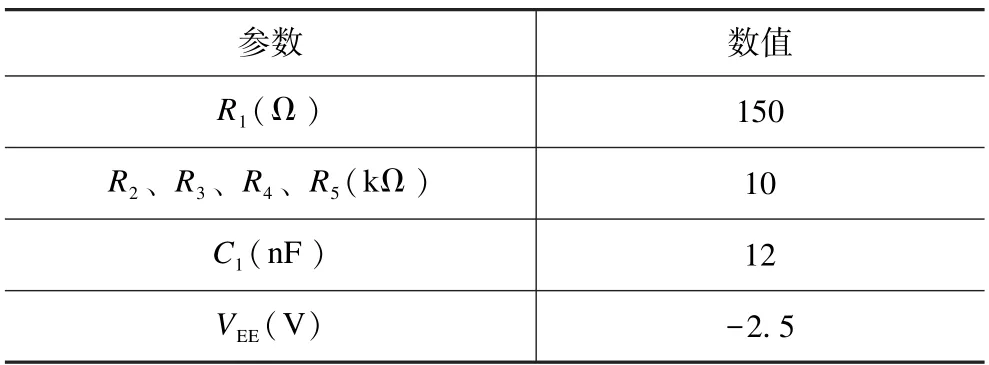
表1 磁控忆阻器电路中各元件参数配置Tab.1 Parameter configuration of each component in the circuit of the flux-controlled memristor

表2 本文提出的M-PID 系统中各元件参数配置Tab.2 Parameter configuration of each component in the M-PID system proposed in this paper

当输入幅值为200 mV,频率为1 kHz 的正弦波、三角波以及方波信号时,可以在模拟示波器中观测到如图6 所示波形。由图6 可知,输出信号波形经过一个短暂的波动之后迅速被调整至与输入信号波形重合,即kp、ki、kd这三个参数在忆阻器的作用下自动调整到合适的值,证明忆阻PID 控制系统具有快速响应并在线学习的特性。同时,根据图6(c)以及图6(d)所显示的忆阻PID 自适应控制系统对方波信号的整定过程来看,在PID 控制电路的输出级添加一个大小合适的电阻(R8)能够有效遏制方波跳变时产生的毛刺,同时加快整定速度。

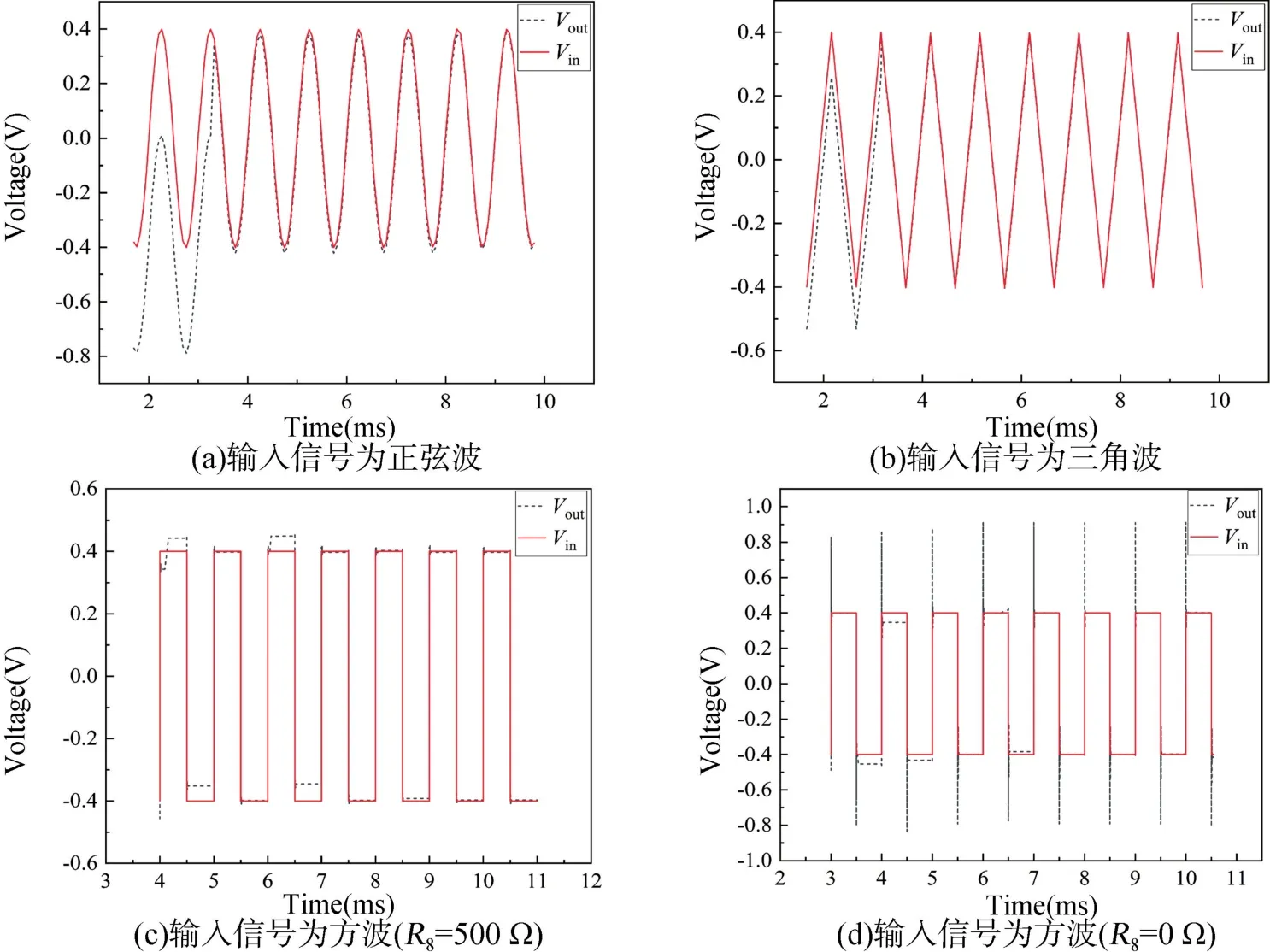
图6 波形的整定过程Fig.6 Waveform setting process

图7 为忆阻PID 和传统PID 对冲激信号的控制效果对比,其中图7(a)、(c)为添加PID 控制电路输出级电阻R8时的整定过程,图7(b)、(d)为未添加PID控制电路输出级电阻R8时的整定过程。根据仿真结果可知R8的添加既增快了电路的响应速度,又减小了超调量,使系统更加稳定,波形更加理想。

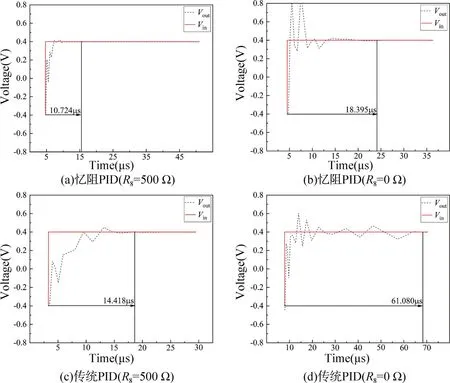
图7 PID 电路对冲激信号的控制作用Fig.7 Control effect of PID circuit on the impulse signal

除仿真之外,还对本文提出的自适应M-PID 控制系统进行了物理实验。按照图5 所示的电路搭建出实际电路,再利用信号发生器输入幅值为700 mV,频率为1 kHz 的正弦波,最后借助示波器观察系统的输出图像。忆阻PID 系统接线图以及正弦波整定的实验结果分别如图8 和图9 所示。此结果表明本文提出的MPID 自适应控制系统能够达到预期效果,实现对输入信号的整定,与仿真结果相符。

图8 忆PID 系统接线图Fig.8 Wiring diagram of M-PID system

图9 输入输出波形比对图Fig.9 Comparison diagram of input and output

本文在已有研究的基础上,讨论了忆阻PID 对三种信号的控制效果,同时对比了忆阻PID 和传统PID对冲激信号的控制效果,进一步论证了本文所提出的基于忆阻器的PID 自适应控制系统能够有效地实现参数的动态调整,具有比传统PID 控制更优良的控制性能。

5 结论

本文建立了基于变容二极管实现忆阻器功能的PID 控制系统的电路模型,进行了Multisim 仿真以及实验,理论推导、仿真与实验结果均验证了方案的可行性与正确性。在电路搭建上,均使用简单的元件,制造方便且容易实现。在参数整定上,适当地添加电阻R8使得系统能更加快速而稳定地将输出信号调整至设定值。在用忆阻器替代原PID 控制电路中的电阻的情况下,根据忆阻器的阻值受到加在其两端电压的大小、方向和时间的影响这一特性,实现了PID 参数的自整定。研究结果可以大大降低PID 参数整定的时间,将繁琐且需要经验的整定过程简化,为更精密、更高效的工业生产控制方法提供了参考。