二维变密度介质中纳米圆柱形空腔对SH波的散射问题研究

雷东侠，尚 童，欧志英

(兰州理工大学理学院，兰州 730050)

许多学者研究了弹性波在层状介质中的传播问题。Daros等人[1-2]采用格林函数法研究了波在连续非均匀介质中的传播问题，证明了颤变公式可以用来推导具有线性速度变化的非均匀介质的基本解。Achenbach[3]根据拓展互易定理，研究了在半空间中剪切模量和质量密度随深度变化的SH波，将速度与波数及剪切模量和质量密度的深度依赖关系的函数联系起来。为了研究非均匀介质中的波传播特性，有人根据复变函数理论，研究了剪切模量和密度是一维变化的SH波散射问题。还有人对SH波在半空间、全空间中密度变化的一系列问题进行了研究。

随着纳米技术的快速发展，许多学者研究了纳米尺度下的波动理论。Fang等人研究了表界面刚度对嵌入在承受反平面剪切波的半空间中的圆柱形纳米非均匀性周围的动应力集中问题。Ou等人在研究单个或两个纳米涂层孔洞时引入波函数展开法，讨论了界面能对模型的影响。

1 理论模型和分析

1.1 模型的分析

如图1所示，在弹性空间中存在一个纳米尺度下二维近似线性非均匀介质的圆柱形空腔，一列稳态入射平面SH波在非均匀介质内沿x轴方向水平传播。

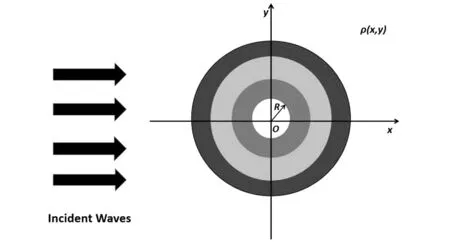
图1 二维变密度介质中纳米圆柱形空腔对SH波的散射Fig.1 Scattering of SH waves by nanocylindrical cavities in the two-dimensional variable density medium

假设介质的剪切模量μ质量密度是二维，且随着x方向和y方向变化而变化，密度的表达式为：

ρ(x,y)=ρ0[4α2(x2+y2)+4αβx+β2]

(1)

其中，ρ0是介质的参考质量密度，α和β是非均匀参数。根据弹性介质的性质，非均匀参数α和β不能同时为0。

据波数k和密度ρ间的关系，波数可表示为：

(2)

1.2 控制方程

考虑到密度的变化，假设存在一个简谐相应且忽略体力，非均匀介质的波动方程可表示为：

(3)

基于复变函数理论，将式(2)代入(3)可得到：

(4)

为了将变系数的Helmholtz方程转化为标准的Helmholtz方程，引入新的复变量：

(5)

将式(5)代入(4)可得：

(6)

2 位移场和应力场

考虑无限大非均匀介质中的位移场和应力场，水平入射波表达式为：

(7)

其中，w0是入射波的振幅。

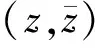
(8)

(9)

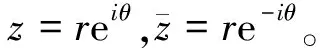
(10)

(11)

将式(7)代入式(10)和(11)，可得到入射波的应力表达式：

(12)

(13)

因介质中存在圆柱形孔洞，则孔洞周围引起的散射波的表达式可写为：

(14)

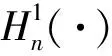
将式(14)代入式(10)和(11)，可得到散射波的应力表达式：

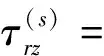
(15)

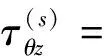
(16)

在非均匀介质中，总波场为：

w=w(i)+w(s)

(17)

3 边界条件

根据表面弹性理论，将各向同性材料的本构关系引入到纳米尺度下，得到其边界条件为：

(18)

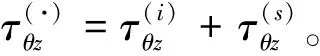
利用方程(18)可求得未知系数An的表达式为：

(19)

将式(19)两边同时乘以e-imθ，且在区间(-π,π)上对角度θ进行积分，可得到有关未知系数An的方程组：

(20)

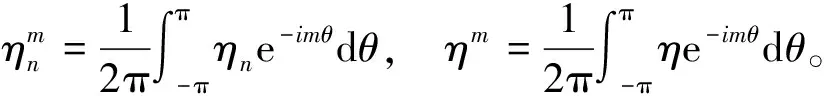
通常用圆形空腔边界处的DSCF来评价动应力集中的程度，其定义为：

(21)

其中，τθz是环向应力，τ0=μk0w0。

4 算例分析

主要研究两个非均匀参数满足β/α<5。根据动应力集中因子的定义可知，考虑表面效应时，两个非均匀参数α和β、入射波波数k0和表面参数s都对DSCF的变化有一定的影响。

由图2可知，与已有的文献结果相比较，当s→0时，动应力集中因子与s=0，即不考虑表面效应时结果是一致的。

图2 当α=0.5，β=1，k0R=1时，表面效应s对DSCF的影响Fig.2 Influence of surface effect s on DSCF when α=0.5, β=1 and k0R=1

图3表示，以低频波数k0=0.1入射时，随着s的增大，动应力集中因子逐渐减小，且不均匀性使DSCF的最值出现在波背面，其最大值出现在θ=π/3和θ=5π/6处，最小值出现在θ=0和θ=π处。

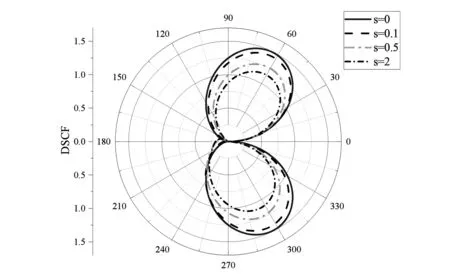
图3 当α=0.4，β=1，k0R=0.1时，表面效应s对DSCF的影响Fig.3 Influence of surface effect s on DSCF when α=0.4, β=1 and k0R=0.1

图4表示以高频波数k0=2入射时，随着s的增大，动应力集中因子变化不规则且出现多个波峰和波谷。最大值随着s的增大逐渐减小，最小值出现在θ=0和θ=π处。

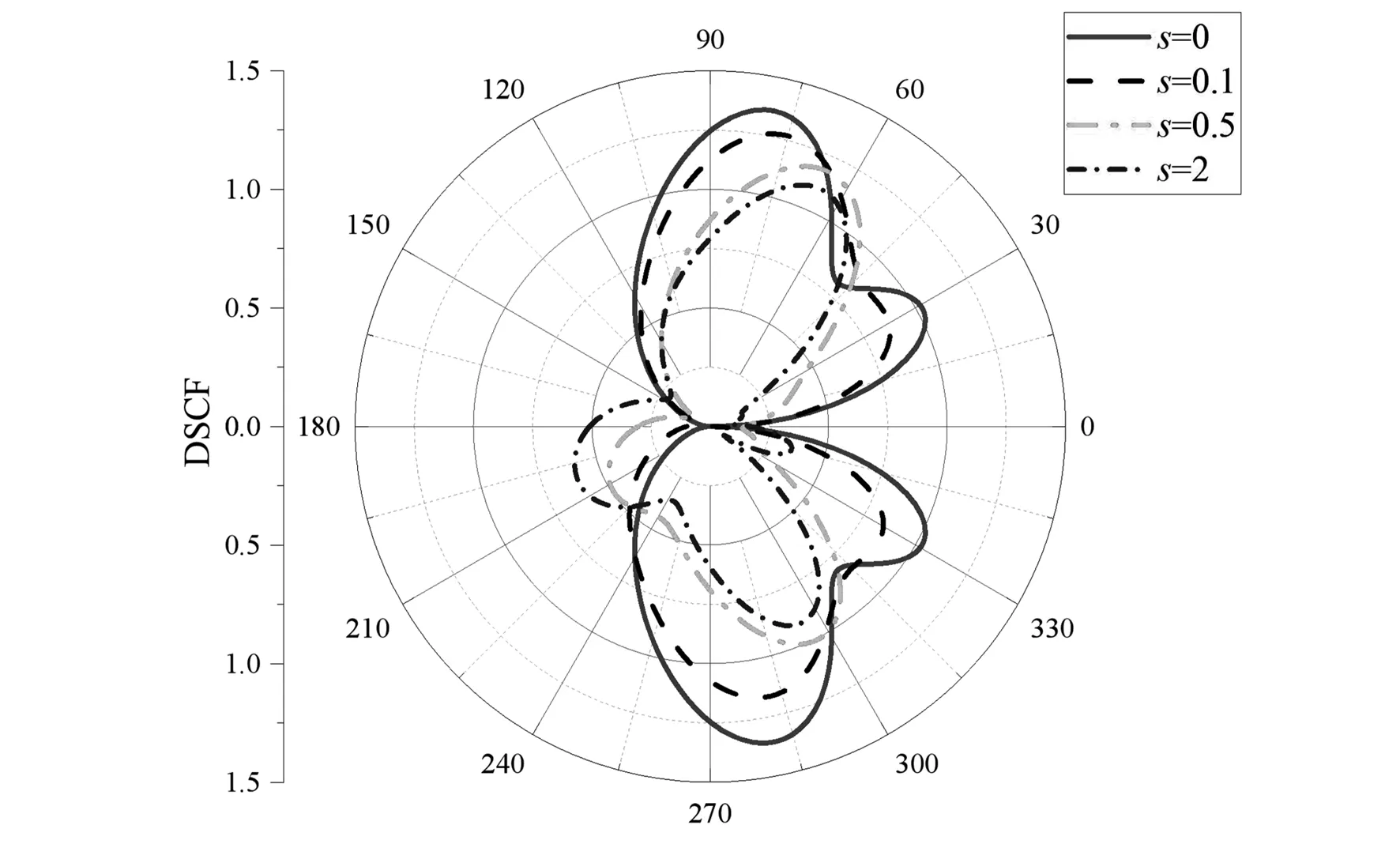
图4 当α=0.4，β=1，k0R=2时，表面效应s对DSCF的影响Fig.4 Influence of surface effect s on DSCF when α=0.4, β=1 and k0R=2

由图5可知，以低频波数k0=0.1入射时，图形关于x轴对称。随着表面参数s的增大，动应力集中因子逐渐减小，且阴影侧的DSCF分布比光照侧的更复杂。

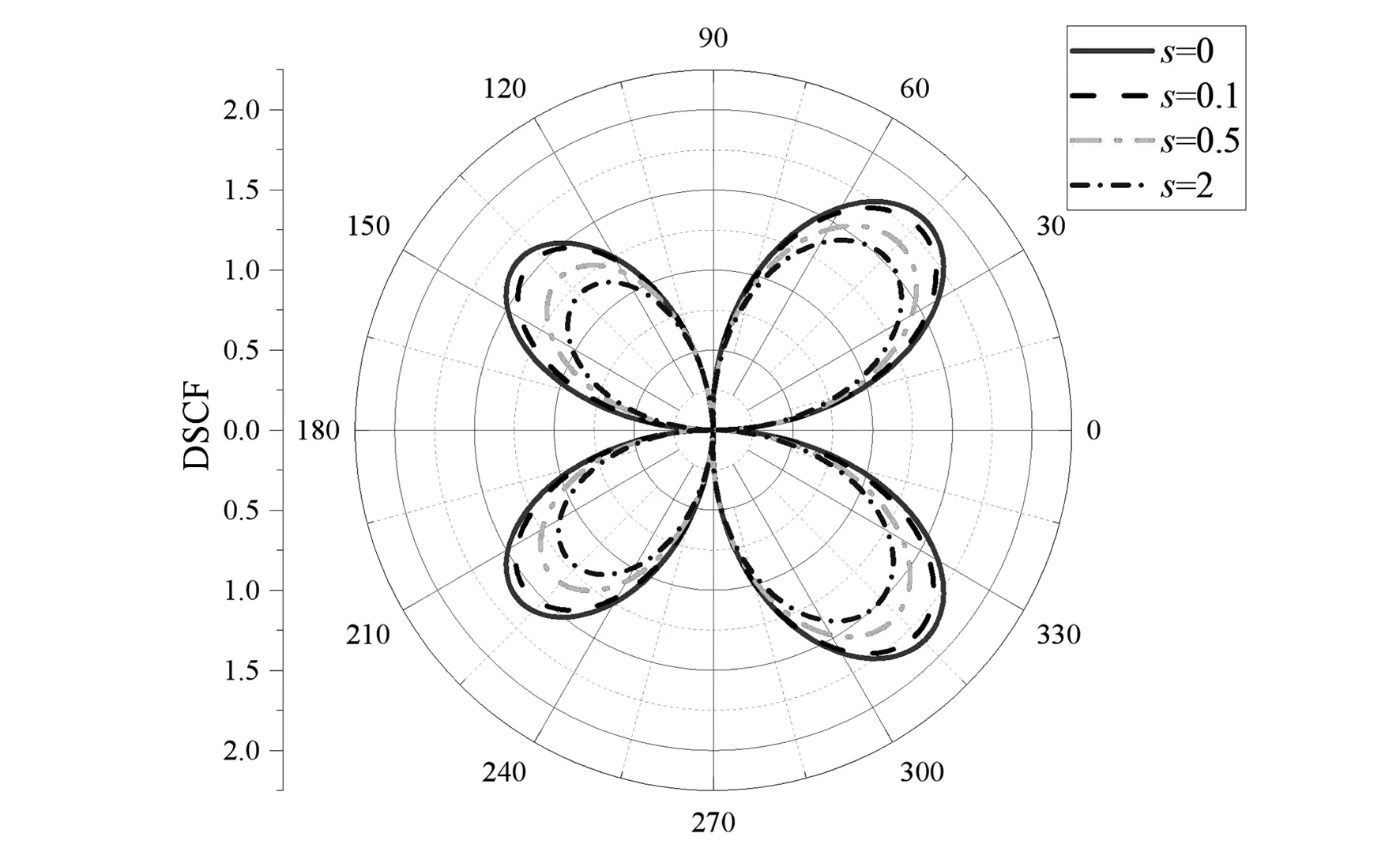
图5 当α=1.5，β=0.2，k0R=0.1时，表面效应s对DSCF的影响Fig.5 Influence of surface effect s on DSCF when α=1.5, β=0.2 and k0R=0.1

由图6可知，以高频波数k0=2入射时，随着表面参数s的增大，动应力集中因子先减小后增大且变化复杂，出现多个峰值和波谷。

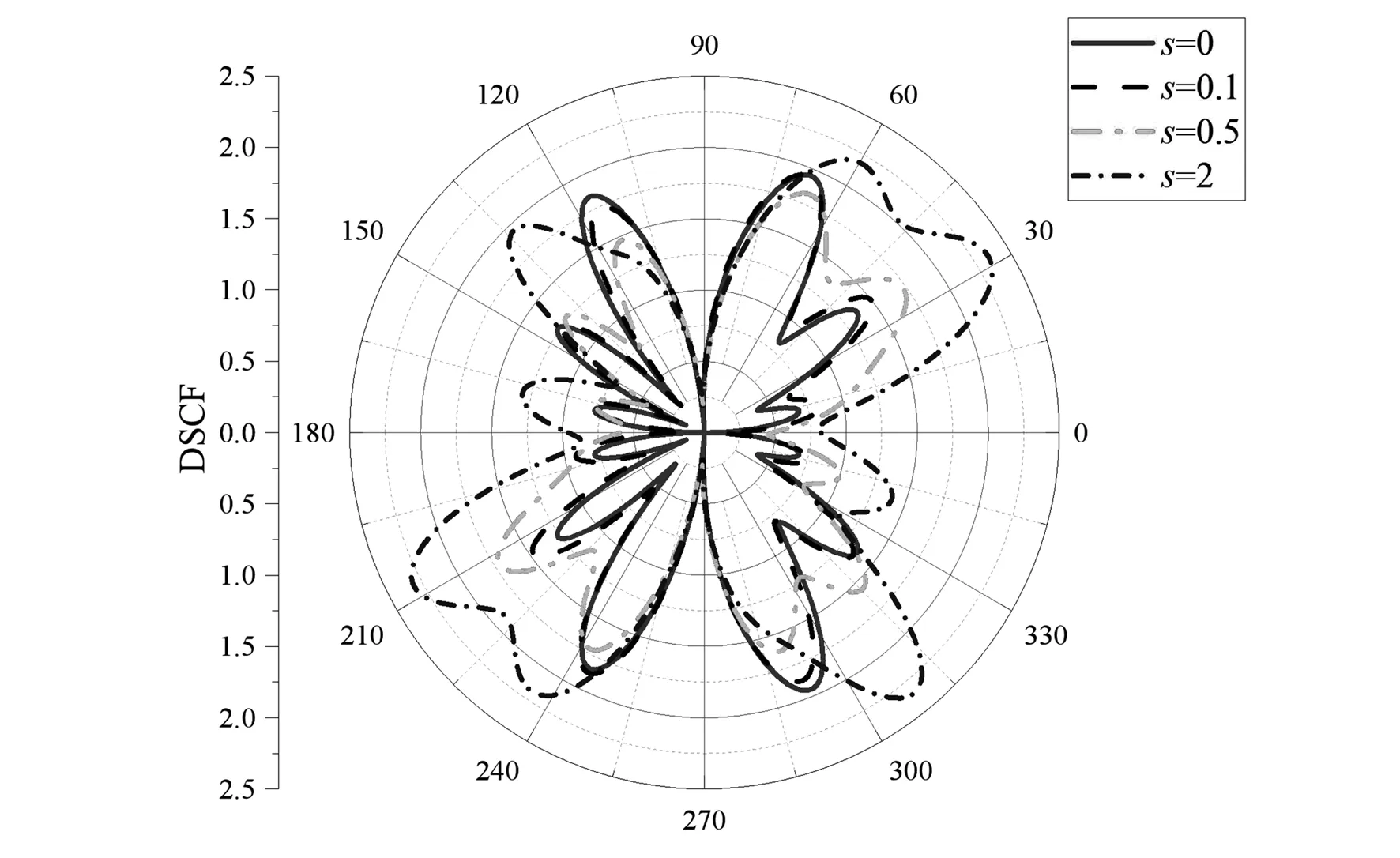
图6 当α=1.5，β=0.2，k0R=2时，表面效应s对DSCF的影响Fig.6 Influence of surface effect s on DSCF when α=1.5, β=0.2 and k0R=2

5 结论

利用复变函数法和保角变化，讨论了纳米尺度下二维近似线性非均匀介质中圆柱形空腔对平面SH波的散射问题。通过数值模拟可得：在纳米尺度下圆柱形空腔边界处的应力集中变化显著，当非均匀参数α<β时，表面参数s越小，动应力集中因子分布比较均匀；当非均匀参数α>β时，表面参数s越大，动应力集中分布越复杂。在纳米尺度下，随着波数的增加，动应力集中因子逐渐向阴影侧移动。