基于长期监测数据与LSTM 网络的滑坡位移预测

梁 阳 肖 婷 胡 程 任世聪 曾 亮

（1.重庆三峡学院电子与信息工程学院，重庆 404000；2.北京理工大学重庆创新中心，重庆 401135；3.北京理工大学信息与电子学院雷达技术研究所，北京 100081；4.重庆市地质矿产研究院，重庆 400042）

1 引言

我国滑坡灾害具有分布广、频率高和危害大的特点，每年都会造成不同程度的人员伤亡和严重的经济损失，因此需要加强对滑坡的预测预警。滑坡地质灾害的形成原因较为复杂，滑坡影响因素多、随机性强、预测难度大，难以及时定点地准确预报。因此，最好的方式是在监测地质环境变化的同时结合现有的长期数据进行有效地预测，对滑坡环境的变化情况和发展趋势进行分析，同时计算气象环境变化与滑坡发生的内在联系，进行有效地提前预防。

滑坡预测预报研究发展阶段大致可分为20 世纪60 年代的自然现象，经验方程预测时期，20 世纪80 年代的统计分析预测时期和20 世纪90 年代的非线性及综合预测时期［1］。进入21 世纪，随着多项式拟合、神经网络、极限学习机、机器学习等智能算法的发展和逐步成熟，其在非线性映射能力和高精度函数逼近等方面表现出优越性能，于是地质灾害预警领域也开始大量应用［2］。其中，静态预测模型多用于以往的实验中，虽然其表现出良好的非线性映射能力，但将滑坡位移预测视为静态回归问题忽略了滑坡演化的动态系统本质［3］。为了避免稳态模型对滑坡预测造成的这一问题，可以考虑采用动态模型来对滑坡进行预测。在目前的动态系统模型中，RNN（Recurrent Neural Network）是一种经典的算法，主要用于处理时间序列的数据，已大量应用于搜索查询、股票市场分析和用户视频推送等方面［4］。但是由于RNN 内部结构的问题，在传播过程中会出现梯度消失或梯度爆炸问题。由此，学术界提出了长短期记忆（Long Short-Term Memory，LSTM）神经网络来解决这个问题。在传播过程中会出现梯度消失或梯度爆炸问题，而长短期记忆（Long Short-Term Memory，LSTM）神经网络的出现有效地解决了这个问题，相比于RNN，LSTM 结构中新增了遗忘门、输入门和输出门等单元［5-6］，解决了神经网络固有的易陷入局部最小值、梯度缺失问题［7］。因此，本文选取LSTM 和RNN 两个神经网络模型进行位移预测及模型性能对比。

以八字门滑坡为例，先将滑坡点总位移分解为受自身地质条件演化控制的趋势项和受降雨、库水位变化等外界诱发因素影响的的周期项；然后，采用多项式最小二乘法拟合预测趋势项位移，利用LSTM 和RNN神经网络模型预测周期项位移。对总预测值进行误差分析，结果表明LSTM 模型通过控制历史信息的流向，在面对数十年的长时间序列时表现出明显更好的预测能力。

2 滑坡位移时间序列分析

2.1 滑坡累计位移分解

研究表明，滑坡体和周围不动岩体自身的层位，地质结构结合其周围的气象环境条件共同导致了滑坡体的变形位移，其位移表现为非线性函数，滑坡累计位移时间曲线可表达为：

式中：X(t)为位移时间序列；s(t)为趋势项位移，是滑坡位移序列变动总方向，它受滑坡体和周围不动岩体的自身地质结构影响；c(t)为周期项位移，它是由降雨、库水位变化等因素决定的；ε(t)为随机项位移，一般为监测点的局部扰动等，视为曲线噪音，一般不考虑［8］。

2.2 模型介绍

（1）循环神经网络模型（RNN）

RNN 模型通过对序列型的数据进行高度拟合从而建立深度模型。在传统的全连接神经网络的结构中，神经元之间互不影响，并没有直接联系，神经元与神经元之间相互独立。而在RNN 结构中，隐藏层的神经元开始通过一个隐藏状态所相连，通常会被表示为h(t)。其结构图如图1所示。

上图为经典的RNN 结构，其运算过程可以表示为：

式中y(t)表示神经网络的输出，h(t-1)表示前一个时间点的状态；x(1)，x(2)...x(t)为序列数据，即神经网络的输入；U、W、V是参数矩阵，b、c是偏置项，f是激活函数，通常采用”热撸”、tanh 函数作为激活函数，用Softmax将输出转换成各个类别的概率。

RNN 在反向传导时，需要计算各个参数的梯度，在梯度一步步传播过程中，随着参数U、W、V的主特征值在1 附近的变化与积累，最终会导致梯度的消失或爆炸，无法学到远距离的数据。所以RNN单元在面对长序列数据时，很容易便遭遇梯度弥散，使得RNN 只具备短期记忆，即RNN 面对长序列数据，仅可获取较近的序列的信息，而对较早期的序列不具备记忆功能，从而丢失信息。因此，Hochreiter 和Schmidhuber 提出了一种改进方法，即长短时记忆网络（LSTM）9］。

（2）长短时间记忆网络模型（LSTM）

LSTM 是一种特殊的RNN，相比于RNN，LSTM模型新增加了记忆单元、细胞状态、输入门、遗忘门和输出门等机制，从而有效地解决了RNN 的短期依赖瓶颈［10］，其结构图如图2所示。

如图2 所示，LSTM 的关键是整个单元的状态（绿色框代表一个单元或者一个细胞），其中横穿单元的水平线称为细胞链，它起着计算的作用。细胞中的信息状态直接穿过细胞链，在细胞链中存在一些线性相互作用，以保持信息的容易传递。使用细胞链的优点是可以直接添加或删除信息。因此，可以选择性地允许信息通过并与sigmoid 神经元层或逐点乘法操作一起使用。LSTM 有三个值用于保护和控制单元状态的门：

遗忘门：首先，LSTM 是计算从细胞状态中丢弃哪些信息。这个决定是由遗忘门做出的。在单元状态为Ct-1时，该门可以获得值为1 或0 的ht-1（前一层的隐藏状态）和xt的输出。1 表示“完全保留”，0表示“完全放弃”。

输入门：这个步骤是计算有多少新信息应该添加到这个细胞状态中。实现这一目标有两个步骤：首先，将前一层隐藏状态的信息和当前输入的信息传递到sigmoid函数中去；然后使用前一层隐藏状态的信息和当前输入的信息来计算需要更新的信息并生成一个向量。总之，通过组合这两个步骤来更新单元的状态。我们将旧状态Ct-1乘以ft（ft是需要丢弃的信息），然后Ct-1更新为Ct。ft的方程，Ct-1，Ct为分别如下。

式中，ht-1是前一层的输出，xt是输入向量，σ是sigmoid 函数，Wf是ft和it的系数矩阵，bf是ft的偏置，bi是it的偏置，Wc是的系数矩阵，bc是的偏置，Ct-1是来自前一块的存储器，Ct是来自当前块的存储器。

输出门：最终，应该确定输出值，此输出取决于细胞状态。首先，计算一个sigmoid 函数来决定输出单元的哪个部分，接下来，通过前一层的隐藏状态选择细胞状态，并将其与sigmoid 函数的输出相乘。

式中，Wo是ot的系数矩阵，bo是ot的偏置，ht是当前模块的输出。

输入层有三个输入，隐藏层有10 个神经元，输出层预测一个值。激活函数用sigmoid 迭代100 次。批量损失函数为全批量学习损失函数和交叉熵。

式中T是周期时间，yi是样本数据，ht是LSTM 的输出。

2.3 模型预测精度指标

本文采用均方根误差（Root mean square error，RMSE）和相关性系数（Correlation coefficient，R）评价模型预测精度［11］，绝对误差和相对误差用于评价最终预测结果的误差。

式中：xi和分别为真实值和预测值；和分别为真实值和预测值的平均值；N为样本数。

3 八字门滑坡

3.1 滑坡地质概况

八字门滑坡地处湖北省秭归县归州镇，三峡库区香溪河右岸河口处。香溪河在此呈南北走向，与长江近直交，三峡水库已淹没滑坡体前缘55～156 m段［12］。滑坡体呈撮箕状展布于岸坡坡脚，分布高程139～280 m 西高东低，向东倾斜［13］。滑坡于1981 年出现复活迹象，此后几年周边相继出现了4 条大裂缝。1987 年到1989 期间暴雨导致变形加剧，坡面房屋开裂，公路出现裂缝。20 世纪末长江爆发洪水，该区域186 m 高程处产生多条裂缝，路面下沉，房屋遭到破坏。21 世纪初，随着三峡水库不断地蓄水，滑坡各部相继出现多条裂缝，原有裂缝进一步加剧变形。此后滑坡自身的地质结构发生改变，稳定性变差，在降雨和库水位下降时期，滑坡多次出现裂缝，公路路面发生小型坍塌。

3.2 监测数据分析

八字门滑坡从20 世纪80 年代开始，陆续发生位移变形现象。在三峡工程逐步推进的同时，库水位也逐渐升高，其对八字门滑坡体及其周围不动岩体的地质结构造成了一定程度的影响，导致滑坡的不稳定性增加。为了了解掌握滑坡的具体情况和监控其位移变形，滑体上设置有ZG109，ZG110，ZG111，ZG112四个监测点，如图3所示。

如图4 所示，2003～2013 年间4 个监测点的位移时间序列。2006 年库水位从145 m 升至155 m，导致海拔较低的ZG109 监测点失效。2008 年库水位上升至175 m，导致ZG112 监测点失效。ZG110和ZG111 都具有明显的阶跃式位移特性，变形更大的ZG111 监测点能更好地代表滑坡的危险状态，因此，选取该点的位移时间曲线进行位移预测分析。监测点数据的总时间跨度为2003 年7 月～2013 年12 月，将2011 年8 月以前的数据作为建模数据，预测2011 年9 月～2012 年12 月的位移值，最后将预测值与真实值进行比对。

图5为ZG111监测点累计位移量与库水位和降雨量的关系图，ZG111 的监测点年变形量在122～268 mm 之间，且变形量逐年增加，其中2008 年到2009 年变化量最大为268 mm。库水位自2006 年9 月开始呈周期性波动，年变化量在20.14～28.43 m 之间，其中2011 年变化量最大为28.43 m。每年7 月份左右是库水位的谷值，12 月份左右是库水位的峰值。降雨量呈季节性周期性变化，每年4到9月份为强降雨季节，7、8月降雨量最大，1、2月降雨量最小。

4 滑坡位移预测

4.1 趋势项预测分析

将滑坡总位移分解为趋势项和周期性，趋势项采用一次移动平均法计算。一次移动平均法是把时间序列数据按一定的长度计算一次移动平均，能较好地反映时间序列的趋势及其变化，计算公式如下：

式中Mi为时间序列，为原序列中Mt所对应的趋势项提取值，t=N，N+1，...，n，分段点数N为跨越期数，即由远及近用于计算的数据个数，用于平滑随机性带来的偏差，一般N=6～200。本文分析的周期项主要由库水位，降雨量等以年为周期进行波动的因子组成，同时文章中N以月为单位，所以为了更好地平滑趋势项和保留周期项的特征，本文N取12。提取出趋势项位移后，利用三次多项式函数对其进行拟合及预测［14］。由于库水位从2008 年开始正式周期性波动，数据以2008 年9 月为界线分两段进行拟合（图6、图7），采用第二段的拟合公式进行预测（公式（17））。趋势项预测值如图8 所示，预测值与真实值高度重合。

拟合函数为：

4.2 周期项预测分析

周期项影响因素主要为前期总位移、降雨量和库水位，将影响因素初步用10 个指标因子表示，采用神经网络建立指标因子与周期项位移值的关系模型。为避免不相干因子对建模产生的干扰，首先需要对特征因子进行筛选。

4.2.1 特征因子筛选

本文通过Pearson相关性分析来筛选特征因子，Pearson 相关系数是衡量两个连续变量间关系的大小和方向的，其取值范围为［-1，1］，-1代表负相关，1代表正相关，0则代表不存在相关关系。相关系数越接近0，相关关系越弱；越接近-1 或1，相关关系越强，公式如下。

其中，X，Y为两个等长向量，N为向量元素个数。

对2003年7月～2011年8月的103组数据（每组都是一个周期项对应10个特征因子）作各特征因子与周期项的Pearson相关性分析，相关性分析见表1。表中当月降雨量、前三月库水位变化量两个特征因子相关性较低，说明降雨入渗、软化岩土体参数等存在一定滞后性，近两月的库水位波动对滑坡应力状态改变明显。因此，剔除当月降雨量和前三月库水位变化量，剩下的8个作为有效特征因子。

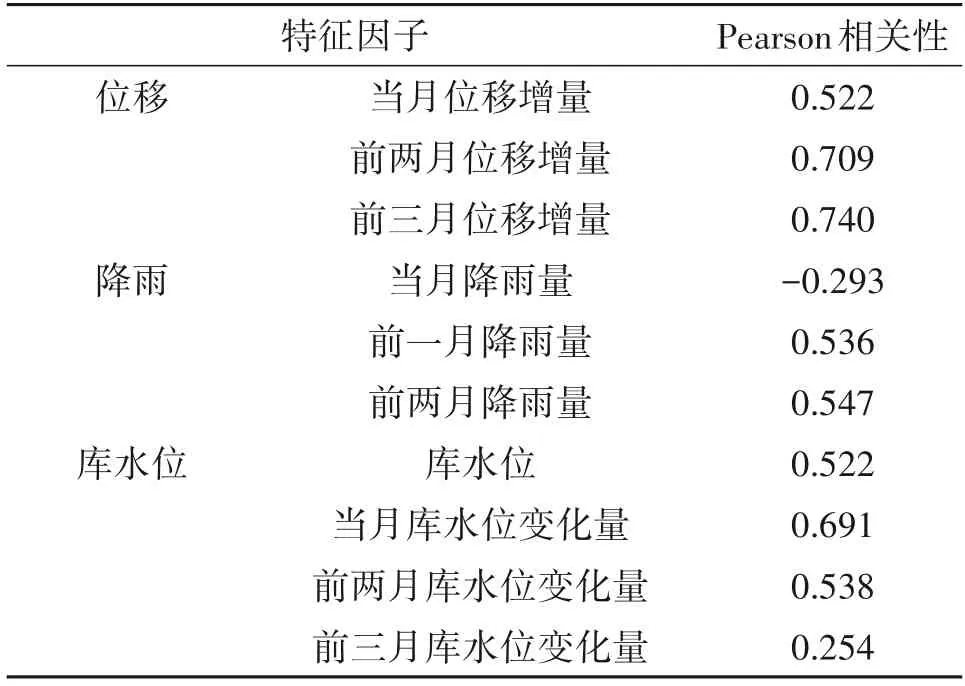
表1 影响因子筛选结果Tab.1 Screening results of influencing factors

4.2.2 建立模型

本文实验样本集属于小规模样本集，为了保证预测集的样本数量满足实验要求，把样本数据按6∶2∶2 的比例分为训练集，验证集和预测集。其中训练集通过不断地迭代训练来得到合理的神经网络的参数，验证集用于检验训练后的模型是否符合要求，测试集用于评价神经网络的性能。LSTM 和RNN模型预测结果，分别如图9、图10所示。对预测段的预测值与真实值进行误差分析可知（表2），LSTM 模型的预测结果误差约10 mm，相关系数R高达0.985，预测值及趋势线与真实情况几乎吻合（图9）。RNN模型的预测结果误差约24 mm，相关系数R为0.741，预测值及趋势线与真实情况存在一定偏差（图10）。由预测结果误差图（图11）可以看出，本案例的预测结果LSTM 模型明显优于RNN 模型，因此周期项预测结果采用LSTM 模型所计算的预测值。

表2 误差分析Tab.2 Error analysis

4.3 累计位移预测

将预测得到的趋势项与周期项进行数值相加，即得到预测的总位移值（图12）。由图可知，预测曲线与真实曲线高度吻合，在库水位与强降雨期间，准确预测到了位移发生的时间和阶跃位移量。

5 结论

文章以滑坡位移这一非线性系统为对象，采用神经网络模型，结合十年监测数据，通过选取合适的指标因子，对八字门滑坡ZG111 监测点进行位移预测，并主要得出如下结论：

（1）八字门滑坡位移呈台阶式阶跃上升，位移阶跃期与强降雨期、库水位下降期高度重合，说明降雨、库水位波动是该滑坡位移主要影响因素。

（2）由指标因子与周期项的相关性分析可知，“当月降雨量”、“前三月库水位变化量”两个因子与周期项的相关性较低，说明降雨入渗、软化岩土体参数等存在一定滞后性，当月降雨量主要影响下月位移，库水位波动对滑坡应力状态的影响时间为两个月。

（3）滑坡的位移不仅受到外界因素的影响（如：降雨、库水位），还受到前期位移量的影响，位移时间序列具有时间指向性。与传统的循环神经网络（RNN）相比，长短时间记忆网络（LSTM）模型通过控制历史信息的流向，更适用于有时间顺序的长时间序列。