一种超载与地震组合作用下的边坡滑动计算方法研究

刘赟 徐媛 魏占玺

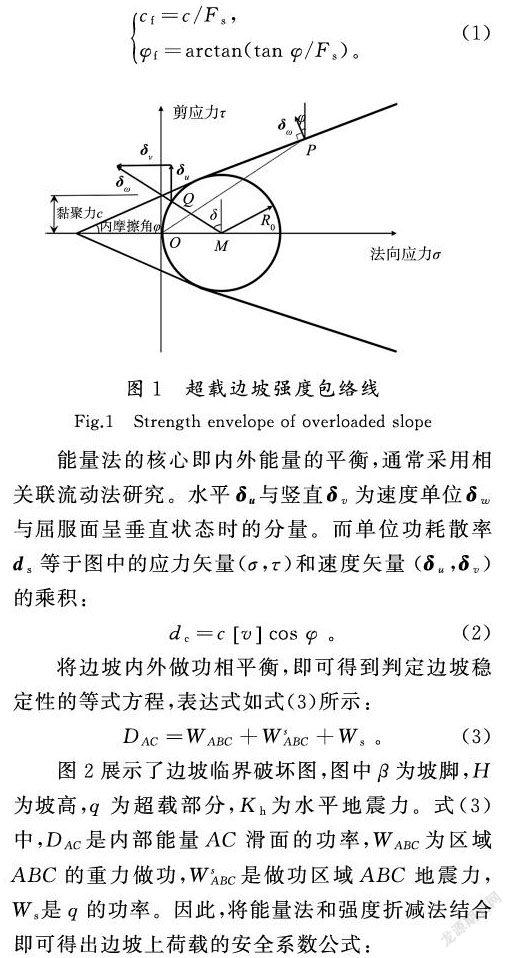
摘 要：为了探究极端环境条件对边坡稳定性的影响，针对超载与地震组合作用下的致滑因素进行了分析，基于能量法与强度折减法推导了组合作用下的安全系数Fs以及临界加速度系数Ks，采用Matlab内嵌序列二次优化法求解极限值，并与经典解比较，最后选取汶川地震、熊本地震2条代表性地震波对边坡位移进行计算。结果表明，1）验证结果准确，推导方法可用于求解边坡临界系数;2）在2种破坏条件下，矿山边坡的稳定性受到显著影响，其安全系数Fs或者临界加速度系数Ks降低了近乎一半;3）应用Newmark法计算位移结果显示在地震荷载的作用下，超载边坡产生了数十倍的滑落距离。研究揭示了地震及顶部超载2种极端条件对边坡稳定性的显著影响，研究结果可为边坡稳定性评估提供参考。

关键词：岩土力学;地震边坡;超载作用;极限分析;位移

中图分类号：U419   文献标识码：A   DOI： 10.7535/hbgykj.2022yx01008

Abstract：In order to explore the influence of extreme environmental conditions on the stability of the slope，the sliding factors under the combined action of overload and earthquake were analyzed and the safety factor Fs and the critical acceleration Ks under the combined action were derived based on the energy method and the strength reduction method.The limit value was solved by using sequence quadratic optimization method embedded in Matlab，and was verified with the classical solution.Finally，two representative seismic waves of Wenchuan earthquake and Kumamoto earthquake were selected to calculate the slope displacement.The results show that： 1） the verification results are accurate，and the derivation method of this research can be used to solve the critical coefficient of slope;2） under the two failure conditions，the stability of the mine slope is significantly affected，and its safety factor Fs or critical acceleration factor Ks is reduced by nearly half;3） combining with Newmark method，the displacement results are calculated，which indicate that under the action of seismic load，the overloaded slope has produced dozens of times the sliding distance.The study reveals the significant impact of two extreme conditions of earthquake and top overload on slope stability.The results can provide certain reference opinions for the evaluation of slope stability in engineering construction.

Keywords：geotechnical mechanics;seismic slope;overlord;limit analysis;displacement

大型建設工程中的很多项目面临着矿山边坡稳定性问题的困扰，基于理论假设的边坡稳定性分析方法较为经典的有：圆弧滑动法、瑞典条分法、毕肖普法、摩根斯坦-普莱斯法、简布法、斯班塞法和沙尔玛法等。

圆弧滑动法是将边坡的滑动面假设为圆弧形，通过求解圆弧总体的抗滑力矩与下滑力矩之比来获得边坡的稳定安全系数[1]。瑞典条分法可以看作是圆弧滑动法的一个改进，其主要思想是将圆弧滑动面以上的坡体分割成多个竖向的条块，在忽略条块间的相互作用后，通过极限平衡思想求解出边坡的稳定安全系数。BISHOP[2]通过对瑞典条分法进行改进，将条块间的相互作用考虑在内，并重新定义了边坡的安全系数为滑动面上的抗滑剪切强度和滑动面上的剪切应力之比，通过这一方法可以更为准确地求解边坡的稳定安全系数。BISHOP对边坡稳定安全系数的定义被多种理论分析法所采用。

前述的边坡稳定性分析方法均将边坡的滑动面形状假设为圆弧形，许多学者对相关影响参数进行了分析[3-4]，但圆弧滑动法更加适合对均质边坡的研究。对于极限分析法，沈珠江[5]对简单破坏条件下2D边坡的严格上限理论进行了总结，并给出了详细的解决方法。

考虑地震作用对矿山边坡的影响，拟静力法计算简便、理论清晰，在研究中被广泛采用，但此方法未考虑地震的动态过程[6]，存在显著不足。NEWMARK[7]针对此问题提出了滑动位移计算的方法，考虑边坡的屈服加速度和受地震动影响下的滑动位移，以此分析边坡稳定状态。之后不断有学者针对NEWMARK所提方法进行改进[7-10]。

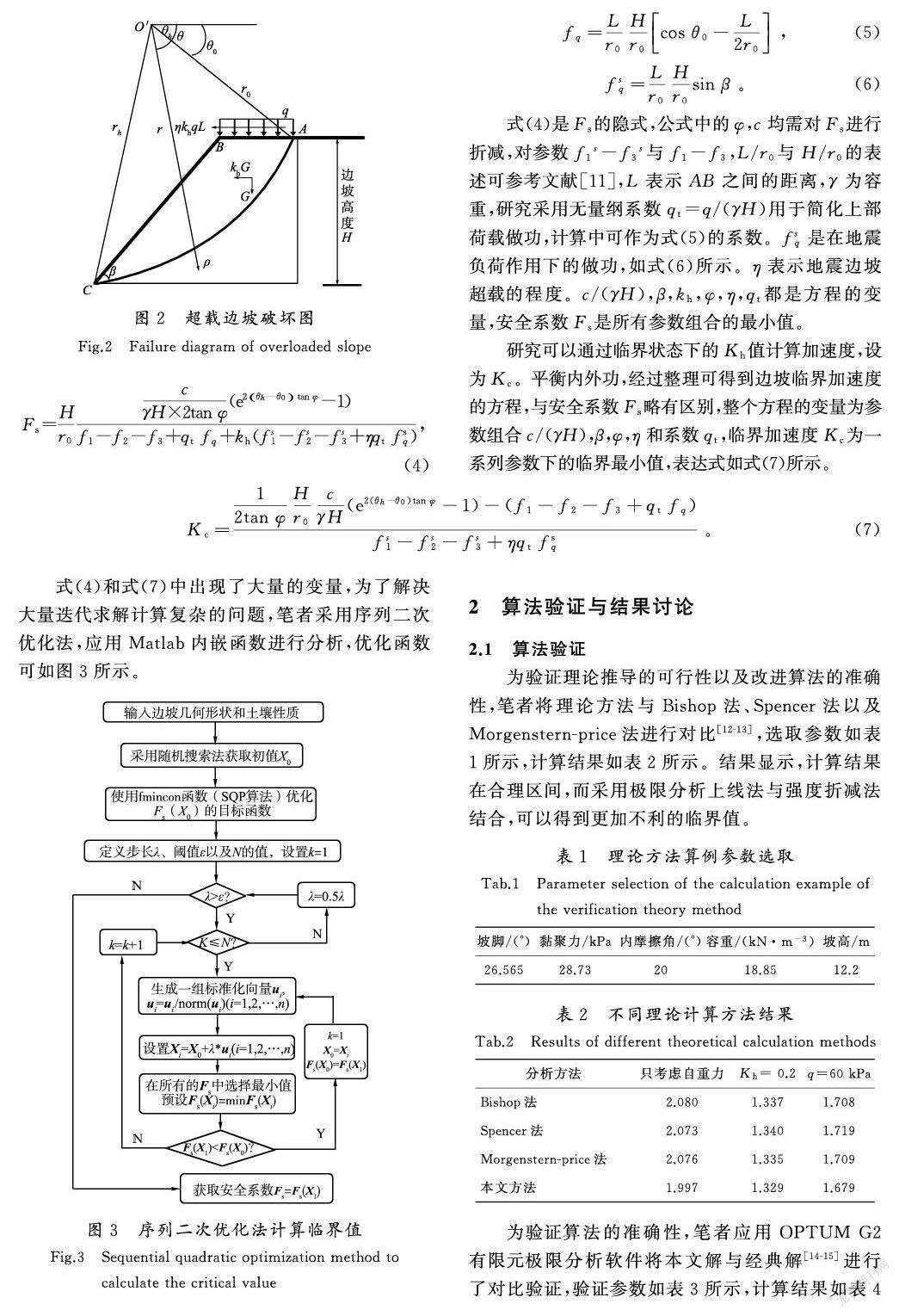
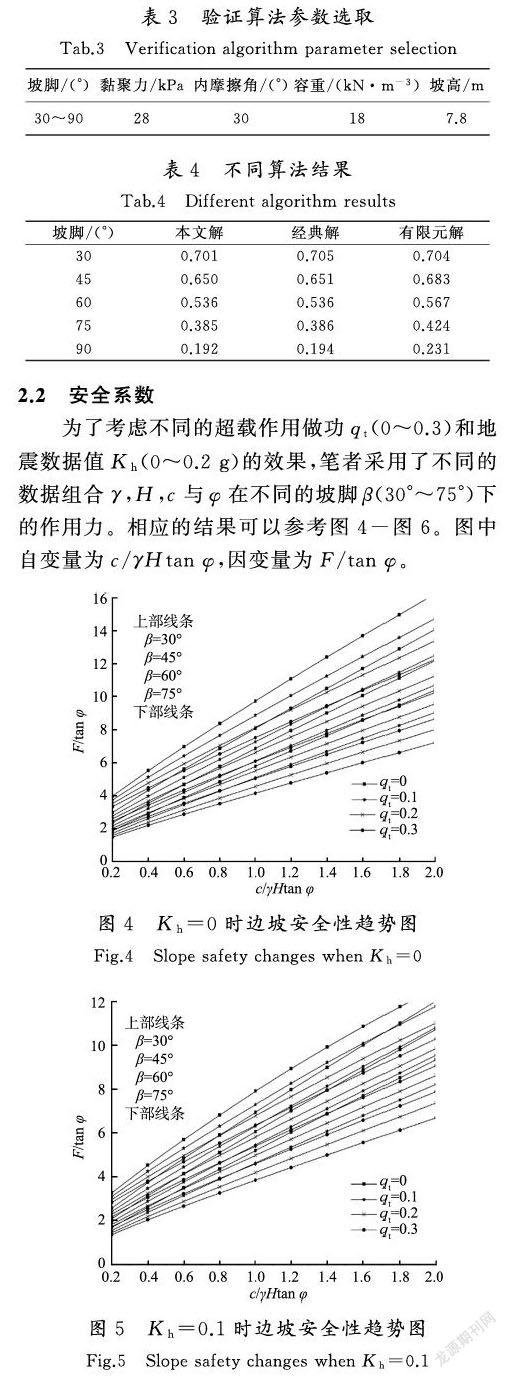
笔者考虑坡顶部的荷载作用，对地震条件下的矿山边坡进行分析，首先通过极限分析法对其临界系数（即临界状态下的安全系数Fs、滑动的临界加速度系数Kc）进行推导，采用Matlab函数进行临界值的搜索验证。以改进的Newmark数值计算法为理论基础，对真实破坏时产生的地震波进行位移计算，详细展示边坡破坏的动态化全过程。

1 超載边坡安全系数及临界加速度的推导

通常采用合适的均质材料分析边坡的安全稳定性。从图1中可以看出：在具有线性关系的强度下，土体的抗剪强度是由内摩擦角和黏聚力共同决定的。而传统的安全系数，在计算时是基于强度折减法的，计算方程式如式（1）所示：

2.2 安全系数

为了考虑不同的超载作用做功qt（0～0.3）和地震数据值Kh（0～0.2 g）的效果，笔者采用了不同的数据组合γ，H，c与φ在不同的坡脚β（30°～75°）下的作用力。相应的结果可以参考图4-图6。图中自变量为c/γHtan φ，因变量为F/tan φ。

在图4-图6中，每张图均被分为4组，坡脚分别为30°，45°，60°，75°，并且4个图例标准为一组，即qt=0，0.1，0，2，0.3，共计16种参数组合。研究发现30°的坡度安全性最大，75°的坡度是具有较大安全隐患的。可以得出结论，上部承重对不同角度的坡度是有安全系数影响的，如果坡脚变大，相应的降幅也变大，最大的降幅数值可达到25%以上，如c/γHtan φ=2，Kh=0.2，β=75°的工况，其安全系数减少25.8%。而地震荷载的作用同样影响显著，如上述相同工况，考虑地震荷载作用后，边坡的安全系数产生了14%的折减。在计算时发现，考虑超载部分的地震动影响，即式（6）的影响结果非常微小，不到1%，故当前研究并没有展示超载部分受地震动的影响。综合考量2种破坏条件（地震力与超载的作用），边坡的稳定性参数降低了40%，例如坡脚为75°，c/γHtan φ=2的边坡，在不考虑任何外力影响时，边坡安全系数组合值Fs/tan φ=10.41，考虑地震力与超载综合作用时安全系数组合值Fs/tan φ=6.19，产生了41%的折减，破坏尤其显著。

2.3 临界加速度

在评估边坡的安全稳定性时，临界加速度系数Kc作为其中的指标，坡度越小，Kc值越小，边坡越容易滑落。通过式（7）计算其临界的加速度，超载部分数值qt=0～0.3，坡脚为30°～90°，内摩擦角为10°～30°，绘制成相应的图表如图7所示，可以发现大部分为破址破坏，而过坡底的破坏机制是水平线区域。当内摩擦角较小时，则对于平缓的边坡，破址破坏下安全系数折减非常显著。然而当考虑水平地震荷载时，对于具有较大内摩擦角的边坡，破址破坏影响显著。对于具有较大参数组合c/γHtan φ值（例如c/γHtan φ=0.2）的陡坡，临界加速度系数Kc随着超载系数的增加而迅速上升。

3 实例位移分析

采用安全系数或临界加速度因素虽然可以有效反映边坡稳定性状态，但其忽略了持续地震作用下的边坡动态破坏的全过程。为了验证算法的有效性，对汶川地震和熊本地震的地震波进行分析，可视化地展示地震发生过程中边坡滑动的全过程，以及各种潜在因素对岩土稳定性的深层影响。笔者对滑落的位移积累过程作出相应解释和计算，拟静力作用下边坡滑落示意图如图8所示。

通过计算分析可以看出，边坡的位移在超载的情况下受到巨大的影响，增加超载作用边坡的累积位移会相应增加。如在图11中，熊本地震边坡的大量位移就是在超载的情况下发生的，3次分别位移了4.72，12.31和26.53 cm，如果没有超载作用，永久位移只有2.37 cm，与最大值相差了11倍左右。而另一个例子针对汶川地震的绵竹清平波，计算得到在考虑超载作用时边坡的永久位移为4.95，11.19和26.84 cm，不考虑超载影响的边坡永久位移为2.15 cm，相差非常显著。

在2种实测地震下，考虑超载的影响会对边坡永久位移产生显著的影响，进一步验证了方法的有效性。因此在高烈度区域进行工程项目的建设时，一定要考虑超载对工程施工的影响，从而避免大规模滑坡灾害发生。

4 结 语

笔者对矿山边坡在地震、超载作用下的滑坡变形进行了分析，采用数值计算法进行了研究，推导了由于地震导致边坡在超载作用下滑坡的临界破坏系数，结论如下。

1）采用的数值算法计算简便，易于求解，结果准确。

2） 上部承重对不同角度的坡度是有安全系数影响的，如果坡脚变大，相应的降幅也变大，最大的降幅数值可到25%以上;考虑地震荷载作用后，边坡的安全系数亦产生了超过10%的折减。综合考量2种破坏条件（地震力与超载的作用），边坡的安全性系数降低超过40%，破坏尤其显著。

3）超载作用下边坡永久位移的影响尤为显著，研究选取了熊本、汶川地震中典型的2条实测波进行分析，结果显示，考虑超载的影响将会对边坡永久位移最大产生数十倍的影响。

当前研究主要基于均质化假设，真实的现场破坏往往基于非饱和边坡状态且土体材料参数呈现非线性特征，后期研究需要考虑诸如土体含水率、地下水位线等参数，使得计算应用范围更广泛。

参考文献/References：

[1] 沈扬，张朋举，闫俊.圆弧滑动法中总应力法和有效应力法适用性辨析[J].河海大学学报（自然科学版），2011，39（5）：517-522.

SHEN Yang，ZHANG Pengju，YAN Jun.Applicability identification of total stress and effeetive stress methods in circular slide analysis[J].Journal of Hohai University（Natural Sciences），2011，39（5）：517-522.

[2] BISHOP A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique，1955，5（1）：7-17.

[3] 周娟，朱峰.中西部地区黏性土质边坡降雨动态渗流的非饱和特性分析[J].河北工业科技，2020，37（4）：273-279.

ZHOU Juan，ZHU Feng.Analysis on unsaturated characteristics of dynamic rainfall seepage of clay soil slope in Central and Western China[J].Hebei Journal of Industrial Scienceand Technology，2020，37（4）：273-279.

[4] 毋遠召，马文礼，魏占玺，等.降雨及渗流条件下层状砂质板岩边坡变形破坏模式研究[J].河北工业科技，2020，37（4）：230-236.

WU Yuanzhao，MA Wenli，WEI Zhanxi，et al.Research on deformation and failure modes of layered sandy slate slopes under rainfall and seepage conditions[J].Hebei Journal of Industrial Scienceand Technology，2020，37（4）：230-236.

[5] 沈珠江.理论土力学[M].北京：中国水利水电出版社，2000.

[6] 董顺德，孙芝玲，何玉鹏，等.气液两相流原理在边坡稳定性分析中的有效性研究[J].河北工业科技，2021，38（1）：25-31.

DONG Shunde，SUN Zhiling，HE Yupeng，et al.Study on effectiveness of gas-liquid two-phase flow principle in slope stability analysis[J].Hebei Journal of Industrial Scienceand Technology，2021，38（1）：25-31.

[7] NEWMARK N M.Effects of earthquakes on dams and embankments[J].Géotechnique，1965，15（2）：139-159.

[8] BRAY J D，RATHJE E M.Earthquake-induced displacements of solid-waste landfills[J].Journal of Geotechnical and Geoenvironmental Engineering，1998，124（3）：242-253.

[9] LIN J S，WHITMAN R V.Decoupling approximation to the evaluation of earthquake-induced plastic slip in earth dams[J].Earthquake Engineering & Structural Dynamics，1983，11（5）：667-678.

[10] RATHJE E M，BRAY J D.Nonlinear coupled seismic sliding analysis of earth structures[J].Journal of Geotechnical and Geoenvironmental Engineering，2000，126（11）：1002-1014.

[11] UTILI S.Investigation by limit analysis on the stability of slopes with cracks[J].Geotechnique，2013，63（2）：140-154.

[12] ZENG Sanpin，LIANG R.Stability analysis of drilled shafts reinforced slope[J].Soils and Foundations，2002，42（2）：93-102.

[13] TANG Gaopeng，ZHAO Lianheng，LIANG Li，et al.Stability design charts for homogeneous slopes under typical conditions based on the double shear strength reduction technique[J].Arabian Journal of Geosciences，2017，10（13）：280.

[14] MICHALOWSKI R L，YOU Liangzi.Displacements of reinforced slopes subjected to seismic loads[J].Journa of Geotechnical and Geoenvironmental，2000，126（8）：685-694.

[15] NADUKURU S，MICHALOWSKI R L.Three-dimensional displacement analysis of slopes subjected to seismic loads[J].Canadian Geotechnical Journal，2013，50（6）：650-661.

[16] CHANG C J，CHEN W F，YAO J T P.Seismic displacements in slopes by limit analysis[J].Journal of Geotechnical Engineering，1984，110（7）：860-874.