Perspective: Acoustic Metamaterials in Future Engineering

Qingbing Lu, Xin Li, Xiujun Zhng, Minghui Lu,b,c,*, Ynfeng Chen,c,*

a National Laboratory of Solid State Microstructures & Department of Materials Science and Engineering, Nanjing University, Nanjing 210093, China

b Jiangsu Key Laboratory of Artificial Functional Materials, Nanjing University, Nanjing 210093, China

c Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China

Keywords:Acoustic metamaterials Sound absorption/isolation Acoustic imaging Engineering application

A B S T R A C T Acoustic metamaterials(AMMs) are a type of artificial materials that make use of appropriate structural designs and exhibit exotic properties not found in natural materials, such as negative effective material parameters (e.g., bulk modulus, mass density, and refractive index). These interesting properties offer novel means for sound manipulation and thus have drawn a great deal of attention. Over the past two decades,tremendous progress has been made in the fundamental research of AMMs,which has not only promoted the development of modern acoustics but also shown the potential of AMMs for engineering applications. Here, we review recent developments in AMMs with a focus on their future engineering,especially in the most promising fields of sound absorption/isolation, acoustic imaging, cloaking, and so on, furthermore, we outline the opportunities and challenges they are encountering.

1. Introduction

Acoustics,a branch of physics concerning the generation,propagation, detection, and conversion of mechanical waves (i.e., sound and elastic waves), is playing an increasingly important role in modern engineering in the fields of communication, ultrasonic imaging, non-invasive high intensity focused ultrasound (HIFU)surgery, and more. In general, the manipulation of acoustic waves has always been a challenge to scientists and engineers because of the strong diffraction and penetration abilities of acoustic waves,which are due to their long wavelength and weak attenuation compared with other types of classical waves [1], despite the fact that strong penetration ability of acoustic waves can be an advantage in some applications,such as ultrasound imaging.With the advent of acoustic metamaterials (AMMs), the manipulation of complex sound and vibrations has become possible. AMMs can be dated back to the 1990s, with the emergence of sonic crystals (SCs)[2,3]. Through the construction of periodic individuals with high impedance contrast to the host matrices, it is possible to create SCs that exhibit unique energy band structures caused by strong Bragg scattering [4,5] of the prorogation waves. Furthermore,negative refraction[6,7], extraordinary transmission [8], and band edge states [9] have been observed in SCs.

With the discovery of metamaterials that have local resonance[10–12],the paradigm of AMMs has been further extended.Unlike SCs,which require the lattice parameters and the regulated wavelength to be on the same order, the lattice constant of local resonant AMMs is much smaller than the wavelength of the target acoustic waves.Thus, local resonant AMMs show potential advantages in the regulation of deep subwavelength waves. For a long time, researchers in diverse disciplines have designed various structures of AMMs with unprecedented constitutive parameters such as negative effective bulk modulus, negative effective mass density, and negative refractive index in order to achieve exotic functions,such as sound absorption[13],cloaking[14,15],focusing[16,17], and a reverse Doppler effect [18]. The related acoustic metasurfaces [19–22], space coiling AMMs [23–25], and miscellaneous AMMs have also greatly enriched the content of AMMs. In addition, inspired by quantum electronics and topological electronics, many AMMs have been designed to analogize these topological phenomena and properties, such as the Dirac-cone type of dispersion relation [26,27], pseudo-diffusion transport [28], topological one-way edge states [29–31], parity-time (PT)-symmetric acoustics [32–34], and non-reciprocal propagation [35,36].

This multifarious research,as mentioned above,has laid a solid foundation for engineering applications in the aviation industry,rail transit, biomedicine, the construction of new infrastructures,and more. However, the challenge of how to design and optimize AMMs to satisfy requirements in the real world remains to be overcome. To date, there are plenty of review articles and books[37–46] on AMMs, which provide a comprehensive and detailed exposition of their physical essence, specific categories of structures,and development context.Here,we will focus on the practical applications of AMMs by reviewing the significant progress that has been made in the fields of sound absorption/isolation,acoustic imaging, cloaking, and so forth. In addition, we will outline the opportunities and challenges of AMMs in future acoustic engineering applications.

2. Applications of acoustic metamaterials

2.1. Sound absorption/isolation

Noise pollution from engines, wheel/rail friction, airconditioners, and so forth, is a major problem impacting human life in society today.Dissipating sound energy and isolating sound propagation are two strategies to reduce or even eliminate noise pollution. However, conventional materials for sound absorption/isolation are bulky [13,47] for low-frequency sound waves, due to their strong penetration and weak attenuation. By enhancing the energy density and employing the bandgap in resonant AMMs,subwavelength structures could efficiently improve sound absorption and block sound propagation, respectively. The vast majority of AMMs for sound absorption/isolation are constructed of decorated membrane resonators (DMRs), Helmholtz resonators (HRs),Fabry–Perot resonators (FPRs), and their miscellaneous variations.

The first DMR metamaterial, which has a circular membrane 0.28 mm thick and a small weight in its center, has achieved a low resonant frequency of 146 Hz [48]. The corresponding wavelength of 2.35 m is much longer than the structural size of the DMRs. Subsequently, thin elastic membranes decorated with designed patterns of rigid platelets [49] (Fig. 1(a)) were demonstrated. To overcome the geometric constraint, which leads to an intrinsic 50%limit for sound absorption[50],three possible strategies were proposed: One strategy is to place the DMRs close to a hard reflecting wall, as the multiple reflections between the wall and the DMRs can result in more than 99% energy absorption[51]. Utilizing the degenerate resonant frequencies of monopolar and dipolar resonators (Fig. 1(b)) is another strategy for perfect sound absorption[52].The third strategy is based on the coherent perfect absorption (CPA) approach, which introduces a control wave in the opposite direction with the same amplitude but opposite phase from the target wave in order to eliminate the reflection and transmission, allowing 100% sound absorption to be realized[53–55]. In addition to noise absorption, DMR metamaterials can be used for noise isolation. Wang et al. [56] proposed a membrane-constrained type of DMR metamaterial that can suppress vibrations at the membrane center to isolate sound transmission at low frequencies. These unique characteristics of DMR metamaterials, along with their simple structure, small volume,and light weight, illustrate the potential applications of these metamaterials in reducing cabin noise in airliners,high-speed railways, automobiles, and ships.

Although DMRs show excellent sound absorption/isolation properties, it is easy for plastic films to fail after functioning for a long time,due to fatigue.Thus,using rigid solid materials to manufacture HRs and FPRs for sound absorption is another research focus. In general, a single HR exhibits monopolar resonances,resulting in a 50%absorption upper bound,due to similar geometric constraints as DMRs. To tackle this problem, Merkel et al. [57]demonstrated a perfect acoustic absorption through the interplay of the inherent losses and transparent modes;in addition, slightly over 50% (and near to 96%) one-sided absorption was achieved in symmetric (and asymmetric) structures. Furthermore, ventilation channels make it possible to absorb sound while maintaining fresh air circulation in a closed environment, such as a concert hall. In addition to the two-port case, an acoustic three-port network based on HRs has been proposed to operate as both a perfect absorber and a coherent perfect transmitter for the same frequency[58].To further reduce the volume,the strategy of embedding apertures based on HRs [59,60] has been introduced.

The above examples confirm that increasing the energy density can greatly improve the sound absorption; however, the narrow bandwidth brought by the resonant features limits the absorption spectrum. A natural idea is to skillfully construct a hybrid system composed of multifrequency resonant units with a slight resonance frequency shift between one another to obtain an overall broad sound absorption spectrum [61–64]. In 2006, a theoretical method based on the radiation impedance of an array panel was proposed [65] to calculate the sound absorption of an HR array in a low-frequency range. Since then, this kind of narrow-neck HR has been widely explored to reduce the resonator’s spatial scale and realize broadband sound absorption. One example is to insert one or more separate plates with small holes into the interior of an HR,leading to a perforated composite HR[66](Fig.1(c)),which can achieve continuous near-perfect absorption in a broadband range of 450–1360 Hz.

For FPRs, each channel requires one-quarter of a wavelength,which is a significant scale for absorption structures in the lowfrequency range. Coiling or folding the channel is one efficient way to reduce the size of the absorbers. By stacking the channels together with various resonant frequencies, the coiled-up space structures [23,67,68] show good sound absorption performance in a broad bandwidth. However, the question of whether there exists a minimum thickness for an absorber with a given sound absorption performance over a designated frequency range remained unresolved until the discovery of the causality constraint[13,69], which revealed a tradeoff between minimizing the absorber’s thickness and broadening its absorption spectrum.Under the guidance of the causality constraint, Yang et al. [69] realized a 10.86 cm-thick structure exhibiting a broadband, near-perfect flat absorption spectrum (Fig. 1(d)). In some cases, however, the causality constraint can be circumvented by manipulating the boundary condition on the backside of the absorber. Mak et al.[70] realized a minimum absorber thickness that was an order of magnitude less than the causal limit. Recently, based on the Fano-like interference, a planar acoustic ventilation barrier with a central hollow orifice and two surrounding helical pathways of varying pitch was proposed [71], which can block more than 90% of incident energy in the frequency range of 900–1418 Hz(Fig.1(e)).Compared with DMR-type AMMs,HR and FPR metamaterials composed of rigid solid materials can greatly prolong the service life. Given their load-bearing and decorative functions,these AMMs hold promise for noise reduction in application such as expressways, smart power grids, and high-speed trains.

Waterborne sound absorption/isolation using AMMs is another direction for the potential application of AMMs in the fields of sonar shielding, underwater communication, ocean development,and so forth. However, research on waterborne sound absorption/isolation metamaterials progresses slowly because the high hydrostatic pressure and moderate impedance contrast hinder the construction of ‘‘meta-atoms.” Some preliminary attempts have been based on embedded bubble structures [72–74] or high-density spheres coated by a viscoelastic matrix as resonant units[75].One example involves AMMs based on patterned bubble arrays in water [76], which are inspired by biological superhydrophobic systems.This type of AMM can block sounds at low frequencies because of local resonances. By varying the sizes of the bubbles and the distance between them without changing the thickness,the operating frequency can be tuned in the range of 9–1756 kHz. Duan et al. [77] reported another kind of lightweight AMM constructed of a rubber coating and an embedded metallic neck into the classical Helmholtz resonant cavity. With tailored internal geometric parameters, this type of quasi-Helmholtz resonator achieved almost perfect absorption from 306 to 921 Hz.To broaden the bandwidth of the sound absorption,Zhang et al.[78]recently proposed a method to use varied scatterer sizes(Fig. 1(f)), and Shi et al. [79] used multiple coating layers.

Fig.1. AMMs for sound absorption/isolation.(a)Sample photograph of a dark AMM.(b)Schematic cutoff view of degenerate resonators.(c)View of a three-port network of HRs. (d) Schematic of perforated composite HRs. (e) Schematic of two spiral helices with a central orifice. (f) Schematic diagram of an absorber consisting of a viscoelastic coating layer embedded with periodically distributed plate scatterers. (a) Reproduced from Ref. [49] with permission; (b) reproduced from Ref. [52] with permission;(c)reproduced from Ref.[66]with permission;(d)reproduced from Ref.[69]with permission;(e)reproduced from Ref.[71] with permission;(f)reproduced from Ref.[78]with permission. The defination of all the abbreviations in figures could be find in the cited references.

In addition to resonant structures, non-resonant metamaterials with a gradient index utilize the density change of the scatterers to modulate the local refractive index,so as to control the loss of incident sound waves. Based on the acoustic black hole principle and multiple scattering theory, Naify et al. [80] designed a cylindrical shell with a linearly graded sound velocity for omnidirectional underwater sound absorption. On this basis, Wang et al. [81]further developed a new two-dimensional (2D) axisymmetric underwater omnidirectional absorber with an acoustic gradient index structure and a hollow absorbing core. Nevertheless, the demonstration of megahertz ultrasonic waves corresponding to small wavelengths still presents difficulties for the processing and preparation of AMMs (see Section 3 for more detail).

2.2. Acoustic imaging

Acoustic imaging has important applications in medical ultrasound, nondestructive testing, and photoacoustic imaging. Pursuing high resolution has always been an important task in these fields.As with optical imaging,evanescent waves carry the detailed information of an object and exponentially decay as they leave the object’s surface. As a result, conventional optical/acoustic imaging techniques often fail to collect the information from evanescent waves; therefore, the imaging resolution is strictly constrained by the diffraction limit. How to obtain the information carried by evanescent waves is the key to realizing high-resolution imaging.Based on AMMs, two main strategies have been proposed. One relies on amplifying the evanescent waves for detection within a certain distance[82],and the other converts evanescent waves into propagating waves [83] for convenient measurements.

The first strategy is inspired by Pendry’s [84] ‘‘perfect lens,”which can strongly amplify optical evanescent waves by using negative refractive index materials [85,86]. In acoustics, a 2D membrane-based metamaterial has been designed that exhibits a negative refractive index.Using this AMM,a 17-fold net amplitude gain from an evanescent wave source has been achieved[78].Similar designs have also been proposed for acoustic surface waves,where the smaller wavelength (compared with bulky acoustic waves)imposes challenges for imaging restricted by the diffraction limit[87].It has been shown that,by using a 2D membrane-based metamaterial, the surface evanescent waves can be amplified and two-point sources with a distance of 1/17 wavelength can be resolved [88] (Fig. 2(a)). Beyond types of membrane, Kaina et al.[89] proposed a negative refractive index acoustic superlens composed of HRs (Fig. 2(b)), where subwavelength focusing seven times greater and a resolution 3.5 times better than the diffraction limit have been achieved.

The second strategy is based on anisotropic metamaterials that can convert evanescent waves into propagating waves due to their ability to couple large wave vector components (i.e., evanescent components). In general, the realization of this type of AMM is based on exciting trapped resonances inside acoustic waveguides[83,90,91]. By converting evanescent waves into propagating waves,anisotropic AMMs can realize high-resolution imaging even at the far field. For example, Li et al. [83] used 36 computernumerical-controlled brass fins to convert evanescent wave components into propagating waves that can travel to the far field,where the associated deep subwavelength features remain intact(Fig. 2(c)).

In addition to the above-discussed strategies, by exciting waveguide resonances in a slab with a high-index contrast to its surrounding medium, the high spatial components of the subwavelength details can couple to the trapped modes of such a slab waveguide, and a subwavelength image can be obtained at a distant plane[92].Super-oscillation acoustic wave packets generated by an ultrasonic metalens provide another means of breaking the diffraction limit for ultrasound imaging [93] (Fig. 2(d)). In regard to the narrow working bandwidth of AMMs,which can lead to serious chromatic aberration in imaging,some non-resonant elements[83] and a fin-shaped hyperlens [94–96] have been proposed to address this problem.

While most imaging applications of AMMs focus on airborne sound, some proposals on underwater acoustic lenses have begun to emerge [97,98]. For example, Peng et al. [99] designed gradient negative refractive index metamaterials to realize broadband underwater acoustic focusing, whose focal distance can be tuned by changing the lattice distance. These metamaterials can potentially be used in ultrasonic imaging, which is commonly based on the pulse-echo process that requires a broad bandwidth for focusing.Other methods to realize a broadband focusing lens with a gradient index involve utilizing 2D pentamode materials [100], using metasurfaces with non-resonant arrangements [101], or even using simple SCs made of single-phase rods, where an acoustic composite lens is realized to perform three-dimensional (3D)underwater focusing at a frequency range between 15 and 25 kHz [102] (Fig. 2(e)).

2.3. Other applications

In addition to the applications discussed above, there are several other noteworthy branches such as cloaking, unidirectional propagation, acoustic complementary metamaterials, and impedance matching. Cloaking, which was first proposed in optics[103,104], describes a phenomenon in which an object is invisible to incoming detection as if it disappears. This interesting phenomenon and its related subjects,such as illusion,have important applications in the fields of target stealth and security. Based on the transformation acoustic equations [105–107], various structures have been proposed for cloaking,such as alternating isotropic layers [108], multilayered composites [15], and pyramid-like perforated plate structures [109,110]. For underwater acoustic cloaking, Zhang et al. [111] proposed an AMM constructed with a planar network of subwavelength cavities connected by narrow channels (Fig. 3(a)).

Unidirectional sound propagation, in which the incident wave propagates only in one direction and is blocked in the other direction, behaves like a diode and can potentially be used for communication, anti-eavesdropping, and acoustic calculation. For such a non-reciprocal propagation, it is usually necessary to break the time-reversal symmetry by introducing a circulating fluid [36],which often leads to new problems such as instability and high viscosity. Another solution is based on breaking the spatial inversion symmetry, which gives rise to unidirectional sound propagation with higher efficiency,broader bandwidth,and much lower power consumption [112] (Fig. 3(b)).

To realize unidirectional propagation or to reduce backscattering, another flourishing field has recently attracted a great deal of attention—namely, the topological phases of matter [113,114].Originating in electronic systems and firstly found to be responsible for the famous integer quantum Hall effect,topological physics was soon extended into the classical realms of optics[115,116]and acoustics [117,118], where metamaterials serve as resourceful material platforms to greatly enrich and simultaneously benefit from studies of the topological phases of matter. Due to their nature of topological protection, topological materials support robust interface states that are immune to backscattering [117]. This feature enables revolutionary applications in various fields, including low-loss waveguides, topological filtering, and collimations. More interestingly, topological phases of matter bring new degrees of freedom to light and sound control. For example, by designing a 2D honeycomb lattice composed of steel rods, He et al. [119]realized the acoustic analog of the quantum spin Hall effect, which supports backscattering-immune sound transportation (Fig. 3(c)).The creation of pseudospins in acoustics opens up the field of acoustic spintronics[22,120],which may have interesting applications in acoustic communications and spin-dependent information processing. In addition, recent developments in acoustic valley insulators [121], Weyl semi-metals [122], and higher-order topological insulators [31] has further inspired various methods for sound control, in addition to versatile applications.

Moreover,when sound waves encounter obstacles or interfaces with a large impedance mismatch, a considerable amount of acoustic energy will be scattered. To restore the distorted acoustic fields, acoustic complementary metamaterials (CMMs) have been proposed. In general, CMMs simultaneously require negative and anisotropic material properties in order to prevent large resonant damping. They have potential applications in transcranial ultrasound and nondestructive testing, where sound waves often encounter aberrating layers such as skulls, steel plates, and layers with a large impedance mismatch.For example,a quasi-2D acoustic CMM utilizing clamped membranes and side branches[123]has been proposed to restore the diffraction from an aberrating layer in a noninvasive manner (Fig. 3(d)).

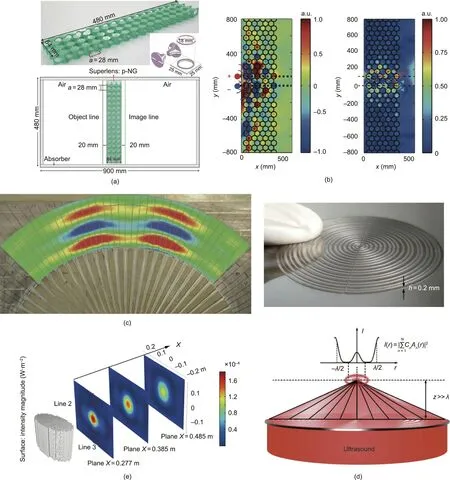
Fig. 2. AMMs for imaging. (a) Superlensing slab made of a membrane-based AMM. (b) Super-resolution imaging for two sources out of phase by using a flat acoustic superlens.(c)Experimental demonstration of the magnifying imaging of a sub-diffraction-limited dual-source.(d)Photograph of an ultrasonic metalens(upper panel)and a super-oscillating field pattern beyond the evanescent region(lower panel).(e)Numerical results of the wave intensity for an approximate plane wave.(a)Reproduced from Ref. [88] with permission; (b) reproduced from Ref. [89] with permission; (c) reproduced from Ref. [83] with permission; (d) reproduced from Ref. [93] with permission;(e) reproduced from Ref. [102] with permission. The defination of all the abbreviations in figures could be find in the cited references.

Overcoming the large impedance mismatch and enhancing sound transmission at the water–air interface hold great significance for underwater communication, imaging, and remote sensing. Acoustic metasurfaces have been demonstrated to be able to break through the limitation of quarter-wave plates or multilayered antireflection coatings for impedance matching[124].A metasurface consisting of a locked air layer and a hydrophobic solid substrate with multiple hollow cells has been proposed to enhance the energy transmission by over 200 times at the frequency range of 10–4000 Hz[125].By changing the immersion depth of the solid substrate, the working frequency can be tuned while maintaining the energy transmission. Inspired by the ‘‘lotus effect,” a microscale air layer is constructed using a superhydrophobic aluminum plate and water [126]. A nearly 100% energy transmission coefficient and a wide-angle water-to-air acoustic transmission can be obtained in the frequency range of 10–100 kHz.

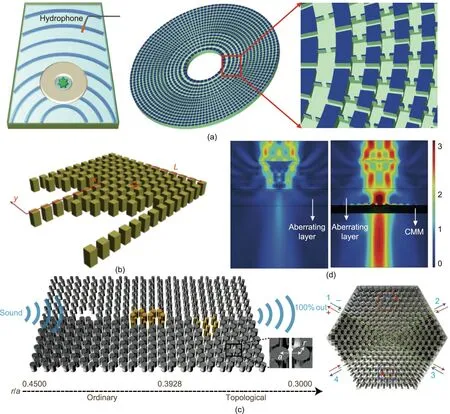
Fig.3. (a)Schematic diagram of acoustic cloaking and the configuration of an acoustic cylindrical cloak.(b)Schematic diagram of a sonic-crystal-based acoustic diode with a periodic arrangement in the y-direction.(c)Schematic of an acoustic topological insulator constructed with two types of phononic‘‘graphene”with the same lattice constant but different‘‘atom”(i.e.,stainless-steel rod)radii(left)and a photo of the cross-waveguide splitter(right).(d)Acoustic intensity fields of an unfocused beam in a skull only(left) and with CMM and the skull (right). (a) Reproduced from Ref. [111] with permission; (b) reproduced from Ref. [112] with permission; (c) reproduced from Ref. [119]with permission; (d) reproduced from Ref. [123] with permission. The defination of all the abbreviations in figures could be find in the cited references.

Another application is in medical ultrasound, which requires impedance matching between piezoelectric materials and human body tissues. Introducing an AMM layer with a gradient index is a common means of achieving impedance matching [127]. Li et al. [128] proposed an anisotropic cone-structured AMM matching layer with a gradient acoustic impedance along the ultrasound propagation direction to realize the extraordinary transmission of ultrasound over a wide frequency range. In the abovementioned studies,the impedance-matching effect is efficient for normal incidence but gradually deteriorates when the incident angle increases. To achieve wide-angle acoustic impedance matching,Liu et al. [129] used silicone rubber to design one-dimensional(1D) and 2D acoustic structures by applying the effective medium theory with spatially dispersive parameters. In this way,wide-angle and broadband impedance matching with water was realized, leading to near 100% transmission of acoustic waves in water.

3. Discussion

In this perspective, we first briefly provided a panorama of AMMs to establish a framework for this topic. We then reviewed the potential applications of AMMs in several promising fields,such as sound absorption/isolation, imaging, acoustics, and cloaking. Despite the great success of fundamental research on AMMs, AMMs still present several challenges in practical engineering.

The narrow working bandwidth induced by resonances and the inevitable energy loss resulting in low transmission coefficients can substantially impede the practical application of AMMs. The two main solutions for the former issue are integrating AMMs with a broad resonant spectrum and designing tunable active metamaterials.As a possible solution for the latter issue, the recent development of topological insulators and associated topological devices provides robust lossless acoustic propagation, thanks to their topological protection.In addition,loudspeakers,transducers,and other energy-conversion methods(e.g.,multi-physics coupling with temperature or electromagnetic regulations)can be employed to compensate for the energy dissipation of AMMs. Other explorations of, for example, the physics of non-Hermiticity and the parity-time symmetric properties of AMMs may reveal even more novel and interesting ways to manipulate acoustic waves and facilitate their application accordingly.

Aside from airborne AMMs, growing attention is being paid to the design of metamaterials used in fluids such as water or in human tissues. However, as discussed above, the impedance contrast between fluids and solid AMMs is relatively small(only about one order of magnitude).A considerable amount of acoustic energy transmitting into both fluids and solid structures could result in a complex travel path and therefore limit the obtainable effective acoustic parameters. One strategy that might address this challenge is to build air bubbles as resonators or to wrap air with elastic film bubbles; in such contexts, the effective parameters can be modulated by varying the preset pressure of the bubbles or by choosing different wrapping materials.

Another challenge lies in the manufacturing of AMMs. Simplestructure AMMs [130,131] can be fabricated by means of conventional fabrication approaches, including machining, casting, injection molding, and laser cutting. AMMs with complicated 3D structures, such as channels [67], chambers [132], and spherical or cylindrical fillers [10], mainly rely on manual manufacturing and 3D printing. However, massive manual manufacturing potentially leads to a loss of consistency and unstable product quality.3D printing technology is well-suited to manufacture complicated structures.Nevertheless,when it comes to massive production,3D printing may suffer from high-cost consumption, low production efficiency, and limited varieties of materials. Therefore, on the route to real-world AMM applications, it is particularly urgent to develop a new generation of 3D printing technology with low cost,high efficiency, and various materials. Furthermore, AMMs in the megahertz range are of great value for improving the resolution of medical ultrasonic imaging and the focusing of high-precision noninvasive surgeries. However, manufacturing methods at the micron scale are rarely reported.Thus, advanced micro/nanofabrication is urgently demanded in the preparation of high-frequency metamaterials.

In addition,emerging ideas on controlling sound fields globally and tailoring AMMs for expected functions and properties have become essential for the use of AMMs in practical engineering,which must be compatible with existing acoustic devices. However, determining the complex relationship between the structures, functions, and properties of AMMs requires considerable effort. Digitizing AMMs in combination with artificial intelligence is the most likely path to save time and effort on non-innovative designing. As shown in Fig. 4, an overall consideration of fundamentals, performance, fabrication, and application in the design and optimization of exquisite AMMs that are balanced in all aspects is the key to ultimate industrial applications.

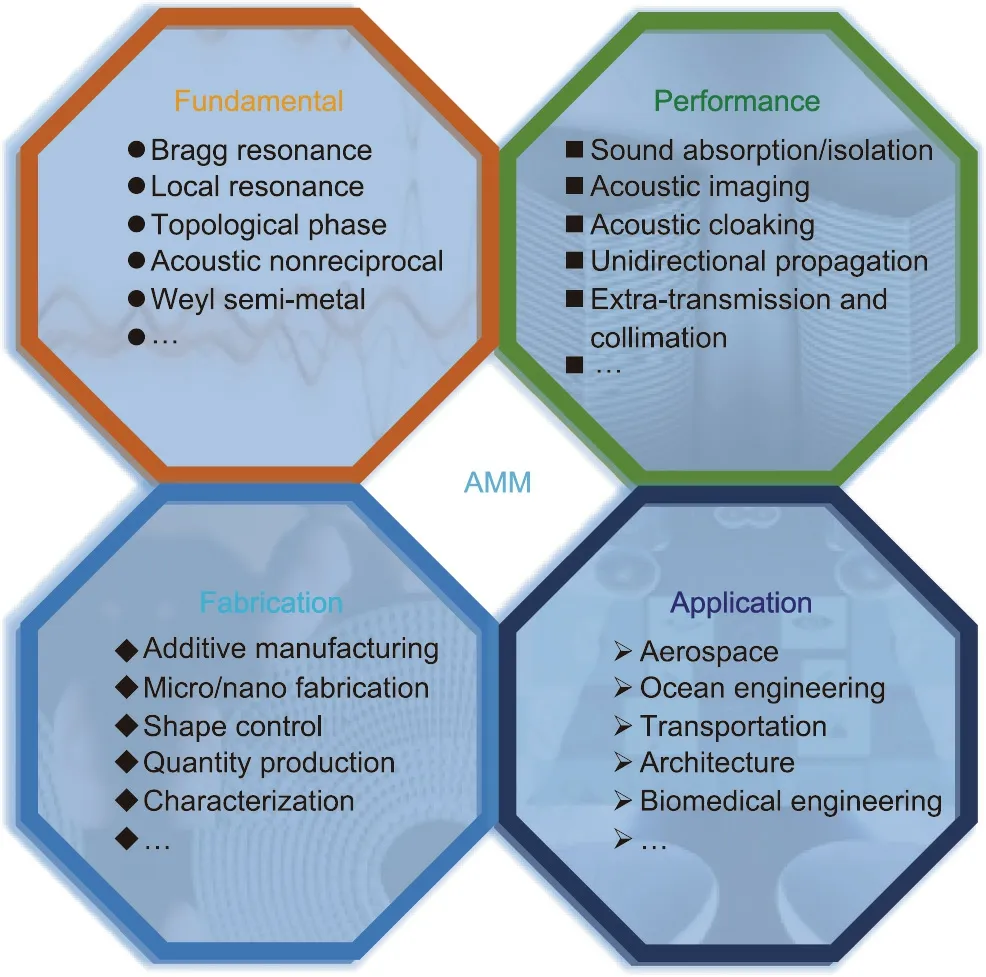
Fig.4. Factors should be comprehensively considered in the design and preparation of AMMs.

Acknowledgments

This work is supported by the National Key Research and Development Program of China (2017YFA0303702 and 2018YFA200) and the National Natural Science Foundation of China (12172164, 11625418, 11774297, 51732006, 11890700,and 51721001).

Compliance with ethics guidelines

Qiangbing Lu, Xin Li, Xiujuan Zhang, Minghui Lu, and Yanfeng Chen declare that they have no conflict of interest or financial conflicts to disclose.