一种双端固支微梁结构⁃静电耦合分析及仿真

刘 恒，孙亚坤

（南京信息工程大学 电子与信息工程学院，江苏 南京 210044）

0 引言

对于微机电系统中静电驱动的微构件，在电场力作用下，微结构发生变形，结构的变形又导致了电场力的改变，从而形成了结构⁃静电场耦合问题。微机电系统的设计水平和产品的可靠性与正确分析和求解静电力驱动的微结构变形、临界（pull in）电压等参数有关。对于机电耦合问题，一般采用悬臂梁或双端固支梁结构作为研究对象。将结构简化为“弹簧⁃质量”模型是耦合分析的一种，但是对于建立的方程，由于边界条件和器件的结构过于复杂而往往难以获得精确的解析解。因此机电耦合问题的建模和分析过程中更多的是借助于数值计算软件进行多能量场耦合分析，然后确定优化结果，例如有限差分法（FD）、边界元法（BEM）、有限元法（FEM）等。其中有限元法和边界元法能够获得较为精确的物理级分析计算结果，利用综合法可以获得结构在每个能量域内行为的精确描述，但对于结构设计来说，这种计算方法效率低，过程复杂，且不适合系统级的分析计算，不能同时考虑电路和结构器件的设计，实现上述分析需要减少系统模型参数，即集总模型或降阶模型。集总参数模型是强耦合模型，具有求解收敛速度快的优点，应用范围非常广。本文以双端固支梁为研究对象，建立其结构⁃静电耦合方程，推导出临界驱动电压的近似解。利用有限元分析软件进行仿真，验证了解析解的有效性，并提出一种基于集总参数模型求解临界电压的方法，仿真结果与有限元分析相近，但大大减少了计算时间，并且有利于快速地分析与设计机械结构和驱动电路。

1 静电驱动的双端固支梁建模

双端固支微梁系统结构模型如图1 所示。

图1 静电驱动下的双端固支梁模型

在电压的作用下，固支梁由于静电力的作用产生变形，静电力为：

式中：，分别为电极的宽度和梁的长度；为电极和梁的初始间距；为梁的宽度，电极宽度大于梁的宽度；为介电常数；为加在电极和梁上的电压；为静电力。在梁的中点处纵向位移最大，满足如下条件：

当电极的宽度远小于梁的长度时，式（1）近似化简为：

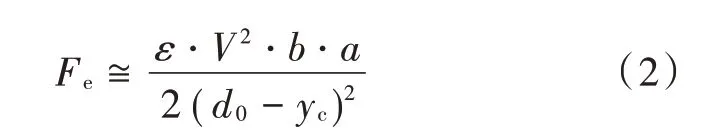
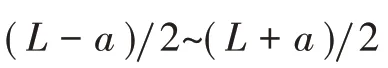
根据式（4）、式（6），结合边界条件可得：

得到：

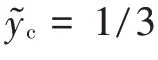
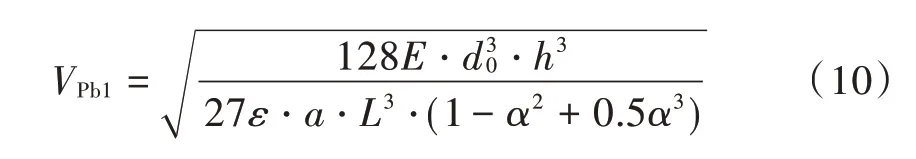
该解析过程由于在式（8）中采用了近似减少极板间距的方法，解析结果必然小于实际精确的临界电压。

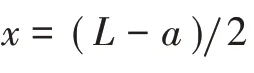
当式（1）中的()接近y时，静电力为：

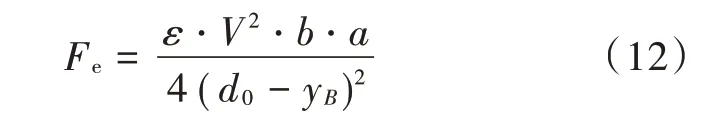
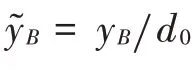
相应的临界电压为：

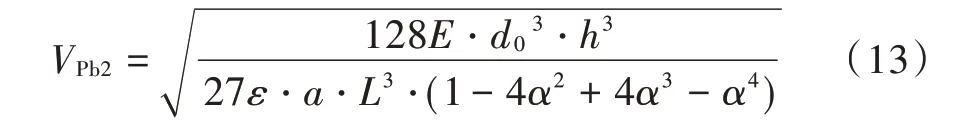
式（13）是临界电压的上限，当较小时，式（10）和式（13）非常接近。

2 有限元方法和集总参数模型的应用

本文采用混合有限元方法结合边界元方法来求解双端固支微梁在静电力左右下的结构⁃静电耦合问题。将能量场分为力场和静电场，用不同的控制方程来描述力场和电场中的能量。在进行离散化时，两个能量场中的节点定义独立的节点自由度，根据力的边界条件和位移协调边界条件将它们结合起来。在结构表面的电场分布采用边界元方法，而结构的变形则采用有限元法。这样做一方面可有效地利用FEM 易于求解结构变形的优点，另一方面可以很容易用BEM 调整电场的构型，直接得到需要的结构边界电场，节省大量的计算资源。

双端固支梁结构参数的选取来自文献[13]，如表1所示。在Coventor 软件下基于计算机虚拟微加工工艺建立梁和电极的实体模型，如图2 所示。在分析中，固定梁的两个侧面均为导体。在电极上所加电压为0 V，在梁上加正向电压。

表1 结构几何尺寸

图2 有限元分析的实体模型

临界下拉电压分析参数设置为：驱动电压扫描范围为20～50 V，收敛电压容许差值为0.5 V。利用软件自带的耦合场分析器，得到的迭代过程如图3 所示。临界下拉电压为42.187 5 V。电极长度和梁长度相等，等于1，解析计算结果为35.368 2 V，文献[13]计算的结果为39.5 V。

图3 临界电压有限元分析过程

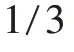
图4 不同驱动电压下梁的纵向位移

基于有限元和边界元的数值计算仿真方法虽然可以较精确地得到耦合的临界下拉电压，但需要的时间较长，本文为了减少计算机运行时间，单元网格划分得比较粗糙。这就是本文的有限元分析结果与文献[13]结果不一致的原因。对于不同的梁和电极结构几何参数，要不断的重新设计二维版图尺寸，然后相应的三维模型实体才可以得到调整。分析、设计效率非常低，特别是复杂微机电系统。鉴于此，本文利用集总参数模型来分析固支梁的下拉临界电压。其中虚拟的工艺文件中固支梁为结构层，厚度为3 μm，电极层厚度也为3 μm，中间牺牲层厚度为1 μm，尺寸与表1 相一致。梁中点处沿轴方向的位移通过自由度转换模块以数值的方式表示，模块是基于MAST 语言的宏模型。梁和电极的几何尺寸参数通过全局变量来设置，改变全局变量的值就自动改变二维版图，结合虚拟的工艺就可以得到三维实体结构，分析、设计效率得到提高。整个分析用的集总参数模型如图5 所示，模型包括电极梁（Electrode beam）、临界电压源（Pull⁃in Resource）、锚点（Anchor）、全局变量（Coventor）等宏模型，梁两端的锚点固定在圆片的底座上。对应的二维版图如图6 所示。改变全局参数就可以方便快捷地得到不同尺寸的版图。

图5 基于集总参数临界电压分析模型

图6 基于集总参数分析模型对应版图

对集总参数模型进行时域分析，在Saber 仿真中，接近临界下拉电压时出现奇点，仿真停止。驱动电压和纵向位移数据经Matlab/Simulink 中SaberSimulinkCosim 接口得到驱动电压和梁在轴的曲线，如图7 所示。

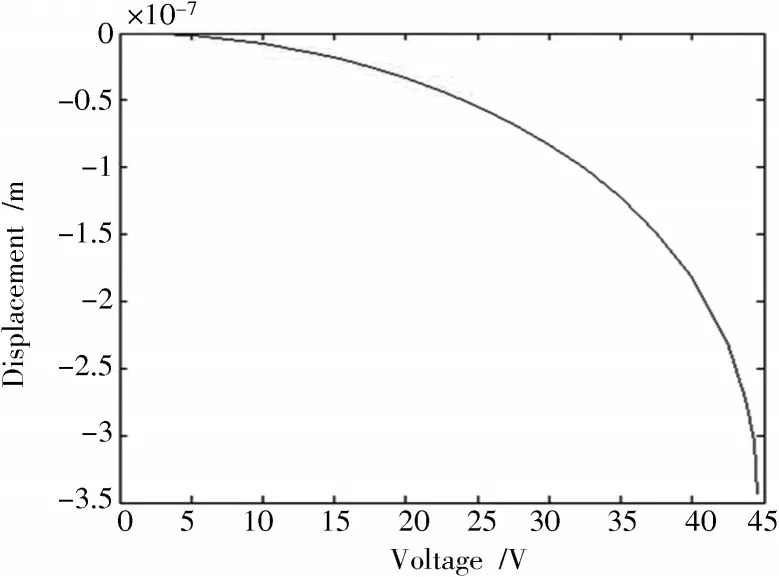
图7 基于集总参数模型的临界下拉电压

从图7 可知，临界下拉电压为44.531 2 V，在接近临界下拉电压时，曲线变化幅度趋于无穷，仿真产生奇点。仿真结果与文献[13]介绍的结果有一定误差，但仿真过程不需要重复划分网格，可以进行后续外围电路分析，提高了微机电系统的设计效率。

3 结论

对于复杂的微构件的结构⁃静电耦合场分析，一般很难建立耦合动力学方程；即使建立了方程也很难得到精确的解析解。基于有限元和边界元的计算机软件仿真虽然能获得较精确的数值解，但是需要不断地划分单元网格，重复计算，效率非常低。基于MAST 语言的集总参数模型的力电耦合分析方法不需要划分网格，能较快速地求解耦合问题。本文以双端固支微梁为例，利用三种不同方法分析结构⁃静电耦合场，为求解复杂微机电系统中多能量场耦合问题提供依据，从而提高设计产品的可靠性。