装配式波纹钢板综合管廊连接节点抗震性能分析

廖 凯， AUNG Khaing Min， 岳 峰, *， 刘博文， 熊石根， 江孝礼

(1. 上海交通大学船舶海洋与建筑工程学院土木工程系， 上海 200240； 2. 上海市公共建筑和基础设施数字化运维重点实验室， 上海 200240；3. 海洋工程国家重点实验室， 上海 200240； 4. 利兹大学土木工程学院， 英国 利兹 LS2 9JT；5. 湖南金迪波纹管业有限公司， 湖南 长沙 410114)

0 引言

城市地下综合管廊是浅埋于城市道路下方的公用隧道空间，是将电力、通信、燃气、给排水等管线集中敷设的构筑物，被称作“生命线工程”[1]。近年来，随着我国城镇化水平逐步提高，从中央到地方都在积极推进城市地下综合管廊建设。自2021年开始，各地相继出台的“十四五规划”均明确提出城市地下综合管廊建设规划，城市地下综合管廊的建设将迎来前所未有的高峰期。我国现阶段地下综合管廊大多使用钢筋混凝土结构。混凝土管廊耐久性和耐火性良好，但刚度较大，导致抗震性能薄弱，且易发生不均匀沉降，在外力作用下易发生折断。波纹钢管廊具有强度高、力学性能稳定、自重轻、运输便捷、施工周期短和回收利用率高等优点;同时,波纹钢结构属于柔性结构，不仅在横截面内与土体变形相适应,且在纵向上能抵抗基础不均匀沉降；当埋深达到一定程度时，回填土与波纹钢管廊形成土拱效应共同承载，降低了用钢量；因此，波纹钢管廊具有钢筋混凝土管廊不可比拟的优势。

在波纹钢板节点静力性能研究方面： Sim等[2]探讨了板厚对钢波纹板抗压强度的影响；Kim等[3]建立了波纹钢涵洞精细化有限元模型，研究了螺栓接缝强度与板厚之间的关系；刘天正等[4]通过纯弯试验研究了法兰板厚对波纹钢板法兰连接节点承载力的影响；苏明周等[5-6]、赵凯[7]通过开展试验研究与数值模拟分析，探讨了螺栓预紧力、端距，波形、板厚、材料等因素对高强螺栓连接波纹钢管廊纵向接缝处的承载力的影响。在波纹钢管廊抗震性能研究方面： 岳峰等[8-11]采用缩尺模型对预制装配式钢波纹管综合管廊开展不同场地条件下的大型振动台试验研究，提出了影响管廊动力响应的关键因素；同时，建立了有限元模型，通过参数分析探讨了管廊结构与周围土体之间的相互作用机制，并提出了考虑土-钢相互作用的波纹钢管廊抗震计算方法。

拟静力试验是目前结构抗震领域中采用最广泛、最成熟的研究方法之一，尤其适用于研究构件与节点的抗震性能。由于地下结构受周围土体约束，与地上结构有较大不同，拟静力试验方法很少应用于地下结构抗震性能研究。刘晶波等[12-13]提出了一种适用于地下结构抗震性能研究的Pushover分析方法，并验证了其精确性与适用性；孔令俊[14]在验证对地下结构开展拟静力试验的可行性后，通过拟静力试验及数值模拟对混凝土箱涵结构的抗震性能进行了研究；Watanabe等[15]对钢筋混凝土箱涵节点开展了拟静力试验研究，并提出了确定开裂强度和屈服强度的方法；魏奇科等[16]对叠合装配式钢筋混凝土地下综合管廊边节点与中节点开展了拟静力试验研究，分析了试件的滞回性能；冯丹[17]对使用套筒灌浆连接技术完成的装配式综合管廊节点进行了拟静力试验研究，对比分析了不同连接方式下综合管廊的滞回性能；杨艳敏等[18]对叠合装配式钢筋混凝土综合管廊开展了拟静力试验研究，探讨了覆土高度、施工工艺、腋角高度等参数对结构抗震性能的影响；李正英等[19]对设置镦锚钢筋的钢筋混凝土综合管廊节点进行了拟静力试验与有限元模拟，探讨了锚固长度对节点抗震性能的影响。

从目前国内外综合管廊相关研究来看，学者们针对钢波纹管的静力学性能研究相对较多，且多集中在内部空间利用率较低的圆形截面；对于管廊抗震性能的研究集中在混凝土结构上，而对波纹钢管廊抗震性能的研究相对较少，节点连接部位的抗震研究更鲜见报道。波纹钢管廊是装配式结构，节点部位在地震作用下起到关键性控制作用。因此，本文基于一个管片间采用法兰连接的实际工程，建立矩形截面波纹钢板管廊节点精细化有限元模型，通过数值模拟计算，研究法兰连接的力学行为和抗震性能，探讨法兰厚度、管廊壁厚、螺栓位置等参数对结构抗震性能的影响，并找出控制管廊抗震性能的关键参数。

1 有限元模型建立与验证

1.1 模型尺寸设计

以山西平遥古城基础设施提升项目波纹钢板综合管廊工程为依托，选取与工程实际相同尺寸的波纹钢板管廊进行精细化建模分析。如图1所示，管廊截面为内部空间利用率较高的圆角矩形，净尺寸为1.6 m×2.7 m，波纹钢板厚度为6 mm。钢板宽度(节段长度)为1.2 m，波纹钢板波形为200 mm×55 mm，波谷半径R为53 mm，如图2所示。为保证波纹钢板管廊的强度及刚度，减小接缝强度衰减，波纹钢板管上的搭接缝以最少为原则，环向采用4片板(A、B板各2片)拼装，如图3所示。板片间采用法兰连接，法兰均焊接在波纹钢板上，法兰板厚为9 mm，连接螺栓采用10.9级的高强M20螺栓，同时为方便安装，法兰上螺栓孔直径取25 mm，如图4所示。

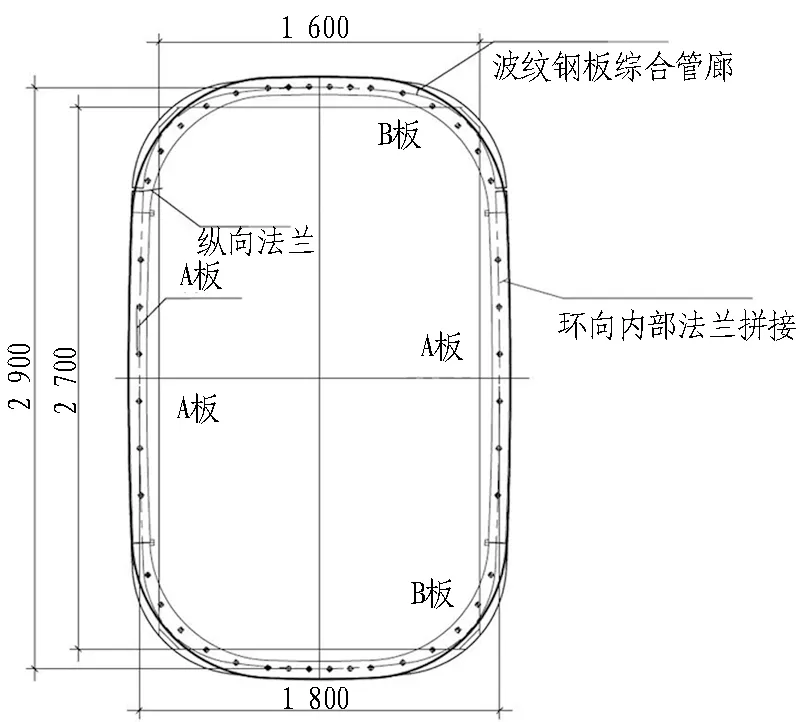
图1 波纹钢板综合管廊标准断面图(单位： mm)Fig. 1 Standard section of corrugated steel plate utility tunnel (unit: mm)

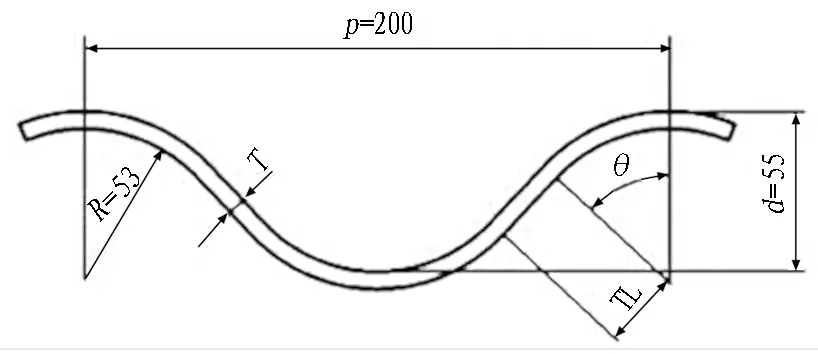
图2 波纹示意图(单位： mm)Fig. 2 Schematic of corrugation (unit: mm)

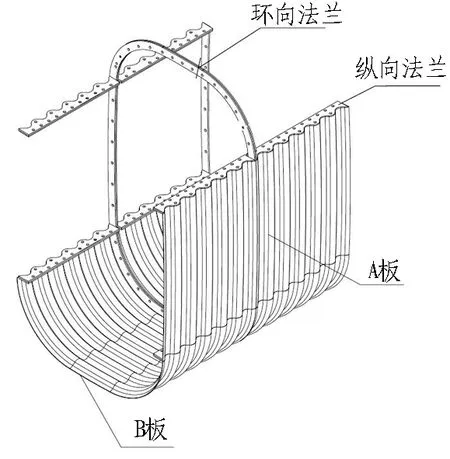
图3 管廊板片示意图Fig. 3 Schematic of corrugated plates

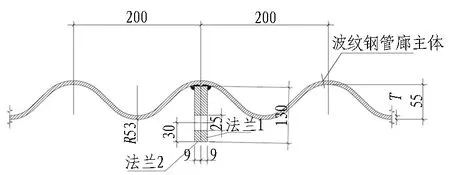
(a) 环向法兰连接大样图

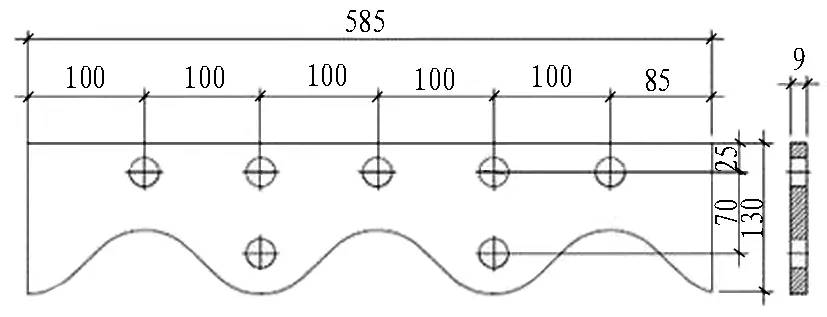
(b) 纵向法兰详图图4 法兰细部构造(单位： mm)Fig. 4 Detail structure of flange (unit: mm)

本次试验选取两端管廊中部拼接段进行拟静力试验，如图5所示。选取管廊壁板下部节点进行试验分析，如图6所示。

图5 综合管廊选段示意图 Fig. 5 Diagram of section selection of utility tunnel

图6 试件位置示意图 Fig. 6 Diagram of specimen position

1.2 参数选取

对于钢材的常规弹性分析，大多数模拟采用理想弹塑性模型，但本文试件处于低周往复荷载受力条件下，因而数值模拟中钢材本构关系选用线性强化弹塑性模型，其表达式见式(1)，模型示意见图7。

图7 钢材本构模型Fig. 7 Steel constitutive model

(1)

式中：E为钢材弹性模量，强化阶段模量为弹性模量的1%；σy为屈服应力；εy为屈服应变。

波纹钢板和法兰均采用Q235钢材，分别进行金属拉伸试验，试验结果如表1所示。

表1 材料试验结果Table 1 Material properties obtained from experimental tests

将材料试验所得的工程应力和应变转换为真实应力和应变，得到材料的弹性和塑性参数。钢材密度统一取7 850 kg/m3, 泊松比取0.3。

1.3 模型建立

综合管廊节点模型如图8所示。模型网格划分如图9所示。为保证网格划分质量及模拟结果的精确性，针对螺栓开孔区域进行精细划分，如图10所示。连接节点处受力与破坏状况是本次模拟研究的重点，由于螺栓数量大造成接触对数量过多，易导致计算结果不收敛，已有数值模拟研究中往往采取忽略螺栓的方式。本文采取新方法对螺栓进行优化模拟： 通过在螺栓作用区域中心处添加参考点与法兰耦合，在上下参考点间设置连接器来模拟螺栓预紧力；根据JGJ 82—2011《钢结构高强度螺栓连接技术规程》[20]，10.9S级M20高强螺栓预紧力设置为155 kN，利用“Connector force”将连接器间预紧力定义为155 kN,达到与ABAQUS中“Bolt load”模块相同的效果。环向法兰和纵向法兰之间采用“面面接触”来定义相互关系，充分考虑接触面的切向和法向接触。法向接触使用“Hard”接触传递界面压力；切向采用基于库仑摩擦模型的“Penalty”定义，摩擦因数依据试件表面处理方式确定为0.3[21]。

图8 综合管廊节点模型Fig. 8 Model of utility tunnel joint

图9 模型网格划分Fig. 9 Model meshing

图10 螺栓开孔区域精细划分Fig. 10 Fine division of bolt opening area

1.4 加载方式与加载制度

为模拟钢波纹管廊在纵向、横向、竖向3个不同方向低周往复荷载作用下的破坏情况，本文设计6种加载工况，即横向拉压试验、横向弯剪试验、竖向弯剪试验、纵向拉压试验、横向剪切试验、竖向剪切试验，分别命名为工况1、2、3、4、5、6。为模拟循环荷载，在加载端形心处设置参考点，在此基础上完成与管廊结构加载区域的耦合，加载过程可通过向参考点直接施加荷载或位移完成，加载模式及选取依据[22]如图11所示。

图11 加载模式及选取依据[22]Fig. 11 Loading mode and selection basis[22]

在地震作用下，地下结构本身的自振特性对其地震响应影响较小，对地下结构影响最大的是场地位移。地下结构拟静力试验可用于模拟土体变形对结构的影响，通常应当在结构与土体接触位置处施加单调递增的等效惯性加速度来实现，但考虑到试验对象为单层单跨的箱涵结构，因而可以简化为质量集中于顶端的单自由度体系。另外，本试验主要研究在横向、纵向、竖向位移作用下的结构破坏情况，因而和位移分布形式关系不大。综上，采用顶端单点加载的拟静力试验是可行的[14]。

本次数值模拟的加载制度参考美国ATC-24的标准[23]，采用位移控制加载方式，以屈服位移δy为控制参数，加载幅值按照0.5δy、0.75δy、δy、2δy、3δy、4δy…逐级增加，在达到屈服位移之前每级循环3次，δy、2δy、3δy每级循环3次，之后每级循环2次，加载制度如图12所示。对于屈服位移的确定，先对6种工况进行单调加载，根据得到的荷载-位移曲线，采取一次垂线法[24]确定屈服点。同时，根据取整和偏保守的原则，工况1δy取25 mm，工况2δy取15 mm，工况3δy取10 mm，工况4δy取5 mm，工况5δy取15 mm，工况6δy取20 mm。当试件承载力下降至极限承载力的85%或试件发生破坏时，停止加载。

图12 加载制度Fig. 12 Loading system

1.5 有限元模型验证

为验证本次有限元建模的合理性及建模方法的可行性，对工况1横向拉压、工况2横向弯剪开展拟静力试验，如图13所示。

(a) 工况1横向拉压试验

(b) 工况2横向弯剪试验图13 拟静力试验布置图Fig. 13 Layout of quasi-static test

滞回曲线又称恢复曲线，反映结构在循环往复受力过程中的变形特征、刚度强度退化及能量耗散等。有限元模拟与试验所得到的滞回曲线对比如图14所示。

(a) 工况1横向拉压试验

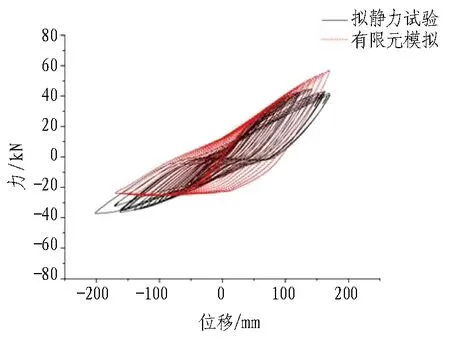
(b) 工况2横向弯剪试验图14 滞回曲线对比Fig. 14 Comparison of hysteresis curves

骨架曲线是试件或结构在循环荷载作用下，每级荷载第一个循环周期内峰值点的连线，反映了结构的承载力、刚度及延性等重要指标。有限元模拟与试验所得到的骨架曲线对比如图15所示。

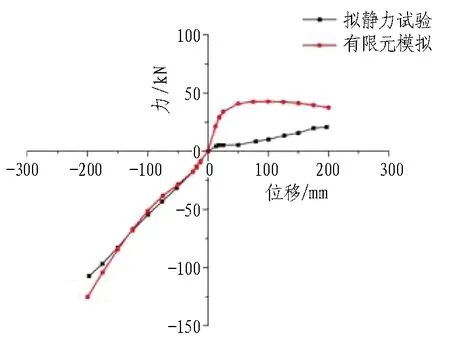
(a) 工况1横向拉压试验

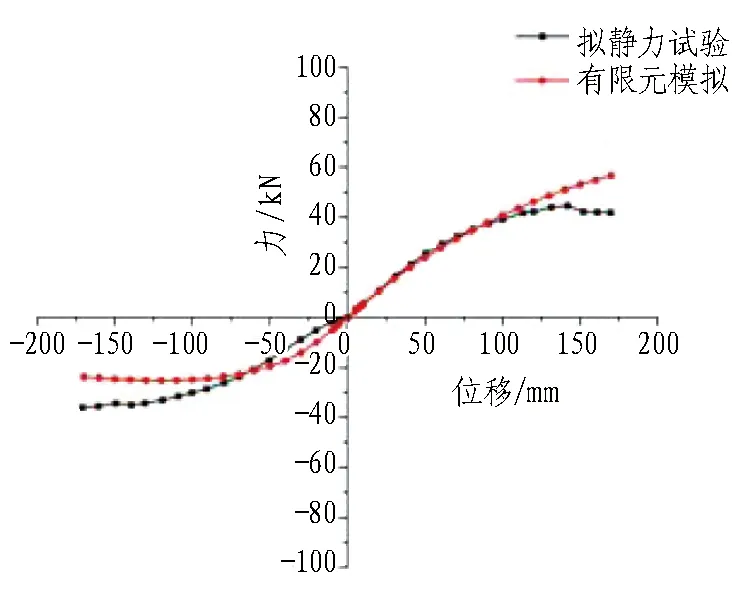
(b) 工况2横向弯剪试验图15 骨架曲线对比Fig. 15 Comparison of skeleton curves

工况1有限元数值模拟滞回曲线在负向上的峰值与试验结果相吻合；但在正向上，由于安装过程中施加+130 mm的位移导致试件尚未试验便已经进入塑性阶段，不但使得滞回曲线在正向上吻合较差，而且影响了负向滞回曲线的饱满度。工况2有限元数值模拟滞回曲线与试验结果吻合度高，由于底部锚固装置在试验中的微小滑移，试验滞回曲线在加载位移0 mm附近出现“捏缩”现象，而数值模拟中边界条件为理想状态，故数值模拟结果在此处未出现“捏缩”。工况2试验结果在加载量大于140 mm后，滞回曲线出现明显的“捏缩”现象，其原因是试件底部焊接锚固处逐渐发生破坏，而数值模拟因其边界条件为理想状态，滞回曲线在此处无“捏缩”现象。总体而言，2种工况下数值模拟得到的滞回曲线饱满度均大于试验结果。其原因可能是： 一方面，数值模拟中采用的钢材本构模型为二折线简化模型，与实际应力-应变曲线仍有差异；另一方面，试验过程中千斤顶加载为手动控制，卸载速度可能存在过快的情况，从而导致这一差异。

2种工况下，在加载前期结构处于弹性阶段时，数值模拟与试验结果吻合较好；但随着加载量增大，试件逐渐进入塑性屈服阶段，骨架曲线的误差也逐渐增大。其原因是： 试验过程中，底部锚固装置不可避免地发生滑移、转动甚至破坏，而有限元模型采用的是人工边界条件，刚度远大于试验情况，因而到加载后期骨架曲线产生的误差逐渐增大。

从总体上看，除去安装因素与理想边界条件的影响，有限元模拟的结果与试验结果吻合度良好，从而验证了本文有限元模型及建模方法的合理性与准确性，后续分析均以此为据。

2 数值模拟结果分析

2.1 应力分析

6种工况加载完成后的应力云图见图16。试件加载过程中，对于工况1，在纵向法兰与波纹钢板连接处应力较大，而在其他位置应力较小；对于工况2，应力在波纹钢板左侧端部(焊接锚固区域)达到极限应力值，且这一区域波纹钢板发生了断裂，其余位置应力则相对较小；对于工况3，应力同样在左侧锚固区域较大，左侧管片的应力大于右侧管片，管廊与法兰连接处应力相对较小；对于工况4，由于波纹钢板在纵向上固有的“手风琴效应”(指波纹钢板在纵向能够自由伸缩[25])使得结构应力分布较为均匀，在管片拼接处环向法兰间出现明显的张开现象，锚固区域及加载端达到极限应力；对于工况5与工况6，其应力分布规律相同，在锚固区域均达到极限应力值，法兰与波纹钢板连接区域应力值均较大。在加载过程中，圆角部分的应力大于侧板区域。

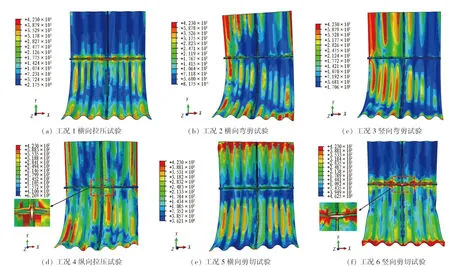
图16 综合管廊应力云图(单位： MPa)Fig. 16 Stress nephograms of specimens (unit: MPa)

在剪切试验中，法兰均发生了较大的变形并在管片拼接处出现张开现象；在横向剪切力作用下，圆角处纵向法兰发生弯折；在竖向剪切力作用下，纵向法兰出现较大的变形，在与波纹钢板连接区域达到极限应力，均有断裂风险。因此，在剪切力作用下，应重视法兰与管廊连接处设计。从总体上看，管廊在圆角处的应力大于侧板。

2.2 滞回曲线

工况1—2的滞回曲线如图14所示，工况3—6的滞回曲线如图17所示。分析6种滞回曲线可知： 在加载量小于屈服位移时，位移与承载力的增长呈线性关系，且卸载后基本没有残余变形，管廊处于弹性状态；随着加载量增大，滞回曲线形状发生改变，说明结构进入弹塑性工作阶段，此时滞回曲线的包络面积逐渐增大，结构耗能也逐渐增大，卸载后结构产生残余变形。

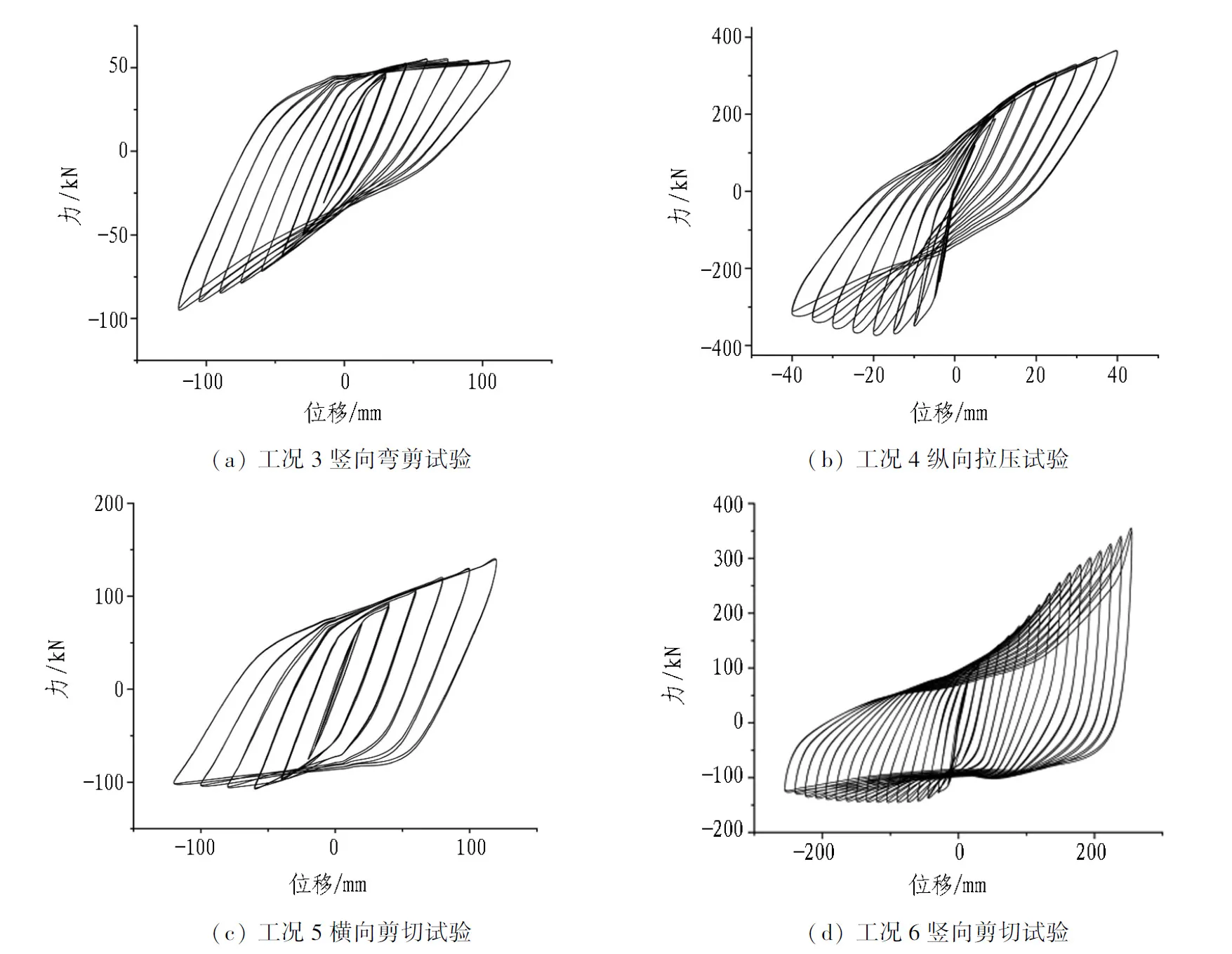
图17 工况3—6滞回曲线Fig. 17 Hysteretic curves under loading conditions 3 to 6

对于工况1，结构的滞回环在负向比正向更加饱满，说明结构在负向上耗能能力良好。从数值模拟结果来看，滞回曲线无论是在正向还是负向的形状均向“Z”形发展，说明结构受到大滑移的影响，其原因是纵向法兰间出现了脱开现象。

工况2与工况3试验中所得到的滞回曲线较为饱满，滞回环呈“梭形”，说明结构在弯剪力作用下具有良好的耗能能力。

工况4在加载初期的滞回环呈“Z”形，但随着加载量的增大，滞回环向“梭形”发展，包络面积不断增大，耗能能力也逐步增强，主要是波纹板纵向受力时具有良好的“手风琴效应”，通过伸缩过程，结构能够吸收大量能量，从而改善结构的抗震性能。同时，工况4滞回环的对称性也随加载位移的增长而发生变化。在加载前期，负向(受压)滞回环饱满度高于正向(受拉)，而随着加载位移的增大，滞回环正负向逐渐对称。其原因是： 一方面，波纹钢板在纵向抗拉强度和抗压强度上存在差异；另一方面，波纹钢板在纵向受拉时环向法兰间较早出现脱开现象，而此时波纹钢板尚未屈服，这也是加载初期滞回环呈“Z”形的原因。

工况5所得到的滞回曲线最为饱满。弹性阶段结构几乎不耗能，但在进入塑性阶段后，滞回曲线包络面积迅速增大，耗能能力显著增强，说明结构抵抗横向剪切地震力的能力较好。

工况6中滞回曲线呈“Z”形，说明结构受到大滑移的影响。分析该工况位移云图可知： 在竖向循环剪切力作用下，纵向法兰之间脱开现象严重，且上部平直段管片在竖向力作用下也发生较大的位移和转角，这也表明波纹钢板的抗弯能力较弱。

在横向、竖向、纵向循环往复荷载作用下，结构滞回曲线均出现“捏缩”现象，部分原因是法兰、波纹钢板与法兰连接处发生局部屈曲变形[26]。由图16可以看出，结构局部屈曲变形较为严重，这在一定程度上削弱了波纹钢板综合管廊的抗震性能。而工况4与工况6中滞回曲线的 “捏缩”现象较为严重，其原因是这2种工况下连接法兰之间的脱开现象最为严重。此外，对于工况4，由于波纹钢板自身存在“手风琴效应”，结构的纵向变形较大也加重了滞回曲线出现“捏缩”现象。

2.3 骨架曲线与延性系数

工况1—2的骨架曲线如图15所示，工况3—6的骨架曲线如图18所示。分析图15和图18骨架曲线可知： 6种工况下，结构均经历了从屈服到达到极限荷载再到承载力下降的阶段。当加载量小于结构的屈服位移时，骨架曲线近似为一条直线，说明荷载和加载位移基本呈线性关系。结构屈服后，其刚度降低，骨架曲线逐渐变得平缓并发生弯曲。

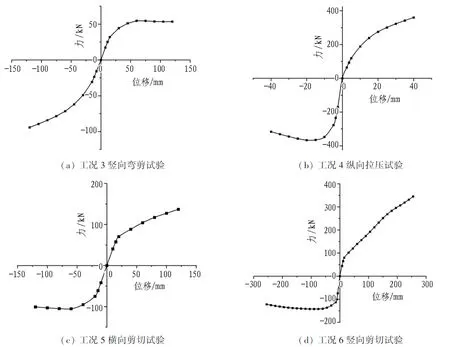
图18 工况3—6骨架曲线Fig. 18 Skeleton curves under loading conditions 3 to 6

对于工况1，结构负向承载力与位移呈线性增长，并且无下降段；而在正向上，加载量达到+75 mm时骨架曲线进入下降段。正向极限承载力为42.6 kN，负向最大承载力为125.4 kN，负向承载力比正向承载力高194.3%以上。

对于工况2，位移加载至-120 mm时，负向承载力达到极限并开始下降，而正向承载力不受影响且继续增大。正向承载力比负向承载力高123.8%以上。

对于工况3，位移加载至+60 mm时，正向承载力达到极限并开始下降，而负向承载力继续增大且无下降段。负向承载力比正向承载力高75%以上。

对于工况4，正向极限承载力与负向极限承载力基本相同，但骨架曲线在加载负向出现下降段，而在加载正向未进入屈服平台，即结构在纵向上抗拉承载力高于抗压承载力。

对于工况5，位移加载至-60 mm时，试件在负向达到极限承载力，正向承载力比负向承载力高26.3%。

对于工况6，位移加载至-90 mm时，试件达到极限承载力，正向承载力比负向承载力高143%。

数值模拟中得到的正负承载力差异较大的原因是： 一方面，受到环向法兰易发生脱开现象的影响；另一方面，横截面圆角部分的存在对结构在竖向的力学性能产生重要影响。

延性系数是衡量结构弹塑性变形能力的重要指标，结构延性系数μ按式(2)[27]计算。根据骨架曲线，试件的屈服点按一次垂线法确定[24]： 试件所能承受的最大荷载作为极限荷载Fu, 此时位移作为极限位移Δu，以极限荷载水平线与初始刚度线交点的横坐标作为屈服位移Δy，对应的荷载作为屈服荷载Fy，如图19所示。

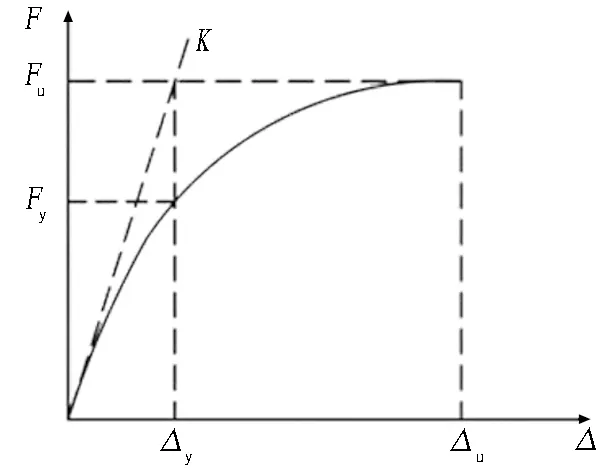
图19 屈服点确定方法Fig. 19 Determination method of yield point

(2)

根据骨架曲线数据以及式(2)、图19的方法获得6种工况的延性系数，如表2所示。

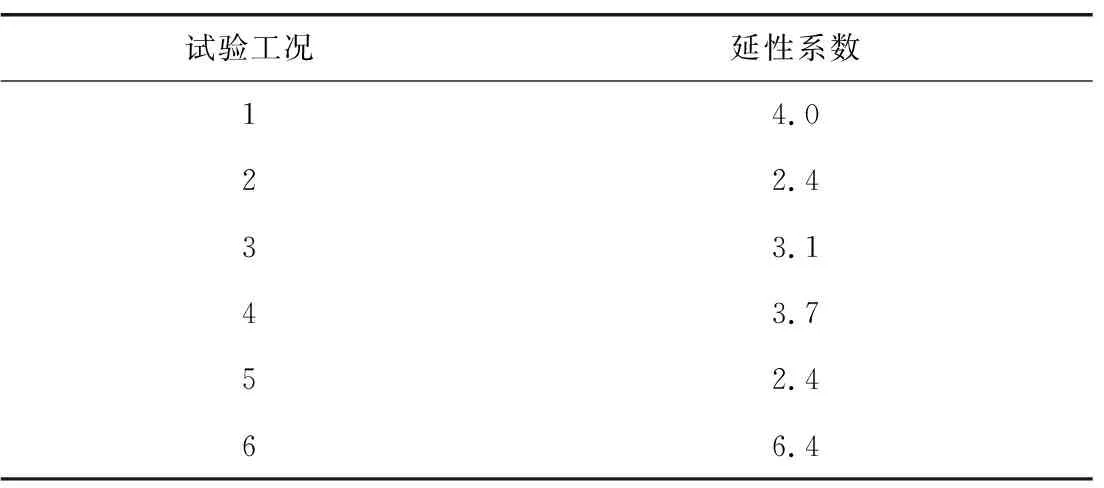
表2 6种工况的延性系数Table 2 Ductility coefficient of six loading conditions

延性系数越大，表明结构在强震作用下能承受越大的塑性变形而不发生破坏。对于钢结构而言，延性系数大于2，则认为该结构具有良好的塑性变形能力。由表2可知，波纹钢板综合管廊塑性变形性能良好，从总体上看结构竖向延性系数最高，塑性变形能力最优。

2.4 刚度退化与强度退化

2.4.1 刚度退化

刚度退化是指在低周循环荷载作用下，随着荷载循环次数的增加，结构或者构件的位移不断增大，刚度不断减小的现象。试件的刚度用割线刚度表示，见式(3)[27]。

(3)

式中： +Fi、-Fi分别为第i次正、反向峰值点的荷载值； +Xi、-Xi分别为第i次正、反向峰值点的位移值。

取每级荷载第1次循环峰值点的割线刚度表示结构的刚度退化，以加载端位移为X轴，割线刚度为Y轴，绘制试件刚度退化曲线，如图20所示。由图可以看出： 6种工况下试件的刚度退化曲线趋势基本相同。在加载前期，加载量小于结构的屈服位移时，刚度曲线较陡，刚度退化较快；超过屈服位移之后，曲线逐渐趋于平缓，刚度退化逐渐变慢；达到极限荷载后，刚度曲线趋于平直。纵向结构刚度远大于其他方向。加载结束后，从工况1到工况6结构残余刚度较初始刚度分别降低了65.5%、53.1%、72.1%、82.0%、80.0%和88.4%。说明结构在剪切力与纵向拉压力作用下刚度退化幅度最大。试件纵向刚度远大于横向与竖向，由于波纹板的“手风琴效应”，使得结构能够在纵向循环荷载作用下具有良好的耗能能力。

图20 刚度退化曲线Fig. 20 Stiffness degradation curves

2.4.2 强度退化

强度退化是指结构或构件施加相同位移的情况下，承载力随着循环次数的增加而略有降低的现象，一般用强度退化系数λi表示，见式(4)[27]。

(4)

表3—8示出6种工况的强度退化系数计算结果。由表可知： 结构在3个不同方向的低周循环往复荷载作用下，随着加载循环j增加逐渐出现强度退化现象；但强度退化系数均大于0.95，结构强度退化幅度很小，说明结构在循环往复荷载作用下具有较稳定的承载能力。

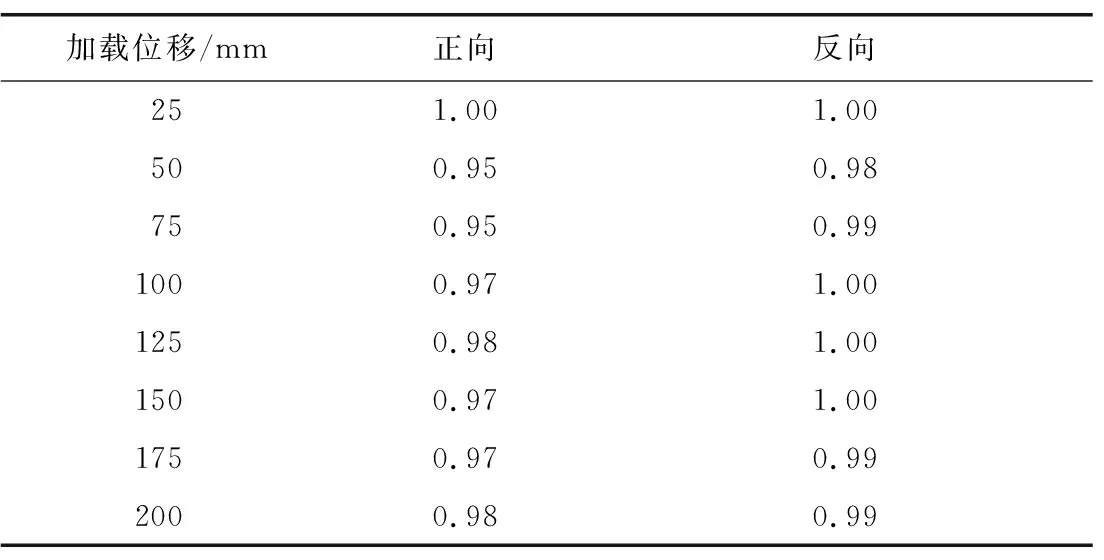
表3 工况1强度退化系数Table 3 Strength degradation coefficient of condition 1

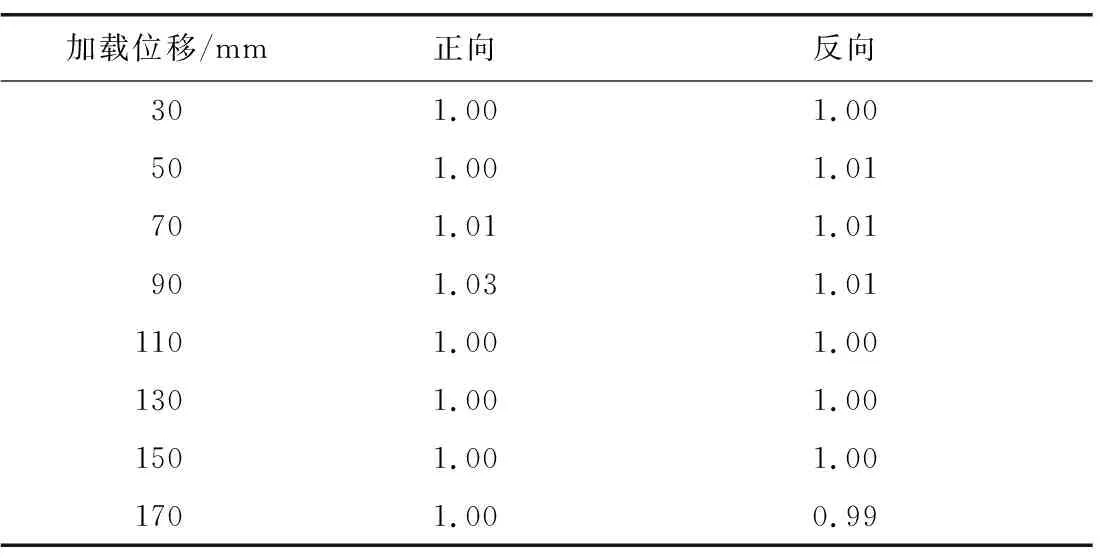
表4 工况2强度退化系数Table 4 Strength degradation coefficient of condition 2

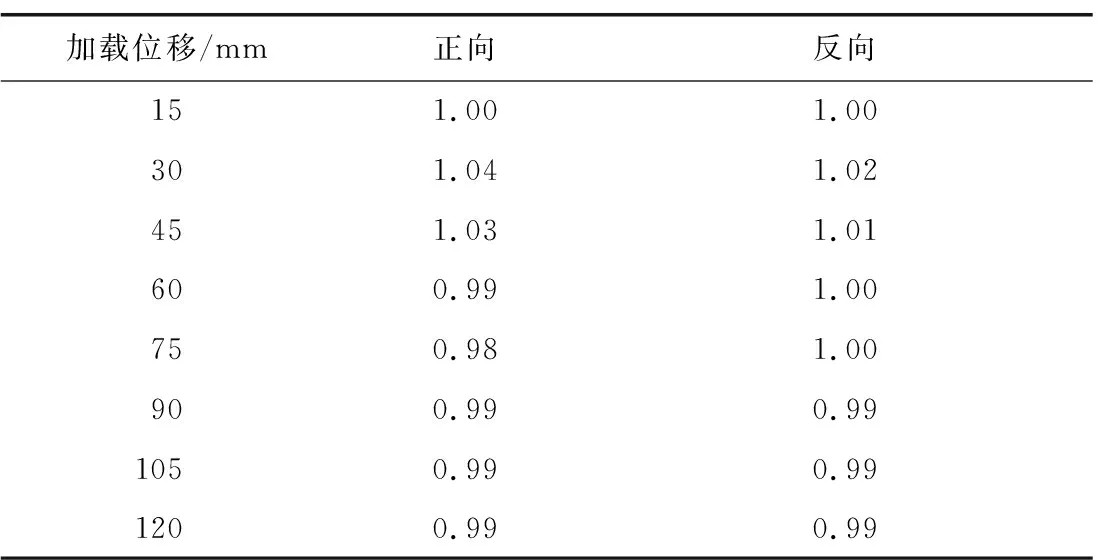
表5 工况3强度退化系数Table 5 Strength degradation coefficient of condition 3

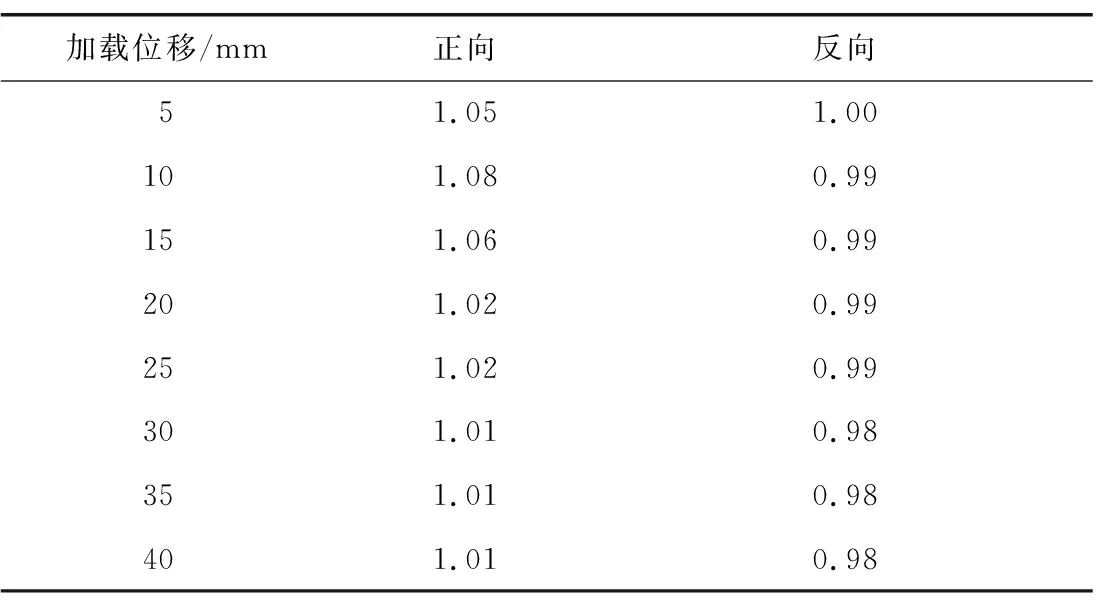
表6 工况4强度退化系数Table 6 Strength degradation coefficient of condition 4

表7 工况5强度退化系数Table 7 Strength degradation coefficient of condition 5

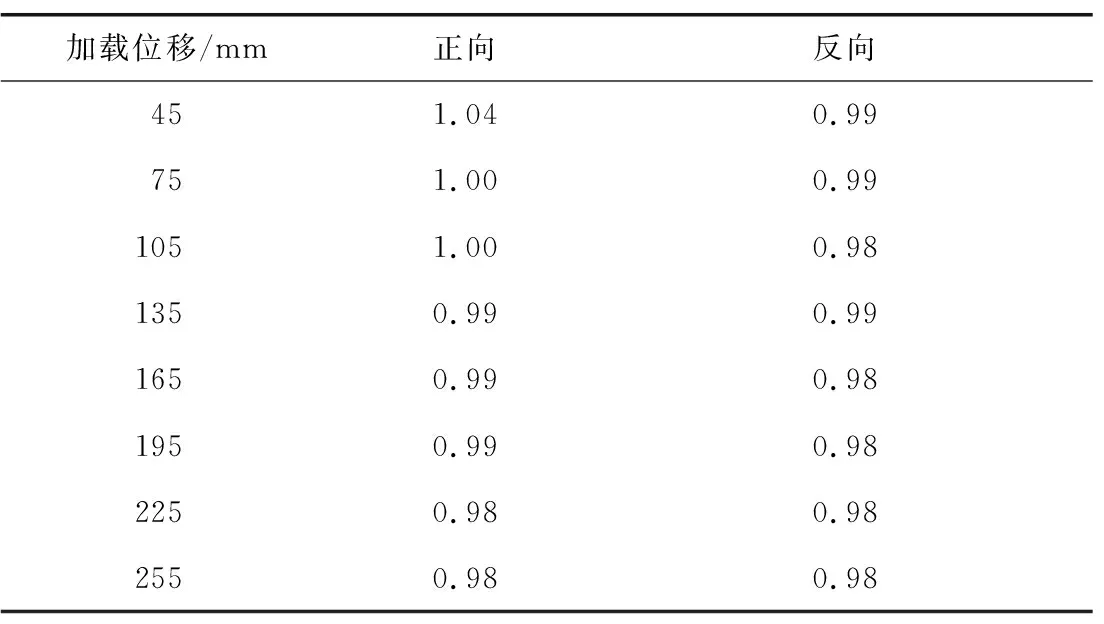
表8 工况6强度退化系数Table 8 Strength degradation coefficient of condition 6

2.5 耗能能力

耗能能力能够反映结构或构件的抗震性能。耗能能力通过滞回曲线包络面积衡量，通常用能量耗散系数E或等效黏滞阻尼系数ζeq来表示(见图21)，见式(5)和式(6)[27]。

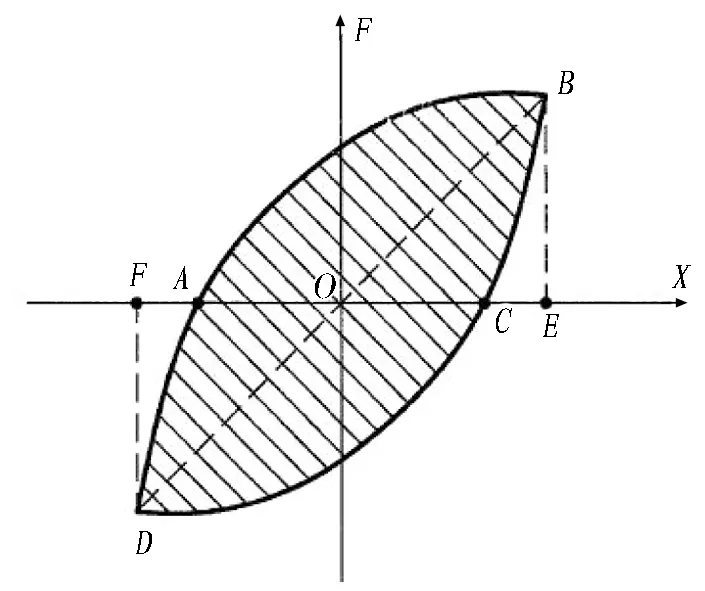
图21 E与ζeq计算示意图Fig. 21 Calculation diagram of E and ζeq

(5)

(6)

式中：S(ABC+CDA)为图21中滞回曲线包络面积；S(OBE+ODF)为△OBE与△ODF的面积之和。

按照式(5)与图21方法计算能量耗散系数E， 6种工况在不同峰值荷载下的能量耗散系数如图22所示。

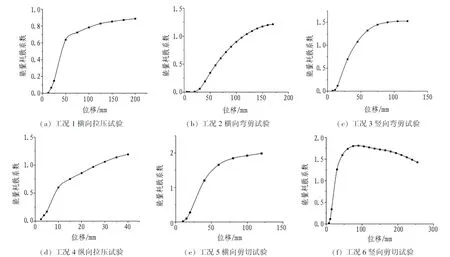
图22 能量耗散系数Fig. 22 Energy dissipation coefficients

能量耗散系数E是结构变形吸收的能量与地震输入结构的最大能量之比[28]，该指标越大，说明结构吸收地震能量的能力越强，抗震性能越好。就同一结构而言，不同阶段的能量耗散系数是不同的。根据图22可知： 加载位移小于屈服位移时，试件能量耗散系数E较小；而当加载位移超过屈服位移之后，E迅速增大，表明试件耗能能力增大。工况1—5能量耗散系数一直呈上升趋势，除工况1外，其最大值均超过1，说明结构在该受力方向上不仅具有良好的耗能能力，还拥有一定的耗能储备。工况6中试件能量耗散系数E在加载位移为90 mm时达到极值，随后开始下降，但加载完成后E仍大于1。从总体上看，波纹钢板综合管廊在各方向循环往复荷载作用下具有良好的耗能能力。

3 有限元参数化分析

3.1 连接节点对结构抗震性能影响

3.1.1 滞回曲线对比

由第2节可知，法兰的存在对管廊的抗震性能具有重要影响。为探究法兰作用机制，本文建立未考虑节点连接的模型(无法兰连接)与考虑节点连接的模型(有法兰连接)进行对比。

不同连接节点滞回曲线对比如图23所示。由图可以看出，法兰的存在对结构的滞回性能有显著影响。相比于考虑节点连接的模型，未考虑节点连接的模型在纵向、横向和竖向的滞回曲线均更加饱满。这说明法兰的存在会对结构的滞回性能产生不利影响；同时，“捏缩”效应明显减轻，原因是局部屈曲现象得到改善，工况4与工况6中的“捏缩”效应改善最为明显，也证明法兰之间脱开现象对结构的滞回性能有显著影响。在实际工程中应采取有效措施对法兰间连接进行加固。

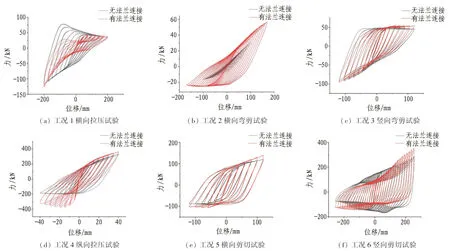
工况2加载至100 mm时试件部分区域已屈服，网格发生畸变而无法继续计算。图23 不同连接节点滞回曲线对比Fig. 23 Comparison of hysteresis curves of different joints

3.1.2 骨架曲线对比

不同连接节点骨架曲线对比如图24所示。从整体来看，有法兰连接和无法兰连接的骨架曲线发展趋势基本一致，但法兰的存在对结构的承载力具有一定的提升作用，该提升作用在工况4中尤为显著。具体而言，法兰的存在对纵向承载力正向提升8.37%，负向提升90.59%。其余工况正向与负向极限承载力均略有提高。法兰能够提升结构的承载能力，原因是其在整体结构中起到了加劲肋的作用。

图24 不同连接节点骨架曲线对比Fig. 24 Comparison of skeleton curves of different joints

3.1.3 刚度退化曲线对比

不同连接节点刚度退化曲线对比如图25所示。由图可以看出，法兰对结构的初始刚度有较大的影响。法兰在整个结构中起到了类似于加劲肋的作用，因而对结构的初始刚度有较大的提升作用。工况1和6中结构的初始刚度提升幅度较小，说明纵向法兰对结构整体的初始刚度贡献不大。6种工况的刚度退化趋势基本一致，加载初期较陡，最后趋于平缓，加载完成后结构的残余刚度几乎一致，表明法兰在循环往复荷载作用下发生了较为严重的损伤。

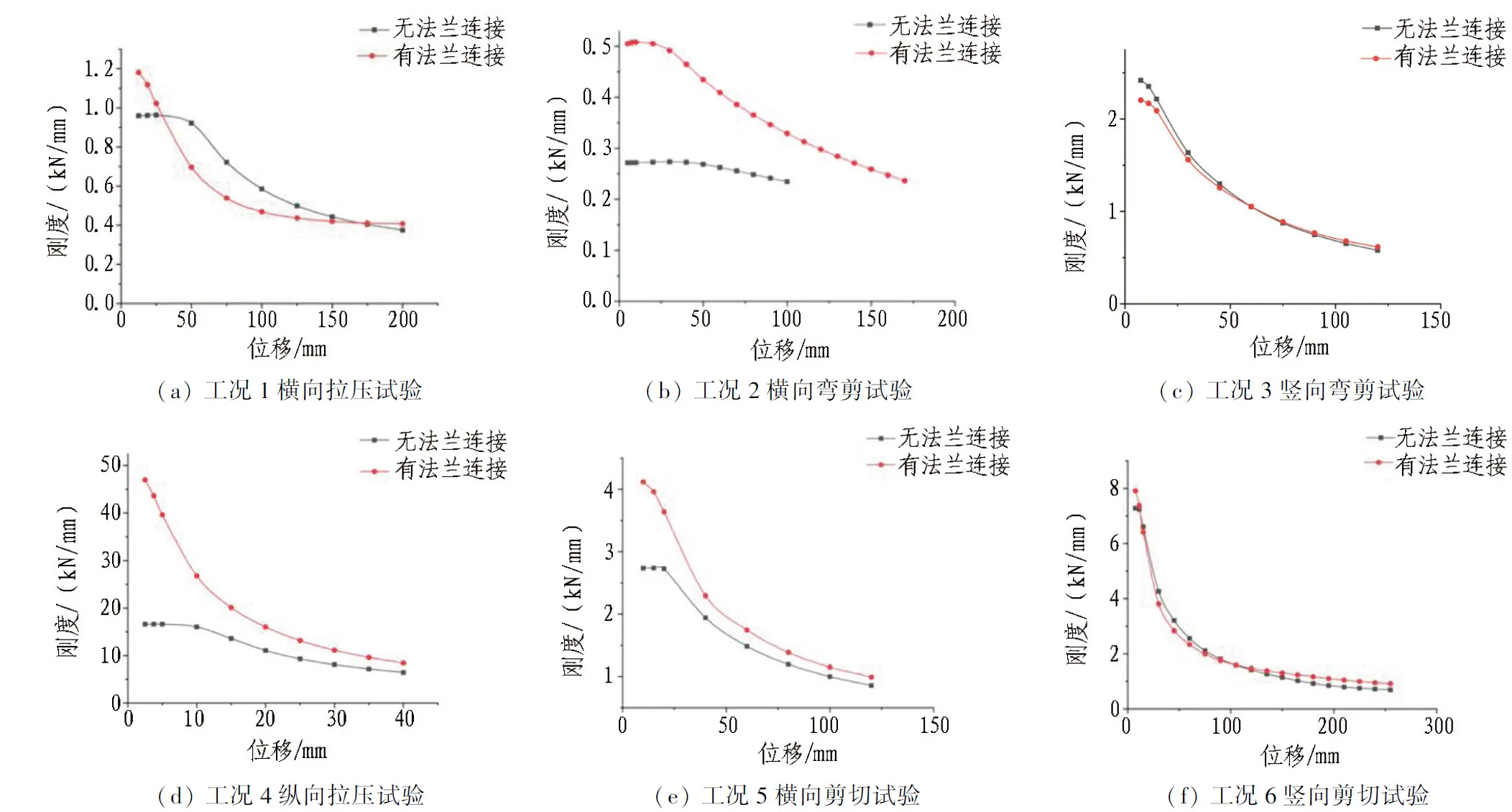
图25 不同连接节点刚度退化曲线对比Fig. 25 Comparison of stiffness degradation curves of different joints

3.1.4 能量耗散系数对比

不同连接节点能量耗散系数对比如图26所示。由图可以看出，相比有法兰连接结构，无法兰连接结构的能量耗散系数明显提升，耗能能力更优，且6种工况的最大能量耗散系数均大于1。二者的耗能能力发展趋势基本保持一致，无法兰连接时，虽然E在下降段降幅较大，但其均大于有法兰连接时的E值。总体来看，无法兰连接结构的耗能能力远优于有法兰连接结构，即法兰的存在对结构耗能能力产生不利影响。

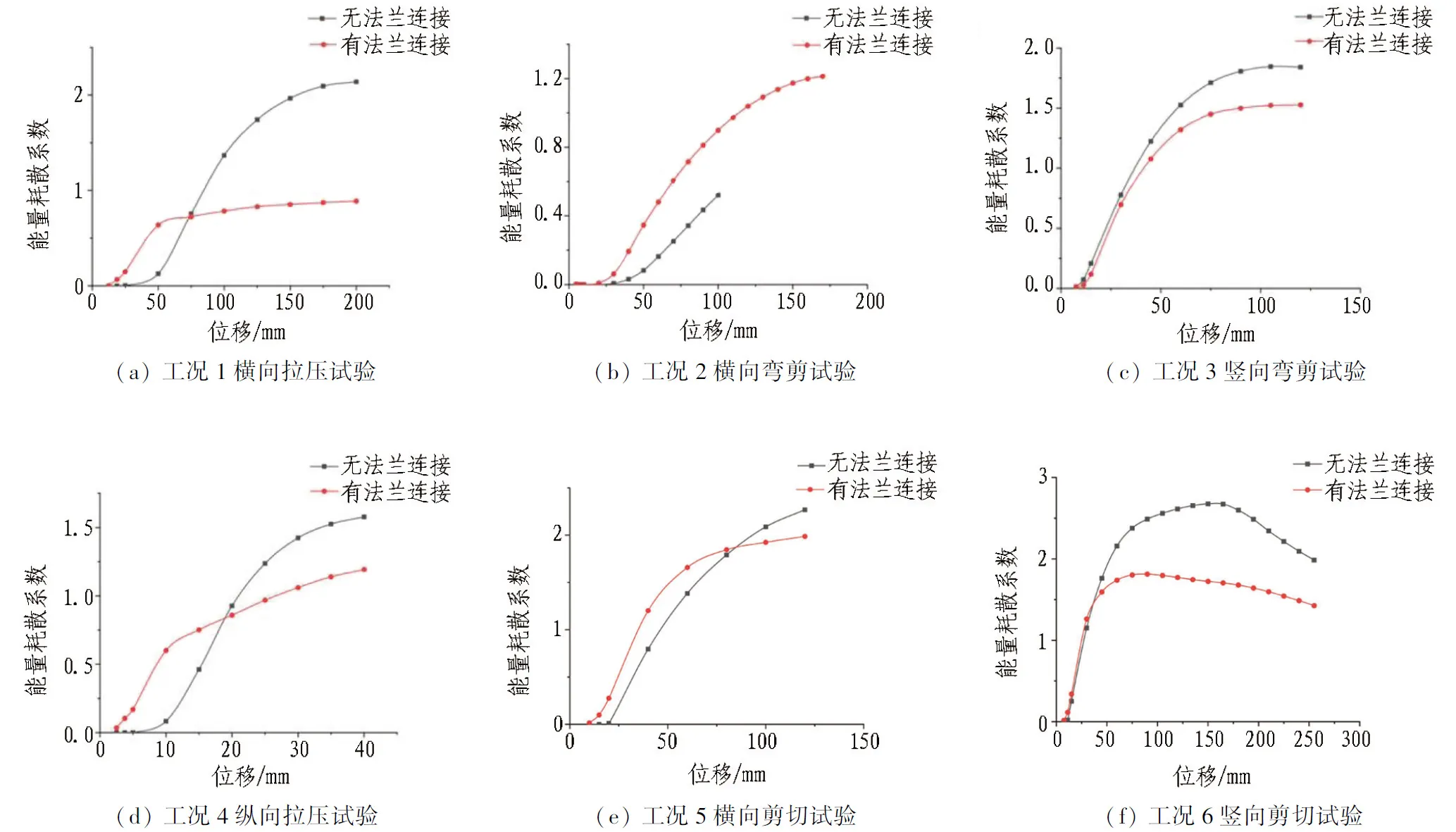
图26 不同连接节点能量耗散系数对比Fig. 26 Comparison of energy dissipation coefficients of different joints

3.2 法兰厚度对结构抗震性能影响

为探究法兰厚度对管廊抗震性能的影响，本文分别建立法兰厚度为7、8、10、11 mm的结构与原模型(法兰厚度为9 mm)进行对比。

3.2.1 滞回曲线对比

不同法兰厚度滞回曲线对比如图27所示。由图可以看出，不同法兰厚度的管廊的滞回曲线形状保持一致。随着法兰厚度的增加，结构滞回曲线包络面积增大，但增幅较小，同时试件的“捏缩”现象略有改善，原因是随着法兰厚度的增加，一方面试件局部屈曲现象得到改善，另一方面纵向法兰与环向法兰之间的脱开减小。从总体上看，法兰厚度对结构的滞回曲线的影响较小。

图27 不同法兰厚度滞回曲线对比Fig. 27 Comparison of hysteresis curves of different flange thickness

3.2.2 骨架曲线对比

不同法兰厚度骨架曲线对比如图28所示。由图可以看出，法兰厚度对骨架曲线走向无明显影响，骨架曲线形状保持一致。对于工况3、5、6，5种法兰厚度的骨架曲线基本重合，说明法兰厚度对竖向和纵向的承载力影响较小。而工况1负向极限承载力提升57.6%，正向最大承载力提升16.1%；工况2负向最大承载力提升5.3%，正向最大承载力提升14.2%；工况4负向极限承载力提升3.2%，正向最大承载力提升36.9%；结果表明，法兰厚度的增加对结构的横向抗弯承载力及纵向抗拉承载力有明显提升。

图28 不同法兰厚度骨架曲线对比Fig. 28 Comparison of skeleton curves of different flange thickness

3.2.3 刚度退化曲线对比

不同法兰厚度刚度退化曲线对比如图29所示。由图可以看出，法兰厚度的增加也相应提高了结构在横向、纵向、竖向3个方向的初始刚度。不同法兰厚度的结构刚度退化趋势相一致，加载初期刚度退化速率均较快，加载完成后结构残余刚度基本相同。结合3.1节对有无法兰的刚度退化对比可以看出，法兰能提升结构的初始刚度，但改变法兰厚度或无法兰的情况下，残余刚度均基本保持一致，说明法兰在循环荷载作用下会发生严重破坏。总体而言，法兰厚度提升对刚度退化影响较小。

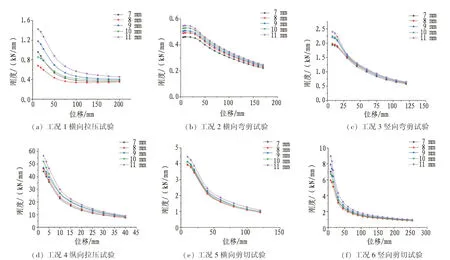
图29 不同法兰厚度刚度退化曲线对比Fig. 29 Comparison of stiffness degradation curves of different flange thickness

3.2.4 能量耗散系数对比

不同法兰厚度能量耗散系数对比如图30所示。从总体趋势上看，随着法兰厚度增加，结构能量耗散系数也逐步增大。工况1、4增幅略大，结构横向及纵向耗能能力得到提高；而工况2、3结构能量耗散系数几乎无改变。对于工况5、6，随着法兰厚度增加，结构能量耗散系数甚至出现下降，可见法兰厚度的增加，会在结构受剪切力作用时降低其耗能能力。6种工况的能量耗散系数发展趋势仍保持一致，E值均大于1，结构在纵向、横向、竖向上耗能能力良好。法兰厚度增加对不同方向及不同形式荷载作用下结构的耗能能力产生不同甚至相反的影响，但该影响较小。

图30 不同法兰厚度能量耗散系数对比Fig. 30 Comparison of energy dissipation coefficients of different flange thickness

3.3 波纹钢板厚度对结构抗震性能影响

为研究波纹钢板厚度对结构抗震性能的影响，本文建立壁厚为4、5、7、8 mm的波纹钢板综合管廊与原模型(壁厚6 mm)进行对比，分析结果如下。

3.3.1 滞回曲线对比

不同管廊壁厚滞回曲线对比如图31所示。由图可以看出： 对于工况1，管廊壁厚的提升对其滞回曲线影响较小；对于工况2、3、4、5，随着管廊壁厚的增加，滞回曲线形状逐渐向梭形发展，包络面积也逐渐增大；对于工况6，滞回曲线形状无改变，但其包络面积增大。从总体上看，随着波纹钢板综合管廊壁厚的增加，滞回曲线包络面积也不断增大，形状愈加饱满，表明结构的耗能能力得到显著提升。

图31 不同管廊壁厚滞回曲线对比Fig. 31 Comparison of hysteresis curves of different tunnel thickness

3.3.2 骨架曲线对比

不同管廊壁厚骨架曲线对比如图32所示。由图可以看出，随着管廊壁厚的增加，骨架曲线的形状及发展趋势仍然保持一致，结构的极限承载力也显著增大。管廊壁厚8 mm相较于壁厚4 mm，工况1最大承载力负向提升48.4%；工况2最大承载力负向提升268.4%，正向提升184.5%；工况3最大承载力负向提升184.6%, 正向提升242.3%；工况4最大承载力负向提升150.8%，正向提升56.0%；工况5最大承载力负向提升89.1%，正向提升70.2%；工况6最大承载力负向提升76.6%，正向提升49.3%。综合来看，增加管廊壁厚对结构承载力有显著提升。

图32 不同管廊壁厚骨架曲线对比Fig. 32 Comparison of skeleton curves of different tunnel thickness

3.3.3 刚度退化曲线对比

不同管廊壁厚刚度退化曲线对比如图33所示。由图可以看出，随着管廊壁厚的增加，结构的初始刚度均有了显著提升，工况2、3、4、5初始刚度提升幅度较大且均超过200%，工况1、6初始刚度提升超过50%。加载完成后的残余刚度也与管廊壁厚呈正相关，6种工况残余刚度分别提升40.0%、204.3%、64.4%、98.3%、55.9%、19.6%，说明增加管廊壁厚能显著提升结构的承载力与完整性。总体上看，波纹钢板厚度对管廊的刚度退化有显著影响，增加管廊壁厚能够提升管廊的抗损伤能力。

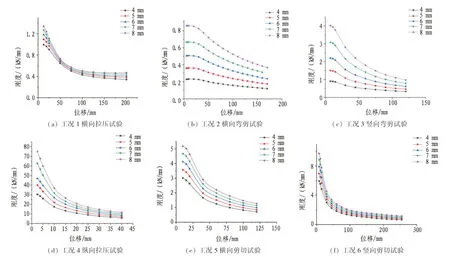
图33 不同管廊壁厚刚度退化曲线对比Fig. 33 Comparison of stiffness degradation curves of different tunnel thickness

3.3.4 能量耗散系数对比

不同管廊壁厚能量耗散系数对比如图34所示。由图可以看出，除工况1能量耗散系数随管廊壁厚增大而略有下降外，其余工况能量耗散系数均随着管廊壁厚的增加而增加，但总体而言变化幅度均较小，能量耗散系数值均超过1。对于工况1、3、4，管廊壁厚较小时，随着加载量增大，能量耗散系数曲线进入平台段甚至下降，而壁厚较大的管廊结构仍保持上升趋势，具有良好的耗能储备，即增加管廊壁厚能够提升结构的耗能能力。

图34 不同管廊壁厚能量耗散系数对比Fig. 34 Comparison of energy dissipation coefficients of different tunnel thickness

3.4 螺栓位置对结构抗震性能影响

由第2节可知，在不同方向低周循环往复荷载作用下，环向法兰之间易发生脱开现象，导致滞回曲线出现“捏缩”现象，进而影响结构的抗震性能。在实际工程应用中，若法兰间发生脱开会导致管廊出现涌水涌砂等事故，而高强螺栓的位置对环向法兰张开距离具有重要影响。本文建立2种不同的螺栓位置布置模型(位于中部及右侧)，与原模型(位于左侧)进行对比，如图35所示，探讨环向法兰螺栓位置对结构抗震性能的影响。

图35 螺栓位置示意图Fig. 35 Schematic of bolt position

3.4.1 滞回曲线对比

不同螺栓位置滞回曲线对比如图36所示。由图可以看出，环向法兰上螺栓位置的改变对工况1、2、3、5、6滞回曲线几乎无影响；但对于工况4纵向拉压试验的滞回曲线有着显著影响，螺栓位置越偏向于外侧(接近法兰与波纹钢板连接部位)，滞回曲线愈加饱满、包络面积显著增大，能耗水平不断提高，其主要原因是环向法兰间的脱开现象得到改善。滞回曲线正向出现明显“捏缩”现象，其原因是法兰与管廊连接处及环向法兰局部屈曲较为严重。

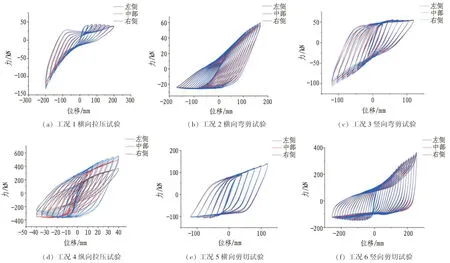
图36 不同螺栓位置滞回曲线对比Fig. 36 Comparison of hysteresis curves of different bolt positions

3.4.2 骨架曲线对比

不同螺栓位置骨架曲线对比如图37所示。由图可以看出，工况4正向(受拉)承载力提升52.8%，负向(受压)承载力降低-1.9%，螺栓的位置对于纵向抗拉承载力有一定提升作用。除工况2外，其余工况骨架曲线基本保持不变，即改变环向法兰螺栓位置仅对纵向承载力有显著影响。

图37 不同螺栓位置骨架曲线对比Fig. 37 Comparison of skeleton curves of different bolt positions

3.4.3 刚度退化曲线对比

不同螺栓位置刚度退化曲线对比如图38所示。可以看出，对于工况2、3、4，螺栓开孔位置位于法兰右侧(外侧)较左侧(内侧)对初始刚度有一定提升作用，初始刚度分别提升8.9%、19.2%、23.2%；对于剩余工况，其刚度退化曲线基本保持一致。因此，改变螺栓位置能够提升结构在地震作用下的承载力与整体性。

图38 不同螺栓位置刚度退化曲线对比Fig. 38 Comparison of stiffness degradation curves of different bolt positions

3.4.4 能量耗散系数对比

不同螺栓位置能量耗散系数对比如图39所示。由图可以看出，对于工况4纵向拉压试验，螺栓位置设置在右侧时，能量耗散系数增大能够显著提升结构的耗能能力，且螺栓设置在右侧比左侧最大能量耗散系数提高约72.0%；其他工况能量耗散系数基本保持不变。

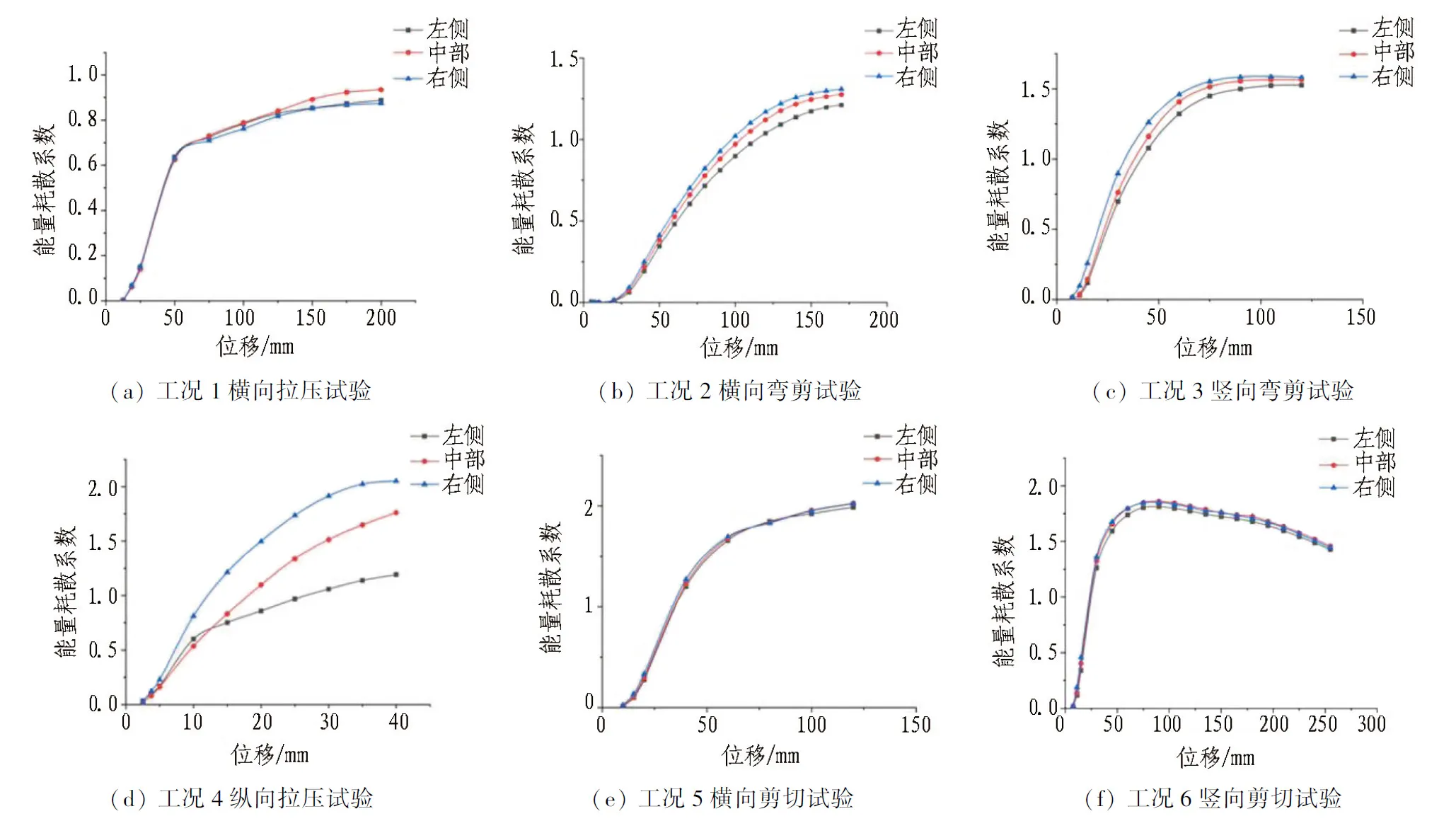
图39 不同螺栓位置能量耗散系数对比Fig. 39 Comparison of energy dissipation coefficients of different bolt positions

综上所述，对于波纹钢板综合管廊，改变环向法兰螺栓位置对纵向抗震性能有重要的影响。将螺栓布置在外侧位置，不仅提升了结构在纵向的耗能能力，还有效提高了结构的承载力与刚度。因此，在波纹钢板综合管廊设计过程中，在满足安装条件下，应尽可能把螺栓布置在外侧位置(接近法兰和波纹板的连接位置处)。

4 结论与展望

本文通过ABAQUS有限元软件对波纹钢板综合管廊节点进行模拟分析，建立了考虑节点连接的波纹钢板综合管廊精细化有限元模型，详细分析了该结构在纵向、横向和竖向低周循环往复荷载作用下的滞回性能。此外，通过参数分析，探讨了法兰、法兰厚度、管廊板厚、螺栓位置等参数对结构抗震性能的影响。所得结论如下：

1)波纹钢板综合管廊在纵向、横向和竖向循环荷载作用下，结构塑性变形能力强，抗震性能良好；节点拼接处是结构的薄弱点，法兰之间易发生脱开现象；同时，局部屈曲现象较为严重，造成滞回曲线“捏缩”现象；结构刚度退化幅度较大且退化速度较快。但是，其强度基本无明显退化，表明结构仍具有良好的承载能力。

2)波纹钢板综合管廊耗能能力较好，能量耗散系数呈上升趋势。在竖向循环荷载作用下，结构达到极限承载力后虽有下降但其值均大于1，表明结构在竖向上具有良好的耗能能力；在纵向和横向循环荷载作用下，结构能量耗散系数虽小于竖向，但其值一直处于上升阶段，尤其在纵向上，结构仍有较大的耗能储备。

3)法兰连接方式是一种有利于现场装配作业的波纹钢板连接方式，但它的存在对管廊结构抗震性能有显著的影响。法兰虽能起到加劲肋作用，提升结构的极限承载力和整体刚度，但同时也会削弱结构的耗能能力，对结构抗震性能产生不利影响。法兰厚度对结构滞回性能影响较小，但管廊壁厚(波纹钢板厚度)是影响结构滞回性能的关键因素，增大管廊壁厚不仅能够显著提高结构的承载力与刚度，还使得结构滞回曲线更加饱满、耗能能力更优。

4)环向法兰上螺栓开孔位置对结构纵向抗震性能影响较大。建议在满足安装条件下，应尽可能把高强螺栓布置在靠近法兰与波纹钢板的连接处。

本文仅对波纹钢板综合管廊下部节点进行了计算分析，未对整段管廊进行研究。若对管廊整体抗震性能进行探索研究，须使用标准节段的波纹钢板综合管廊作为研究对象；波纹钢板综合管廊的连接方式有多种，本文针对整体拼装式(法兰连接)的波纹钢板管廊展开了研究，对采用其他波纹钢板连接方式有参考和借鉴作用，但其具体的力学特点和抗震性能还有待后续有针对性的比对和研究。