厚松散层底含直覆薄基岩开采地表沉陷预计及特征研究
彭世龙,程 桦,姚直书,荣传新,蔡海兵,张亮亮
(1.安徽建筑大学 建筑结构与地下工程安徽省重点实验室,安徽 合肥 230601;2.安徽理工大学 土木建筑学院,安徽 淮南 232001;3.安徽省矿山生态修复工程实验室,安徽 合肥 230601)
近年来,随着我国煤炭资源逐步进入深部开采,两淮及巨野等矿区相继出现厚松散层薄基岩赋存条件煤炭开采矿井[1-3]。大量观测资料表明[4-7],该类地层采煤活动引起的地表下沉系数明显偏大,部分采区甚至出现大于1的情况,且地表沉陷和水平移动范围相对采区延伸较远。按照常规开采沉陷理论已无法对此现象进行合理解释。如山东巨野矿区某矿厚松散层(500 m以深)薄基岩地层井筒出现井筒偏斜与竖向压缩变形共存的新破损形态,严重威胁矿井安全生产[8-13]。按现行《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》[14](2017版)计算,开采沉陷对其并没影响,无法解释造成井筒偏斜的机理与原因。
国内学者针对厚松散层薄基岩下采煤活动造成的覆岩移动方面开展了一些研究。赵启峰等[15]根据岩层移动分层传递观点,结合厚松散层下开采地表移动特征,建立了厚松散层下煤层开采沉陷预测模型;许延春等[16]通过离散元模拟了不同采矿条件和不同松散层条件下厚松散层、地表移动变形特征;王金庄等[17-18]以邢台矿区东庞矿实测资料为基础,阐述了地表下沉系数偏大和地表移动剧烈等问题,并提出了巨厚松散层下开采的双层介质模型;韩奎峰等[19]以淮南新矿区地表移动观测资料为基础,揭示了概率积分法在厚冲积层矿区应用的主要缺陷,提出了概率积分法预计模型的修正方法;李德海等[20]根据豫东永夏矿区的实测资料,分析了巨厚松散层下开采引起的地表移动特征,阐述了地表采动稳定的判别方法及预计的双重介质模型,得出了厚松散层下开采的地表移动参数与松散层厚度的定量关系以及地表移动期的量化特征。上述研究虽在一定程度上注意到厚松散层移动变形特征,提出了多种地表沉陷预计方法,但未考虑厚松散层底部含水层(以下简称“底含”)直接覆盖于(以下简称“直覆”)薄基岩条件开采疏水沉陷变形中的水土耦合作用,无法深刻揭示该类特殊地层下开采地表沉陷规律。
在开采引起松散层疏水沉降研究方面,国内学者姜岩[21]、刘宝琛[22]、施成华等[23-24],分别对抽取地下水引起的地层疏水沉降、露天矿开挖引起的边坡疏水沉降、基坑和隧道开挖引起的地层疏水问题进行了大量研究;狄乾生等[25]总结了矿区厚含水松散层下开采引起饱和土体固结变形的原因和因素,土体在应力、变形变化情况下超静孔隙水压力的消散问题;陈允芳[26]在煤矿开采沉陷研究中考虑了地层疏水作用,并提出了采煤与地下水疏降共同作用下的地表沉陷计算模型与控制理论,但上述研究中所考虑的地层疏水沉降多限于浅部潜水地层疏水,对深部高承压水的疏水沉降研究较少[27-28]。
综上可见,针对厚松散层薄基岩且底部含水层直覆基岩开采条件,分析开采引起的底含疏水与固结受力变形机制,构建厚松散层薄基岩开采地表沉陷预计模型,开展厚松散层底部承压含水层渗流-力场耦合作用下,开采工作面覆岩移动与底含疏水固结沉降双介质上覆地层沉降移动规律研究,对科学留设类似条件工广保护煤柱,确保工广立井井筒与建筑(构)物安全,具有重要理论意义与应用价值。
1 厚松散层底含直覆薄基岩开采地表沉陷预计模型
1.1 厚松散层底含直覆薄基岩开采覆岩移动机理
理论研究和生产实践表明,煤层开采引起的地表沉陷是一个极其复杂的地层移动过程,主要取决于煤层厚度、开采方式、上覆岩层特性等条件。对于薄松散层条件开采,地表沉陷主要由工作面上覆基岩移动造成,可视为单一介质开采沉陷问题,煤层开采引起的上覆基岩移动是地表沉陷的惟一控制源函数。
厚松散层底含直覆薄基岩条件煤层开采,底含承压水易通过断层、原(次)生裂隙向采空区上覆岩层中离层空间或井下疏排,形成以采空区为中心的水位降落漏斗,进而导致厚松散层底含发生压缩沉降。因此,该类条件下的地表沉降,是采区覆岩移动和厚松散层底含疏水固结沉降共同作用的结果,也是其主控源函数的最主要的2个影响因素(图1)。
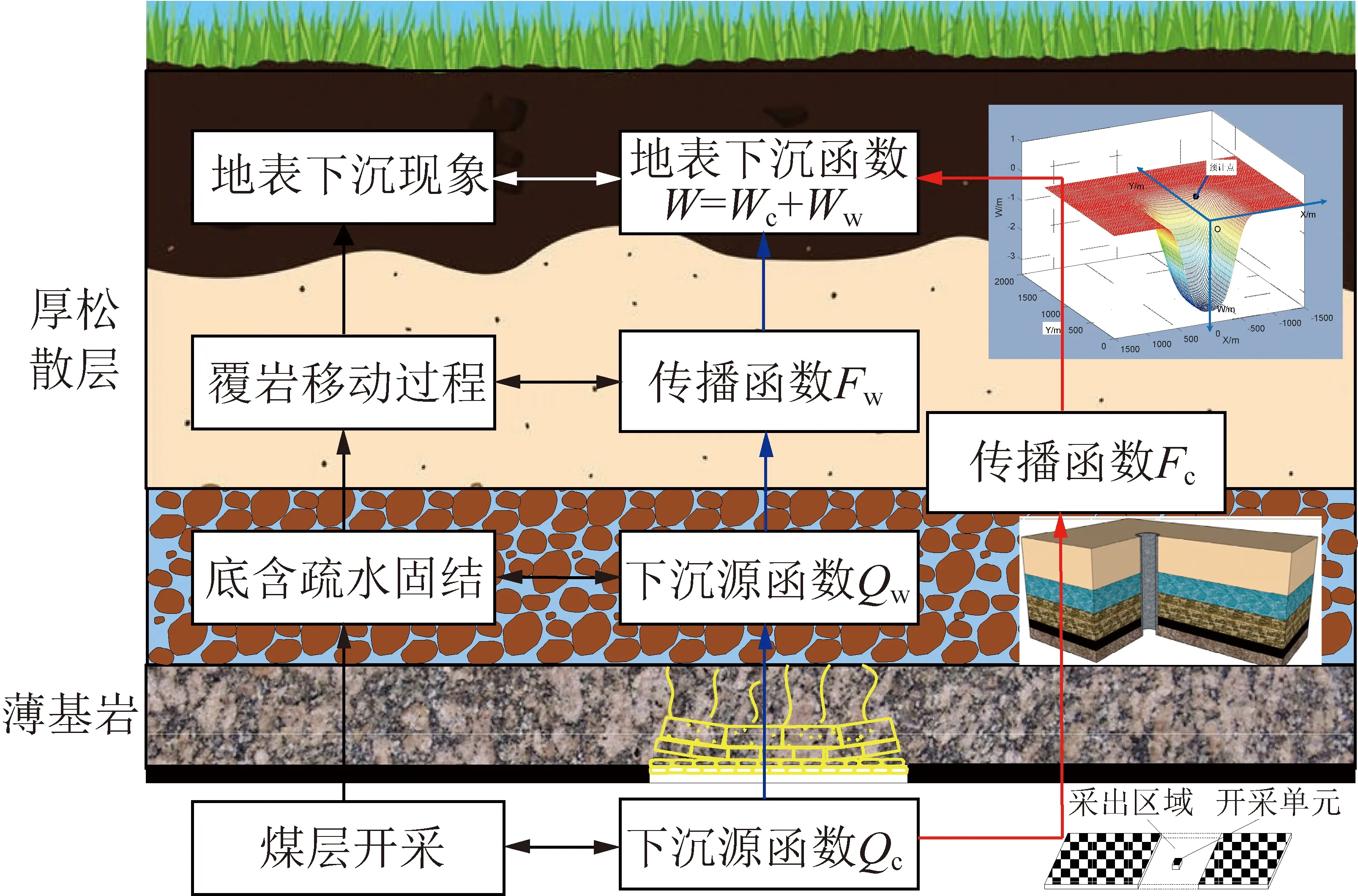
图1 厚松散层底含直覆薄基岩开采覆岩移动机理示意Fig.1 Schematic diagram of overburden movement mechanism in mining when the bottom aquifer of thick loose layer directly covers thin bedrock
1.2 基本假设
为建立该地质条件下开采沉陷预计模型,将厚松散层薄基岩开采地表沉陷模型分为煤层开采沉陷和底含水疏降固结沉陷2部分,并作出如下假设:
(1)煤层开采满足传统概率积分法沉陷模型;
(2)底含为水平均质、各向同性的固液两相随机介质,疏降造成的孔隙压缩仅沿z向发生;
(3)地表沉降与底含降落漏斗、单独采煤作用地层下沉中心在地表水平面投影重合。
1.3 采煤和底含疏降水共同作用地表沉陷预计模型
由模型基本假设,建立的厚松散层底含直覆薄基岩开采地表沉陷模型如图2所示。选择走向采空区中央正上方的地表点O作为横坐标轴x的原点,由原点沿水平面指向煤层走向方向为x轴正向;地表横坐标为x的任意点下沉量W(x)和水平移动量U(x)分别由原点O竖直向下和竖直向上。
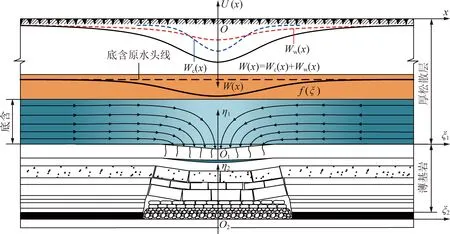
Wc(x),Ww(x)分别为采煤和底含疏降水时的地表下沉量图2 采煤与底含疏降水共同作用地表沉陷模型Fig.2 Surface subsidence model under combined action of coal mining and dewatering of bottom aquifer
同时,分别设置一个煤层坐标系统和底含疏水固结坐标系统,其坐标原点分别在走向采空区底板中点O2和走向采空区底板中点正上方的厚松散层底含底部O1,横坐标ξ1和ξ2与x轴方向相同,纵坐标η1和η2竖直向上,3个坐标系统的比例尺相同,相应三维坐标系统与图2坐标系符合右手定则。由此,采煤和底含承压水疏降引起的地表沉陷为2个沉陷事件线性叠加的结果,即
(1)
2 地表沉陷预计模型求解
2.1 底含疏水固结引起的地表移动及变形求解
2.1.1 底含疏水固结沉降机理
底含承压水发生疏降后,底含中原先由孔隙承压水所分担的应力向固相土粒转移,导致有效应力增加,底含发生固结压密。由于底含在疏水范围内不同位置处的水头下降不同,其孔压消散速度和消散量各异,进而引起上覆松散层发生非均匀沉降。
由工程渗流力学可知,底含水疏降引发的地表下沉量Ww(x)可表示为
(2)
式中,Qw(ξ1,η1)为底含下沉源函数;Fw(x,ξ1,η1)为下沉传播分布函数;Ω1为底含水疏降区域;dS为面积积分符号。
2.1.2 底含疏水固结求解
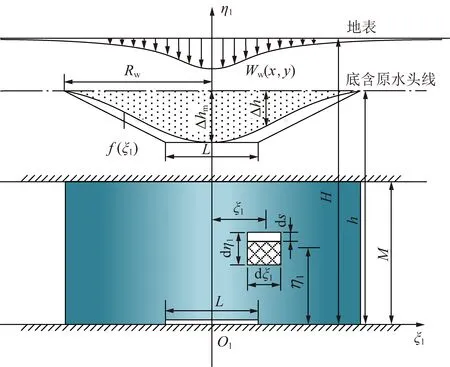
由模型基本假设(2),设(H-h)为疏水前底含土体中地下水水位(图3),其底含各点水头均为h(以底含底部为水头基准面,并忽略地下水流动产生的流速水头),并将η1=M以上多层含、隔水层松散层土体等效为均质土体,η1=M以下为饱和承压均质土体。
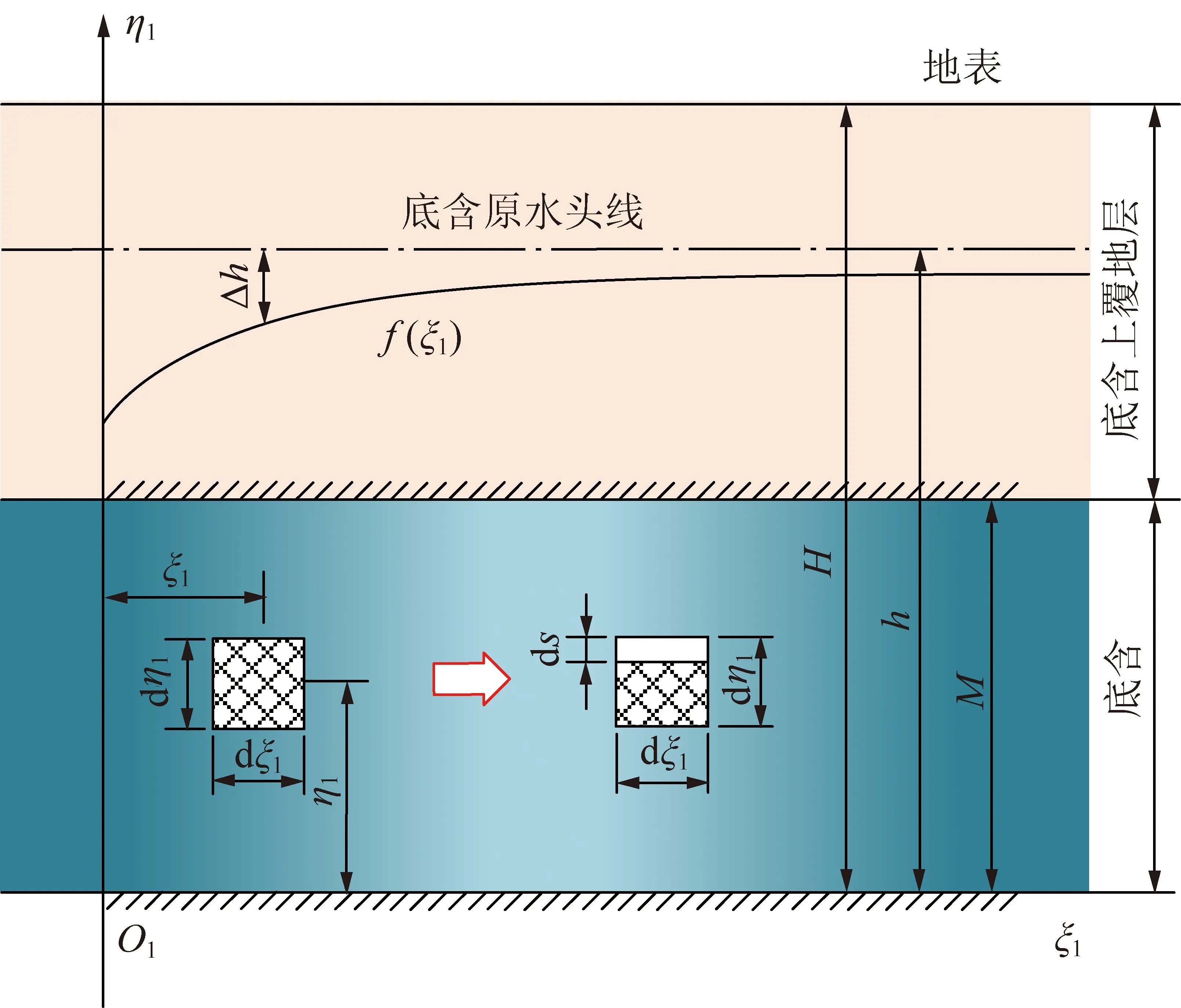
图3 底含疏水固结Fig.3 Drainage consolidation of bottom aquifer
考虑位于深度(H-η1)处的二维平面单元dξ1dη1,单元所受总应力为p,内部孔隙水压力为pw,固相土粒间的有效应力为σ,则底含疏水前各应力表达式为
p=(H-M)γ0+(M-η1)γf
(3)
pw=(h-η1)γw
(4)
σ=(H-M)γ0+(M-η1)γf-(h-η1)γw
(5)
式中,γ0为底含上覆地层平均容重,kN/m3;γf为底含饱和土体容重,kN/m3;γw为孔隙水容重,kN/m3。
由土力学有效应力基本原理可知,底含的压缩变形与孔隙度的变化主要受有效应力σ影响,pw属于各向等压应力,当p恒定时,pw的变化将直接引起σ的改变。若底含底部发生疏降水,水头下降Δh,由于上覆总应力保持恒定,孔隙水压力降低的部分转化为由固相土粒承担,故有
p=(pw-Δhγw)+(σ+Δhγw)
(6)
由土的压密系数公式和固结公式,可得位于深度(H-η1)处的二维平面单元dξ1dη1在Δσ作用下产生的微元固结压缩量ds,其压缩量函数即二维平面模型的下沉源函数Qw(ξ1,η1),可表示为
(7)
式中,e0为底含初始孔隙比;Δe为底含孔隙比的变化;av为底含压密系数。
当Δσ相当大时,压密曲线e-lgσ近似为一直线,压缩指数Cc可表示为
(8)
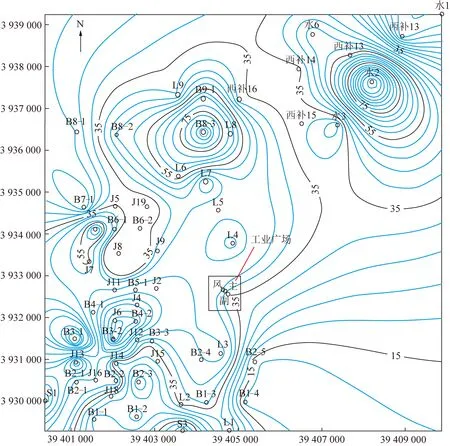
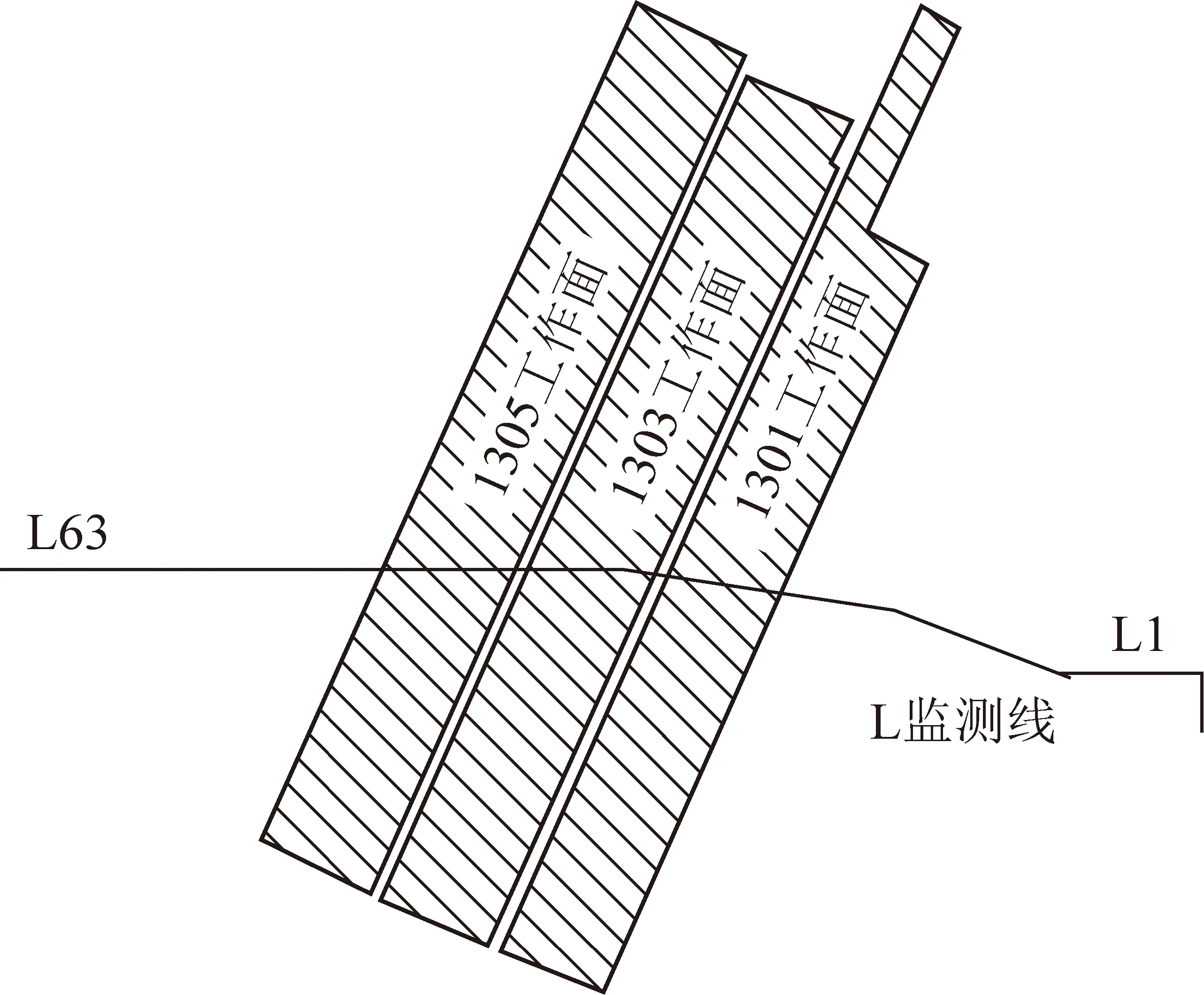
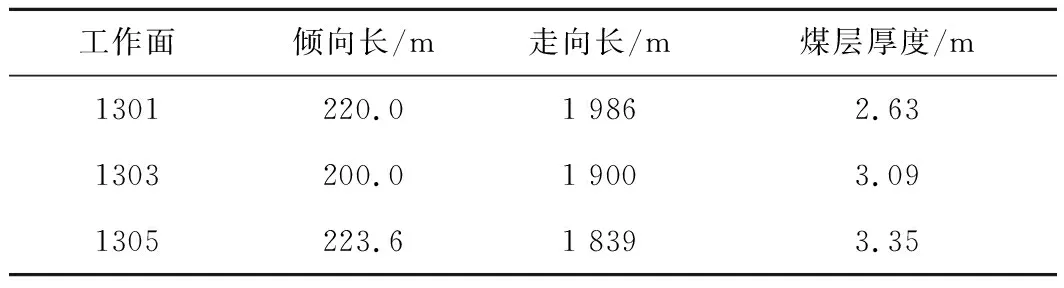
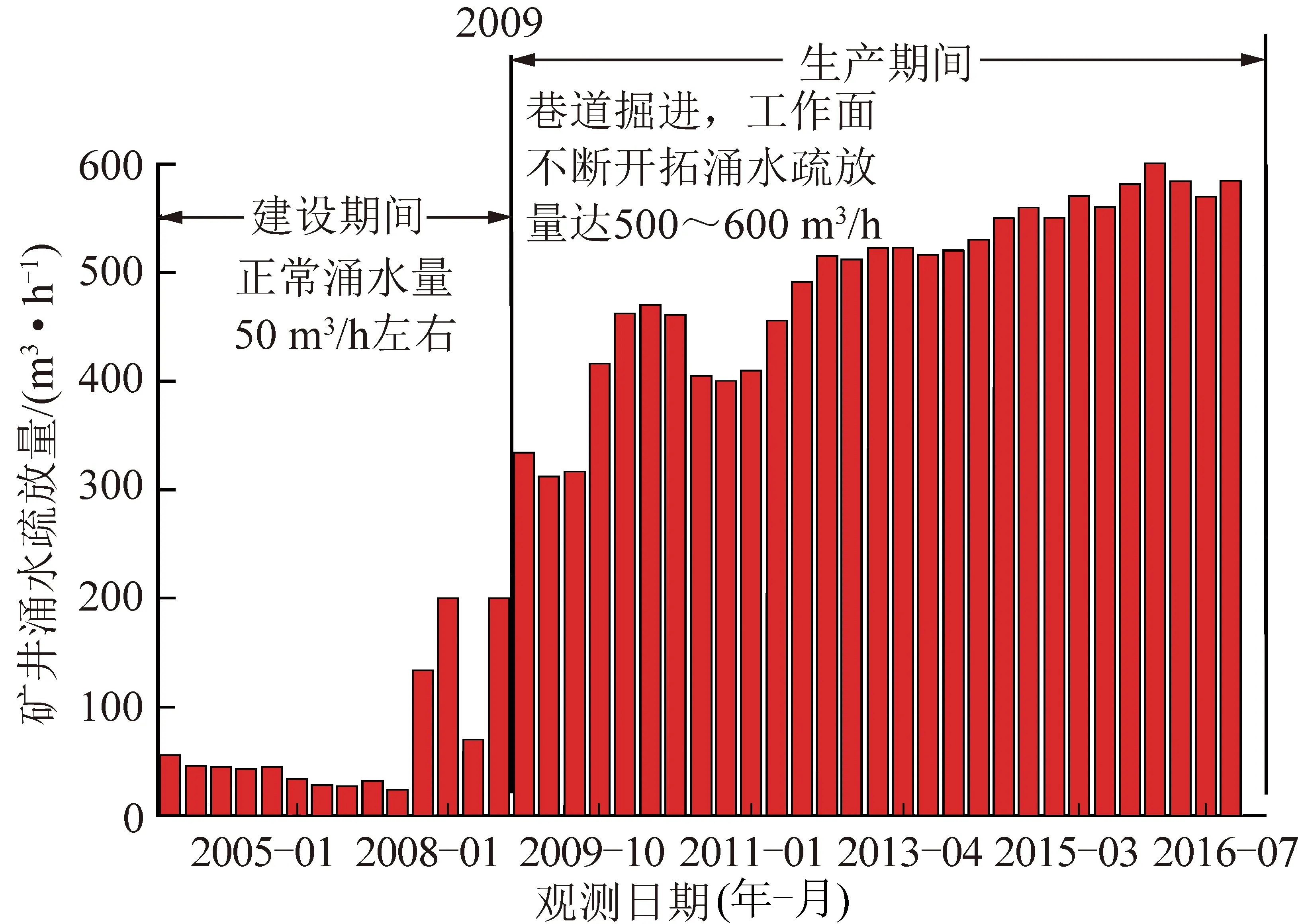
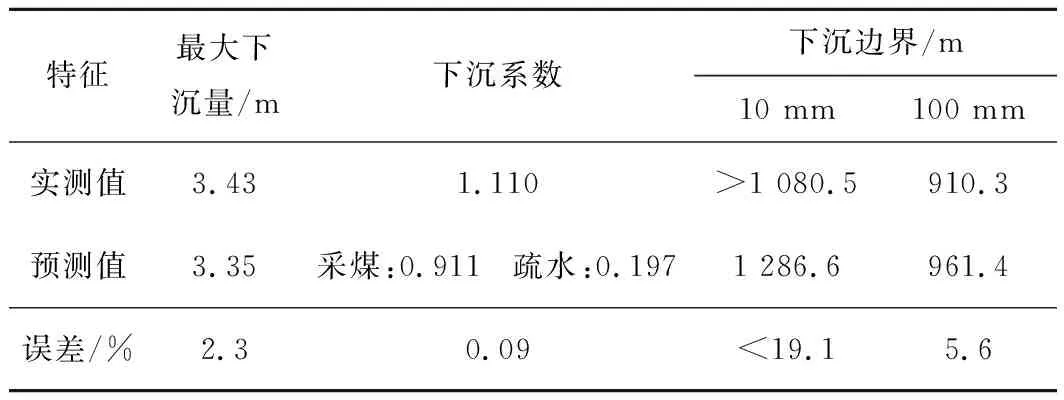
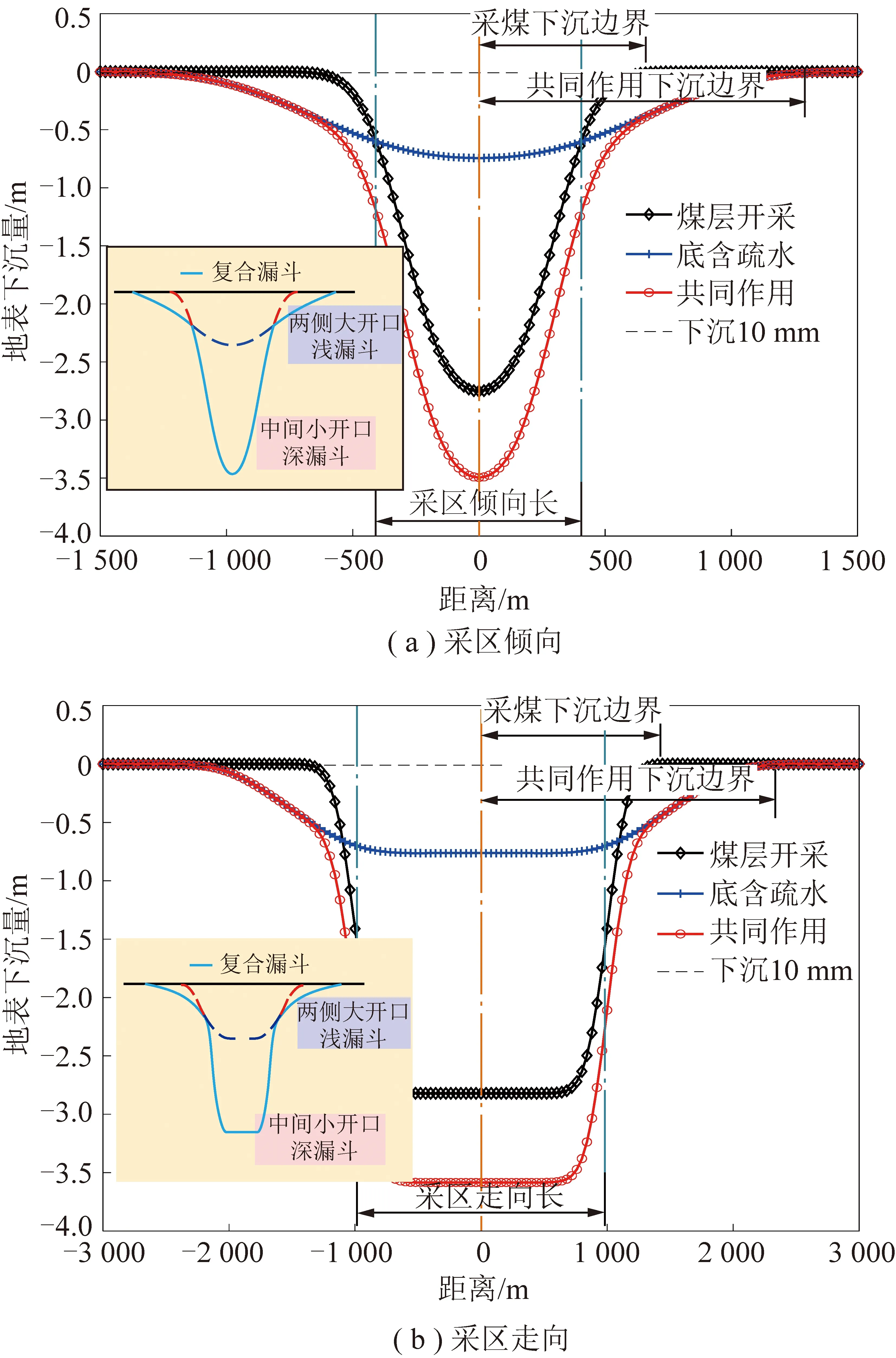
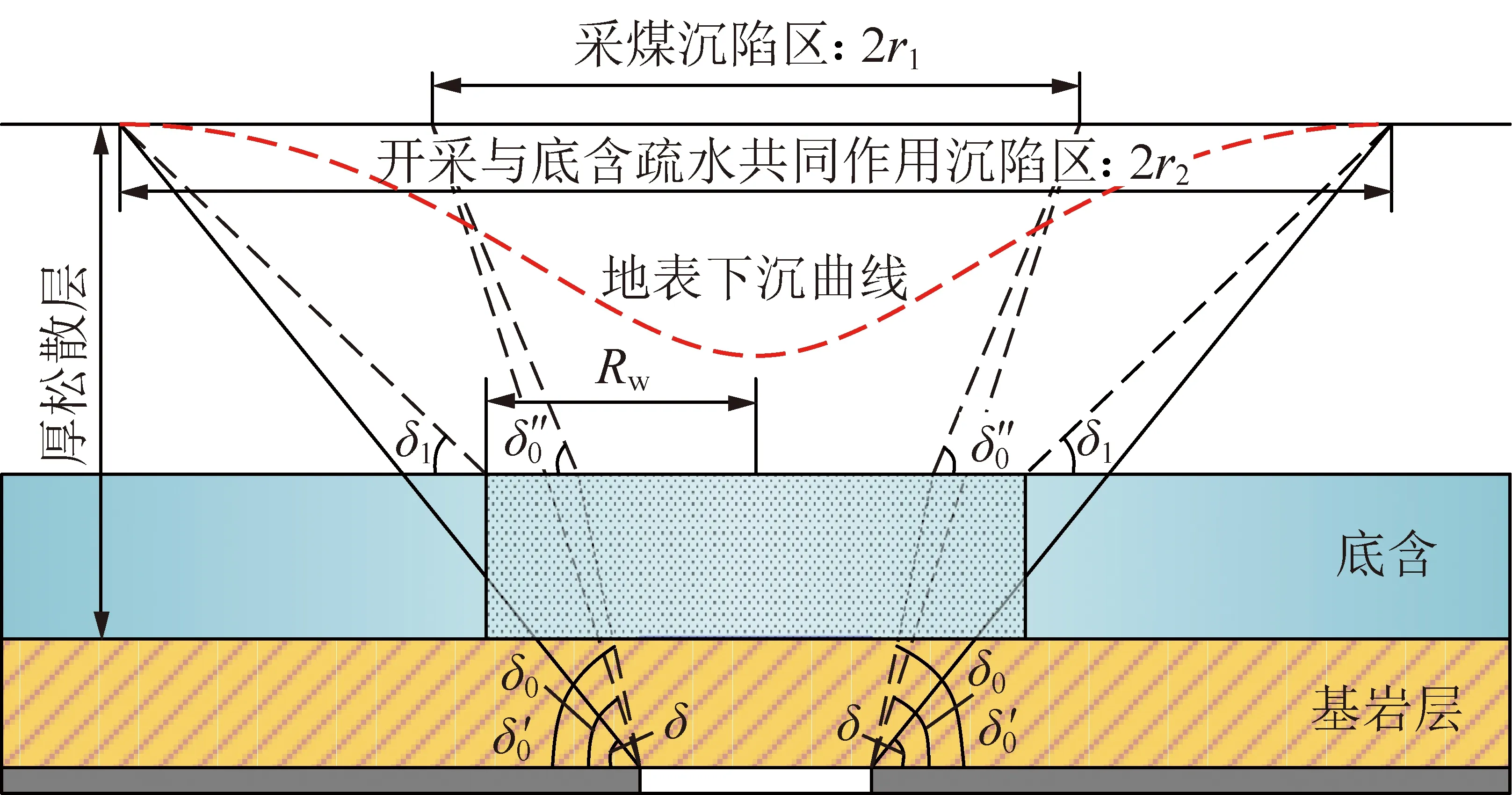
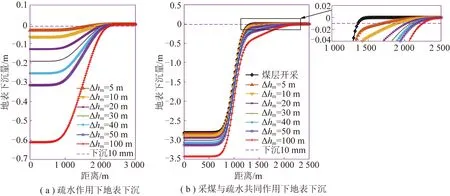
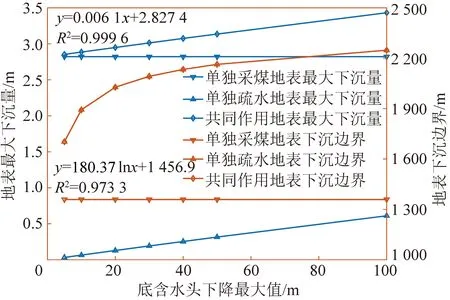
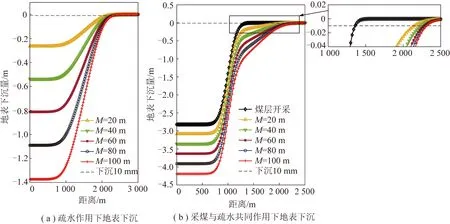
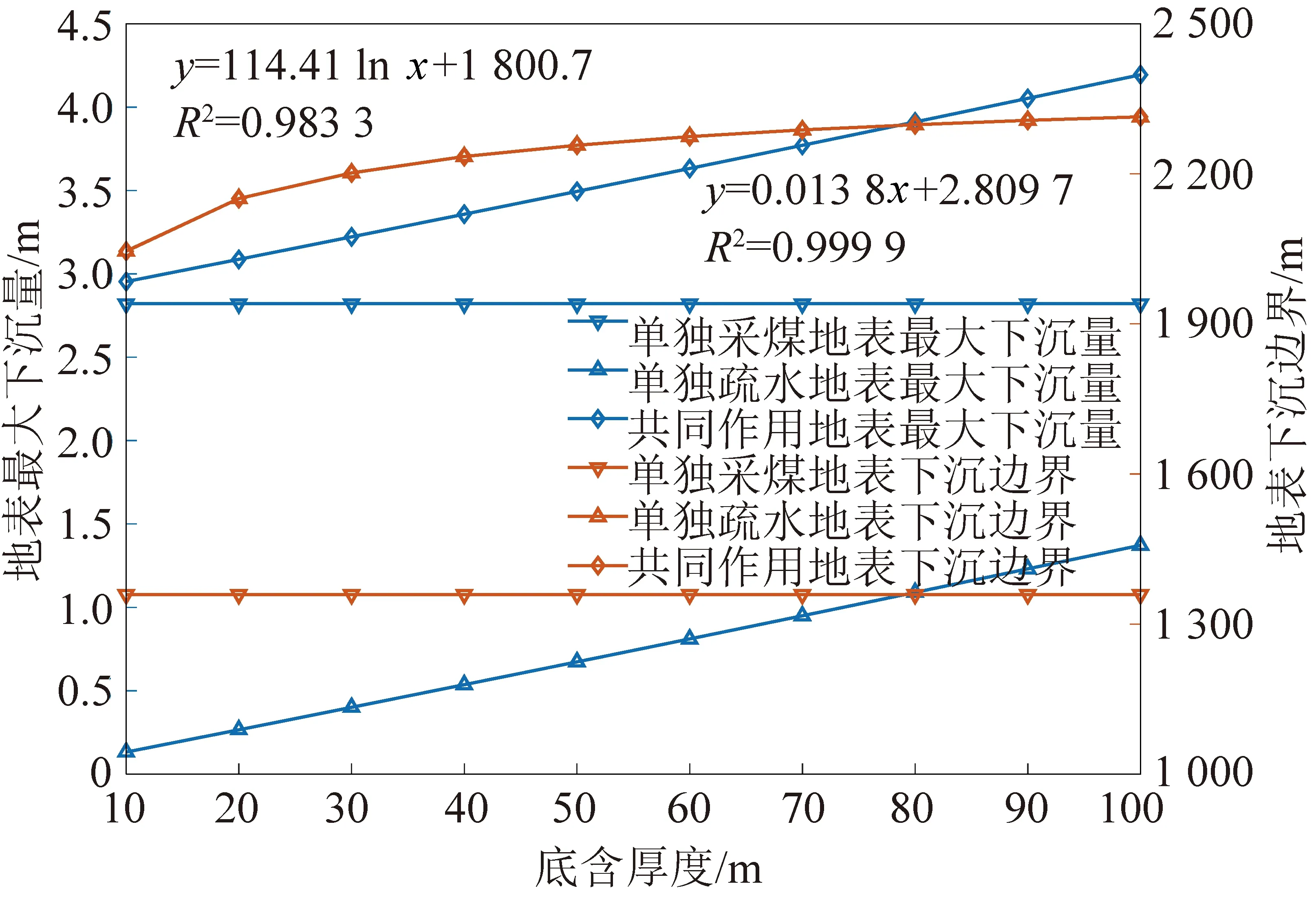
一般认为,Cc≤0.2时为低压缩土;0.2 因此下沉源函数Qw(ξ1,η1)可表示为 (9) 可写成 Qw(ξ1,η1)=ds=C(η1)dη1 (10) 其中, 2.1.3 底含疏水固结引起的地表移动求解 图4为煤层走向主断面上覆厚松散层底含水疏降引起的地表沉降二维平面模型。由图4可见,疏水前底含承压水水位为(H-h),疏水后水位下降Δh,其疏水后底含水水位曲线为f(ξ1),影响半径为Rw。 图4 底含疏降引起的地表沉降模型Fig.4 Surface subsidence model caused by bottom aquifer dewatering 由模型基本假设(2)可知,底含疏水固结压缩ds,可等效为深度(H-η1)处dξ1×ds(宽度×厚度)的煤层开采。由于底含及其上覆松散层满足随机介质理论,在底含疏水固结压缩ds的影响下,η1水平以上的地层将依次下沉,最终在地表形成单元下沉盆地Wwe(x),由底含虚拟降落漏斗范围内疏水固结引起的地表下沉为底含不同位置处单元疏水固结压缩下沉的传播叠加。 根据随机介质理论,二维平面问题中底含单元疏水固结压缩下沉引起的地表下沉即底含疏降水造成的地表下沉传播分布函数,即 (11) 式中,r(η1)为η1水平上底含疏水固结对地表沉降的主要影响范围。 (12) 式中,β1为底含疏水沉降的主要影响范围角。 在底含顶部η1=M与底含底部η1=0之间的整个底含疏水影响半径范围±Rw内,任何疏水固结单元均产生微小体积压缩dξ1ds,由式(10)得 dξ1ds=C(η1)dξ1dη1 (13) 将底含虚拟降落漏斗范围内疏水引起的地层压缩看作变厚开采,地表由于底含疏水固结产生的最终下沉量Ww(x)即上述微元体影响的叠加: (14) 将式(10)~(13)代入式(14),可得底含疏水引起的地表沉降为 (15) 图4中底含疏水后水位降落漏斗分布特征曲线f(ξ1)一般可通过水文孔水位监测或裘布依公式计算获得。 根据采煤工作面上覆松散层水文观测孔底含水位疏降规律,在实际应用中可用分段函数代替疏水后底含水水位曲线f(ξ1)。其中,工作面正上方基岩顶面水头下降相同,等效为一水平直线;工作面边界±L/2至疏水影响边界±Rw之间水头线性降低,等效为一斜直线。这样底含水头下降分布就变成等腰梯形。故此可得到走向主断面上各点的水头下降值为 (16) 式中,Δhm为底含降落漏斗中心处最大水头下降值。 综合上述推导,可得底含走向主断面疏降水造成的地表沉降最终表示为 Ww(x)=Ww1(x)+Ww2(x)+Ww3(x) (17) 式中, 图5 底含疏水沉降引起的地表三维沉降坐标系Fig.5 Three dimensional coordinate system of surface subsidence caused by hydrophobic settlement of bottom aquifer (18) 则底含η1水平处某一三维单元B(ξ1,ζ1,η1)的疏水固结引起地表任意点A(x,y)的下沉Wwe(x,y)可表示为 (19) 则在底含顶部η1=M与底含底部η1=0之间的整个底含疏水影响半径范围±Rw内,任何疏水固结单元均产生微小体积压缩dξ1dζ1ds,地表因底含疏水产生的最终下沉量Ww(x,y)即上述微元体影响的叠加: (20) 将微元固结压缩量ds=C(η1)dη1代入式(20),即可得到地表任意点因底含疏水产生的最终沉降表达式: (21) 由文献[29],二维情况下单元煤层开采引起地表任意点A(x,y)的下沉Wce(x)为 (22) 式中,r为煤层开采沉陷主要开采影响半径。 同样,将二维坐标系统扩展为三维坐标系统,若煤层是水平的,煤层坐标系ξ,o2,ζ和地表坐标系x,o,y水平投影重合,则单元煤层B(ξ,ζ)的开采引起地表任意点A(x,y)的下沉Wce(x,y)为 (23) 在倾斜煤层中,煤层顶板最大下沉量为W0=mqcosα,即采厚按照W0计算,则在整个开采范围Ω内采煤引起地表A(x,y)点的下沉为 (24) 以郭屯煤矿1301,1303,1305工作面为工程背景,验证上节提出的采煤和底含疏降水共同作用地表沉陷预计模型的正确性。该矿上述3个工作面上覆新生界第三系和第四系松散层平均厚度585 m左右,基岩段以泥岩、粉砂岩为主,平均厚度260 m,属典型厚松散层薄基岩地质条件。区域内新生界含水层自上而下分为3个含水层(组)和2个隔水层(组)。第三含水层又称“底含”,其厚度为35~120 m(图6)。 (1)仅使用基本的角点探测器是不够的。例如,与图像之间的跟踪和匹配相比,角点的“种类”并不是很重要,对角点探测器影响较大的因素主要由建筑物的边缘形状和纹理角。 图6 郭屯煤矿松散层底含厚度[30]Fig.6 Bottom aquifer thickness of loose layer in Guotun Coal Mine[30] 该底含下部无隔水层,直接覆盖在基岩风氧化带之上,底含与二叠系石盒子组砂岩裂隙含水层存在水力联系,为基岩裂隙含水层的主要补给水源[10]。 据统计,郭屯煤矿自建井至2016年7月,矿井水疏放量从50 ~ 60 m3/h 增至500 ~ 600 m3/h;至2017年底,底含水位已由-6.35 m降至-203.45 m(图7)。该矿在多个采煤工作面上方地表共建立了15条观测线。其中,观测线中L线点L1~L70横跨1301,1303,1305,1307工作面,从2012年1月14日开始沉降监测到2015年10月20日,获取了1301,1303,1305工作面接近充分采动引起的地表动态沉陷数据,其开采情况见表1、图8。 图8 L线监测点布设示意Fig.8 Layout of L-line monitoring points 表1 1301,1303,1305工作面开采情况Table 1 Mining conditions of working faces 1301,1303 and 1305 图7 矿区涌水量统计柱状图Fig.7 Statistical column chart of water inflow in mining area 根据1301,1303,1305工作面上覆地层钻孔资料、水文孔监测数据及首采1302工作面开采沉陷预计参数反演结果,可得3个工作面开采及其上覆底含疏水沉降综合计算参数:煤层平均厚度3.02 m,开采深度840 m,上覆松散层厚度587.4 m,底含厚45.4 m,工作面沿测点L1~L63(倾向)长644 m;煤层开采下沉系数q=0.8,主要影响角正切tanβ=2.5;底含水疏降前水位为-300 m,疏水固结主要影响角正切tanβ1=1,初始孔隙比e0=0.55,底含承压水以上土体平均容重γ0=17 kN/m3,底含承压水中饱和土体容重γf=19 kN/m3,孔隙水容重γw=9.81 kN/m3。 为简化计算,将1301,1303,1305三个工作面开采对底含疏水影响效应简化为一个等效降落漏斗。根据该矿及其邻近类似矿井底含疏水资料,取底含疏水影响半径Rw=1 000 m,工作面上覆底含最大水头下降值Δhm=100 m,综合走向长取600 m,可得底含主断面上疏水影响半径内各点的水头下降值为 (25) 根据上述参数及本文推导的地表沉陷预计模型,采用Matlab数值计算软件编程计算,可得该矿1301,1303,1305工作面开采及其上覆底含疏水固结共同作用下沿煤层倾向地表沉陷结果,如图9所示。 图9 地表沉陷实测值与本模型理论值对比Fig.9 Comparison between the measured value of surface subsidence and the theoretical value calculated by this model 由表2可知,本文推导的地表沉陷预计模型理论计算所得地表最大下沉量、下沉系数、地表下沉100 mm的边界点距离分别为3.35,1.109,961.4 m;与实测值相对误差分别为2.3%,0.09%,5.6%。由图10可见,采用采煤与疏水共同作用的煤层开采地表沉陷预计模型计算绘制的沉陷曲线与实测资料高度吻合,由此验证了第2节提出的预计模型的正确性。 表2 地表沉陷实测值与本模型理论值对比结果Table 2 Comparison results between the measured value of surface subsidence and the theoretical value calculated by this model 图10 采煤和底含疏降水共同作用地表沉陷特征曲线Fig.10 Characteristic curve of surface subsidence under combined action of coal mining and dewatering of bottom aquifer 以郭屯矿为案例,采用第1节提出的采煤和底含疏降水共同作用地表沉陷预计模型,分析采煤和底含疏降水共同作用地表沉陷特征及其主要影响因素。 分析图10底含水位疏降100 m时采区倾向和走向地表沉陷特征曲线可知,厚松散层薄基岩且“底含”直覆基岩条件下,采煤和底含疏降水共同作用地表沉陷特征与单独开采沉降有较大区别。 底含疏水沉降后,地表下沉盆地中心处沉降量显著增加,导致下沉系数大于1,且地表下沉10 mm边界点明显向采区外侧延伸。 以采区走向充分开采沉陷为例,单独煤层开采产生的地表沉陷曲线呈典型“小开口盆地”型。由于底含的疏水固结作用,增加了盆地中心位置的地表下沉量,减缓了盆地边缘的收敛速度,使得采煤与疏水共同作用下地表下沉盆地呈明显“中间小开口深,两侧大开口浅盆地”复合型特征,下称“复合盆地”。究其原因,厚松散层薄基岩底含疏水固结沉降,一方面加大了沉陷盆地中部的沉降量,另一方面也大幅增加了地表下沉和水平移动范围。 图11 地表移动盆地边界角Fig.11 Boundary angle of ground subsidence trough (26) 式中,r1为采煤作用地表沉陷范围;Hbr为基岩层厚度;δ0为采煤作用地表移动盆地边界角,其值一般大于45°[14]。 由图11可得,受底含疏水固结沉降作用,地表移动范围显著增加,下沉盆地边缘收敛速度降低,疏水沉降盆地边界角δ1为 (27) 其中,r2为开采与底含疏水共同作用地表沉陷范围。由图10可知,采煤和底含疏降水共同作用地表沉陷范围常与底含疏水沉陷范围相近,据此,共同作用下地表移动盆地边界角δ满足: (28) 分析可得,该工况下单独煤层开采时地表移动盆地边界角δ0=66.9°,共同作用下边界角δ=39.7°,底含疏水固结作用大幅增加了地表下沉范围。 为探讨该模型参数体系下厚松散层底含疏水对地表沉陷变形的影响,以采区走向充分开采沉陷为例,分别对底含最大水头下降值Δhm、疏水影响半径Rw和底含厚度M三个因素在不同工况下分析底含疏水对地表沉陷变形的影响。 4.2.1 底含水位下降 最大水头下降值Δhm分别取5,10,20,30,40,50,100 m时地表沉陷特征曲线,如图12所示。 图12 地表沉陷与最大水头下降值的关系Fig.12 Relationship between surface subsidence and maximum waterhead drop value 由图12分析可知,Rw和M恒定时,Δhm主要影响地表沉陷程度,地表下沉10 mm的边界点向采区外侧延伸不明显。随着Δhm增加,底含疏水作用产生的地表“大开口盆地”型沉陷曲线逐渐由“大开口浅盆地”型演化为“大开口深盆地”型,其开口尺寸变化较小,“盆地”型深度逐渐增加;采煤与疏水共同作用下地表沉陷曲线形态逐渐由“浅复合盆地”型演化为“深复合盆地”型。 具体的,疏水作用产生的地表最大下沉量以及共同作用下最大下沉量均与Δhm呈较高线性增长关系(R2>0.999),表明开采工作面上覆底含水头下降程度直接影响地表最大下沉量。 底含水头下降100 m引起地表附加下沉0.611 m,导致地表最大下沉量增加近21.7%,显著增大了地表下沉变形量。Rw=1 000 m时,共同作用下的地表下沉边界与单独疏水作用下的地表下沉边界相同,其值随Δhm近似满足对数增长规律(R2>0.97),底含疏水增加了地表下沉范围,但最大水头下降值Δhm的增加对地表下沉范围的增加影响较小,如图13所示。 图13 地表沉陷与最大水头下降值的关系曲线Fig.13 Relationship curve between surface subsidence and maximum waterhead drop value 4.2.2 底含疏水影响半径 底含疏水影响半径Rw分别取1 200,1 400,1 600,1 800,2 000 m,可得不同Rw时地表沉陷特征曲线,如图14所示。 由图14分析可知,M和Δhm恒定时,Rw主要影响地表沉陷范围,地表最大下沉量保持不变。随着Rw增加,底含疏水作用产生的地表“盆地”型沉陷曲线开口尺寸不断增加,而“盆地”型深度不变,其形态逐渐由“小开口浅盆地”型演化为“大开口浅盆地”型;采煤与疏水共同作用下地表沉陷曲线形态逐渐由“小开口深复合盆地”型演化为“大开口深复合盆地”型,表现为地表最大下沉量保持不变,而其下沉10 mm的边界点向采区外侧急剧延伸。 图14 地表沉陷与疏水影响半径的关系Fig.14 Relationship between surface subsidence and hydrophobic influence radius 具体的,当Rw=1 000 m时,地表下沉边界受底含疏水和采煤共同影响;当Rw>1 200 m时,地表下沉边界仅受底含疏水影响,其下沉边界与底含疏水引起的地表下沉边界相同,且其值随Rw呈线性增长关系。当Rw=0(底含不疏水)时,地表下沉10 mm边界为1 359 m;当Rw=1 000 m时,下沉边界增加至1 485 m;当Rw=2 000 m时,增加至2 248 m,相对Rw=0时增加了65.4%,相对于Rw=1 000 m时增加了51.4%,表明底含疏水增加了地表下沉范围,且随着Rw增加而急剧增加。在厚松散层底含疏水作用下,地表沉陷范围远大于一般单独采煤地表沉陷范围(图15)。 图15 地表沉陷与疏水影响半径的关系曲线Fig.15 Relationship curves between surface subsidence and hydrophobic influence radius 4.2.3 底含厚度 底含厚度M分别取20,40,60,80,100 m,可得不同M时地表沉陷特征,如图16所示。 图16 地表沉陷与底含厚度的关系Fig.16 Relationship between surface subsidence and bottom aquifer thickness 由图16,17分析可知,Rw和Δhm恒定时,底含厚度M对地表沉陷的影响规律与Δhm对地表沉陷的影响规律相似,M主要影响地表沉陷程度,地表下沉10 mm的边界点向采区外侧延伸不明显。随着M增加,底含疏水作用产生的地表“大开口盆地”型沉陷曲线逐渐由“大开口浅盆地”型演化为“大开口深盆地”型,其开口尺寸变化较小,“盆地”型深度逐渐增加;采煤与疏水共同作用下地表沉陷曲线形态逐渐由“浅复合盆地”型演化为“深复合盆地”型。 图17 地表沉陷与底含厚度的关系曲线Fig.17 Relationship curve between surface subsidence and bottom aquifer thickness 我国目前大多数矿区均采用由刘宝琛、廖国华教授在J·李特威尼申提出的随机介质理论基础上建立的概率积分法来预计采动地表沉降,该预计模型因模型参数易确定、预测精度高和能与计算机编程软件有机结合等优点被广泛应用,但随着我国浅部煤炭资源逐渐枯竭,开采逐渐向深部进行,该模型预测精度及实用性逐渐降低。究其原因,是由于概率积分法将上覆松散层和基岩层视为同一介质,不能考虑2种介质物理力学参数差异,致使预测值和实际监测值之间出现误差,当松散层厚度逐渐增大时,这种误差也被放大,尤其是厚松散层开采地表沉降盆地边缘区域的预测精度差。因此,传统概率积分法主要适用于薄(无)松散层厚基岩地质条件下的采动地表沉陷预计。 针对厚松散层采动地表沉陷预计问题,国内外专家学者在传统概率积分法基础上,提出了改进的预计模型,主要有基于岩层控制关键层理论的“类双曲线”移动模型[31]、上位松散层随机介质—下位基岩均质连续各向同性弹性体(梁弯曲)的双层介质力学模型[17,32]、基于关键层托板理论的上位岩土层—巨厚松散层的随机介质和下位岩层—关键层层状介质的复合介质模型[33]、上部松散随机介质—中部弹性薄板—下部离散介质的复合介质耦合模型[34]等,这类模型综合考虑了松散层和基岩层之间力学特性、变形特性及地层厚度的差异,并将两者视为不同的介质,同时考虑了关键层对地表沉降的影响,针对厚松散层采动地表沉陷预测精度相对于传统概率积分法有了较大提高。但由于改进的预计模型主要是从力学角度建立的,尚未考虑松散层底部含水层疏水固结影响,因此针对厚松散层底含直覆薄基岩采动条件下的地表沉降预计,上述模型的适用性需进一步研究探讨。鉴于此,笔者综合考虑煤层开采和底含疏水固结对地层移动变形的综合影响,根据叠加原理建立厚松散层底含直覆薄基岩采动地表沉降预计模型,在沉陷盆地中部及边缘区域预测精度均得到较大提升,且模型适用性更加广泛。 (1)厚松散层底含直覆薄基岩条件下,开采产生的裂隙带会波及至松散层与基岩交界面,形成底含疏水通道,引发其疏水固结沉降。针对该类地质条件,提出的开采沉陷预计模型考虑了松散层底含疏水固结沉降对开采沉陷特征的重要影响,并得到工程验证。 (2)由于厚松散层薄基岩底含疏水固结沉降作用,加大了沉陷盆地中部的沉降量,大幅增加了地表下沉和水平移动的范围,出现下沉系数大于1,且地表下沉10 mm边界点明显向采区外侧延伸现象。其地表沉陷曲线呈“中间小开口深盆地,两侧大开口浅盆地”型。 (3)采区走向充分开采沉陷时,最大水头下降值Δhm与地表最大下沉量呈正相关,但对沉陷范围影响较小;底含疏水影响半径Rw主要影响地表沉陷范围,对地表最大下沉量无影响;底含厚度M主要影响地表沉陷程度,对沉陷范围影响不大。 (4)厚松散层底含直覆薄基岩条件下,煤层开采易发生“底含”疏水固结沉降,大幅加大地表沉降量和沉陷范围。建议针对该类地层,适时修改现行的《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》(2017版)有关条款,以确保地面及工广内建(构)物,特别是井筒安全。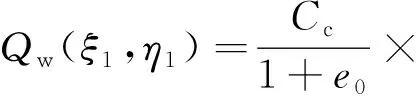
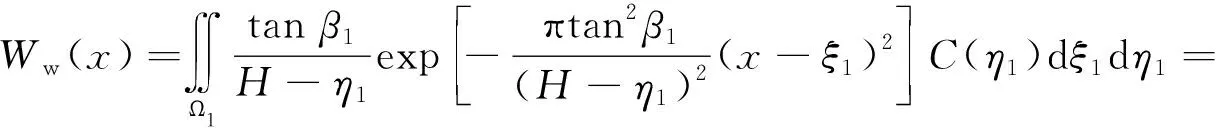
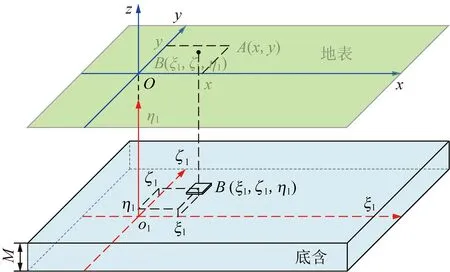
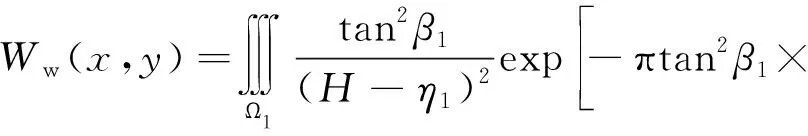
2.2 采煤引起的厚松散层薄基岩沉降计算
3 模型验证
3.1 工程背景
3.2 模型验证

4 讨 论
4.1 沉降特征
4.2 主要影响因素


4.3 厚松散层地表沉陷模型适用性分析
5 结 论

