基于GA-BP神经网络的喷丸样品表层硬度预测模型

石明，汪舟,2，甘进，杨莹,2，王晓丽,2，任旭东，申建国，邱斌

表面强化技术

基于GA-BP神经网络的喷丸样品表层硬度预测模型

石明1，汪舟1,2，甘进3，杨莹1,2，王晓丽1,2，任旭东1，申建国1，邱斌4

（1.武汉理工大学 a.汽车工程学院 b.现代汽车零部件技术湖北省重点实验室，武汉 430070；2.汽车零部件技术湖北省协同创新中心，武汉 430070；3.武汉理工大学 交通学院，武汉 430063;4.中国汽车工程研究院股份有限公司，重庆 401122）

建立能够准确预测不同喷丸工艺参数下工件表层显微硬度的数学模型。以42CrMo钢作为研究对象，采用正交实验法设计喷丸实验方案和逐点测量法测量0～320 μm层深内的显微硬度，以实验数据为样本，基于BP神经网络建立42CrMo钢受喷后表层显微硬度的预测模型，并利用遗传算法（GA）对BP神经网络结构进行优化，建立基于GA-BP神经网络的42CrMo钢受喷后表层显微硬度模型。将实验数据集用于模型的训练，BP神经网络模型和GA-BP神经网络模型训练的相关系数均为0.97左右，两种模型的训练效果均较好。对比20组测试集的模型预测值和实验值发现，BP神经网络模型预测值与实验值之间的相对误差的最大值和平均值分别为3.5%和1.1%，相比之下，经遗传算法优化的BP神经网络（GA-BP）模型预测值与实验值的相对误差的最大值和平均值仅为2.9%和0.7%。GA-BP神经网络模型具有更高的预测精度和稳定性。经GA遗传算法优化的BP神经网络（GA-BP）更适合用于建立受喷工件表层显微硬度的预测模型，可为其在工程上的应用提供一定的参考。

喷丸强化；显微硬度；神经网络；遗传算法优化；预测模型

喷丸强化作为一种机械表面强化工艺，其通过改善金属材料的表面完整性（表面纹理和表面层冶金质量），从而显著提高机械零部件的抗疲劳强度和疲劳寿命[1-3]，因此目前被广泛应用于各工业领域[4-6]。喷丸处理通过大量的球形弹丸反复撞击零部件表面，使零件表层材料发生塑性变形，在零件表层引入残余压应力场的同时使表层产生加工硬化，表层组织晶粒细化，从而使得表层硬度增大[7-8]。这种由于喷丸引起的组织结构变化也被证实和残余压应力场一样，对于提高金属零部件的疲劳寿命有着显著的影响[9-10]。

目前国内外对喷丸引起的表层组织结构变化和表层硬度变化进行了大量的实验研究。Wang等人[11]和Ahmed等人[12]的研究表明，经喷丸强化后的金属部件表层组织晶粒细化，表层的显微硬度也显著提高。Iida等人[13]研究发现相比于玻璃丸，使用铸钢丸进行喷丸处理后的工件，其表面残余压应力和表面硬度更大。Xie等人[14]通过实验获得了经喷丸处理后钛合金不同层深下的显微硬度，并总结了喷丸后钛合金显微硬度沿层深方向梯度变化的规律。目前在喷丸领域获取零件喷丸后硬度沿层深分布的主要方式是通过硬度仪逐点测试，这种方式通常会耗费测试人员大量的时间，特别是对于获取大量不同工艺参数下受喷零部件的表层显微硬度分布，这种测量方式需要耗费大量的时间和人力成本。神经网络作为目前较为流行的一种算法数学模型，被证实具有强大的非线性映射能力和自学习能力，其非常适合用于求解内部机制复杂的问题，从而对相关结果进行合理地预测，而且相比于传统实验具有明显的成本优势，因此被广泛应用于各领域[15-16]。目前通过神经网络对喷丸强化的研究主要集中在残余应力场和表面粗糙度方面。Maleki等人[17]研究了喷丸工艺参数对中碳钢表面残余应力、微晶尺寸和半高宽的影响，并通过神经网络建立了它们之间的预测模型。Wang等人[18]利用BP神经网络建立了喷射压力、扫描速度、喷丸距离与工件表面粗糙度之间的预测模型，徐戊矫等人[19]利用BP神经网络建立了初始粗糙度、喷丸直径、喷丸速度、覆盖率与工件表面粗糙度之间的预测模型，通过少量的实验数据进行训练后，模型均被验证了具有良好的预测精度。吴少杰等人[20]利用GA-BP神经网络建立了喷丸表面完整性参数预测模型，基于该模型预测的残余应力和表面粗糙度与实验值的相对误差均小于7%。苏凯新等人[21]对比了GA-BP神经网络、BP神经网络和RBF神经网络预测喷丸后25CrMo钢疲劳寿命的能力，发现经遗传算法优化的BP神经网络（GA-BP）的预测精度最高，基于该模型还成功预测了喷丸后25CrMo钢表面残余压应力的松弛行为。相比于运用神经网络对喷丸后表面残余应力和表面粗糙度等方面的研究，关于神经网络应用于喷丸后表层显微硬度方面的研究较少[22]。

为了减少样品显微硬度测试数据点的同时准确预测不同工艺参数下经喷丸处理后样品沿层深显微硬度分布，本文基于MATLAB建立喷丸工艺参数与显微硬度的神经网络预测模型，选择高强钢42CrMo为研究对象，通过正交实验设计实验方案，对其进行喷丸强化处理，比较BP神经网络模型、GA-BP神经网络模型对喷丸后表层显微硬度预测的优劣性，并给予量化评判。

1 实验方法

选用调质42CrMo钢作为实验材料，其化学成分如表1所示。热处理工艺为850 ℃淬火20 min，然后回火至650 ℃并保温2 h，最后空冷至室温。热处理后，42CrMo钢的初始屈服强度约为680 MPa，抗拉强度约为930 MPa，硬度约为230HV。

表1 42CrMo钢的化学成分

Tab.1 Chemical composition of 42CrMo steel wt.%

采用XN-9065P型气动式喷丸机对42CrMo钢样品进行喷丸强化处理，样品尺寸为3 cm×3 cm×2 cm，弹丸材料为铸钢丸，硬度为45～48HRC。由于喷丸处理涉及诸多工艺参数[23]，为了研究多个工艺参数对显微硬度的影响，采取三因素三水平正交实验法设计实验方案。喷丸工艺正交实验因素水平如表2所示。由于喷丸实验过程中喷丸速度无法直接测量，喷丸速度根据Klemenz[24]推导的经验公式（1）得到。

式中，为喷丸速度（m/s），为喷丸压力（pa），为丸料进给流量（kg/min），为弹丸直径（mm）。

表2 喷丸正交实验因素水平

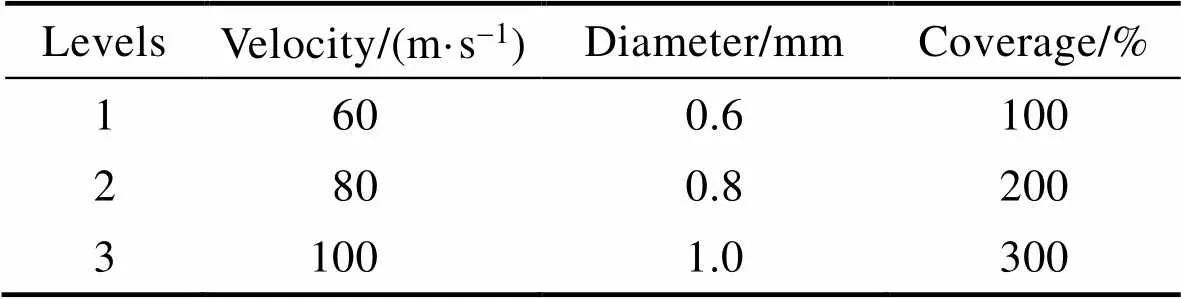
Tab.2 Orthogonal experimental factors for shot peening

42CrMo钢样品经过喷丸处理后，为了便于测量显微硬度，通过线切割的方式从3 cm×3 cm×2 cm的样品上切取10 mm×10 mm×4 mm的小块样品，利用镶嵌机镶嵌在黑色圆柱块内，然后使用砂纸对切割面研磨至1200目，并使用绒布进行抛光处理，如图1所示。通过HV-1000A显微硬度测量仪，在500 g的加载载荷和10 s的保荷时间下，测量距42CrMo钢样品表层0～320 μm的显微硬度。由于受喷表面凹凸不平且被嵌入黑色圆柱块内，导致最表层的显微硬度不便于测量；同时两个相邻测量点之间应保持30 μm以上的距离，以避免上一次测量对下一次测量产生影响[22]。因此，将距受喷表面40 μm左右的层深处作为第一个测量点，然后沿层深方向每隔40 μm测量一次，共测量8个数据点并将其作为一组数据。在正交实验设计的9次实验中，每次实验均测量两组数据，最后获得144个显微硬度数据。

图1 42CrMo钢样品

2 数学模型

2.1 BP神经网络模型

BP神经网络是一种按误差反向传播算法训练的前向神经网络，一般由输入层、隐含层和输出层组成，其数学模型可由式（2）—（3）描述。理论证明3层的神经网络能逼近任意的非线性映射关系[25-26]，因此本文采用3层神经网络结构。典型的3层BP神经网络结构如图2所示。将喷丸速度、弹丸直径、喷丸覆盖率和距喷丸表面距离作为BP神经网络的输入参数，显微硬度作为BP神经网络的输出参数，因此模型的输入层节点数为4，输出层节点数为1，隐含层的节点数根据经验公式（4）确定[27]。

图2 喷丸硬度预测BP神经网络结构

BP神经网络模型的建立主要为训练和测试两个过程。在创建并训练BP神经网络模型之前，首先利用randperm函数从实验测量得到的144组数据中随机划分数据集，这样可以保证数据集样本具有普适性[20]。同时在训练前利用mapminmax函数对所有数据进行归一化处理，以提高网络模型的收敛速度，测试结束后再利用mapminmax函数对数据进行反归一化处理，得到实际值。

2.2 GA-BP神经网络模型

针对BP神经网络训练过程中容易陷入局部极小值的问题，苏凯新等人[21]通过遗传算法（GA）来优化所建立的BP神经网络的结构，以提高模型的预测精度。因此，本文通过调用北卡罗来纳大学GAOT遗传算法工具箱，对喷丸后42CrMo钢表层显微硬度的BP神经网络预测模型的初始权值和阈值进行优化，建立基于GA-BP神经网络的显微硬度预测模型。遗传算法是一种通过模拟自然进化过程搜索最优解的方法，在遗传算法优化BP神经网络结构过程中，其以BP神经网络模型预测值和实际值之间的误差平方和的倒数作为适应度函数，如式（5）所示。对待优化个体进行编码并对种群初始化，随后通过选择、交叉、变异不断迭代优化后，得到最优的初始权值和阈值，然后利用优化的权值和阈值重新训练模型，最终得到经遗传算法优化的BP（GA-BP）神经网络模型预测值。

3 结果与分析

基于MATLAB建立喷丸后42CrMo钢表层显微硬度BP神经网络模型，隐含层和输出层的传递函数分别采用双曲正切tansig函数和purelin线性函数，训练算法采用Levenberg-Marquardt （LM）算法的trainlm函数。性能评价函数采用均方根误差MSE，训练目标误差为0.0001，最大训练次数为5000次，学习速率为0.01。通过randperm函数随机选取124组数据为BP和GA-BP神经网络模型的训练集，其余20组数据为这两个模型的测试集。根据经验公式（4），确定隐含层节点个数范围为[3,13]，为了确定最合适的隐含层节点个数，将20组测试集的模型仿真结果与实验结果之间相对误差的平均值（平均相对误差）作为模型训练效果的评价指标。由于数据集的随机划分与神经网络初始权值和阈值分配的不同，可能会导致在相同的隐含层节点数下，模型的训练结果也会产生一定的偏差，因此对上述范围内每个隐含层节点数下的BP神经网络模型进行多次训练并对结果取平均值，最后再比较不同隐含层节点数下的模型训练效果。如图3所示，图中的柱状图为每个隐含层节点数下的3次模型训练中20组测试集仿真结果与实验结果的平均相对误差，折线图为3个平均相对误差的平均值。从图3中可以看出，当隐含层节点数为8时，模型无论是稳定性还是精度都最佳，说明此时的模型训练效果最好，因此确定喷丸后42CrMo钢表层显微硬度BP神经网络预测模型的网络结构为4-8-1。

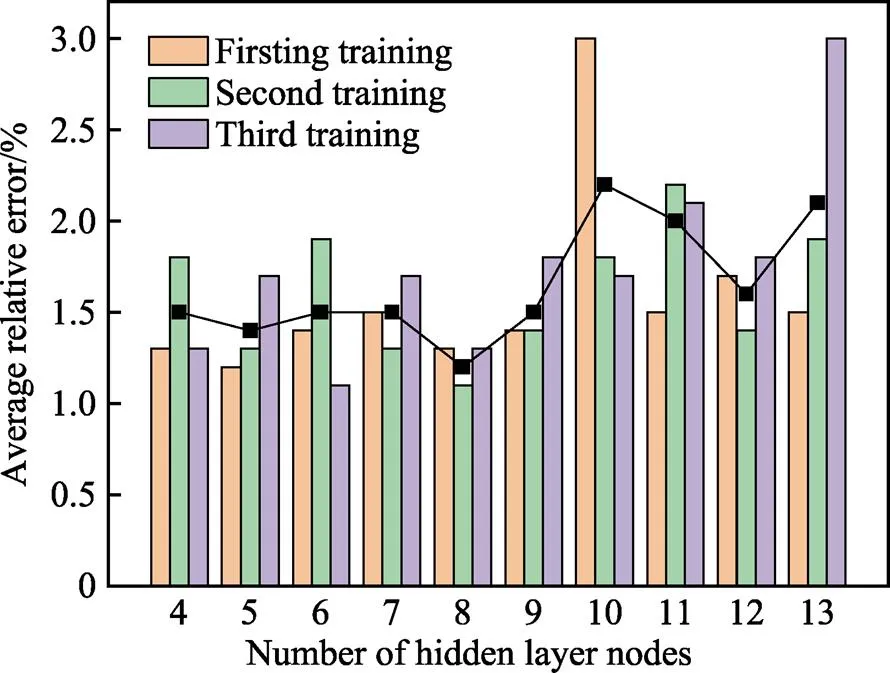
图3 不同隐含层节点数下的模型训练效果

图4为BP神经网络模型训练的回归分析图。从图4中可以看出，数据点基本上分布在回归线附近，而回归系数值越接近1，模型效果越好，因此相关系数=0.970 03表明训练好的模型具有良好的预测精度。将训练好的BP神经网络模型用于预测喷丸后的42CrMo钢表层显微硬度，并将预测的显微硬度值与测量的实验值进行比较，如表3所示。从表3中可以看出，BP神经网络预测的显微硬度值和实验测量值之间的相对误差最大值为3.5%，20组数据相对误差的平均值为1.1%。这表明BP神经网络模型对喷丸后42CrMo钢表层显微硬度具有良好的预测精度。

图4 喷丸后42CrMo钢表层显微硬度BP神经网络模型训练回归分析图

表3 喷丸后42CrMo钢显微硬度的BP神经网络模型的预测值和实验值

Tab.3 Comparison of experimental value and the predicted value of BP neural network model of 42CrMo steel microhardness after shot peening

在基于遗传算法优化的BP神经网络（GA-BP神经网络）模型中，BP神经网络模型参数设置与前文一致；在遗传算法优化网络结构中，种群规模为50，最大迭代次数为100，选择、交叉、变异操作分别调用GAOT工具箱中的normGeomSelect、arithXover和nonUnifMutation函数来实现。图5a为GA-BP神经网络模型的训练回归分析图。可以看出，数据点基本上分布在回归线附近，而回归系数值越接近1，模型效果越好，相关系数=0.967 72同样表明训练好的模型具有良好的预测精度。图5b为GA-BP神经网络模型中遗传算法优化个体的适应度变化曲线，其中红线表示平均个体的适应度随迭代次数的变化曲线，蓝线表示最优个体的适应度随迭代次数的变化曲线。从图5b可以看出，最优个体的适应度和平均个体的适应度均在迭代50次后达到最大值并趋于稳定，由于本文将模型预测值与实际值间的误差平方和的倒数作为适应度值，这表明此时的误差平方和最小，GA-BP神经网络模型的网络结构达到最优，该模型可以用于训练。

图5 喷丸后42CrMo钢表层显微硬度GA-BP神经网络模型

将训练好的GA-BP神经网络模型用于预测喷丸后的42CrMo钢表层显微硬度，并将预测的显微硬度值与测量的实验值进行比较，如表4所示。从表4中可以看出，GA-BP神经网络模型预测的显微硬度值和实验测量值之间的相对误差最大值为2.9%，20组数据相对误差的平均值为0.7%。这表明GA-BP神经网络模型对喷丸后42CrMo钢表层显微硬度同样具有非常高的预测精度。同时对比表4和表3可以发现，通过遗传算法优化BP神经网络结构，可以一定程度上提高神经网络模型的预测精度。虽然在某些工艺参数和层深下，BP神经网络模型预测的显微硬度值比GA-BP神经网络模型预测的更接近实验测量值，但是20组验证数据的统计表明，无论是相对误差的最大值还是20组数据相对误差的平均值，GA-BP神经网络模型预测的误差更小且预测精度更高，这也表明GA-BP神经网络模型相比于BP神经网络模型具有更高的精度和稳定性。另外，从表4中还可以看出，在不同的喷丸工艺参数下，42CrMo钢表层的显微硬度均有一定程度的提高，这是因为在大量弹丸的高速冲击下，42CrMo钢表层材料发生严重的塑性变形，表层组织晶粒细化，从而提高了表层显微硬度。与此同时，对比第1组和第13组数据可以发现，随着喷丸强度的提高，表层组织晶粒细化加剧，同一层深下的显微硬度更大；对比第2组、第12组和第13组数据可以发现，在相同的喷丸工艺参数下，随着层深的增大，材料晶粒尺寸逐渐趋于基体尺寸，显微硬度呈沿层深方向逐渐减小的趋势。

表4 喷丸后42CrMo钢显微硬度的GA-BP神经网络模型的预测值和实验值

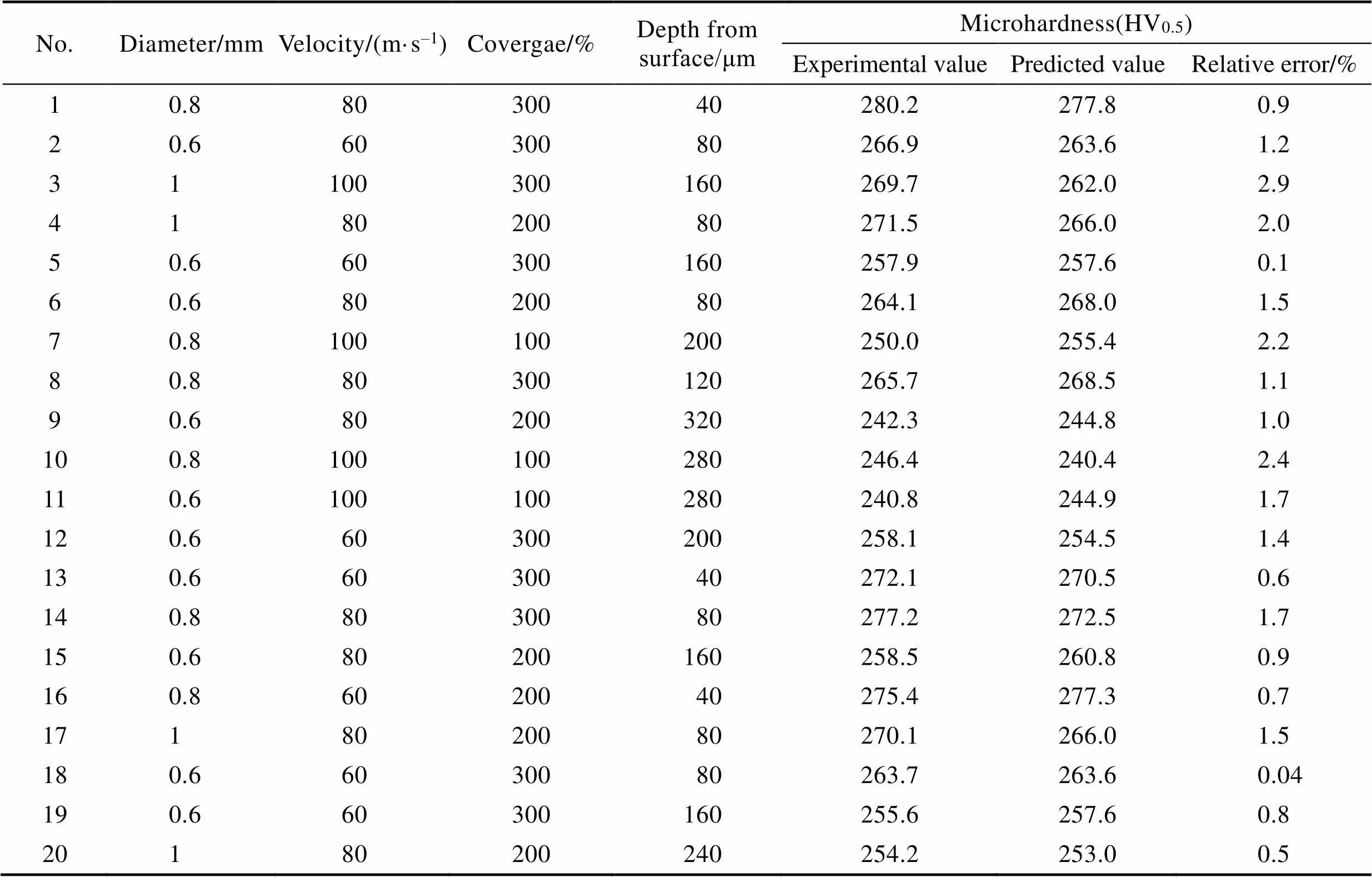
Tab.4 Comparison of experimental value and the predicted value of GA-BP neural network model of 42CrMo steel microhardness after shot peening

4 结论

本文以42CrMo钢作为研究对象，通过正交实验法设计喷丸实验方案，利用较少的实验次数获得一些42CrMo钢表层显微硬度值，并以此为数据样本，基于BP神经网络和经遗传算法优化的BP神经网络（GA-BP神经网络），分别建立了喷丸后工件表层显微硬度沿层深分布的预测模型，并对两种模型进行了比较。得到如下结论：

1）BP神经网络和GA-BP神经网络均可用于建立受喷工件表层显微硬度的预测模型，且两种模型的预测精度良好，可以为其在工程上的应用提供一定的参考。

2）相比于BP神经网络模型预测值与实验值之间的相对误差最大值为3.5%和20组相对误差平均值为1.1%，经遗传算法优化的BP神经网络（GA-BP）模型预测值与实验值的相对误差最大值和20组相对误差平均值分别仅为2.9%和0.7%，这表明GA-BP神经网络模型具有更高的预测精度和稳定性。

[1] 高玉魁. 表面完整性理论与应用[M]. 北京: 化学工业出版社, 2014.

GAO Yu-kui. Theory and Application of Surface Int­egrity[M]. Beijing: Chemical Industry Press, 2014.

[2] 方博武. 受控喷丸与残余应力理论[M]. 济南: 山东科学技术出版社, 1991.

FANG Bo-wu. Controlled Shot Peening and Residual Stress Theory[M]. Jinan: Shandong Science & Techn­ology Press, 1991.

[3] GAO Y, LU F, YAO M. Influence of Mechanical Surface Treatments on Fatigue Property of 30CrMnSiNi2A Steel[J]. Surface Engineering, 2005, 21(4): 325-328.

[4] NAM Y S, JEON U, YOON H K, et al. Use of Response Surface Methodology for Shot Peening Process Optim­ization of an Aircraft Structural Part[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(9-12): 2967-2981.

[5] SCURACCHIO B G, DE LIMA N B, SCHÖN C G. Role of Residual Stresses Induced by Double Peening on Fatigue Durability of Automotive Leaf Springs[J]. Mat­erials & Design, 2013, 47: 672-676.

[6] DEGUCHI T, MOURI M, HARA J, et al. Fatigue Stre­ngth Improvement for Ship Structures by Ultrasonic Peening[J]. Journal of Marine Science and Technology, 2012, 17(3): 360-369.

[7] 花银群, 陈瑞芳, 杨继昌, 等. 40Cr钢表面激光复合强化机理研究[J]. 中国激光, 2005, 32(10): 1445-1448.

HUA Yin-qun, CHEN Rui-fang, YANG Ji-chang, et al. Study on Experiments and Mechanism of 40Cr Steel Surface by Laser Compound Processing[J]. Chinese Journal of Lasers, 2005, 32(10): 1445-1448.

[8] WANG X Y, LI D Y. Mechanical and Electrochemical Behavior of Nanocrystalline Surface of 304 Stainless Steel[J]. Electrochimica Acta, 2002, 47(24): 3939-3947.

[9] 王仁智. 金属材料的喷丸强化原理及其强化机理综述[J]. 中国表面工程, 2012, 25(6): 1-9.

WANG Ren-zhi. Overview on the Shot Peening Principle and Its Strengshening Mechanisms for Metallic Mate­rials[J]. China Surface Engineering, 2012, 25(6): 1-9.

[10] 钱昂, 金平, 谭晓明, 等. AerMet100钢喷丸强化前后表面完整性及疲劳性能分析[J]. 表面技术, 2019, 48(9): 158-166, 176.

QIAN Ang, JIN Ping, TAN Xiao-ming, et al. Effect of Shot Peening on Surface Integrity and Fatigue Properties of AerMet100 Steel[J]. Surface Technology, 2019, 48(9): 158-166, 176.

[11] WANG Cheng, WANG Long, WANG Xiao-gui, et al. Numerical Study of Grain Refinement Induced by Severe Shot Peening[J]. International Journal of Mechanical Sciences, 2018, 146-147: 280-294.

[12] AHMED A A, MHAEDE M, WOLLMANN M, et al. Effect of Micro Shot Peening on the Mechanical Prope­rties and Corrosion Behavior of Two Microstructure Ti-6Al-4V Alloy[J]. Applied Surface Science, 2016, 363: 50-58.

[13] IIDA K, TOSHA K. Comparison between Steel Shot and Glass Shot on the Peened Surface and the Surface Layer[J]. Journal of the Japan Society for Precision Engineering, 1988, 54(5): 922-927.

[14] XIE Le-chun, WANG Li-qiang, JIANG Chuan-hai, et al. The Variations of Microstructures and Hardness of Titan­ium Matrix Composite (TiB+TiC)/Ti-6Al-4V after Shot Peening[J]. Surface and Coatings Technology, 2014, 244: 69-77.

[15] KONDO R, YAMAKAWA S, MASUOKA Y, et al. Microstructure Recognition Using Convolutional Neural Networks for Prediction of Ionic Conductivity in Cera­mics[J]. Acta Materialia, 2017, 141: 29-38.

[16] KARATAŞ C, SOZEN A, DULEK E. Modelling of Residual Stresses in the Shot Peened Material C-1020 by Artificial Neural Network[J]. Expert Systems With Applications, 2009, 36(2): 3514-3521.

[17] MALEKI E. Modeling of Severe Shot Peening Effects to Obtain Nanocrystalline Surface on Cast Iron Using Artif­icial Neural Network[J]. Materials Today: Proce­edings, 2016, 3(6): 2197-2206.

[18] WANG Rui-hong, WANG Chong, ZHANG Xiao-mei. The Prediction of Shot Peening’s Surface Roughness with Premixed Water Jet Based on Neural Network[J]. Ad­vanced Materials Research, 2010, 136: 172-175.

[19] 徐戊矫, 刘承尚, 鲁鑫垚. 喷丸处理后6061铝合金工件表面粗糙度的模拟计算及预测[J]. 吉林大学学报(工学版), 2019, 49(4): 1280-1287.

XU Wu-jiao, LIU Cheng-shang, LU Xin-yao. Simulation and Prediction of Surface Roughness of 6061 Aluminum Alloy Workpiece after Shot Peening[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(4): 1280-1287.

[20] 吴少杰, 刘怀举, 张仁华, 等. 基于正交实验和数据驱动的喷丸表面完整性参数预测[J]. 表面技术, 2021, 50(4): 86-95.

WU Shao-jie, LIU Huai-ju, ZHANG Ren-hua, et al. Prediction of Surface Integrity Parameters of Shot Pee­ning Based on Orthogonal Experiment and Data-Driven[J]. Surface Technology, 2021, 50(4): 86-95.

[21] 苏凯新, 张继旺, 李行, 等. 基于神经网络的喷丸25CrMo合金疲劳寿命及残余应力松弛行为预测研究[J]. 稀有金属材料与工程, 2020, 49(8): 2697-2705.

SU Kai-xin, ZHANG Ji-wang, LI Hang, et al. Prediction of Fatigue Life and Residual Stress Relaxation Behavior of Shot-Peened 25CrMo Axle Steel Based on Neural Network[J]. Rare Metal Materials and Engineering, 2020, 49(8): 2697-2705.

[22] SUN Li-xing, LI Miao-quan, LI Hui-min. Prediction Model for Surface Layer Microhardness of Processed TC17 via High Energy Shot Peening[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(9): 1956- 1963.

[23] CHEN J S, DESAI D A, HEYNS S P, et al. Literature Review of Numerical Simulation and Optimisation of the Shot Peening Process[J]. Advances in Mechanical Engin­eering, 2019, 11(3): 168.

[24] KLEMENZ M. Anwendung Der Simulation Der Randsc­hichtausbildung Beim Kugelstrahlen Auf Die Absch­ätzung Der Schwingfestigkeit Gekerbter Bau­teile[D]. Baden- Württemberg: der Universität Karlsruhe (TH), 2009

[25] CYBENKO G. Approximation by Superpositions of a Sigmoidal Function[J]. Mathematics of Control, Signals and Systems, 1989, 2(4): 303-314.

[26] HORNIK K, STINCHCOMBE M, WHITE H. Multilayer Feedforward Networks are Universal Approximators[J]. Neural Networks, 1989, 2(5): 359-366.

[27] 王瑞红, 徐洁, 兰翠, 等. Elman神经网络射流喷丸表面粗糙度的预测模型[J]. 黑龙江科技大学学报, 2015, 25(2): 224-228.

WANG Rui-hong, XU Jie, LAN Cui, et al. Prediction Model Tailored for Surface Roughness of Jet Peening Based on Elman Neural Network[J]. Journal of Heilon­gjiang University of Science and Technology, 2015, 25(2): 224-228.

Microhardness Prediction Model of Peened Parts Based on GA-BP Neural Network

1,1,2,3,1,2,1,2,1,1,4

(1. a. School of Automotive Engineering, b. Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology, Wuhan 430070, China; 2. Hubei Collaborative Innovation Center for Automotive Components Technology, Wuhan 430070, China; 3. School of Transportation, Wuhan University of Technology, Wuhan 430063, China; 4. China Automotive Engineering Research Institute Co., Ltd., Chongqing 401122, China)

The work aims to establish a mathematical model that can accurately predict the surface microhardness of peened parts under different shot peening parameters. Taking 42CrMo steel as the research object, the shot peening experiment plan was designed by orthogonal experiment method and the point-by-point measurement method was used to measure the microhardness in the depth of 0～320 μm. The BP neural network was used to establish the surface microhardness prediction model of 42CrMo steel after shot peening. Meanwhile, genetic algorithm (GA) was used to optimize the structure of BP neural network, and the surface microhardness prediction model of 42CrMo steel after shot peening based on GA-BP neural network was established. Velocity, diameter, coverage and depth from surface were set as the input parameters, and the surface microhardness was set as the output parameter in both two models. The experimental data was divided into two parts, where the training set was used for the training of the two models, the correlation coefficientof BP neural network model and GA-BP neural network model was about 0.97, and the training effect of the two models was good. By comparing the predicted value of two models and the experimental value of 20 groups of test set, it was found that the maximum and average relative errors between the predicted value of the BP neural network model and the experimental value were 3.5% and 1.1%, respectively. The maximum and average relative errors between the predicted value of the GA-BP neural network model and the experimental value were only 2.9% and 0.7%, respectively. The GA-BP neural network model had higher prediction accuracy and stability. The BP neural network optimized by genetic algorithm (GA-BP) is more suitable for establishing the prediction model of the surface microhardness of peened parts, which can provide some guidance for the industrial application.

shot peening; surface microhardness;neural network; genetic algorithm; prediction model

2021-02-09；

2021-07-02

SHI Ming (1997—), Male, Postgraduate, Research focus: lightweight of automobile.

汪舟（1981—），男，博士，副教授，研究方向为汽车轻量化、汽车零部件先进制造、多物理场耦合仿真。

Corresponding author：WANG Zhou (1981—), Male, Doctor, Associate professor, Research focus: lightweight of automobile, advanced manufacturing of auto parts, multiphysics coupling simulation.

石明, 汪舟, 甘进, 等. 基于GA-BP神经网络的喷丸样品表层硬度预测模型[J]. 表面技术, 2022, 51(1): 332-338.

TG668

A

1001-3660(2022)01-0332-07

10.16490/j.cnki.issn.1001-3660.2022.01.036

2021-02-09；

2021-07-02

国家自然科学基金（51879208，51405356）

Fund：Supported by the National Natural Science Foundation of China (51879208, 51405356)

石明（1997—），男，硕士研究生，主要研究方向为汽车轻量化。

SHI Ming, WANG Zhou, GAN Jin, et al. Microhardness Prediction Model of Peened Parts Based on GA-BP Neural Network[J]. Surface Technology, 2022, 51(1): 332-338.