基于Matlab的引信探测参数计算程序实现*

裴 喆

（92941部队 葫芦岛 125000）

1 引言

防空导弹经常采用周向探测体制的无线电或激光引信。导弹与目标遭遇时，引信对目标进行探测后引爆战斗部，对目标进行毁伤。引信探测参数包括探测的时间、距离、方位等，对于一次拦截飞行，探测参数是分析引信工作的重要依据。现有方法多在采用三维软件建立目标精细化几何模型的基础上，统计计算引信对每个单位面元的探测参数[1～4]。这类方法中目标三维建模和探测参数计算编程均较为复杂，比较适用于几何外形复杂的飞机类目标。对于几何外形相对简单的导弹类目标，本文基于数学函数丰富、矩阵计算和曲线绘制简便的Matlab软件[5]，设计实现引信探测参数计算程序。

2 引信探测参数计算方法

2.1 引信探测模型

地面坐标系oxyz下反导迎攻拦截条件下弹目遭遇时的引信探测模型如图1所示。

图1中分别以导弹和目标的尾部为原点定义弹体坐标系odxdydzd和目标机体坐标系obxbybzb，F点表示引信在导弹上的位置，引信波束绕弹轴360°形成一个空心圆锥，实现周向探测；波束主瓣倾角Ω定义为引信波束主瓣与弹轴的固定夹角；bj点表示引信探测到目标的任意一点，Rj表示探测距离。

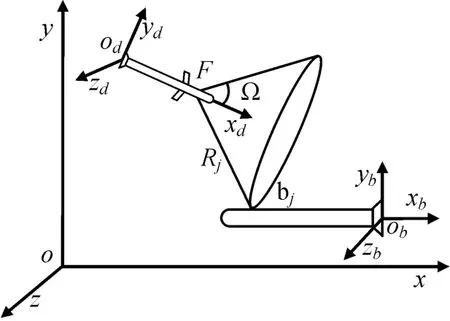
图1 引信探测模型

对于一次弹目遭遇，计算引信探测参数的原理是首先建立目标三维特征点模型，然后对弹目运动测量数据进行拟合处理后计算引信和目标特征点的运动数据，最后根据引信波束窄、探测距离近、波束覆盖区域小的特性[6]，计算探测参数。

2.2 引信探测参数计算方法

2.2.1 建立目标多截面特征点矩阵模型

导弹类目标几何外形通常近似为细长圆柱体，因此可建立多截面的特征点矩阵模型。方法是先在机体坐标系obxbybzb中xb方向均匀选取若干特征点，对于每个xb方向特征点再在其yb、zb方向（即截面周向）均匀选取若干特征点。以某截面为例，其周向特征点坐标可用矩阵bx1表示如下。

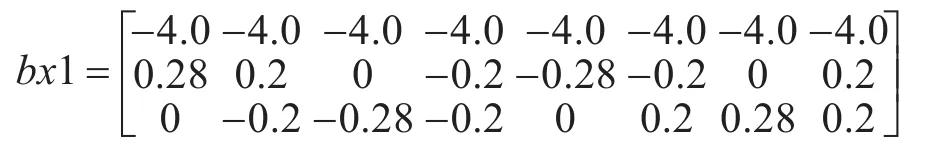
矩阵bx1共8列，表示该截面周向均匀选取的8个特征点；矩阵共3行，第1、2、3行数据分别表示每个特征点的 xb、yb、zb坐标。

2.2.2 弹目运动测量数据拟合处理

这里的弹目运动测量数据是指遭遇段导弹和目标的尾部 od和 ob在地面坐标系oxyz中x、y、z三个方向的运动位置测量数据，分别记为（x（dtT），y（dtT），z（dtT））和（x（btT），y（btT），z（btT））。测量数据总是包含误差的，本文只讨论随机误差，随机误差一般服从均值为零的正态分布[7]。由于弹目遭遇时间很短，可认为弹目均作匀速直线运动[8]。因此可利用最小二乘直线拟合的方法对弹目三维方向测量数据分别进行除差平滑。测量数据时间tT的采样周期较大[9]，为此还需对拟合后的数据在时间上线性插值处理为不大于0.1ms的周期，最后得到的弹目运动数据记为（xd（nt），yd（nt），zd（nt））和（xb（nt），yb（nt），zb（nt））。利用拟合得到的导弹各方向速度（vxd，vyd，vzd）和位移初值（xd0，yd0，zd0），由式（1）可计算（xd（nt），yd（nt），zd（nt））。

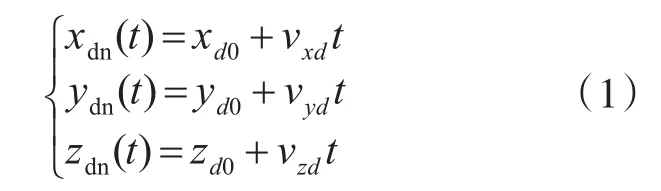
同时可计算导弹弹道偏航角φd和弹道倾角θd。φd定义为导弹速度矢量在xoz平面投影与ox轴的夹角，θd定义为导弹速度矢量与xoz平面的夹角[7]。选取导弹运动数据的任意一点（（xdn（tk），ydn（tk），zdn（tk）），则φd和θd的计算如式（2）和式（3）所示。

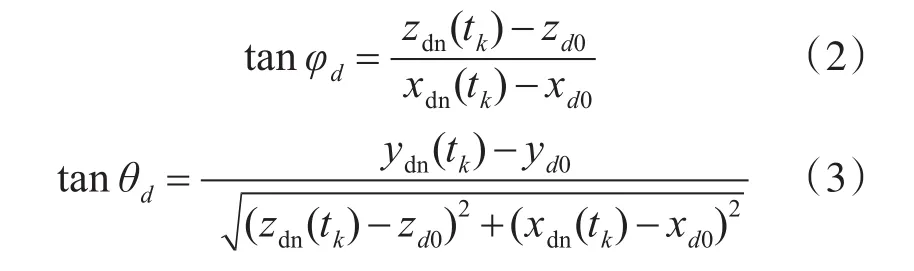
同理，可拟合得到的目标各方向速度（vxb，vyb，vzb）和位移初值（xb0，yb0，zb0）计算（xbn（t），ybn（t），zbn（t））。目标航向角φb和轨迹倾角θb的定义分别与φd和θd类似，因此可同理计算φb和θb。

2.2.3 计算引信和目标特征点的运动数据

1）计算引信运动数据

首先，将引信F点的弹体坐标（xdf，ydf，zdf）转换为地面坐标（xf，yf，zf），计算如式（4）所示[10]：

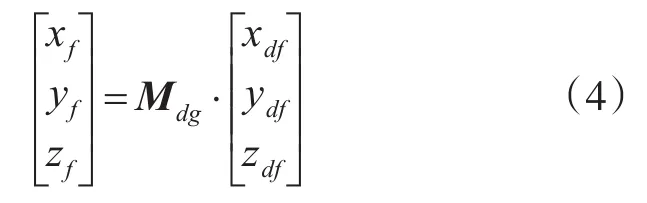
式中，Mdg为导弹弹体坐标系与地面坐标系的转换矩阵。由于防空导弹和导弹类目标结构上均为轴向对称，可不考虑滚动角的影响。因此Mdg利用φd和θd计算得到，具体如式（5）所示[11]：

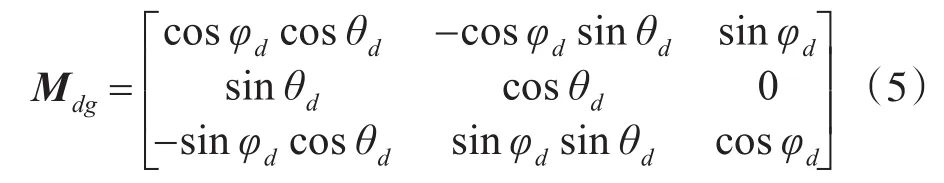
然后，将导弹原点运动数据（xdn（t），ydn（t），zdn（t））与引信坐标（xf，yf，zf）对应相加，即得引信运动数据（xfn（t），yfn（t），zfn（t）），记为直线lf（t）。

2）计算目标特征点的运动数据

任取目标特征点bj（j=1，2，…，n），其机体坐标记为（xbj，ybj，zbj），将其转换为地面坐标（xbj0，ybj0，zbj0），转换公式与式（4）同理。然后，将坐标（xbj0，ybj0，zbj0）与目标原点运动数据（xbn（t），ybn（t），zbn（t））相加，即得特征点bj运动数据（xbjn（t），ybjn（t），zbjn（t）），记为直线lbj（t）。

2.2.4 计算引信探测角

记引信F点和目标特征点bj之间的直线为lfbj（t），其方向数为（mfbj（t），nfbj（t），kfbj（t））。直线lf（t）和直线lfbj（t）的夹角记为Ωfbj（t）。已知直线lf（t）方向数为（vxd，vyd，vzd），则Ωfbj（t）如式（6）所示：

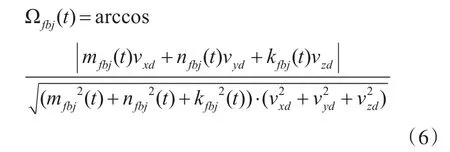
当Ωfbj（tj）=Ω时，Ωfbj（tj）即为引信对特征点bj的探测角，tj即为探测时间。

2.2.5 计算引信对目标的实际探测参数

对于目标机体xb方向每个截面的周向特征点，根据最先探测、时间最早原则确定唯一的实际周向探测点。得到所有截面实际周向探测点探测参数之后，对这些探测参数分别进行xb方向的三次样条插值处理[12]，即可得到引信对目标的实际探测参数。

3 程序运行实例

3.1 弹目参数设置

利用Matlab语言对引信探测参数计算方法进行了程序实现，为验证算法与程序的正确性，设置一组弹目参数，进行实例运行。

设引信波束主瓣倾角Ω=60°，波束宽度2°。目标机体xb方向从头部到尾部每隔0.5m取1个特征点，共取8个（对应8个截面）；对每个截面再每隔45°均匀选取8个周向特征点。

设置一组遭遇段弹目运动真值数据，加入零均值正态分布白噪声，生成模拟的测量数据。

3.2 引信探测参数计算

导入模拟的弹目运动测量数据，运行程序得到拟合后的弹目运动数据三维曲线如图2所示。图中dn表示导弹运动数据，bn表示目标运动数据。由图可知弹目遭遇时导弹在目标的下方。

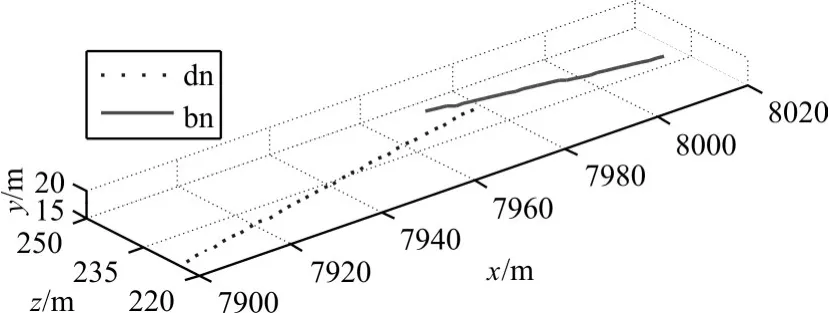
图2 弹目运动数据三维曲线

以目标头部为例，截面周向特征点坐标用矩阵bx1表示，引信对各周向特征点的探测角度、时间计算结果分别如图3和图4所示。图中横坐标表示8个截面周向特征点的方位。

由图3可知引信对各个特征点的探测角度均在波束范围内，由图4可知头部实际周向探测点位于目标下方（方位180°）。

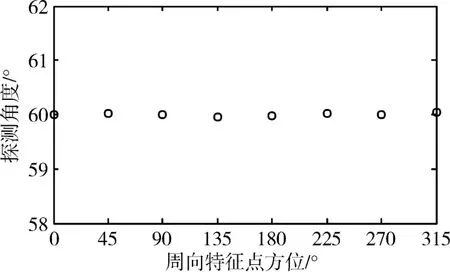
图3 引信对目标头部截面周向特征点探测角度

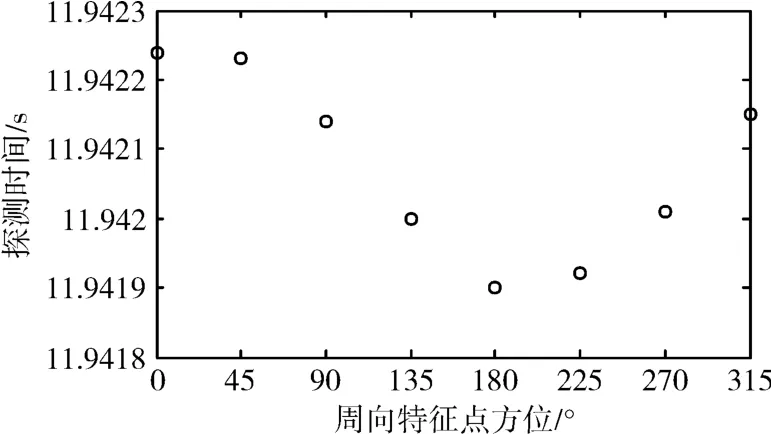
图4 引信对目标头部截面周向特征点探测时间

引信实际探测时间、距离、方位的计算结果如图5～图7所示。图中横坐标表示机体xb坐标，“o”标识数据表示各个截面实际周向探测点探测参数，实线表示三次样条插值处理后的实际探测参数。

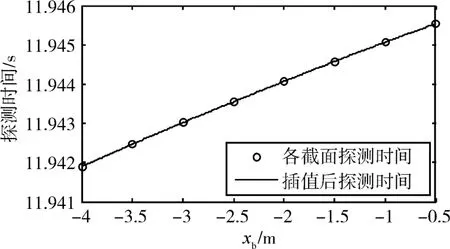
图5 引信实际探测时间结果曲线

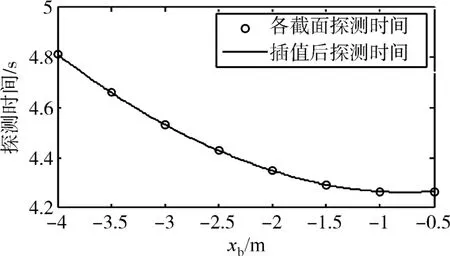
图6 引信实际探测距离结果曲线

由图5～图7可知，引信对目标从头部到尾部的探测时间逐渐增加，探测距离逐渐减小，但探测方位不变，这与图2所示的迎攻拦截条件下的弹目交会姿态一致。

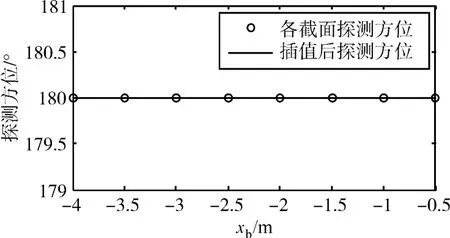
图7 引信实际探测方位结果曲线

4 结语

本文研究了基于Matlab的引信探测参数计算程序实现方法。该方法中的建立目标多截面特征点矩阵模型、拟合处理弹目运动测量数据、插值处理多截面探测参数等算法，充分利用了Matlab软件矩阵计算简便、数学函数丰富的优势。程序代码简练、使用维护简单。研究及实例运行表明，探测参数计算方法及程序正确，结果直观详细，适用于引信对导弹类目标探测参数的计算。