基于最小二乘法椭圆拟合的改进型快速算法*
朱森荣 刘杰徽
(1.海军工程大学兵器工程学院 武汉 430033)(2.重庆前卫科技集团有限公司技术中心 重庆 401121)
1 引言
椭圆拟合在图像识别、特征提取中有着特别重要的意义。而最小二乘法是数据拟合的最常用方法,受随机噪声的影响整体最小[1],是电子罗盘校准算法中应用最常用的算法之一,广泛应用于航空、航天、航海、水中兵器、石油钻井等领域[2]。
在实际应用过程中往往通过大量的数据进行拟合,计算量偏大,而单片机的算力每秒只有几万次浮点运算能力,而椭圆拟合需要快速而且大量的浮点运算资源,如果需要在单片机上进行曲线拟合的话就会大大影响系统的性能,因而需要进一步研究快速算法,在计算资源严重缺乏的单片机上算法的简化显得尤为重要[3]。
本文给予最小二乘法进行了一些简单的改进,引入样本点分组原理,再对样本点进行随机抽取,并且通过Matlab仿真验证可以一定程度上减少算法的复杂度,提升算法的实时性。
2 最小二乘椭圆拟合方法介绍
椭圆的代数表达式如下:
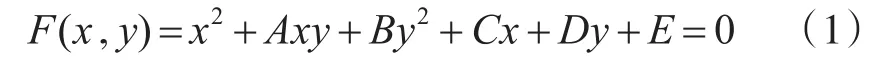
表达式中有5个未知数,分别为A、B、C、D、E。
最小二乘法是由最大似然法推出的一个最优估计技术,它可使测量误差的平方和最小,也就是所有离散点到曲线的代数误差之和最小[4],因此也被视为从一组测量值中求出一组未知量的最可信赖的方法之一[5]。
平面内某点(x0,y0)到方程(fx,y)=0所代表曲线的代数距离就是f(x0,y0),对离散样本点进行最小二乘处理,即目标函数如下
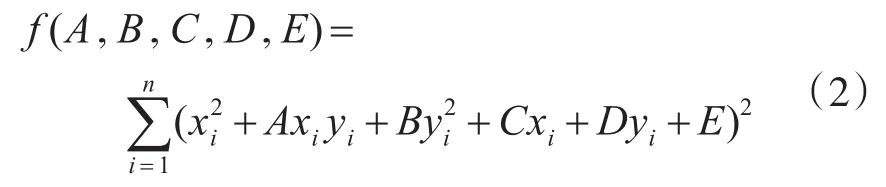
根据椭圆的几何知识,可以计算出椭圆的五个参数:位置参数(θ,x0,y0)和形状参数(a,b)。
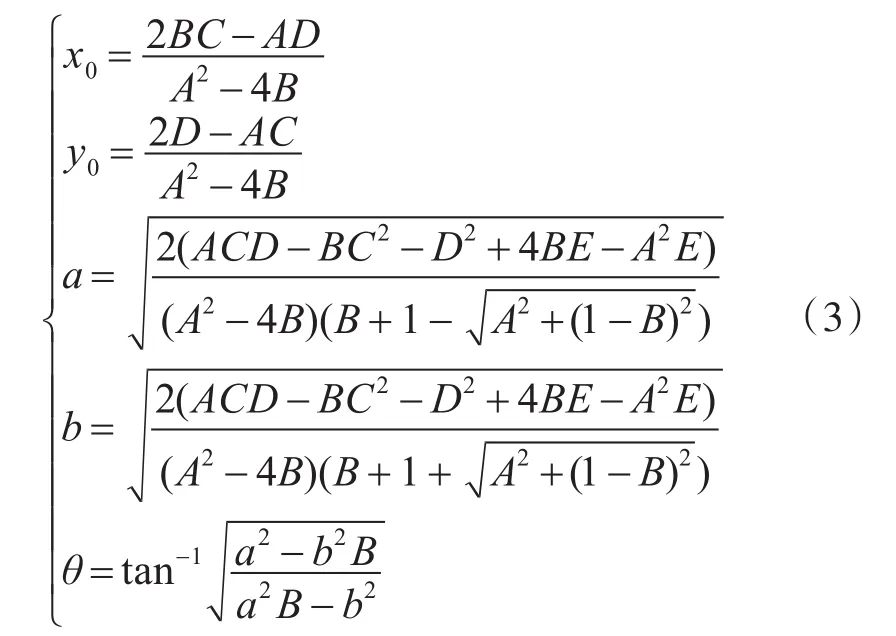
算法步骤如下[6]:
1)在总的样本空间随机选取N个样本点;
2)利用最小二乘法求解椭圆参数A、B、C、D、E;
3)计算所有样本点的匹配度;
4)重复步骤1)~3)一定次数(根据样本点个数、匹配精度和运行时间等综合因素进行调整),选取最高匹配度的拟合参数。
3 改进型椭圆拟合方法
根据数据样本每个点在椭圆上位置的不同对椭圆拟合参数估计的贡献是不同的[7],导致样本点的选取对椭圆的拟合会产生一定的偏差,尤其是样本点相对集中会使拟合结果的曲率和方向都明显变化,使得匹配度大大下降,样本点的选取成为了关键。
本方法在进行最小二乘法拟合之前在空间上对样本进行若干个区域的均匀划分(区域个数与单次拟合的样本点的个数相同)。本文改进的最小二乘法也是在随机N样本点椭圆拟合的基础上进行改进,其计算步骤如下。
1)根据曲线拟合所需的点数进行样本点分区,均匀分成N个区域,如图1所示。
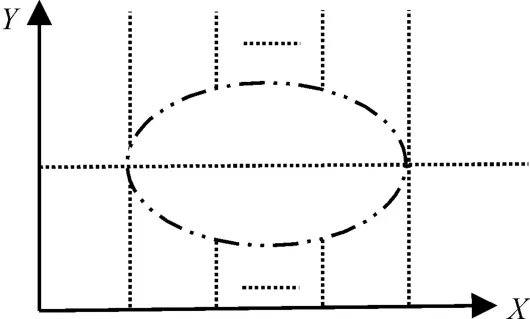
图1 样本点分区
2)每个区域进行随机选取样本点,得到N个样本点。
3)采用最小二乘法求解A、B、C、D、E个参数。
4)根据求解的椭圆参数求出椭圆的焦点坐标F0(x0,y0),F1(x1,y1)和椭圆上的点到焦点F0,F1的距离之和L。
5)根据椭圆的定义,求解所有样本点到焦点F1,F2的距离与L差的绝对值,与自定义的阈值进行比较,大于则判定为不匹配点,小于等于则判定为匹配点,得出这组参数的一个匹配百分比[8]。
6)重复2)~5)步骤一定次数(根据样本点个数、匹配精度和运行时间等进行调整),选取匹配度最高的椭圆参数(A、B、C、D、E)。
4 仿真应用结果分析
4.1 算法对对匹配度的影响
通过Matlab重复400次的仿真分析拟合结果来看,如图2所示经过本算法的改进高匹配度出现频次明显提高,最高匹配度存在一定程度的提升,满足算法最基本的匹配度要求。
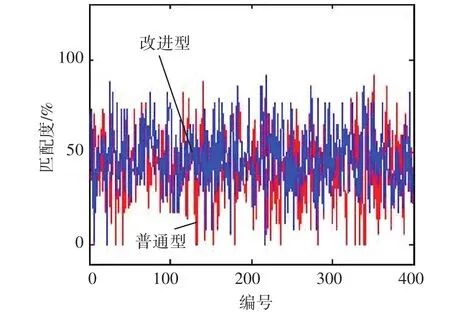
图2 匹配度
4.2 匹配度的提升分析
由于样本点是随机取样,匹配度波动很大,很难直观的给出总体的评价。而移动平均法可以消除随机波动的影响,显示出匹配度的发展趋势[9],移动平均计算公式如下:
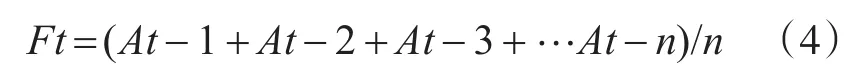
Ft为对下一个周期的匹配度;n为移动平均的周期个数;At-1为当前匹配次数的匹配度;At-2,At-3和At-n表示前两次、前三次直至前n次的匹配度值[10];
在经过20为周期的移动平均法计算[11],如图3所示,改进型最小二乘法拟合的系数匹配度整体上看明显高于普通型。
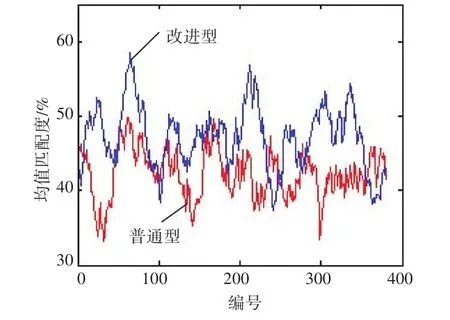
图3 均值匹配度
从本次仿真的结果来看,改进型最小二乘法在样本点选取阶段就可以一定程度排除匹配度较小的样本点组合。在样本点个数、匹配精度等条件相同的情况下,可以用较小的的拟合次数达到普通型的效果。
5 结语
普通型最小二乘法在样本点选取时是随机的,当随机的样本点相对集中时,拟合的误差就会相对较大,出现低匹配度的概率就会增加,浪费了算力资源。改进的最小二乘法恰好规避了这部分样本点组合,增加了高匹配度拟合结果出现的概率,可以适当减少重复拟合的次数,节省了算力资源,特别是在一些图像识别领域兼顾了实时性和准确性之间的矛盾[12]。

