一类带粘性项的抛物方程解的存在性和爆破性

杜玉阁,田书英

(武汉理工大学理学院,湖北 武汉 430070)

1 引言

本文研究以下具有多项式非线性项和粘性项的非线性抛物方程的初边值问题

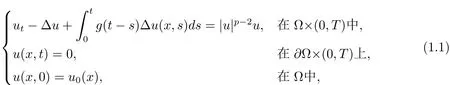
材料学和力学中对粘弹性的应用非常广泛,其中粘弹性依赖于温度和外力作用的时间.所谓的粘弹性是指任何物体对其本身的形变历史都具有一个长期的记忆[1].特别的,当研究具有记忆材料的热传导时,经典的Fourier定律被以下形式所取代

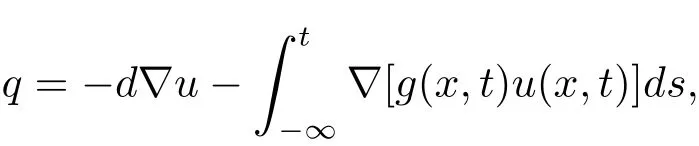
其中q与单位长度的温差成正比,u是温度,d是热传导系数,积分项表示材料中的记忆效应,q不是线性地依赖于u.对于这类问题的研究引起了广泛的关注,本文将研究该类问题(1.1)的解的存在性和爆破性.当方程(1.1)中的g=0时,方程如下

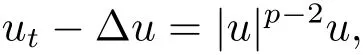
可以描述诸多化学反应、热传导过程和种群动力学.针对这类问题在解的存在性方面可以参考文献[2–5].关于解的爆破性方面也得到了广泛的研究,可参考文献[6–12].

当方程(1.1)中的g/=0时,可以描述电流变流体的扩散和记忆材料中的热传导(见文献[13,14]).由于粘弹性项的影响,问题变得更加复杂,为了解决相关问题,需要对g进行精确的估计和细致的观察.近年来,也有不少相关的研究.在g和p满足合适的条件下,Messaoudi[15,16]给出了方程的强解在有限时刻内爆破的证明.之后,Tian[17]在此基础上建立了一个新的爆破准则,利用微分不等式技巧给出了解的爆破时间的上界.Di等[18]和Sun等[19]研究了含有Δut项的非线性拟抛物方程解的存在性和爆破性问题.还有一些相关的研究,可以参考文献[20–22].本文假设以下条件

条件Ag:→是有界的C1函数,满足

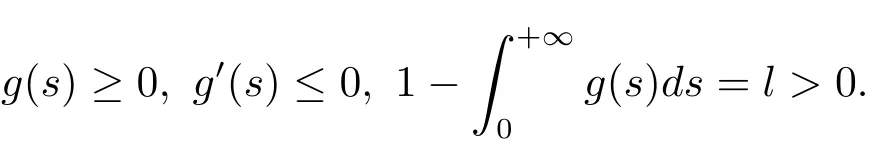
条件B常数p满足

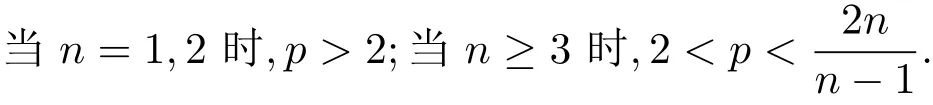
定义1.1(弱解)对任意v∈(Ω),t∈(0,T),函数u(x,t)满足u(x,t)∈L∞(0,+∞;(Ω)),ut(x,t)∈L2(0,+∞;(Ω))及以下方程

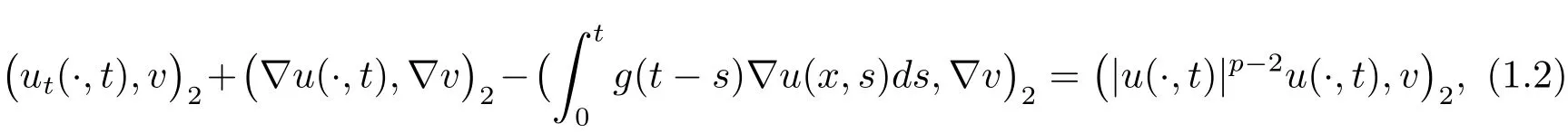
则称 u=u(x,t)是方程 (1.1)的弱解,其中 u(x,0)=u0(x)∈(Ω),(·,·)2表示内积

定义1.2(最大存在时间)设u(x,t)为方程(1.1)的弱解.我们定义u(x,t)的最大存在时间T如下:

(1)若对任意0≤t＜+∞,u(x,t)都存在,则T=+∞.

(2)若存在t0∈(0,+∞)使得当0≤t＜t0时,u(x,t)存在,但在t=t0处u(x,t)不存在,

则T=t0.

定义1.3(有限时刻爆破)设u(x,t)为方程(1.1)的弱解.如果u(x,t)的最大存在时间T是有限的,且满足

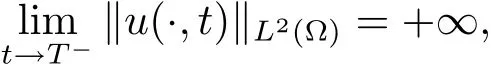
则称u(x,t)在有限时刻爆破.

为了说明本文的主要结果,需要引入以下修正的能量泛函

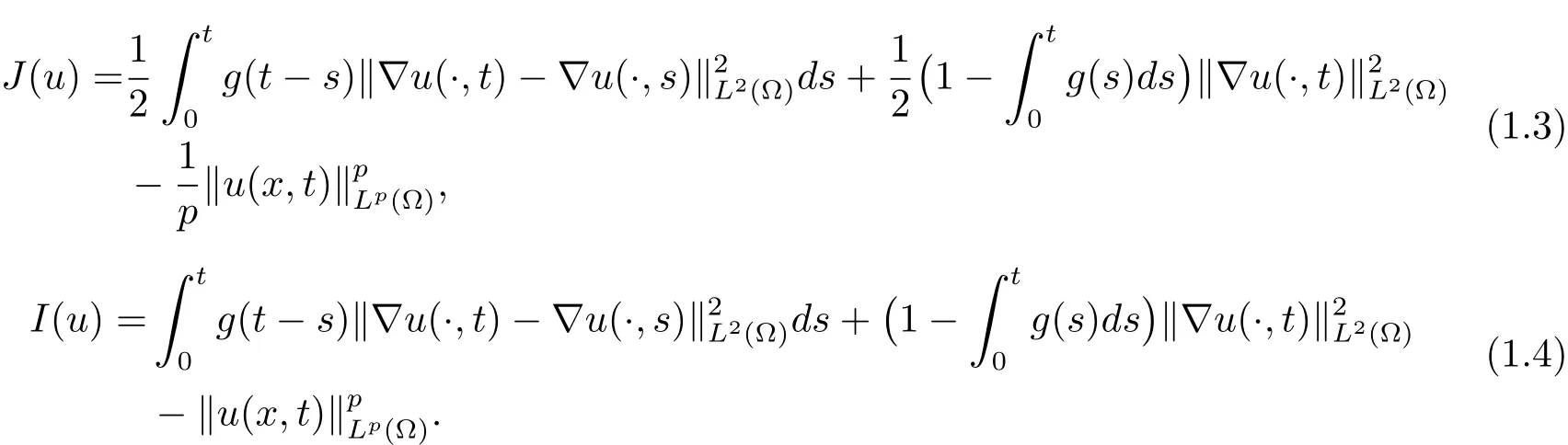
则有

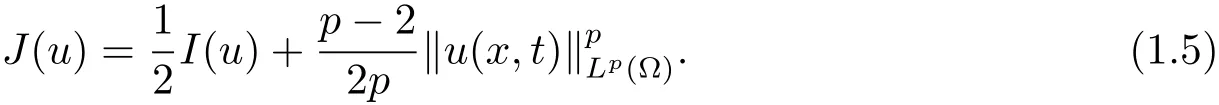
本文的主要结果如下.

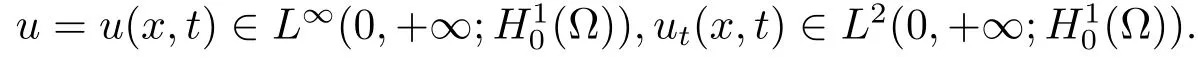
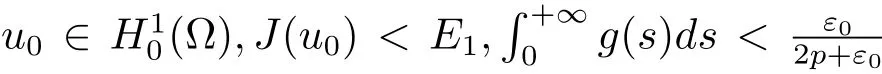
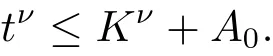
这里E1＞0见(3.3)式,0＜ε0＜p-2,常数K 满足 supp(u0)⊂BK(0),常数0＜ν＜1,A0＞0见(3.14)式.

注1.1在g和p具有相似但不同的限制条件下,Messaoudi[15,16]证明了具有正、负或消失的初始能量时(初始能量都满足J(u0)＜E0,E0＞0)该方程的解在有限时刻爆破.在定理1.2中,我们将这一能量范围进行了扩大,得到一个新的更大的能量范围E1,即E0＜E1,具体证明见(3.5)式.

注1.2在定理1.2的条件下,可以得出I(u0)＜0,与定理1.1不存在冲突.

本文结构如下:在第2节中,利用位势井理论和Galerkin方法给出定理1.1的证明.在第3节中,给出相关引理和定理1.2的证明.

2 解的存在性

为了证明方程解的存在性,需要定义

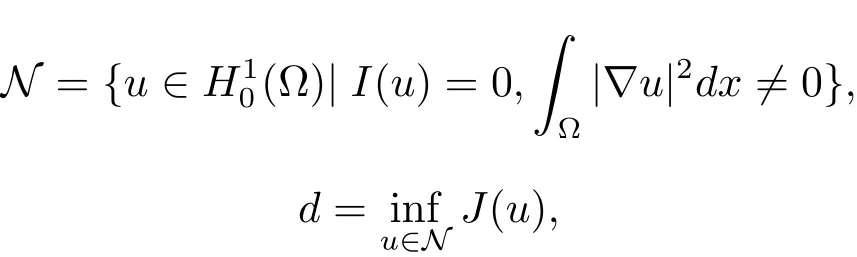
显然有d＞0.从而,定义

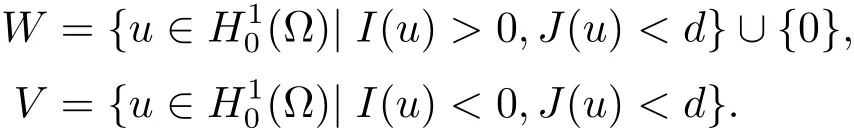
接下来给出能量恒等式.

引理2.1

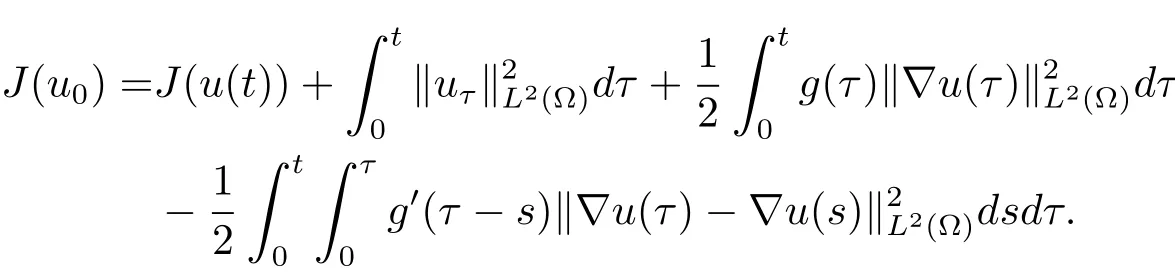
这里J(u(t))=J(u),见(1.3)式.事实上,由于u=u(x,t)是x,t的函数,由(1.3)式可知,J(u)是t的函数,为了突出这一点,故用记号J(u(t)).后文会用到类似的其他记号.

证明结合(1.3)式,定义

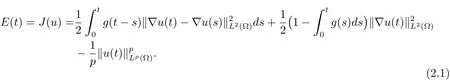
利用(1.2)式,可得

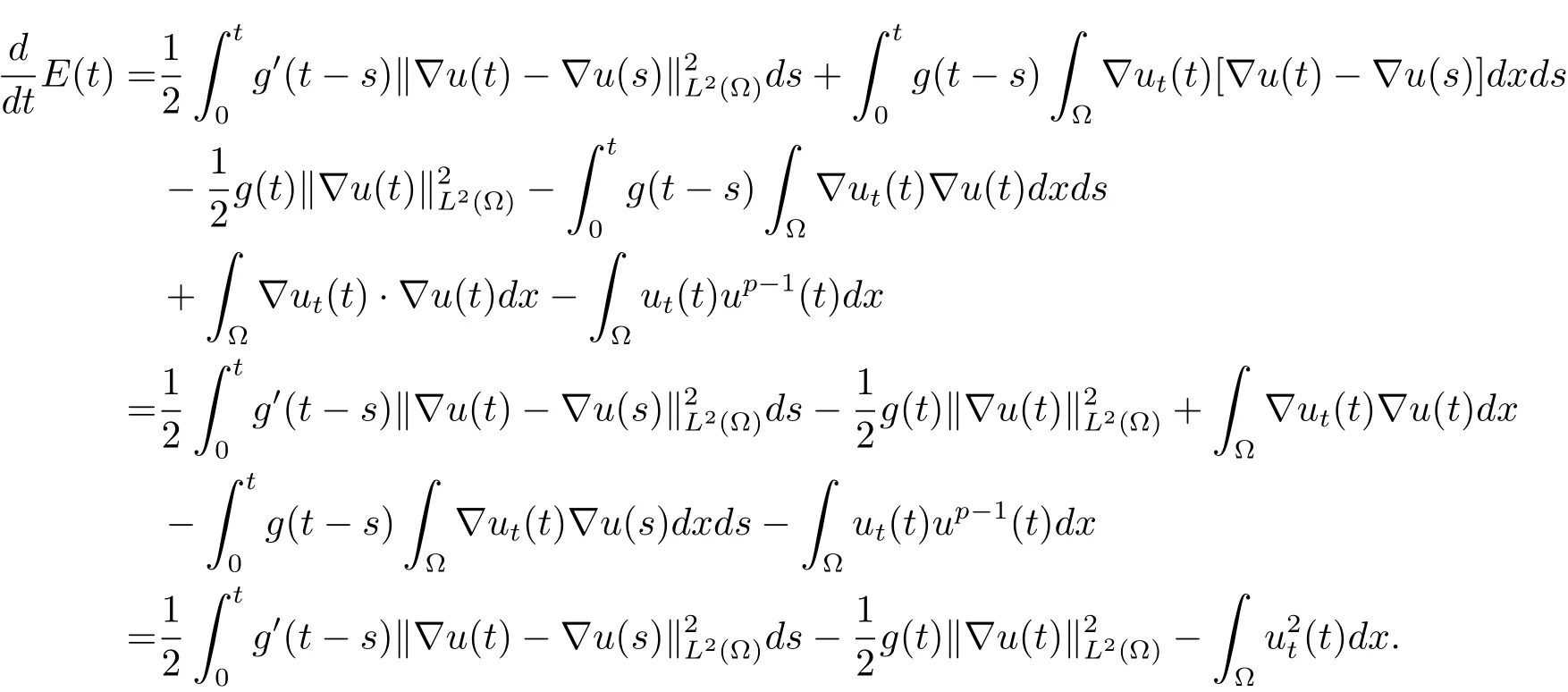
上式两端在[0,t]上进行积分,可得

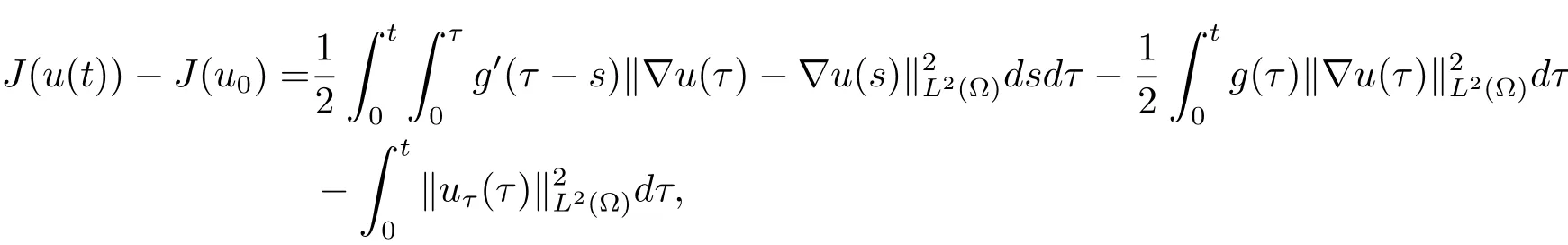
从而引理2.1得证.

现在,给出方程解的存在性的证明.

证明定理1.1在J(u0)＜d,I(u0)≥0时,不难得到J(u0)≥0.考虑若J(u0)=0且I(u0)≥0,则u0=0,这是一个平凡解.若J(u0)＞0,I(u0)=0,则有RΩ|∇u0|2dx/=0,进而J(u0)≥d,这与J(u0)＜d相矛盾.所以我们只需考虑0＜J(u0)＜d,I(u0)＞0的情况.

下面利用Galerkin方法构造问题(1.1)的近似解um(x,t).我们选择{ωj(x)}作为(Ω)上的一组正交基,令

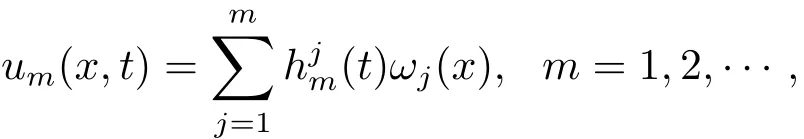
且对于 k=1,2,···,m,满足

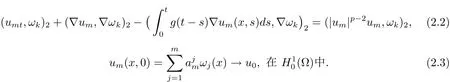
同时,当m足够大,且t∈[0,T)时(T是um(x,t)的最大存在时间),能量恒等式如下

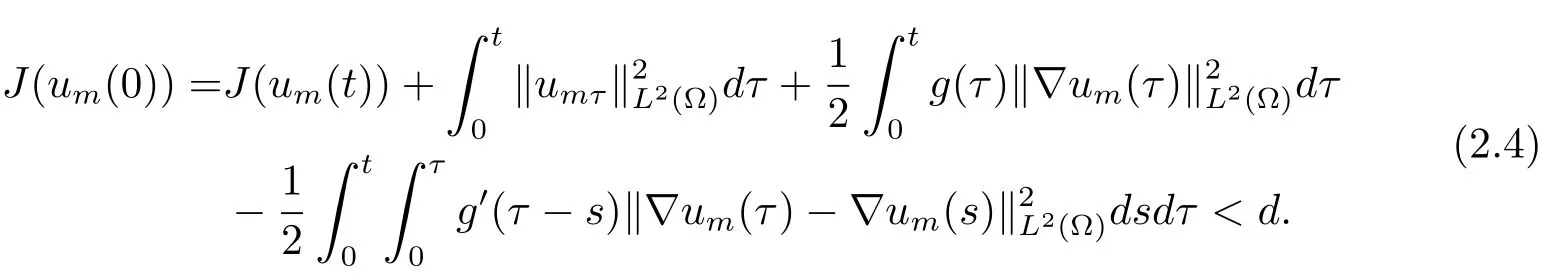
现在证明对于足够大的m和任意的0≤t＜T,有um(x,t)∈W.假设该命题不成立,则存在t0∈(0,T)使得um(x,t0)∈∂W,从而

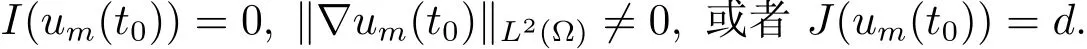
结合 (2.4)式,可知 J(um(t0))=d不成立.又若 I(um(t0))=0,‖∇um(t0)‖L2(Ω)/=0,根据d的定义,有J(um(t0))≥d,这与(2.4)式相矛盾.从而可得,对足够大的m 和任意的0≤t＜T,有um(x,t)∈W.进而,以um(x,T)为初始能量,重复上述讨论,则对于足够大的m和任意的0≤t＜+∞,都有um(x,t)∈W.

根据

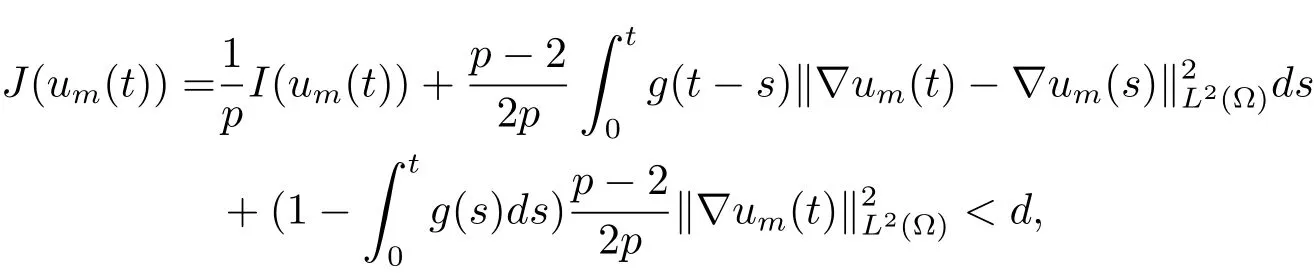
可知

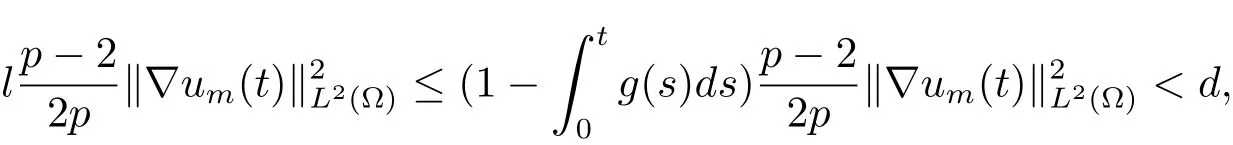
则有

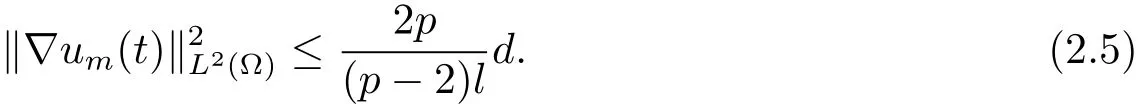
由(2.4)式可以得到

另一方面,通过计算可得如下结果

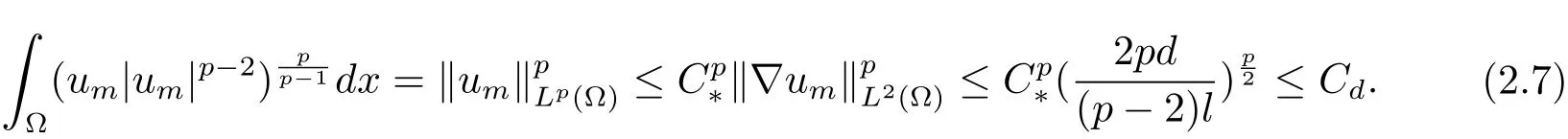
这里C*是Sobolev空间(Ω)→Lp(Ω)的最佳嵌入常数.

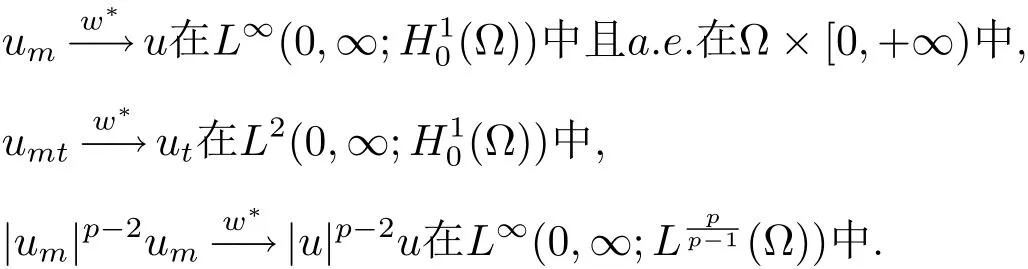
因此,在(2.2)式中,当k固定,m-→+∞ 时,有

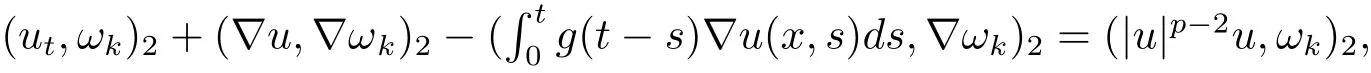
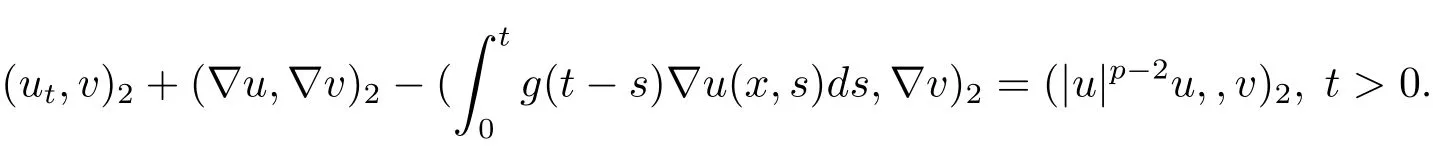
同时,从(2.3)式中,可以得到u(x,0)=u0(x)∈(Ω).因此,u是问题(1.1)的全局弱解.定理1.1证毕.

3 解在有限时刻爆破

在证明解的爆破性之前,先介绍一个必需的引理.已知能量函数(见(2.1)式)

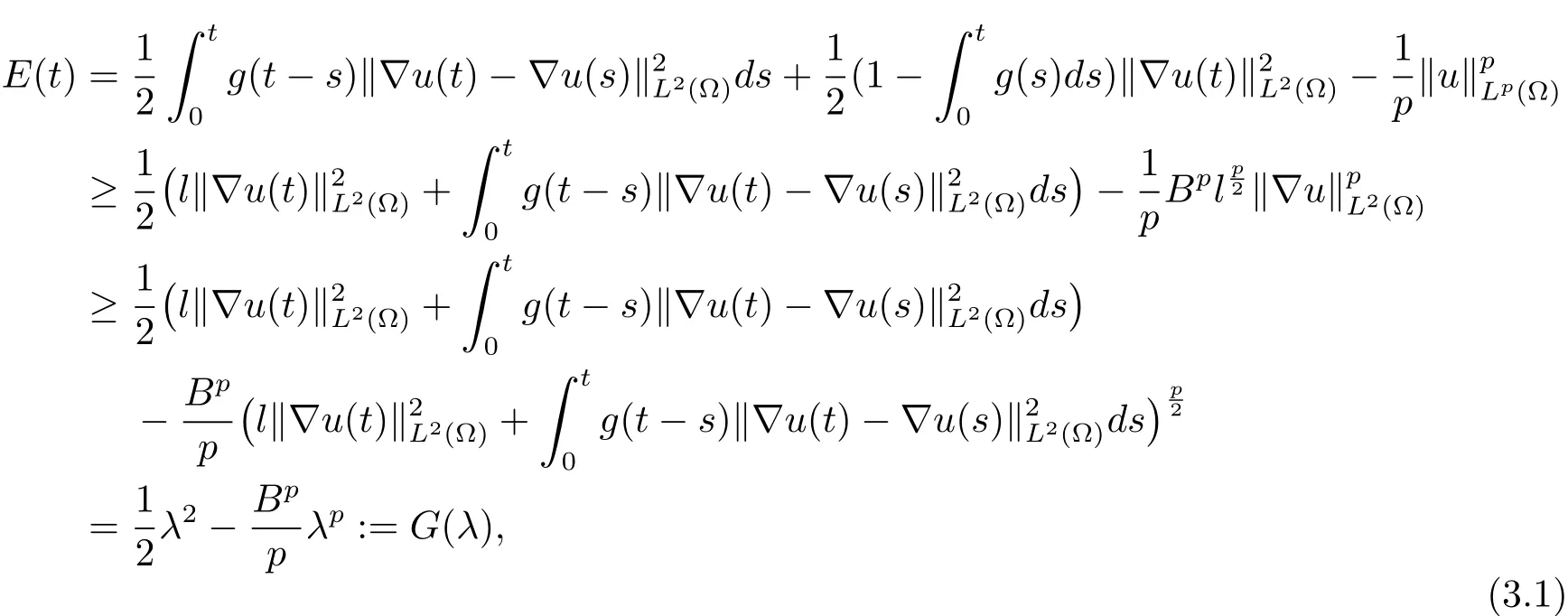
这里B=C*/l(C*是Sobolev空间(Ω)→Lp(Ω)的最佳嵌入常数),

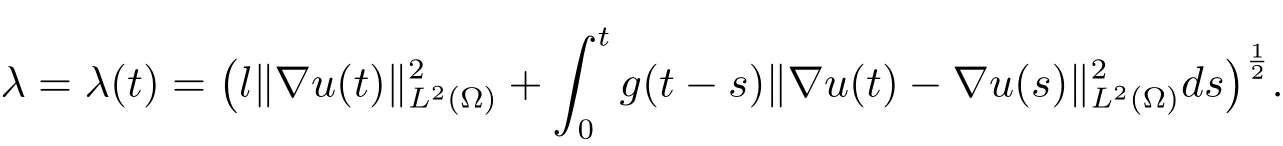
则有

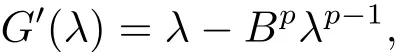
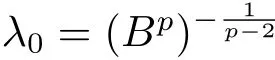
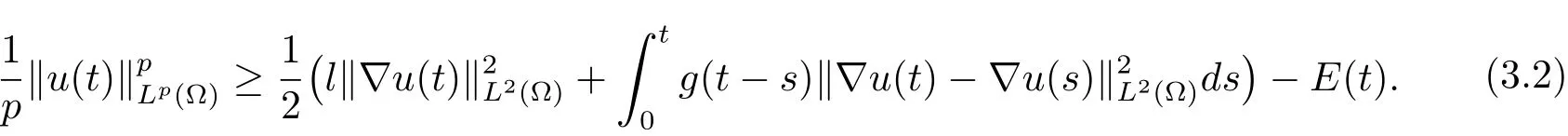
设u(x,t)是问题(1.1)的弱解,令

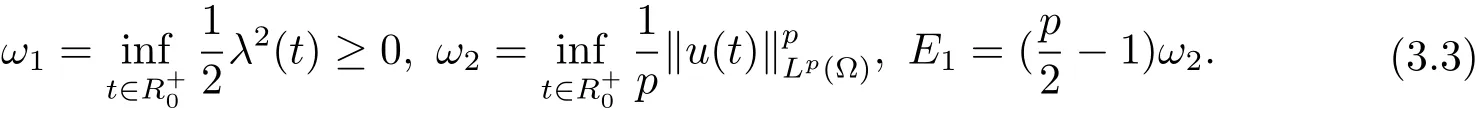
引理3.1设u(x,t)是方程(1.1)的弱解.若J(u0)＜E1,则对任意的t∈[0,T),都有ω2＞ 0,λ(t)＞ λ0,E(t)＜ E1,E0＜ E1.

证明由引理2.1和(3.2)式可知,对∀t∈[0,T)

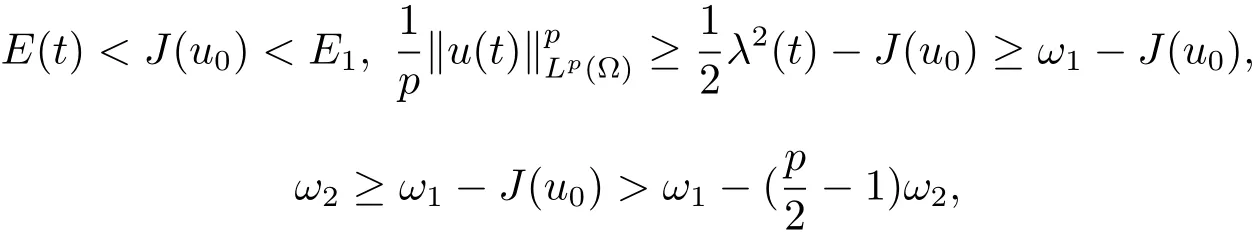
于是有

由Sobolev嵌入定理,可得

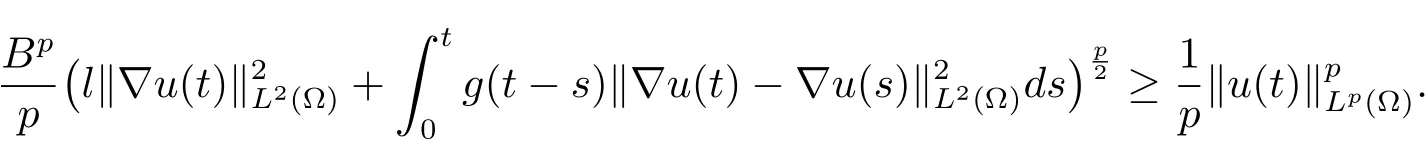
则有

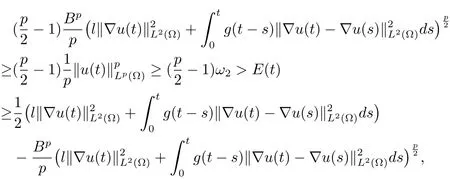
因此,可以得到

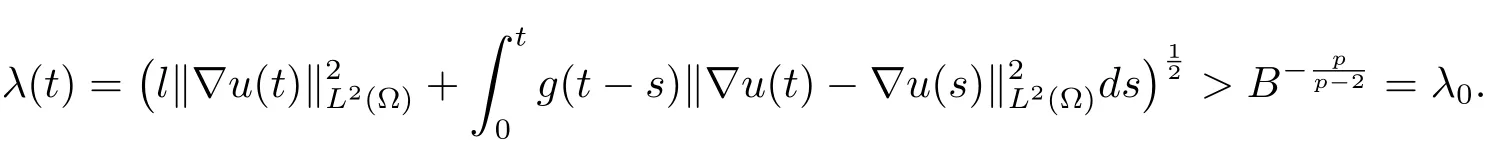
再结合(3.3)式,可以得到

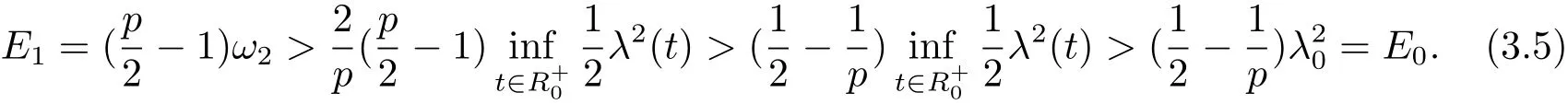
引理3.1得证.

接下来给出方程解的爆破性的证明及爆破时间的上界.

证明定理1.2由J(u0)＜E1,定义H(t)=E2-E(t),其中 E2∈([J(u0)]+,E1)且E2＞0,则有

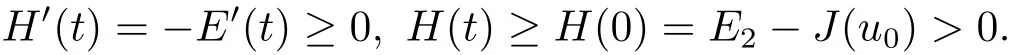
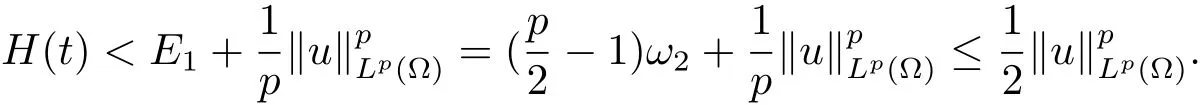
所以

结合ω2＞0,0＜E2＜E1,取足够小的ε0＞0,使得

这意味着ε0＜p-2.接下来,定义加权函数

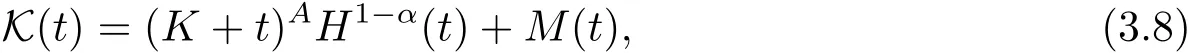
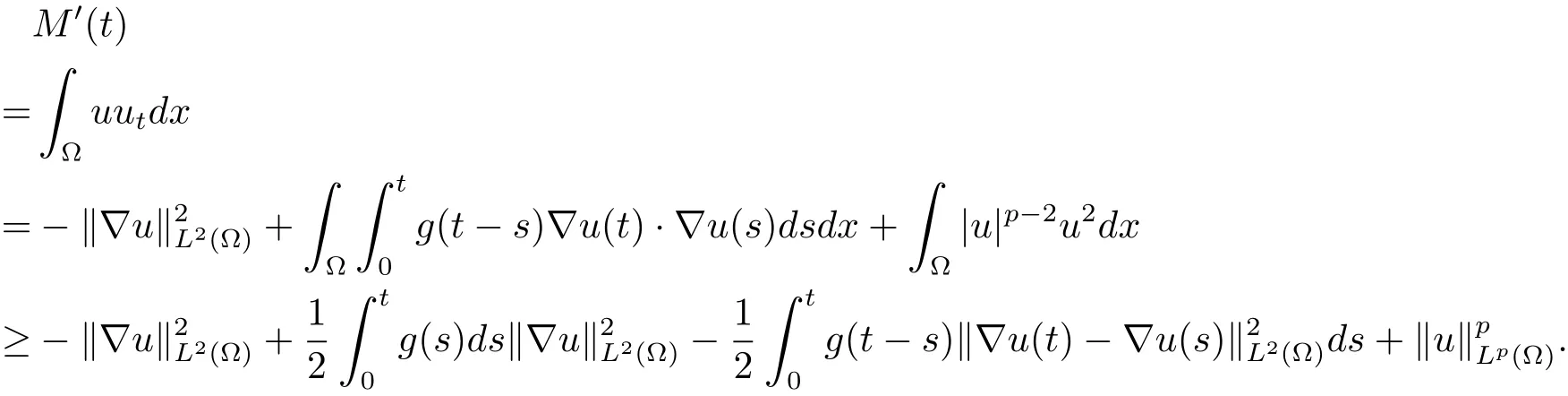
利用(3.1)式和(3.7)式,不等式右边加上一项-(p-ε0)E(t)+(p-ε0)E(t),可得

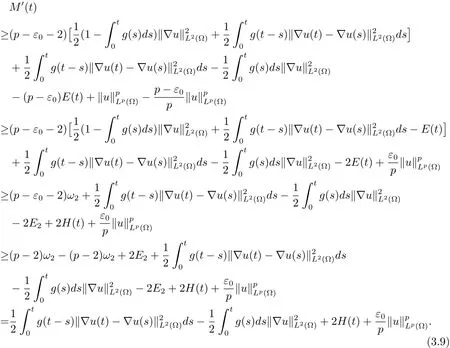
通过(3.8)式和(3.9)式,可以得到

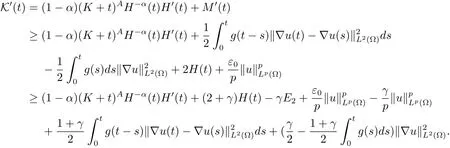
这里γ＞0.根据ω2和E1的定义,则(3.6)式变形为如下形式

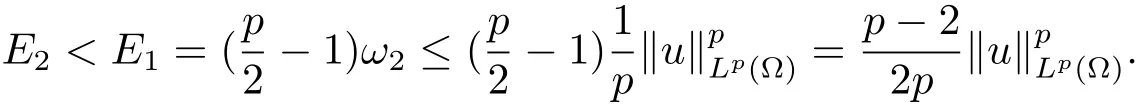
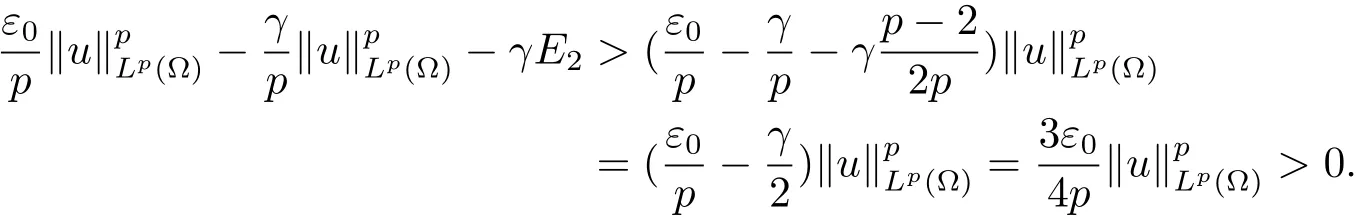
因此

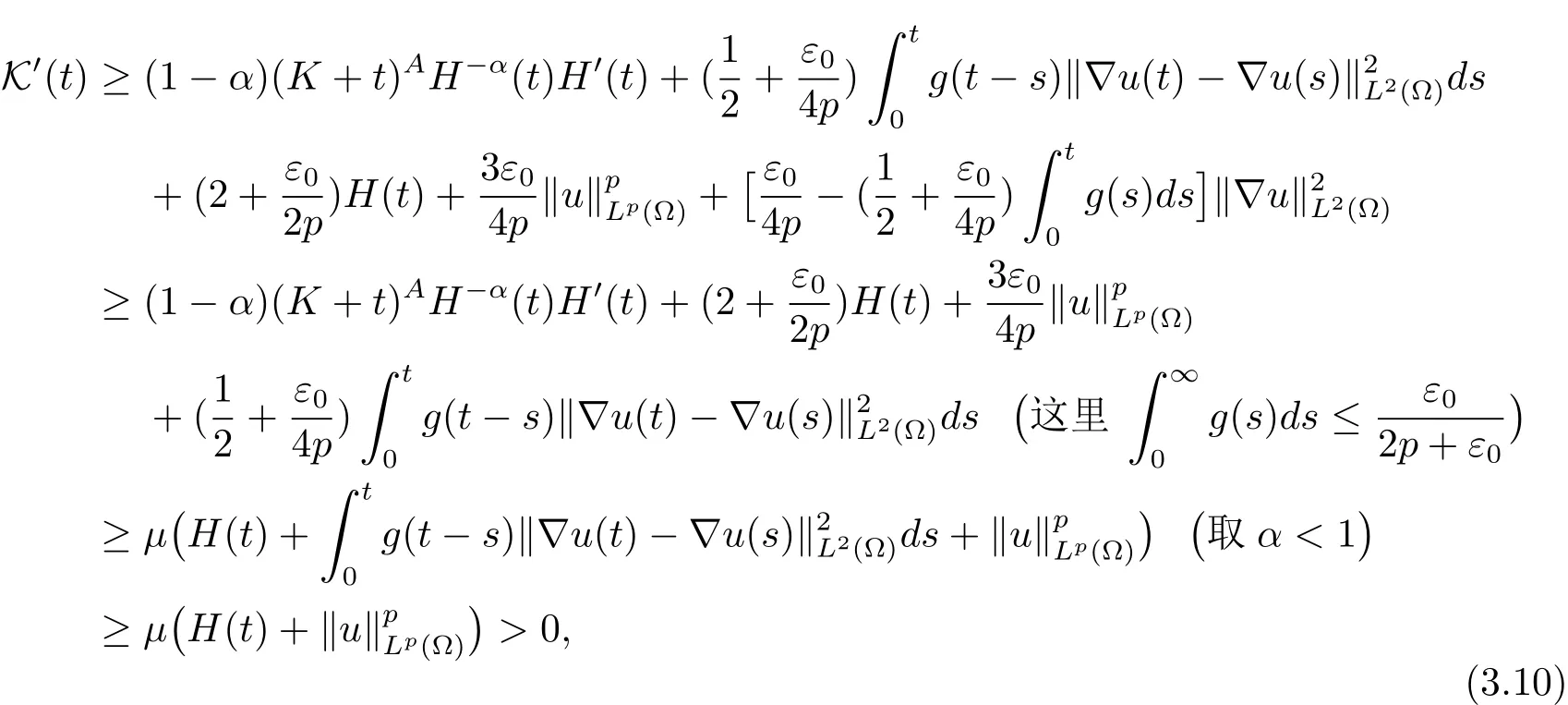
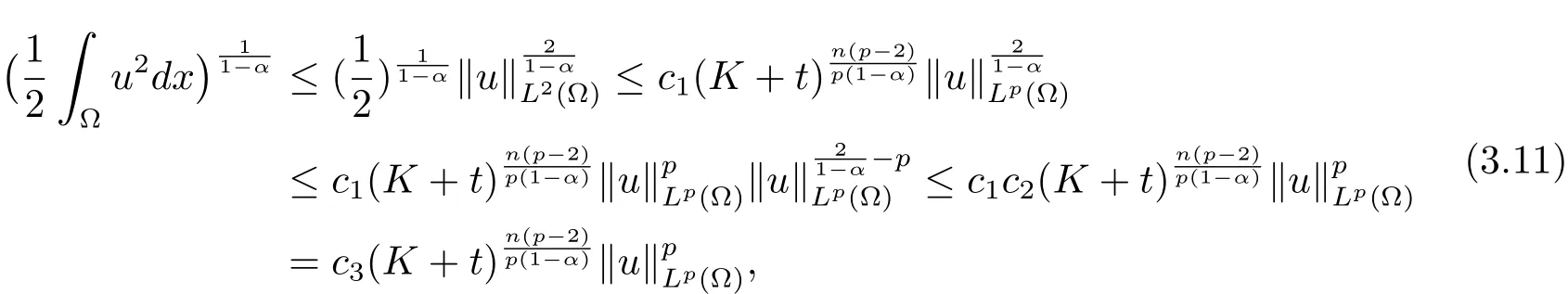
再根据(3.8)和(3.11)式,有

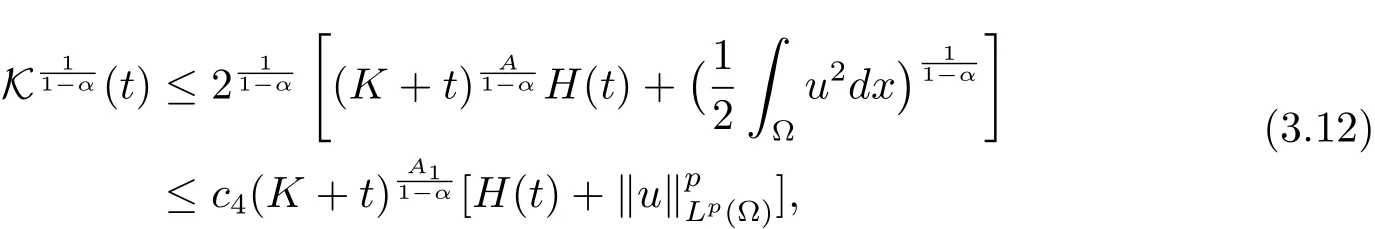
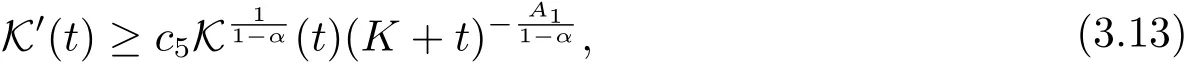
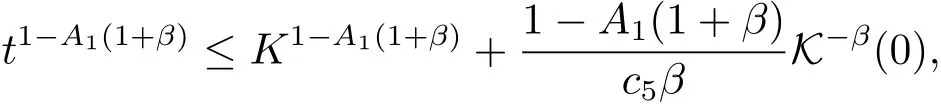
即tν≤ Kν+A0,其中

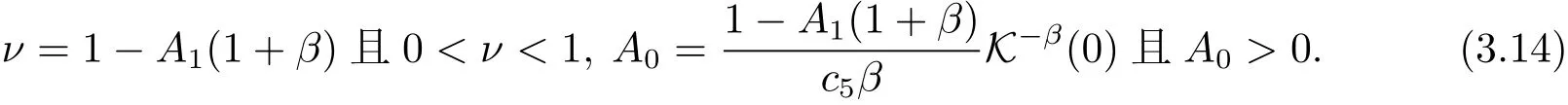
定理1.2证毕.