TOPSIS法和秩和比法模糊联合在基本公共卫生服务质量综合评价中的应用研究

顾思雨，梁园园，章凯燕，杨金侠

方法学介绍：

逼近理想解排序法（TOPSIS）由HWANG C L和YOON K于1981年提出，其基本原理是通过同趋势化处理和归一化矩阵，找出多个目标中的最优目标和最劣目标，计算其欧氏距离，获得各指标值与理想解的接近程度并进行排序，以此作为评价目标优劣的依据。秩和比法由田凤调教授于1988年提出，其基本原理是在一个n×m矩阵中，通过对指标进行编秩，从而获得无量纲的统计量——RSR，并依据RSR值对评价对象按优劣排序。

TOPSIS法和秩和比法都是多目标决策分析中常用的评价方法，目前广泛应用于卫生评价、卫生决策等领域。但是，TOPSIS法利用指标的全距间接进行评价，易受离散程度较大值的影响，而秩和比法在非参数转化中将指标用秩来代换，易造成信息损失现象。将TOPSIS法和秩和比法模糊联合，一方面能够弥补单一使用TOPSIS法或秩和比法的不足，另一方面能够充分利用模糊联合的特点与优势，从比值权重、分档计算的方法角度进行综合分析，提高评价结果的准确性。

国家基本公共卫生服务项目是国家根据居民的健康情况和健康需求，向全体居民提供的共同性服务项目和向重点人群提供的针对性服务项目，旨在促进健康公平和实现全民健康。基本公共卫生服务项目的实施有助于落实以基层为重点、预防为主的工作方针，促进基本公共卫生服务均等化［1］。国家基本公共卫生服务项目于2009年启动，如今已实施十年有余，并逐渐成为基层医疗卫生机构的工作重心，服务质量备受关注。对基本公共卫生服务质量进行综合评价，以评价方法为手段，以评价结果为依据，能为调整相关政策和提高服务质量提供依据。目前，综合评价基本公共卫生服务质量的常用方法有逼近理想解排序法（TOPSIS法）、秩和比法、数据包络法（DEA），但各有其局限性，将一些方法适当联合应用能够有效弥补不足。本研究从基本公共卫生服务项目运行和实施的角度，收集Z省24家基层医疗卫生机构2018年基本公共卫生服务项目的实施数据，运用 TOPSIS法［2］、秩和比法［3］及二者模糊联合法［4］对Z省基本公共卫生服务质量进行综合评价，旨在探索适宜的基本公共卫生服务质量综合评价方法，为调整相关政策和提高服务质量提供依据。

1 对象与方法

1.1 研究对象 由于Z省各地级市差异较大，经过专家会议商议决定，依据社会经济发展状况，采用多阶段立意抽样法确定调查对象，缩小抽样单元之间的差异以保证样本代表性，并于2019年2—4月展开调研。第一阶段，在Z省南部、中部和北部地区各抽取2个地级市，共抽取6个地级市；第二阶段，在抽取的6个地市级中，随机选取1个区和1个县，共选取12个市辖区（县）；第三阶段，在抽取的12个市辖区（县）中，随机抽取2家社区卫生服务中心（乡镇卫生院），共选取24家社区卫生服务中心（乡镇卫生院）为评价对象（记为机构A～X）。

1.2 研究方法

1.2.1 数据收集方法 经Z省卫生健康委员会下发通知，由24家基层医疗卫生机构基本公共卫生相关负责人填写《基层医疗卫生机构基本公共卫生服务项目开展情况表》，收集2018年24家基层医疗卫生机构基本公共卫生服务实施数据。“2018年国家基本公共卫生服务项目”［5］确定了14项评价指标，由于每家样本机构的传染病疫情报告率与卫生监督协管信息报告率均为100%，因此本研究未将这两项指标纳入评价，选取其余12项指标作为评价指标，分别为：健康档案建档率（X1）、新生儿访视率（X2）、儿童健康管理率（X3）、早孕建册率（X4）、产后访视率（X5）、老年人健康管理率（X6）、高血压患者规范管理率（X7）、2型糖尿病患者规范管理率（X8）、结核病患者规范管理率（X9）、严重精神障碍患者规范管理率（X10）、老年人中医药健康管理率（X11）、儿童中医药健康管理率（X12）。采用Excel 2010软件对数据进行录入和运算。

1.2.2 数据分析方法

1.2.2.1 TOPSIS法 TOPSIS法主要面向多目标决策，通过同趋势化处理和归一化矩阵，找出多个目标中的最优目标和最劣目标，计算其欧氏距离，获得各指标值与理想解的接近程度并进行排序，以此作为评价目标优劣的依据［2］。

1.2.2.2 秩和比法 秩和比法是数量方法中常见的一种方法，在一个n×m矩阵中，通过对指标进行编秩，从而获得无量纲的统计量RSR，依据RSR值对评价对象的优劣进行排序［3］。

1.2.2.3 TOPSIS法与秩和比法模糊联合 在TOPSIS法与秩和比法单独评价的基础上结合模糊集理论［4］进行综合评价，以验证两种方法的科学性、客观性和合理性。

2 结果

2.1 24家机构12项指标开展情况 24家机构健康档案建档率、新生儿访视率、儿童健康管理率、早孕建册率、产后访视率、老年人健康管理率、高血压患者规范管理率、2型糖尿病患者规范管理率、结核病患者规范管理率、严重精神障碍患者规范管理率、老年人中医药健康管理率、儿童中医药健康管理率分别为 74.8%～100.0%、87.7%～100.0%、87.8%～100.0%、79.9%～100.0%、87.7%～100.0%、55.0%～111.9%、39.8%～100.0%、35.6%～100.0%、54.5%～100.0%、82.1%～107.5%、29.2%～100.0%、33.3%～100.0%。

2.2 TOPSIS法评价结果

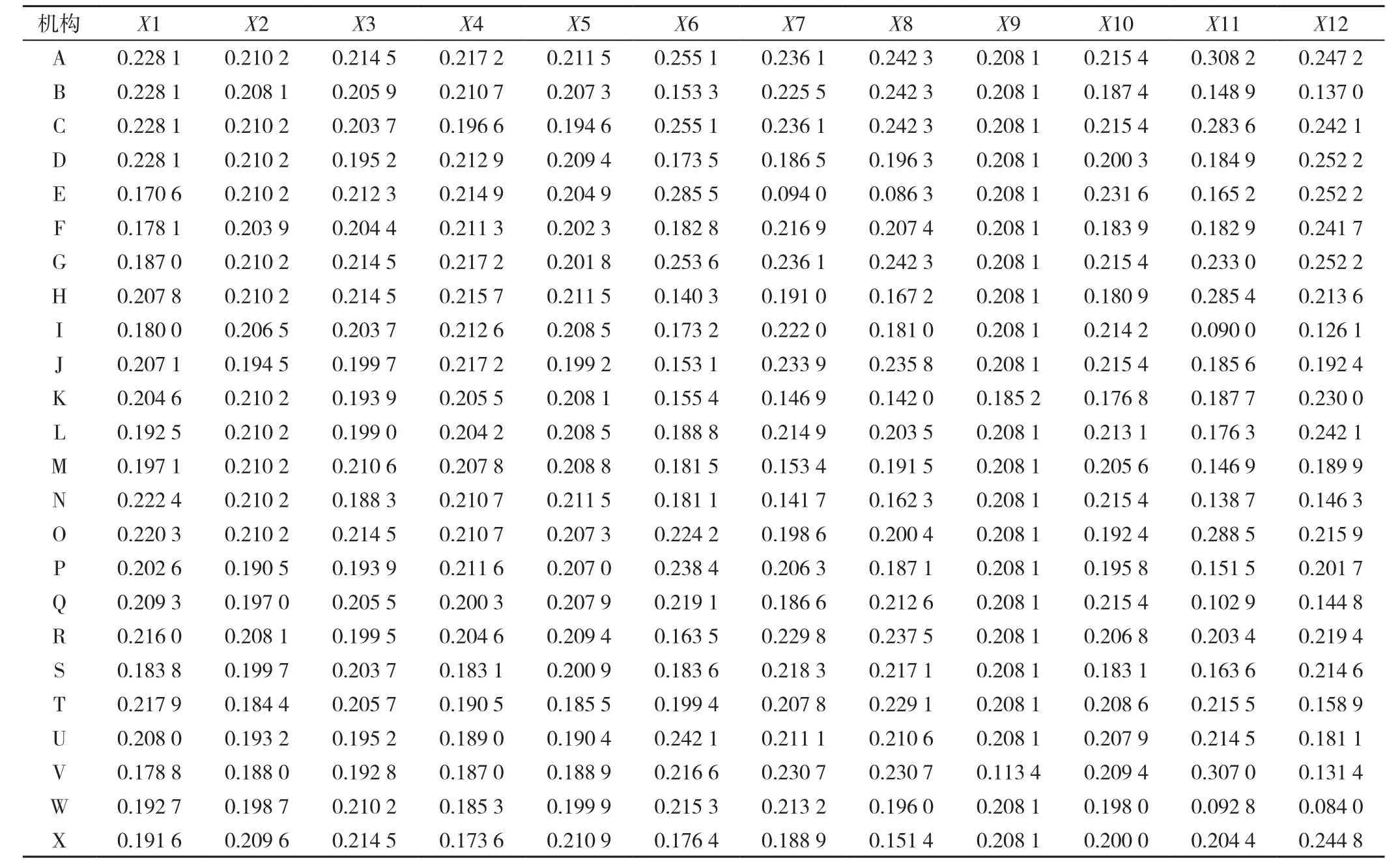
表1 基于TOPSIS法对24家社区卫生服务中心（乡镇卫生院）12项指标归一化处理后的数据Table 1 Normalized data of 24 community（township） health centers based on TOPSIS method

2.2.2 计算最优目标与最劣目标 以表1中每个评价指标的最大值作为最优目标Z+，最小值为最劣目标Z-。Z+=（0.228 1、0.210 2、0.214 5、0.217 2、0.211 5、0.285 5、0.236 1、0.242 3、0.208 1、0.231 6、0.308 2、0.252 2）；Z-=（0.170 6、0.184 4、0.188 3、0.173 6、0.185 5、0.140 3、0.094 0、0.086 3、0.113 4、0.176 8、0.090 0、0.084 0）。

结果显示：Ci的平均值为0.594 6，24个基层医疗卫生机构中A、C、D、F、G、H、L、O、R、T、U和V的Ci值均超过平均水平，B、E、I、J、K、M、N、P、Q、S、W和X的Ci值均未达到平均水平，其中Ci值排名前3名的分别为A、C和G，Ci值排名后3名的分别为N、W和I（表2）。

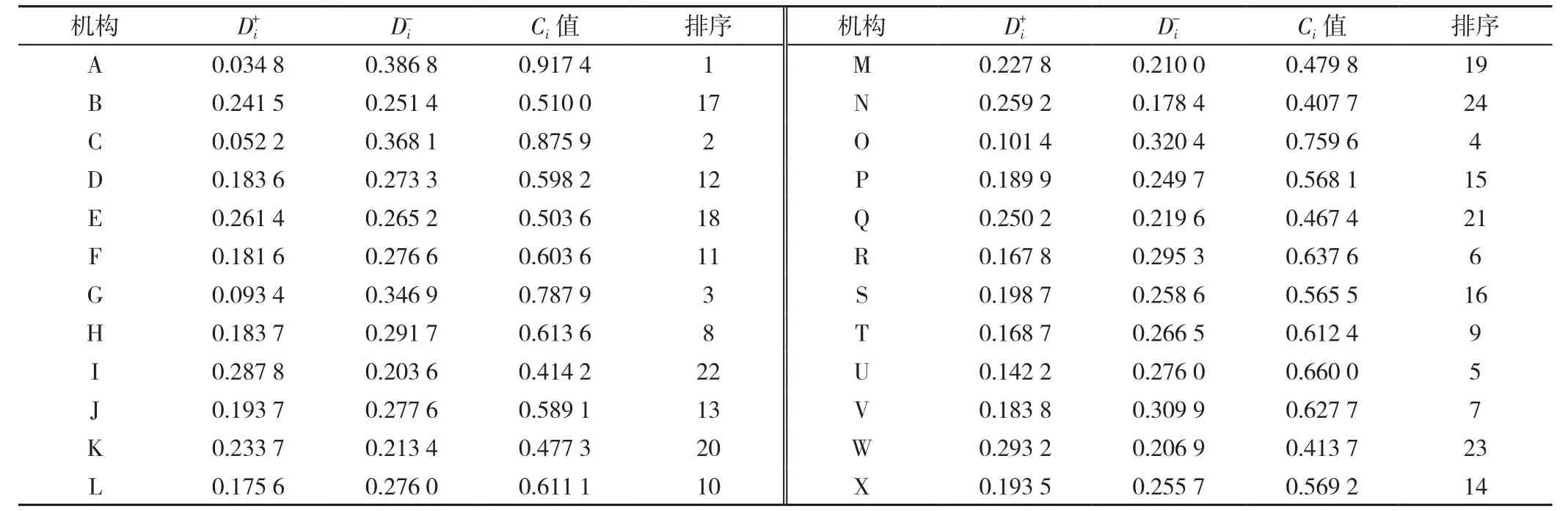
表2 24家社区卫生服务中心（乡镇卫生院）基本公共卫生服务质量综合评价Ci值及排序结果Table 2 Comprehensive evaluation of the quality of national essential public health services delivered by 24 community（township） health centers ranked by Ci value from top to bottom

2.3 秩和比法评价结果

2.3.1 对原始数据进行编秩 高优指标采取从小到大编秩，低优指标采取从大到小编秩，指标值相同的计算平均秩。本文所选12个指标均为高优指标。

2.3.2 计算RSR值 利用公式RSR=∑R/（m×n）计算各评价指标的RSR值。m=1，2，3……12；n=1，2，3……24。

2.3.3 根据RSR值进行排序 RSR值为0～1，RSR值越大越好。排序结果显示，RSR值排名前三名的分别为A、G和C，RSR值排名后三名的分别为V、W和K（表3）。

表3 24家社区卫生服务中心（乡镇卫生院）基本公共卫生服务质量综合评价的RSR值及排序结果Table 3 Ranked RSR values and RSR value-based top-to-bottom ranking of quality of national essential public health services delivered by 24 community（township） health centers

2.4 TOPSIS法和秩和比法模糊联合的评价结果 根据模糊集理论，设Ci与RSR的权重比为W1∶W2，求W1Ci∶W2RSR，并将比值分为若干档，即Ci∶RSR分别为 1∶0、0.1∶0.9、0.5∶0.5、0.9∶0.1、0∶1五档，计算各档数值并排序，依据“择多原则”［4］，排名前三名的分别为A、C和G，排名后三名的分别为I、K和W（表4）。

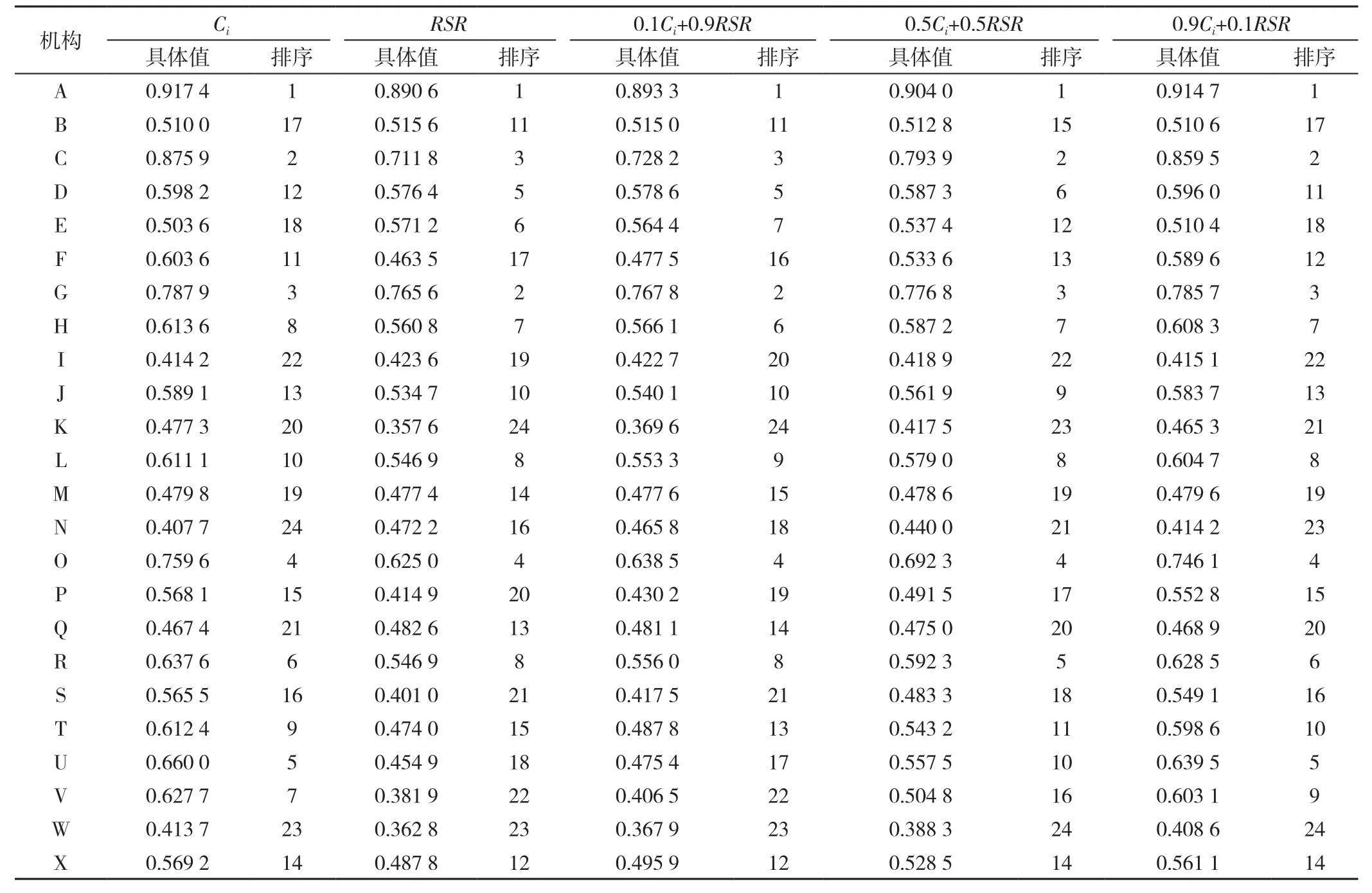
表4 基于TOPSIS法与秩和比法模糊联合的24家社区卫生服务中心（乡镇卫生院）基本公共卫生服务质量综合评价的排序结果Table 4 The top-to-bottom ranking result of the quality of national essential public health services delivered by 24 community（township） health centers assessed using fuzzy combination of TOPSIS and RSR method

3 讨论

3.1 综合评价方法分析 TOPSIS法和秩和比法是多目标决策分析中常用的两种评价方法，广泛应用于卫生评价、卫生决策等多个卫生领域［2］，但两者都存在一定局限性。TOPSIS利用指标的全距间接进行评价，易受离散程度较大值的影响，只能对每个评价对象的优劣程度进行排序，不能全面、客观地反映指标的作用，灵敏度不高；秩和比法在非参数转化中，将指标用秩来代替，易造成信息损失现象，其评价结果也存在不足［3］。将TOPSIS法、秩和比法和模糊联合法结合应用，能够弥补单独使用TOPSIS法或秩和比法的不足。另外，结合模糊集理论［4］从比值权重、分档计算的方法角度对评价对象进行综合分析，能够提高评价结果的准确性与灵敏度，对于综合评价基本公共卫生服务质量具有很高的适用性。

3.2 综合评价结果分析 基于TOPSIS法和秩和比法模糊联合的评价结果显示，Z省基层医疗卫生机构基本公共卫生服务质量存在明显差异。在TOPSIS法评价中，排名前三名的为A、C和G，排名后三名的为I、W和N；在秩和比法评价中，排名前三名的为A、G和C，排名后三名的为V、W和K；在TOPSIS法与秩和比法模糊联合的评价中，Ci档和0.9Ci∶0.1RSR档评价结果基本相同，RSR档和0.1Ci∶0.9RSR档评价结果基本相同，依据“择多原则”，排名前三名的分别为A、C和G，排名后三名的分别为I、K和W，这与TOPSIS法和秩和比法的评价结果基本一致。综上所述，Z省2018年基本公共卫生服务质量排名前三名的基层医疗卫生机构分别为A、C和G，表明A、C和G 3家基层医疗卫生机构2018年基本公共卫生服务质量较好；排名后三名的分别为I、K和W，表明I、K和W 3家基层医疗卫生机构2018年基本公共卫生服务质量相对较差。

结合实地调研情况，深入分析可知，排名较前的A、C和G机构多位于人口密集、经济发展情况较好的区域，在医疗卫生资源和服务能力方面有较好的基础，因而能提供较为优质的基本公共卫生服务；排名较后的I、K和W机构多位于人口相对稀少、经济发展状况欠佳的区域，存在基础设施薄弱、基层卫生人员和公共卫生人员稀缺、专业分工不明确等问题。徐昌娟［6］和文育锋等［7］在对该省卫生资源配置情况和基层医疗卫生机构人才状况调查时，也得到相似结论。

3.3 提高基本公共卫生服务质量的建议 本研究运用TOPSIS法、秩和比法及二者模糊联合的方法对基本公共卫生服务质量进行评价，得到的评价结果基本一致。二者模糊联合方法得到的评价结果及影响因素与实际情况一致，也和其他研究结果相一致［8-9］。针对分析得到的影响因素，提出以下建议：（1）政府部门应充分考虑不同地区的实际情况，在结构上适当向弱势地区倾斜，加大经费投入、监督管理力度，保证城乡居民获得均等化的基本医疗服务［8］；（2）受囿于基本公共卫生服务项目范围过大，加之现有的医疗卫生资源和服务能力无法满足基本公共卫生服务项目的要求［9］，造成基层医疗卫生机构压力过大和居民对基本公共卫生服务均等化满意度不高等现象，各地应结合经济水平和人群健康情况合理确定适宜本地的基本公共卫生服务包；（3）建立高素质卫生人员到基层的培养与吸引机制［10］，提高基层卫生人员的薪酬待遇，并以实践技能为核心，采取专项培养、脱产培训、宣传教育等措施不断提高基层卫生人员数量和质量，建立科学的激励机制和长效机制；（4）可以通过电视、手机、网络、宣传手册和开展相关知识讲座等方式加大宣传力度，使居民了解基本公共卫生服务项目内容和实施的益处，从而提高居民的认知度、信任度和参与度。

综上所述，本文运用TOPSIS法、秩和比法及二者模糊联合法对基本公共卫生服务质量进行综合评价，找出了影响基本公共卫生服务质量的因素，提出了针对性建议，为调整相关政策和提高服务质量提供了依据。研究结果表明TOPSIS法、秩和比法及二者模糊联合法能够比较科学、客观、全面地反映基本公共卫生服务情况，适宜在基本公共卫生服务质量评价中推广应用。

作者贡献：顾思雨、杨金侠负责文章的构思与设计；顾思雨、梁园园、章凯燕负责研究的实施与可行性分析、数据收集；顾思雨、梁园园负责数据整理、统计学处理、结果的分析与解释；顾思雨撰写论文；杨金侠负责论文的修订、文章的质量控制及审校，并对文章整体负责，监督管理。

本文无利益冲突。