改进离散S变换算法及其在槽波信号提取中的应用研究

吴 涛，杨思通，魏久传，施龙青，毛庆福，高学亮，刘 震

(1.山东科技大学 地球科学与工程学院，山东 青岛 266590；2.山东济矿鲁能煤电股份有限公司阳城煤矿，山东 济宁 272502)

采煤工作面内隐伏的大量前期难以精确查明的小规模地质构造严重影响现代化长距离快速采煤的安全生产，成为引发安全事故的重大隐患。槽波地震探测是当前高精度远距离探测工作面内隐伏的小规模构造的主要方法。煤层中激发的地震波在波阻抗差异较大的煤层与顶、底之间界面上产生强反射，能量较强的反射波在煤层内相互干涉形成了槽波。槽波信号在沿煤层传播，受传播路径上的断层、陷落柱、煤层厚度突变、夹矸石分布及剥蚀带等地质构造异常界面的反射或散射的影响，导致槽波的振幅、速度、相位、频率等属性发生变化。槽波地震探测方法正是利用槽波能量强、对构造界面敏感的特性来探测采煤工作面内隐伏的地质构造和内部异常[1]。在煤层槽波、煤层纵波、煤层横波、顶底板纵波、顶底板横波等各波型相互干涉混叠在一起的复杂地震数据中高精度保幅提取槽波信号是槽波地震勘探的关键基础。由于槽波的频散特性，其信号的高精度保幅提取是当前的一个难点。

短时傅里叶变换和小波变换虽然可以对信号进行时频分析，但各有不足。Stockwell于1996年提出S变换[2]，其结合了小波变换和短时傅里叶变换的优点，具有窗函数随频率变化自适应调节分辨率，在时频分析中具有低频处频率分辨率高，高频处时间分辨率高的的优势，是非平稳频散信号时频分析的优势方法[3]。但是Stockwell提出的S变换离散化公式中高斯窗函数参数固定不可调，导致传统离散S变换的时频谱的负频域部分失真。针对传统离散S变换负频率时频谱失真问题，高静怀提出了广义S变换[4]，广义S变换中的基本小波有4个可调参数，能够更加灵活的根据实际情况选择合适参数。但是其提出的广义S变换及后来研究者提出的其他类型广义S变换[5]并没有解决时频域中负频域失真问题。Carine Simon提出了一种新的S变换离散算法[6]，该算法更加贴合传统S变换的定义，能够保持S变换离散化之后高斯窗函数的对称性，解决了传统离散S变换负频域时频谱的失真问题，但是由于其离散化S变换是通过连续S变换直接转换得到的，其参数取值范围内含有负数，导致该离散化算法的最后一步不能直接利用快速傅里叶反变换进行计算。

1 S变换与反变换的理论基础

S变换(ST)是地球物理学家Stockwell于1996年提出的一种信号时频分析方法。在S变换中用高斯窗函数来代替小波基函数，又被称为“相位正交”的连续小波变换。式(1)和式(2)即为Stockwell提出的S变换公式[2]。

其中

式中，f为频率；t为时间；i为虚数单位；h(t)是要分析的信号；τ是时间平移因子，用于控制高斯窗在时间轴t上的位置；S(τ，f)为变换后得到的时频谱矩阵[7]；g(t，f)为高斯窗函数。

S变换的无损反变换见式(3)。

通过式(3)可将S变换得到的时频谱无损地反变换回原来的时间域信号。

S变换不同于短时傅里叶变换之处在于式(2)中高斯窗函数的幅值和宽度会随着频率f发生变化，频率f越高高斯窗函数的幅值就会越高，宽度就会越窄。所以S变换对低频信号的频率分辨率高，对高频信号的时间分辨率高，克服了短时傅里叶变换窗口幅值和宽度固定的缺陷。同时S变换的高斯窗函数g(t，f)表达式固定，克服了小波变换基函数杂多选择困难的缺点。S变换的数字信号处理需要将S变换离散化[6]，S变换的传统离散化表现形式见式(4)[2，8-10]。

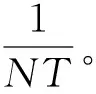
式(4)中的G[m，n]为离散化高斯窗函数的傅里叶变换，仍然为高斯函数形式，式(5)称之为离散频率域高斯窗函数。

与离散S变换对应的离散S反变换为：

2 改进的S变换离散化形式

Stockwell将连续S变换转换成离散S变换过程中其参数范围从-∞～+∞[5，14，15]变成0～N-1，没有考虑参数范围不同对高斯窗函数的影响，由于缺少负数部分，高斯窗函数G[m，n]失去对称性，造成应用式(4)进行S变换后其负频域部分的时频谱失真。因此Stockwell的离散S变换不关注负频域部分。如此一来，时域信号经传统离散S变换后，其时频谱的负频率部分的能量分布与原信号的能量在时间域和频率域分布不一致，因此，不能参与滤波处理和滤波后的反变换。只采用正频率部分的时频谱对信号在时频域进行滤波和滤波后的反变换。最终造成滤波保留信号幅度的损失。

为了保持S变换离散后的对称性同时能够直接利用快速傅里叶反变换进行计算，SIMON等人[5]，刘保童等人[14]和Chen[15]分别对该问题进行了研究。本文在以上研究的基础上提出了一种改进的离散S变换算法，以消除传统S变化因变量离散化取值范围的不同对高斯窗函数对称性的影响，新算法见式(7)。

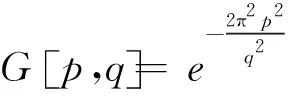
(7)

本文提出的改进算法是把m和n看成是离散频率域G[m，n]上的自变量，那么m和n小于N/2的部分可以看成是对应连续频率域G(m，n)上的自变量的正数部分，而m和n大于等于N/2的部分则可以看成是对应连续频率域G(m，n)上的自变量的负数部分，所以当m和n大于N/2时对应的连续频率域G(m，n)的自变量应该是m-N和n-N。所以在m和n大于N/2时将m-N和n-N代入离散频率域高斯窗函数G[m，n]中来修正该公式以此来保证G[m，n]的对称性。因此，改进算法变换后得到的信号时频谱的负频率部分不再失真，其在频率域的能量分布与正频率部分对称，因此可以直接参与滤波处理。滤波后可以采用传统的离散S逆变换算法重构不失真的保幅重构信号。

3 模拟槽波地震数据传统与改进离散S变换及其槽波信号提取

3.1 模拟槽波地震数据

建立了由顶板、煤层、顶板组成的三层含煤地层三维模型，模型中各层介质的弹性参数见表1。模型在X轴方向长度为150m；在Y轴方向上长度为80m；在Z轴方向上，顶板和底板厚度为5m，中间煤层厚度为10m。

表1 含煤地层模型介质参数表

应用150Hz雷克子波震源激发，采用如图1所示的激发和接收系统，震源和接收点均位于位于煤层下部，震源点和接收点坐标分别为(2m，20m，13m)和(148m，60m，13m)。

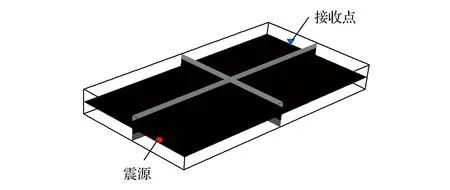
图1 槽波地震激发接收位置图

对三维煤层模型，采用图1的观测系统应用三维地震波动方程的的高阶交错网格有限差分模拟方法模拟了槽波地震垂直分量地震记录，如图2所示。槽波地震记录中槽波信号振幅远大于煤层横波振幅和顶、底板横波振幅，其在地震记录信号时域波列中分布在143～225ms之间，优势振幅集中在155～176ms之间。

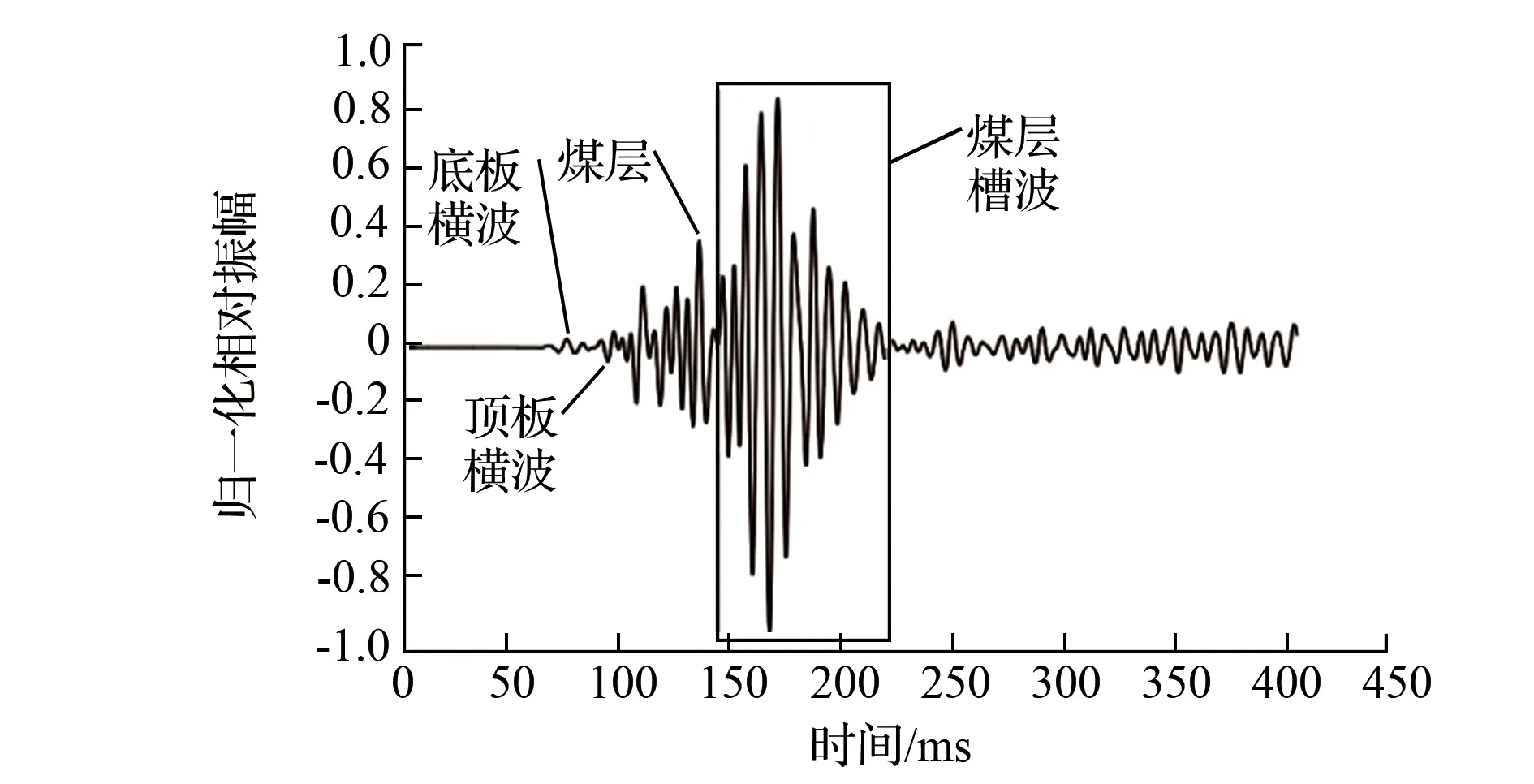
图2 模拟槽波地震记录

3.2 模拟槽波地震数据时频分析

对图2的模拟槽波地震记录进行传统的离散化S变换，其时频谱如图3所示，由图3可知负频率部分的时频谱发生严重畸变，能量在频率域不聚焦，成条带状分布在整个频率范围内；同时，负频率部分时频谱最大能量大约是正频率域部分时频谱最大能量的20倍。由于负频率域的时频谱畸变，其能量分布与模拟槽波地震记录能量在时频域中的实际分布不一致，因此，负频率域部分的时频谱不能参与从槽波地震记录中提取槽波信号的滤波和滤波后的反变换处理，其有用信号被浪费，只有不发生畸变的正频域部分时频谱可以参与槽波信号提取滤波和反变换。

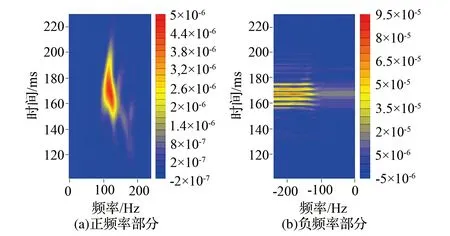
图3 模拟槽波地震记录传统离散S变换时频谱

对模拟槽波地震记录进行改进的离散S变换得到的时频谱如图4所示。由图4知离散S变时频谱负频率部分不再畸变，能量聚焦；正、负频率部分的时频谱能量范围相等，且关于0频率线对称分布，负频率部分的时频谱能量分布与正频率部分一样，与时域信号能量在时频域中的分布一致。如此一来，负频率域部分的时频谱可以参与槽波信号提取的滤波和滤波后的反变换处理，且在槽波信号提取滤波时正、负频率部分的时频谱可以采用相同绝对值范围的频率域滤波参数。

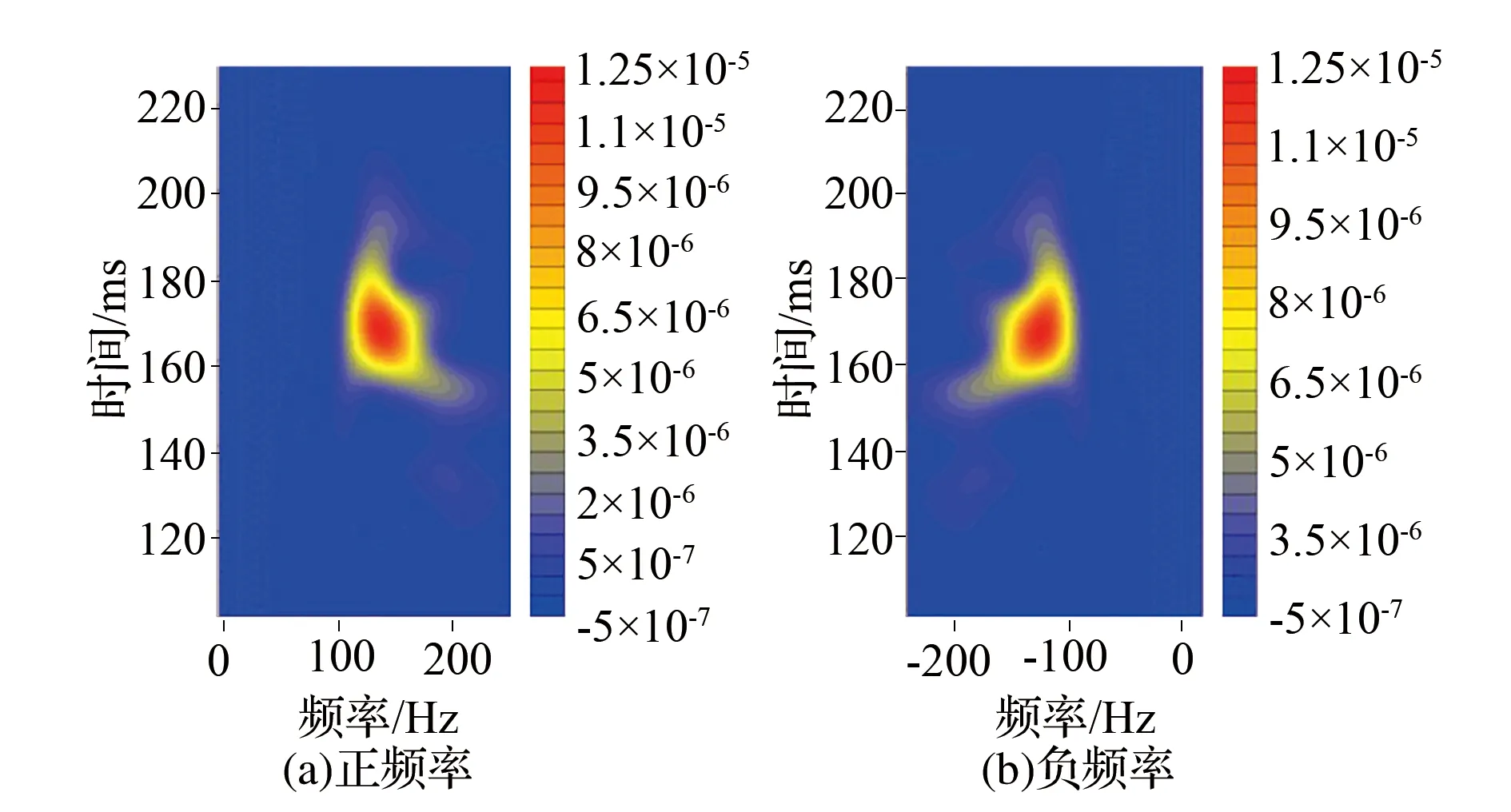
图4 模拟槽波地震记录改进离散S变换时频谱

对比图3和图4，传统离散S变换不发生畸变的正频率时频谱中的强能量槽波聚焦区域在时间域中分布范围超出了时域信号的时间分布范围，而在频率域中主能量的分布范围低于子波主频150Hz；而改进离散S变换时频谱中主能量的聚焦范围与时域信号在时间域中的分布范围较为一致，在频率域中的分布与子波主频150Hz较为对应。对比分析表明改进的离散S变换比传统的离散S变换更能较为真实的反映地震记录中的槽波信号在时频域中的能量分布，更有利于从地震记录中精确提取槽波信号。

3.3 模拟槽波信号提取

对传统离散S变换和改进的离散S变换的正、负频率时频谱从时间域和频率频率域采用高斯滤波器对模拟地震信号进行保留槽波信号的带通滤波处理，保留时域140～200ms范围内、频域90～230Hz绝对值范围内的时频域信号。然后将提取的时频域槽波信号反变换回时间域得到滤波后的时间域槽波信号[16]。两种离散S变换提取的时间域槽波信号与原模拟槽波地震记录对比如图5所示。

图5 模拟地震记录与提取的槽波信号对比图

图5中采用改进离散S变换时频谱提取的槽波信号最大振幅为模拟槽波地震记录中槽波信号最大幅度的97.97%，而采用传统离散S变换时频谱正频率部分提取的槽波信号最大振幅仅为模拟地震记录中槽波信号最大幅度的54.72%。图5表明应用改进的离散S变换时频谱进行槽波信号的滤波处理，可以有效的滤除顶、底板和煤层的体波信号，实现槽波信号的保幅提取。

4 改进离散S变换在实测槽波信号提取中的应用

4.1 阳城煤矿1311工作面槽波地震探测

阳城煤矿1311工作面所采煤层为3号煤，煤层厚度6.9m，顶板为巨厚致密中砂岩，底板为巨厚致密粉、细砂，顶板和底板地震波速和密度均明显大与煤层，槽波发育条件良好。工作面槽波透射探测范围长度为362.3m，宽度为183.5m，观测系统如图6所示。

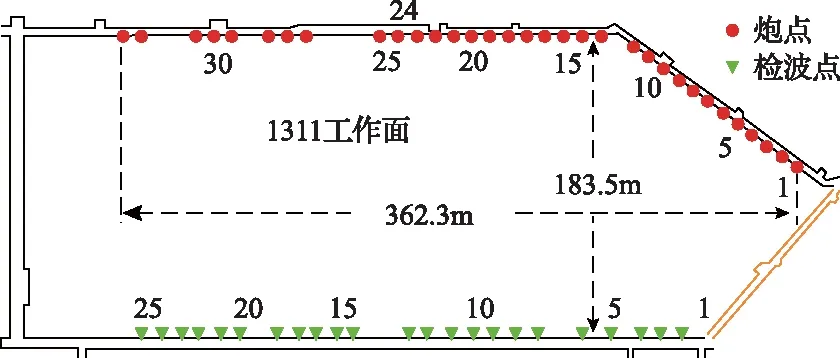
图6 1311工作面透射槽波探测观测系统

第1炮激发第1道接收的平行检波点所在巷道方向分量的地震记录如图7所示，炮检距为118m。

图7 1311工作面第1炮激发第1道接收的槽波地震记录

4.2 实测槽波地震数据的传统与改进离散S变换

分别为对图7的实测槽波地震记录进行传统离散S变换和改进离散S变换，分别得到两种变换的时频谱，如图8和图9所示。对比图8和图9表明，实测槽波地震信号改进离散S变换时频谱与模拟信号时频谱具有相同的正负频率对称特征，所以，改进离散S变换同样可以对实测槽波地震数据进行较为精确的时频域分析。

图8 实测地震记录传统离散S变换时频谱

图9 实测地震记录改进离散S变换时频谱

4.3 基于传统与改进离散S变换的实测槽波信号提取

分别对实测地震记录的传统离散S变换正频率部分时频谱(图9a)和改进的离散S变换的正、负频率时频谱(图9)从时间域和频率频率域采用高斯滤波器进行保留槽波信号的带通滤波处理，保留时域160～180ms范围内、频域100～250Hz绝对值范围内的时频域信号；然后将提取的时频域槽波信号反变换回时间域得到时间域实测槽波信号。从两种离散S变换时频谱中提取的时间域槽波信号与原实测地震记录对比如图10所示。图10表明改进的离散S变换可以用于实测槽波信号最大振幅几乎无能量损失的保幅提取。

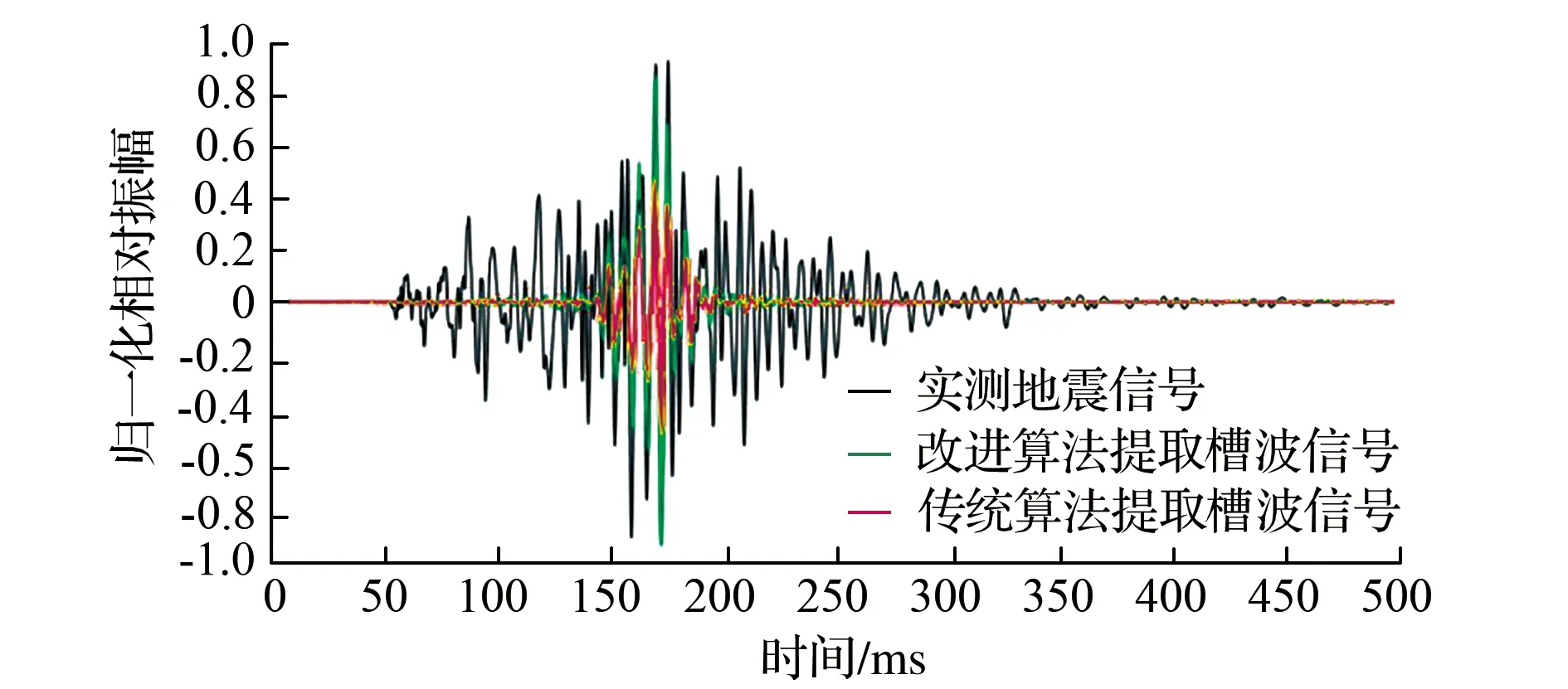
图10 原始实测槽波地震信号与提取槽波信号对比图

对1311工作面实测槽波地震数据的第25炮所有25道地震记录(图11)进行基于改进离散S变换时频谱滤波的的槽波信号提取得到第25炮槽波信号地震记录，如图12所示。对比图11和图12表明，对基于改进离散S变换的时频谱滤波，可以较为干净的滤除实测槽波地震记录中煤层体波信号(纵波和横波)，精确实现复杂槽波地震数据中槽波信号的保幅提取。通过对实测槽波地震数据的应用表明相对于传统的离散S变换，改进的离散S变换可以实现在时频域中对槽波地震数据进行体波和煤层槽波分离，通过对改进离散S变换时频谱时频域滤波可以完成在槽波地震数据中精确保幅地提取槽波信号。

图11 实测第25炮原始槽波地震记录

图12 基于改进离散S变换提取的第25炮槽波信号记录

5 结 论

1)针对传统离散S变换负频率时频谱能量分布畸变，导致只有正频率时频谱可以用于槽波信号时频域滤波提取，造成提取的槽波信号幅度大幅度损失的缺点。本文提出了改进的离散S变换算法，该方法保持了离散化高斯函数的对称性，使得时频谱负频率部分不再畸变，正负频率域的时频谱能量相当且关于0频率轴左右对称。改进的离散S变换的正、负频率时频谱可以采用相同绝对值范围的频域滤波参数进行槽波信号的滤波和S反变换，实现槽波信号的保幅提取。

2)通过对模拟槽波地震数据和实测槽波地震数据的槽波信号提取应用效果分析，验证了改进的离散S变换时频谱在时间域和频率域的能量分布均与原始信号能量在时间域和频率域中的分布较为一致，克服了传统离散S变换正频率时频谱槽波信号能量在时间域中分布范围扩大，在频率域中分布范围缩小的不足。

3)通过对阳城煤矿1311工作面实测槽波地震数据的槽波信号分提取应用，验证了改进的离散S变换在槽波信号保幅提取中的优势和适用性。