三维趋化系统全局弱解的存在性和渐近稳定性
唐浩怡,彭红云
(广东工业大学 数学与统计学院,广东 广州 510520)
关于抛物−双曲型系统解的适定性(局部和全局)和渐近稳定性的数学研究很多,但这些研究大多集中于连续初值[1-4]。相比连续初值,不连续初值的研究难度更大。本文考虑以下PDE-ODE趋化模型

在不连续初值下全局弱解的适定性和大时间行为。该模型描述了肿瘤血管生成过程中血管内皮细胞生长信号因子VEGF(Vascular Endothelial Growth Factor)和血管内皮细胞之间的相互作用[5]。u(x,t)和c(x,t)分别代表血管内皮细胞的密度和血管内皮细胞生长信号因子的浓度。参数 ξ>0是衡量趋化强度的趋化系数,µ代表生长信号因子的降解率。通过Cole-Hopf变换[6]

系统(1)可变为抛物−双曲型方程
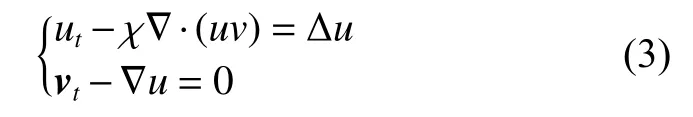
系统(3)满足初始条件和无穷远状态

对于一维的趋化抛物−双曲型系统(3)已经有了大量的研究。首先,一维行波解的存在性和稳定性可参考文献[7],关于解的整体存在性可参考文献[8-10],关于有界区间上解的存在性可参考文献[4,11]。对于多维全空间 R2,文献[12]讨论了关于有界区域上平面行波的非线性稳定性。对于高维情形,当初值接近常数平衡态时,关于经典解爆破准则的研究可参考文献[13-14],在文献[13]中也讨论了当,∈Hs(Rd)(d∈Z+),很小时,解的大时间行为。在初值正则性高的情况下,当小,解的代数衰减率可以进一步在文献[1]得到。当∈H2(Rd)(d∈Z+)且很小时,文献[2]讨论了在 Rd(d=2,3)上解的整体存在性和时间衰减速率。以上的结论都是基于初值的高正则性和Hs(s∈N,s≥1)模小的情况下,所得到的解都是强解。而关于不连续初值的研究难度更大,成果不多,因为 ∇v的可积性在连续初值的分析[1-2,13]中有关键性地位并且很容易得到。由于初值的正则性低,难以得到 ∇v的可积性,只能期望得到v的Lp可积性。在文献[15-16]中分别讨论了在R 和R2上全局弱解的适定性和渐进稳定性。本文期望在R3空间讨论模型(3)全局弱解的稳定性。其中,本文引入了“有效粘性通量”的工具来处理需要的能量估计和v的正则性。由Navier-Stokes方程组相关研究[17]的启发,式(3)的第一个等式可改写为=∇·F,“有效粘性通量”F可定义为

那么,式(3)的第二个等式可化为vt=−χuv+F。利用有效粘性通量,可以处理初始值正则性较低带来的困难。因为χ 和对本文的分析没有实质影响,以下不妨设,首先引入弱解的定义。
定义1若(u,v)可积且对于任意可测函数,有
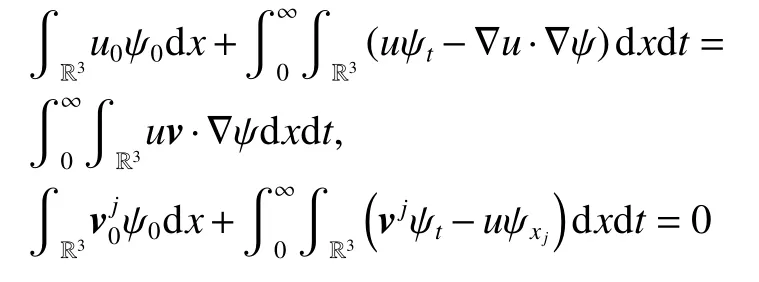
那么(u,v)是系统(3)~(5)的弱解,式中:j=1,2,3,ψ0(x)=ψ(x,0)。下面介绍本文的主要结论。
定理1假设4

并且使得式(8)中的渐近行为成立:

式中:2 定理1的初值条件表明(u0,v0)可以是不连续的,这给分析带来了很多困难。为了证明定理1,首先对初值进行磨光,在磨光后的初值下得到全局光滑解(uδ,vδ),然后当极限δ→0时,得到系统(3)~(5)的弱解。本文证明的关键点在于得到与磨光参数 δ无关的全局先验估计。由于以往处理连续初值的理论框架不能完全解决本文中的问题,所以需要引入“有效粘性通量”F来获得关于δ 的一致估计。相比于二维的研究,有一些非线性项在三维情形下更难处理,这需要一些新的技巧来处理这些非线性项,从而得到关于δ的一致先验估计。 介绍一些记号: (1)Hk(R3)表示在R3上的k阶Sobolev空间,范数形式为,L2是L2(R3)的缩写。 (2)θ0=∥u0−1∥2+∥v0∥2,在文中θ0是一个很小的数,不失一般性设θ0<1。 以下介绍Cauchy问题(3)~(5)光滑解的局部存在性和爆破准则。 引理1[13]令。存在使得Cauchy问题(3)~(5)存在唯一的解(u−1,v)∈L∞((0,T∗],Hs(Rd)),d∈Z+。 引理2[14]令。如果(u,v)是引理1在最大有效时间T∗>0上唯一的局部解,那么当 时,解(u,v)可以往T∗>0以外延拓。 在这种变换下,式(6)中定义的“有效粘性通量”F可写为 引理3[16]令是系统(10)的光滑解,则存在一个正常数C,使得 引理4[18]令1≤q,r≤∞,r∈(0,p),1 在这一节中,本文拟在磨光初值下构造近似解来证明定理1。令,其中,=u0−1,jδ是标准磨光核。然后考虑近似系统 通过引理1,可以得到满足初值(16)~(17)的近似系统(15)的解的局部存在性。然后,将在以下引理中证明近似解满足一些与参数δ 无关的全局先验估计。简单起见,仍然用表示近似解。令T>0是给定时间,是系统(15)在R3×(0,T]上的光滑解。设σ=σ(t)=min{1,t},定义 接下来,将利用先验假设的方法得到系统(15)~(17)光滑解的先验估计。假设对于任意t∈[0,T],光滑解满足 式中:M和θ0的定义与定理1中的相同,η0定义为 最后,将在式(19)下获得(15)~(17)的整体解,从而封闭先验假设。下面从的L2估计开始。 引理5在定理1的条件下,若系统(15)~(17)的光滑解满足式(19),则满足不等式 证明对式(15)的第一个方程和第二个方程分别乘以和v,再把所得结果加起来并积分可得 由Hölder,Cauchy-Schwarz不等式和式(14)得 把式(23)代入式(22)可得 对式(24)在[0,t]上积分,利用式(17)~(19)有 引理6在定理1的条件下,若系统(15)~(17)的光滑解满足式(19),则满足不等式 式中:σ=σ(t)=min{1,t}。 证明第一步:对式(15)的第一个方程乘以,将所得结果在R3×[0,T]上积分得 对于式(26)右边的第二项,利用 Cauchy-Schwarz 不等式、式(14)、式(19)和式(21)可得 式中的常数λ >0将在后面给定。对于式(26)右边的最后一项 由Cauchy-Schwarz不等式和0≤σ≤1得 由系统(15)的第二式可得 因此,有 由Cauchy-Schwarz不等式、Hölder不等式、式(14)、式(18)和式(19)有 再由式(11)和式(14)得 由式(19)、式(33)和0≤σ≤1,可得 由θ0<1,η0>0,式(11)、式(14)、Cauchy-Schwarz不等式和Young不等式得 由式(13)和Hölder不等式有 由式(18)、式(19)、式(35)、式(36)、Young不等式和Cauchy-Schwarz不等式可得 由Young不等式、式(18)和式(19)得 然后,把式(37)和式(38)代入式(34),取 θ0足够小使得,由式(20)得 由式(32)和式(39)得 对式(31)右边的最后一项,由Cauchy-Schwarz不等式,式(14),式(19)和插值不等式可得 把式(40)和式(41)代入式(31),取 θ0足够小使得,有 联合式(29)可得 结合式(29)得 式(42)取θ0足够小使得≤1, 引理7在定理1的条件下,若系统(15)~(17)的光滑解满足式(19),则满足不等式 而且对于任意t∈(σ(T),T],有 引理8在定理1的条件下,取,若系统(15)~(17)的光滑解满足式(19),则满足 证明由式(11)和vt=得 对式(44)乘以|v|2v,再对结果积分有 对式(45)在[σ(T),T]上积分,由式(43)得 由插值不等式和式(19),对任意2 由Young不等式有 由式(14)得 由式(25)和式(35)得 由式(19)、式(25)、式(36)、Cauchy-Schwarz不等式、Young不等式和式(39)得 把式(52)代入式(48)得 另一方面,当0≤t≤σ(T)时, 因此, 引理9在定理1的条件下,若系统(15)~(17)的光滑解满足式(19),则满足不等式(54) 参考文献[16]的证明方法,可以得到关于 δ的一致估计: 同时,有 再由Aubin-Lions-Simon 引理[15],取一个子序列,当δ→0时,可得在C([0,∞),H−1(R3))中,vδ(·,t)强收敛于v,在(u,v)中uδ(·,t)强收敛于u(·,t),在L2([0,∞),L2(R3))中,∇uδ(·,t)弱收敛于 ∇u(·,t)。 上述结果可知(u,v)是系统(3)~(5)的弱解。参考文献[16]的证明方法,本文可以证明式(8)。定理1证明完毕。1 预备引理



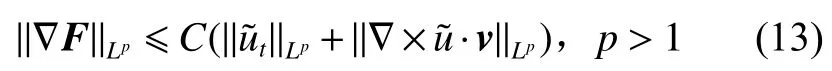

2 近似解的先验估计



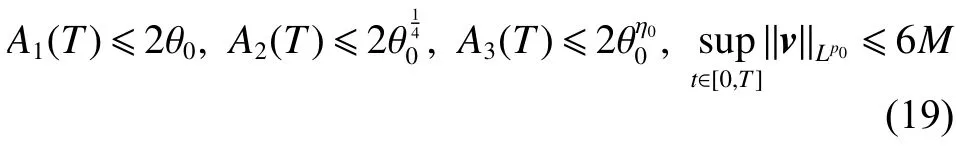

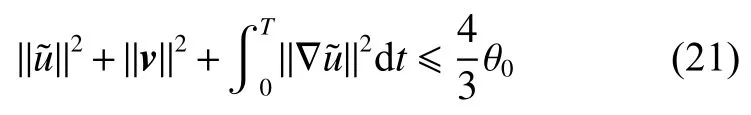
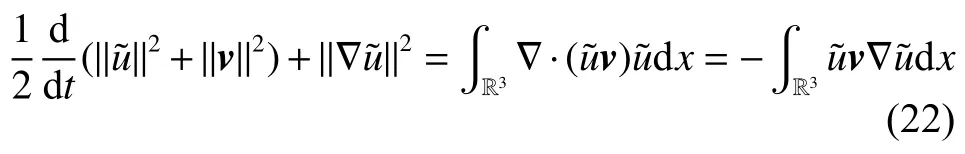

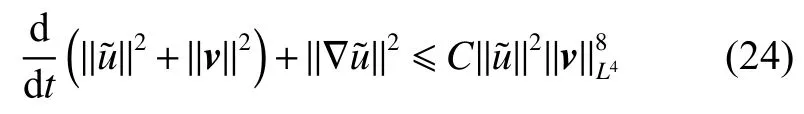
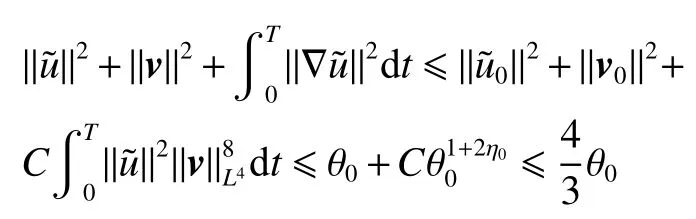


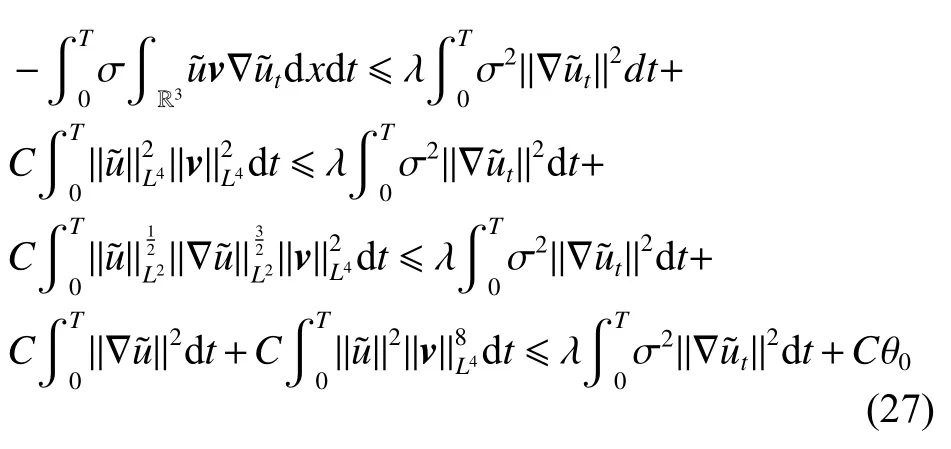
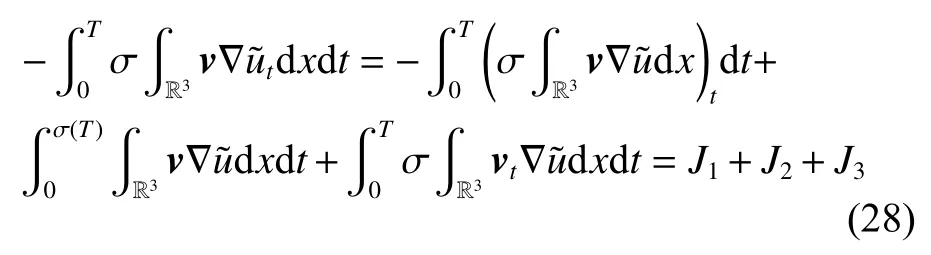
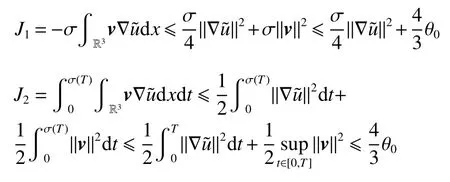

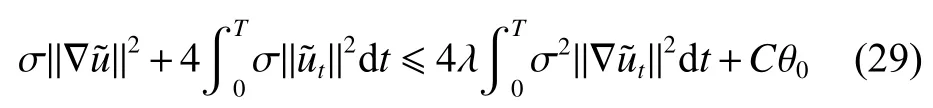
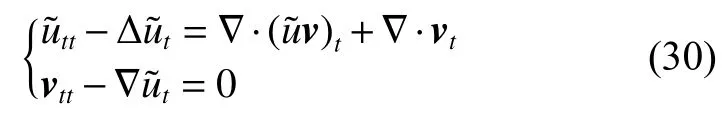
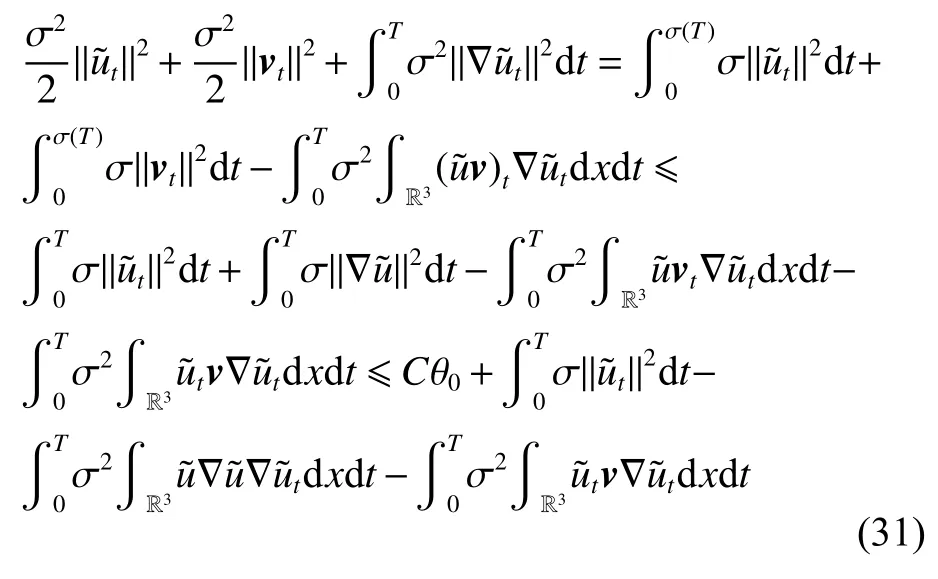
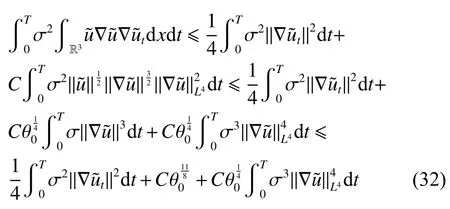
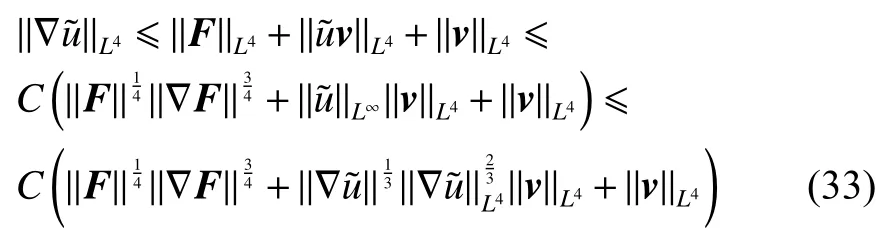
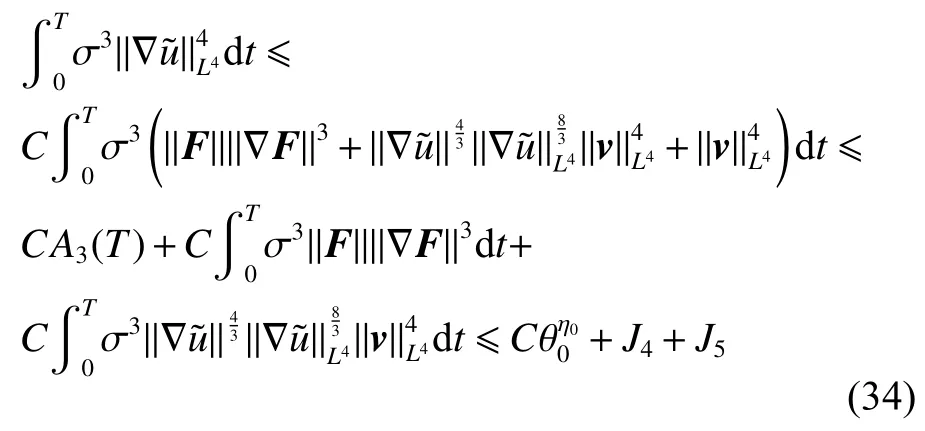

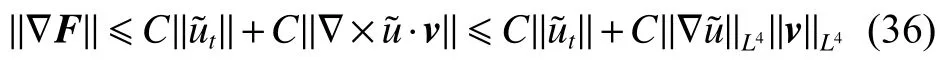

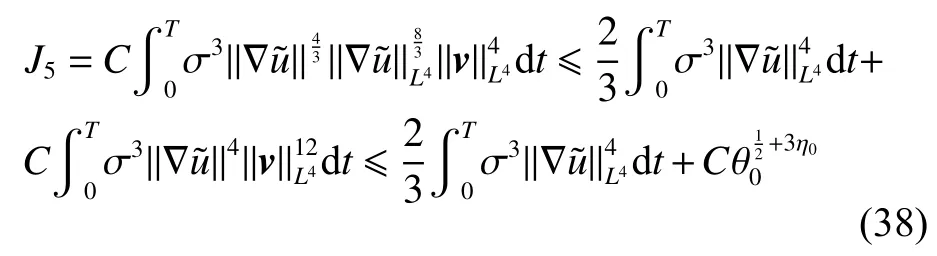


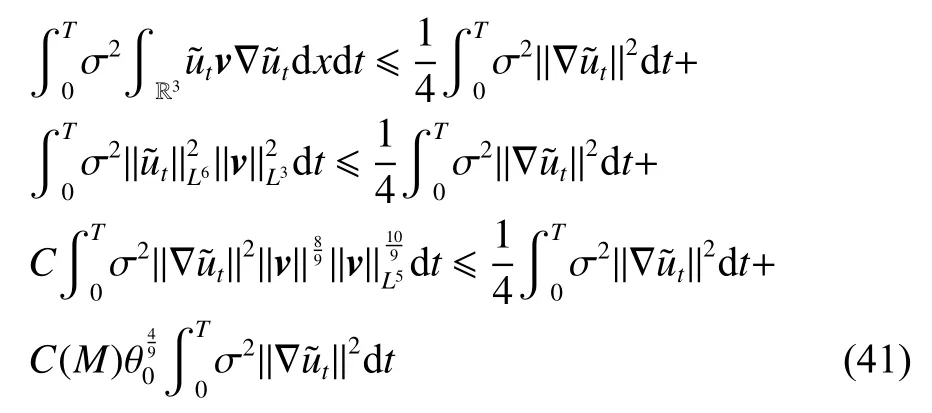
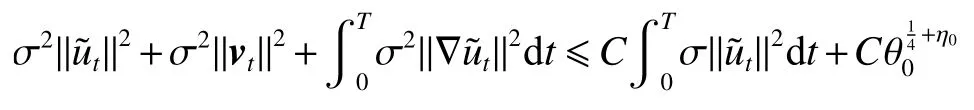
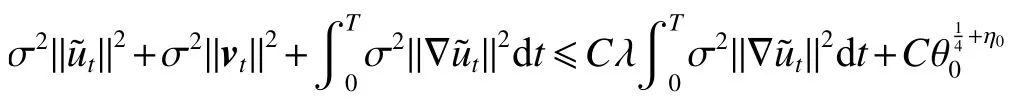
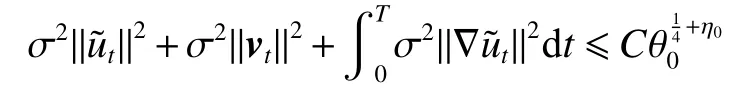


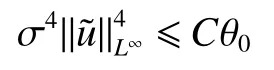
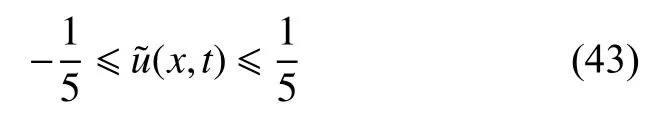



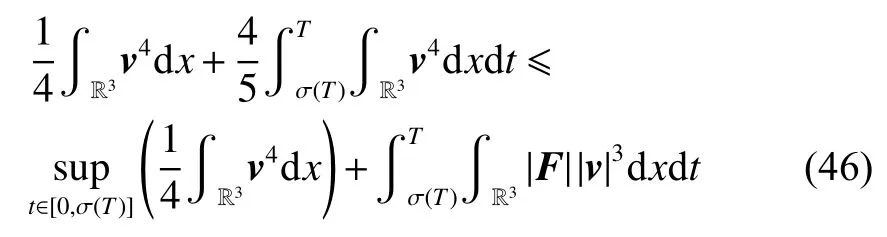
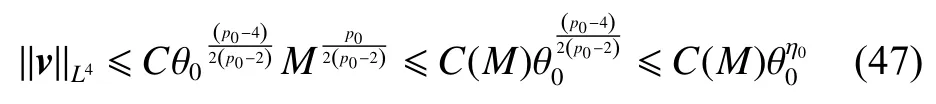

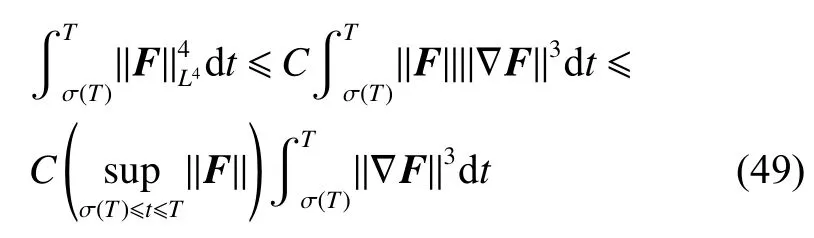


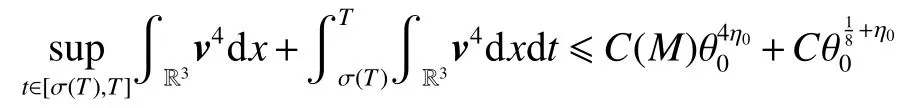

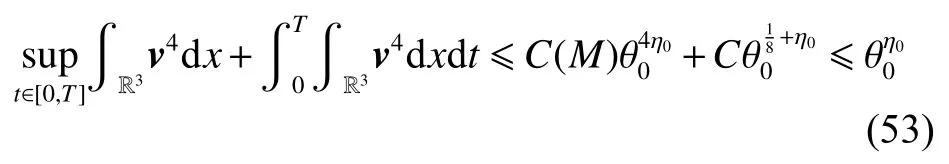

3 定理1的证明