基于线性回归理论的智能交通算法

李志鹏

（江西财经大学，江西 南昌 330013）

0 引 言

随着经济的快速发展，汽车越来越多，交通压力越来越大，尤其是大城市上下班高峰期，在某些重要的交通路口，时常出现横、纵向车交叉在一起的情况，造成长时间的拥堵。基于上述问题，本文提出了一种基于线性回归理论的智能交通分析算法。若出现拥堵情况，可将当前状况通过车载电视或者收音机播放给汽车听众，便于汽车司机及时做出处理。

智能交通算法可较好地解决交通拥堵情况，减少人工干预，很多人也对智能交通提出了不同的见解。罗素瑾提出了一种基于静态图片或动态视频检测目标对象的方法[1]，卢东祥分析了静态与动态路径规划算法的优劣势，用路径规划算法的未来研究趋势及方法[2]，郭洋利用数据挖掘、优化和改进交通流量预测算法[3]，徐成对交通拥堵问题提出了车流量检测的不定顺序控制算法研究[4]。本文在线性回归理论的基础上设计算法，可改善交通拥堵问题，节省通行时间。

1 线性回归相关理论

线性回归理论是基于一次函数的特征，找出两个变量之间的关系，通过数学方式解决实际问题。线性回归模型表达式为y=bx+a，其中，b为斜率参数，a为截距参数。对于n个数据点(x1,y1)，(x2,y2)，…，(xn,yn)，通过式（1），计算出相应的斜率参数b^和截距参数a^[5-6]：

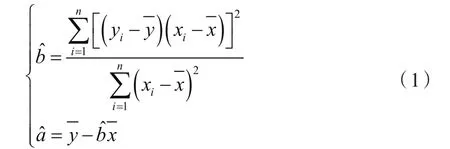
2 算法设计

以十字路口为例，对当前路口进行编号。随机挑选相向行驶的两个路口编号分别为1，2，另外相向行驶的两个路口编号分别为3，4。以正前方直行编号为1，左转编号为2。通过汽车计数器，检测当前行驶车道由红灯变绿灯期间的平均汽车数量，公交车和大货车均以普通汽车的两倍计数，计算当前各个车道的平均等待车数p，同时记录当前车道由红灯变绿灯等待的时间Td。将Td均分成6份，0-1/6Td的车辆作为当前行驶车道第1个纵坐标，0-2/6Td的总车辆作为当前行驶车道第2个纵坐标，0-3/6Td的总车辆作为当前行驶车道第3个纵坐标，以此类推，可得当前行驶车道第4，5，6个纵坐标。

将 1，2，3，4，5，6作为相应的横坐标，用yuvw作为相应的纵坐标，其中，u=1,2,3,4表示路口编号，v=1,2表示行驶方式，w表示0-t/6Td(t=1,2,3,4,5,6)的总车辆。如路口编号1的正前方直行形成6个坐标分别为(1,y111)，(2,y112)，(3,y113)，(4,y114)，(5,y115)，(6,y116)，路口编号1的左转形成的6个坐标分别为(1,y121)，(2,y122)，(3,y123)，(4,y124)，(5,y125)，(6,y126)。

同理，路口编号分别为2，3，4的正前方直行和左转形成的坐标分别为：(1,y211)，(2,y212)，(3,y213)，(4,y214)，(5,y215)，(6,y216)；(1,y221)，(2,y222)，(3,y223)，(4,y224)，(5,y225)，(6,y226)；(1,y311)，(2,y312)，(3,y313)，(4,y314)，(5,y315)，(6,y316)；(1,y321)，(2,y322)，(3,y323)，(4,y324)，(5,y325)，(6,y326)；(1,y411)，(2,y412)，(3,y413)，(4,y414)，(5,y415)，(6,y416)；(1,y421)，(2,y422)，(3,y423)，(4,y424)，(5,y425)，(6,y426)。

由式（1）计算路口编号1，2，3，4的斜率参数buv，其中，u=1,2,3,4表示路口编号，v=1,2表示行驶方式，如路口编号1的正前方行驶斜率参数为b11，左转斜率参数为b12。判断斜率参数buv，若求得对应的斜率参数b小于等于0，则呈现负相关，表示车辆少，不做处理，按照当前设置的红绿灯时间通行。如果斜率参数b大于0，则按以下步骤操作。

（1）判断n次等待的时间的buvn，n=1,2,3,…表示第n次，并按照式（2）求h1：

式中：b11i是编号为1的直行的第i（i=1,2,3,…,n）次斜率参数，b12i是编号为1的左转的第i次斜率参数。同理，按照式（3）分别求h2，h3，h4，h5，h6，h7，h8。

（2）比较hj(j=1,2,3,…,8)的大小，若h2+h4≤h1+h3，表明1，2号路口的直行车道的车辆数相近，1，2号路口的左转车道的车辆数相近，则1，2号路口直行车道同时开通，1，2号路口左转车道同时开通。若h2+h4＞h1+h3，表明1，2号路口各自直行及左转车道车辆数均相近，则1号直行和左转同时开通，2号直行和左转同时开通；同理，若h6+h8≤h5+h7，则3，4号车道直行车道同时开通，3，4号左转车道同时开通。若h6+h8＞h5+h7，则3号直行和左转同时开通，4号直行和左转同时开通。检查hj(j=1,2,3,…,8)，如果发现其中某个hj(j=1,2,3,…,8)值过大，则告知交通部门，当前时间该行驶方式过于紧张，请及时处理。

（3）判断n次等待时间中pn(n=1,2,3,…)的增长值，如果pn(n=1,2,3,…)呈现增长趋势，则当前绿灯时间需要增加，需增加时间的计算公式为

式中：p1为当前计数的第1次等待对应车道车辆数平均值，pn为第n次等待对应车道车辆数平均值。为了表达方便，引入取整函数，如[1.02]=1，且以秒为单位，如果T+持续增加，则当前绿灯通行时间需设定上限值Tu，并通知交通部门，当前时间该通行方式过于紧张，请及时处理。

通过上述步骤，便于计算节省时间的通行方式，并作出相应的处理方案。具体流程如图1所示。

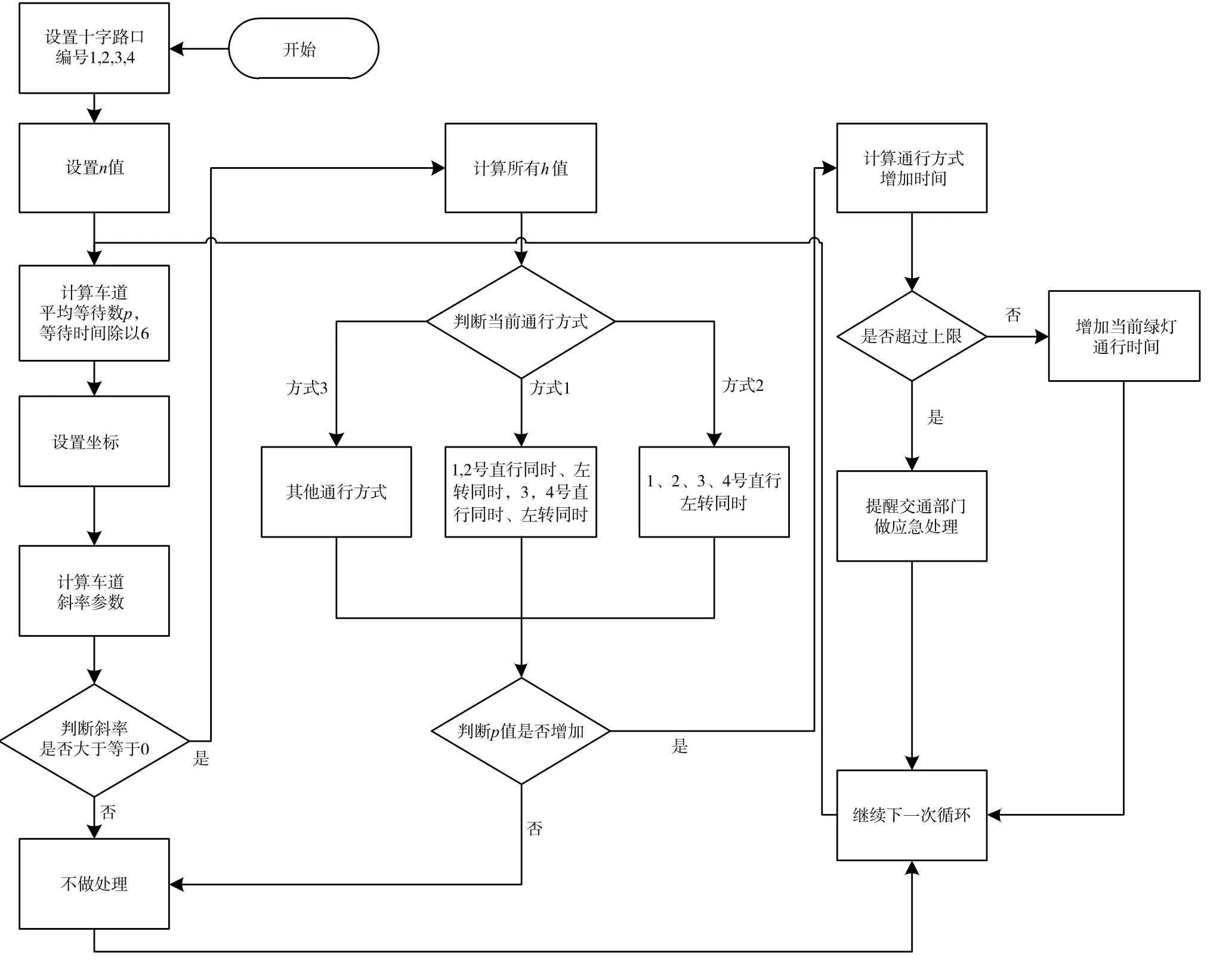
图1 数据处理流程图

3 算法结果

以某十字路口上午八点的数据为例，设置次数n=2，单个行驶方向绿灯上限为60 s，1号路口第1次直行车道坐标为（1，2），（2，3），（3，5），（4，7），（5，8），（6，9），1号路口第 1次左转车道坐标为（1，1），（2，2），（3，3），（4，4），（5，5），（6，7），2号口第1次直行车道坐标为（1，2），（2，4），（3，5），（4，7），（5，9），（6，10），2 号路口第 1次左转车道坐标为（1，1），（2，2），（3，4），（4，4），（5，5），（6，7），3号口第 1次直行车道坐标为（1，2），（2，4），（3，5），（4，8），（5，8），（6，10），3号口第1次左转车道坐标为（1，0），（2，1），（3，3），（4，4），（5，5），（6，6），4号口第 1次直行车道坐标为（1，0），（2，3），（3，5），（4，6），（5，8），（6，11），4号路口第1次左转车道坐标为（1，0），（2，1），（3，3），（4，4），（5，5），（6，5）；1号口第2次直行车道坐标为（1，3），（2，5），（3，7），（4，8），（5，10），（6，12），1 号路口第 2 次左转车道坐标为（1，2），（2，4），（3，6），（4，7），（5，9），（6，10），2号口第2次直行车道坐标为（1，1），（2，4），（3，7），（4，9），（5，12），（6，14），2号路口第2次左转车道坐标为（1，1），（2，2），（3，4），（4，7），（5，8），（6，9），3 号口第2 次直行坐标为（1，2），（2，4），（3，6），（4，8），（5，10），（6，12），3号路口第2次左转车道坐标为（1，2），（2，3），（3，5），（4，7），（5，9），（6，10），4号口第2次直行车道坐标为（1，3），（2，4），（3，6），（4，8），（5，10），（6，13），4 号路口第 2 次左转车道坐标为（1，1），（2，2），（3，3），（4，5），（5，7），（6，8）。对应数值的斜率参数如表1和表2所示。

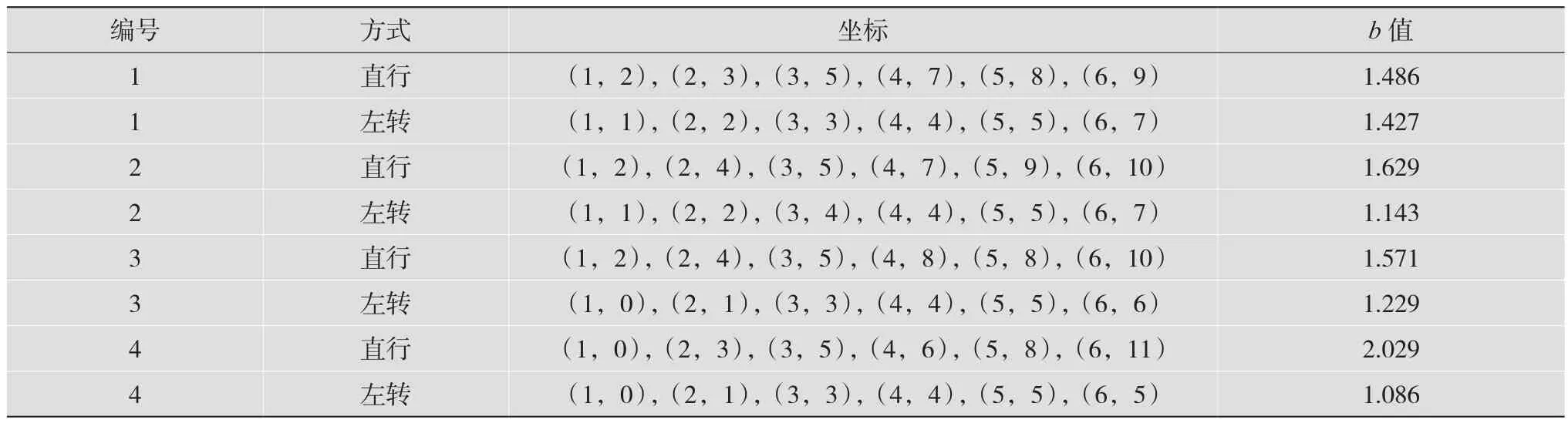
表1 第1次数据坐标、斜率参数

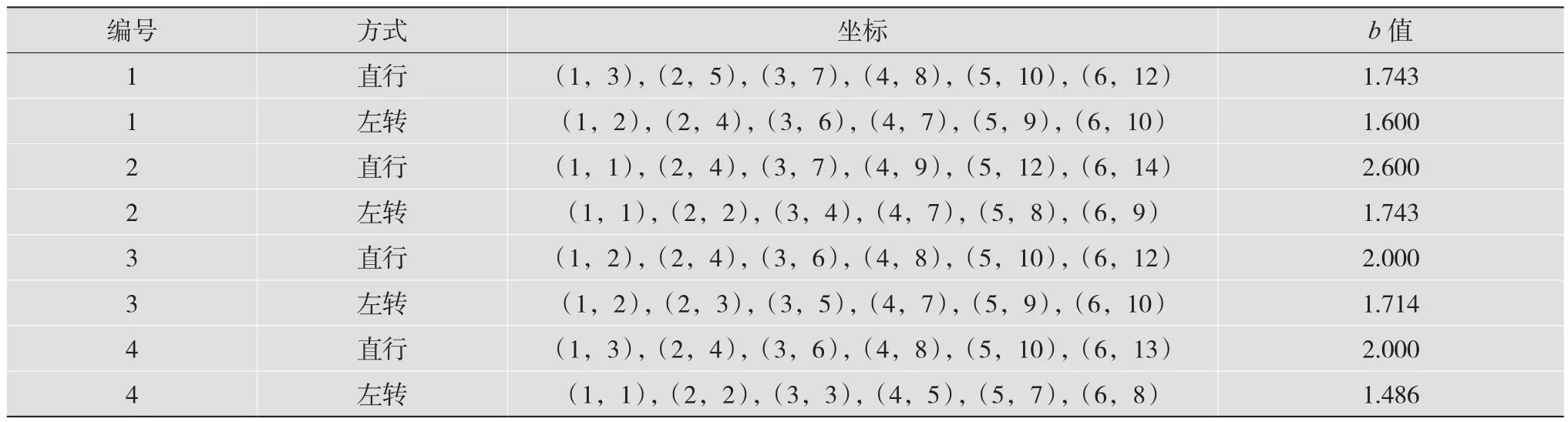
表2 第2次数据坐标、斜率参数

形成的buvn，hj及hj值比较如表3所示。

表3 buvn，hj及hj值的比较

根据表3，若h2+h4＜h1+h3，则 以 1，2号 车道直行同时开通，1，2号左转同时开通；若h6+h8＜h5+h6，则以3，4号车道直行同时开通，3，4号车道左转同时开通。每个车道增加的绿灯时间如表4所示。

根据表4，当车辆增多时，绿灯时间随之增加，但不能超过限定值。

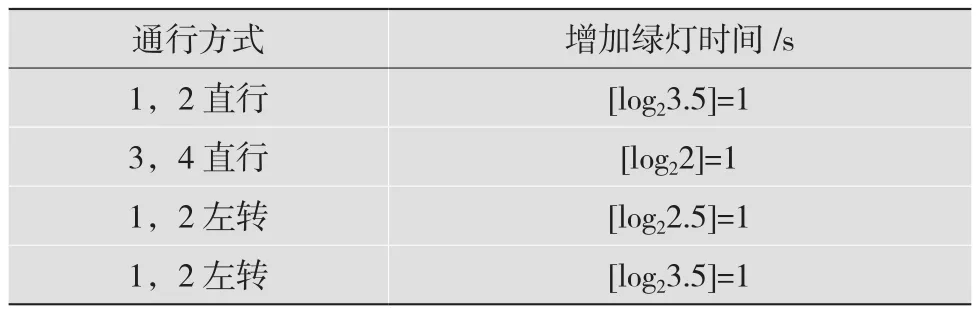
表4 每个车道绿灯增加时间

4 结 语

本文基于线性回归理论，计算各个值的斜率参数，进而求得hj(j=1,2,3,…,8)，最后通过比较hj的大小，判定合适的通行方式。用此方法可有效地动态调节绿灯时间，有效防止因车辆过多且通行时间太短而导致车辆拥堵情况。当然，此方法也有不足之处，对于5个以上的路口，需要调整算法。