某型直升机减速器宽带声源定位方法研究＊

孙宇星 陈亚农 何刘海 蒋燕英

（1.中国航发湖南动力机械研究所，湖南株洲 412002;2.中国航空发动机集团航空发动机振动技术重点实验室，湖南株洲 412002)

基于传声器阵列的声源识别技术是在声测量过程中加入算法后，对测量到的声信号进行处理并最终将声信号可视化的一种先进技术。工程机械的噪声频带往往较宽，所以能适用于宽频带噪声的声源识别技术成为了该领域的研究热点。

1980年Williams等人[1-3]提出的近场声全息技术（NAH，Near- fi eld Acoustic Holography）是目前国内外最常用的一种基于声阵列的声源识别技术。在这之后，Koopmann等人[4-5]又基于NAH原理以及波叠加法提出了基于等效源法（Equivalent Source Method, ESM）的 NAH，这种技术因其源面适应性好、计算效率高等优点而成为了NAH研究中的一大亮点。Kim等人[6]利用Tikhonov正则化来解决等效源法求解过程中的不适定性，之后又有学者提出了L-curve法[7]和广义交叉验证(GCV)法[8]来确定正则化参数，但这些算法适用的频带都较窄。在2016年，Hald[9]将ESM与压缩感知法相结合，提出了一种宽带声全息法（WBH, Wideband Acoustic Holography），该方法使用一组基函数来假设稀疏声场，并在迭代过程中加强稀疏性来求解声场信息，这使得计算效率被提高，此外，还有效拓宽了声源识别测量频带。

本文首先介绍了ESM法与WBH法的基本原理，接着运用ESM法与WBH法对某直升机减速器的特征频率进行仿真，将结果对比分析后验证了WBH法对于宽频带噪声声源识别的有效性与优越性。

1.ESM法原理

根据ESM法的基本原理，按照图1布置声源、等效源面、重建面和全息面（测量阵列），并假设传声器个数为M，等效源个数为N。

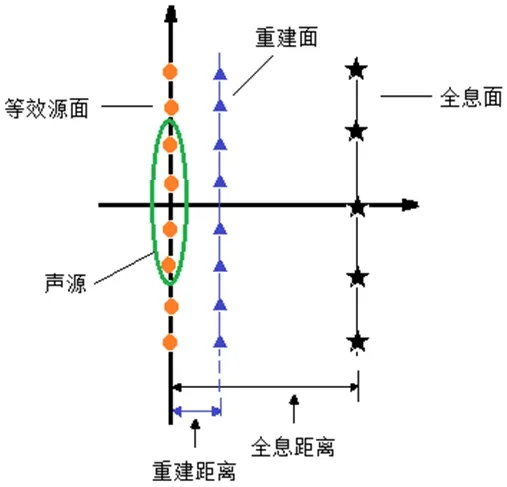
图1 ESM法原理示意图

全息面测量声压p（M×1）、等效源强度q（N×1）与传递矩阵G（M×N）可以写成矩阵形式为：

2.WBH法原理

WBH法对ESM法得到的结果进行了迭代优化，该种方法首先对得到的声压向量P进行互谱运算后得到其全互谱矩阵C，再进行特征值分解：

V=[v1,v2,…vμ…vM]为特征向量 ；S=[s1,s2,…sμ…sM]为特征值对角矩阵，μ=1,2,…,M。通过特征值分解可获得互谱矩阵每阶主分量，也就是传声器测得声压的不相干成分，可表示为：

通过对每一阶主分量进行迭代求解可以得到其相应的等效源强度。

先定义某一阶主分量的残余向量r和二次残余函数F：

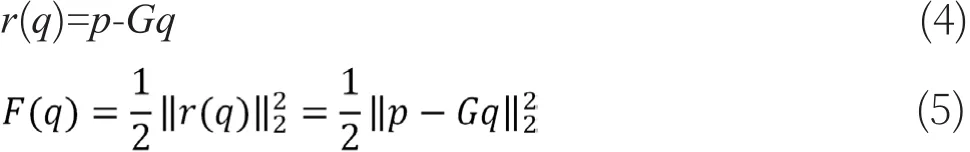
接下来运用最速下降法求解，当迭代至第k次时其搜索步长为：

其中，wk为负梯度方向；ak为搜索步长；gk=Gwk为辅助向量。

当迭代到第k+1次，等效源强向量可表示为：

式中，α∈[0.5,1.0]为松弛因子。接下来设置阈值滤波过程中的阈值函数Tk如下：

其中，Dk为阈值滤波动态范围，|qk+1,max|表示qk+1所有元素中的最大幅值，阈值滤波过程为：

通过式（11）的阈值滤波可以对旁瓣鬼影的产生进行持续抑制。Dk也需跟随迭代过程不断更新：

其中，ΔD表示动态范围的迭代步长。为了防止阈值滤波失效，需要选取一个动态范围上限Dmax，对Dk设置的迭代停止条件为：

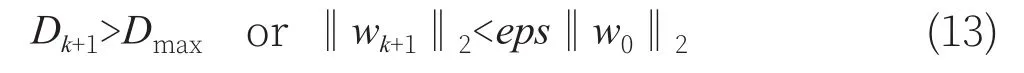
式中，eps为容差，一般初始化设置中有

通过上述一系列公式可以迭代计算出每一阶主分量对应的等效源强度，最终重建声场的总等效源强度为：

3.某型直升机右头部减速器结构及其振动特征频率

减速器是直升机传动系统的核心部分，它可以将发动机输出的每分钟几千甚至上万的高转速降低为每分钟几百甚至一百多的低转速[10]，再通过输出轴传递给旋翼，此外，主减速器还能将多台发动机功率合并后按比例分配给主旋翼、尾桨和各个附件，以保证直升机正常工作。

图2为某型直升机中的右头部减速器结构图，本文借鉴该减速器中几个振动特征频率，如表1所示。

图2 右头部减速器结构图

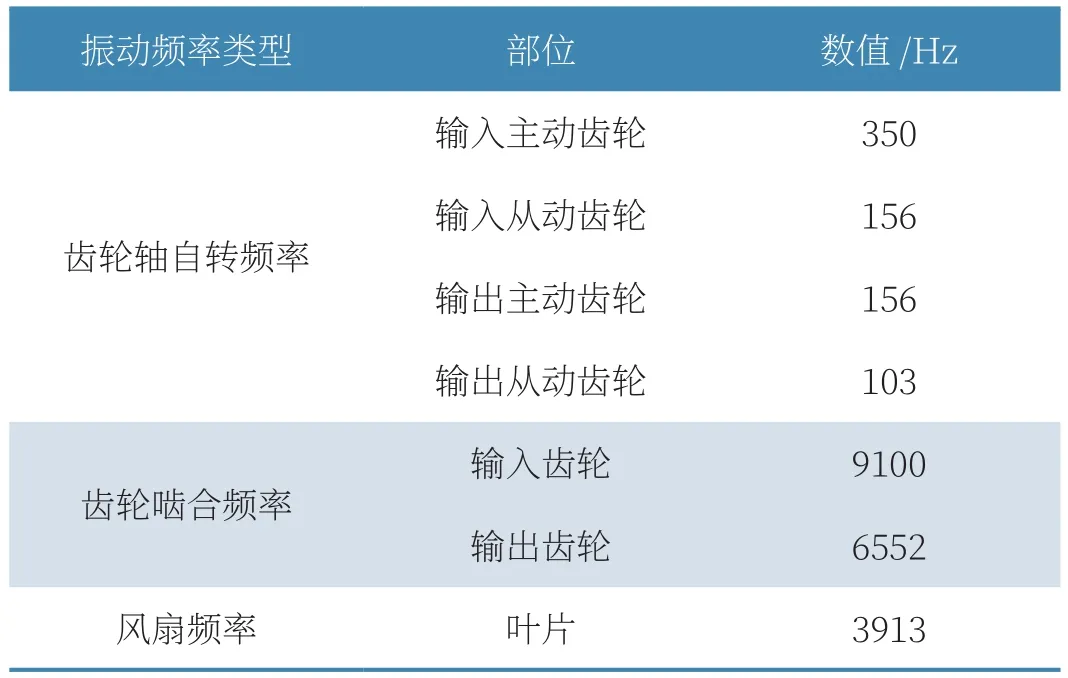
表1 振动特征频率

4.减速器噪声信号数值仿真

针对直升机减速器宽频噪声特性，选取输入主动齿轮轴自转频率350Hz、风扇叶片通过频率3913Hz、输出齿轮啮合频率6552Hz以及输入齿轮啮合频率9100Hz 4个主要振动特征频率，运用ESM法以及WBH法进行仿真。为探究不同阵列测量距离对宽频噪声的成像效果，设置阵列测量距离分别为0.1m、0.5m，将两个声源分别置于（-0.2,0）m与（0.2,0）m处，使用COMBO阵列进行仿真，图3为ESM法与WBH法对应4个频率点处的声源成像图。观察图3(a)，当阵列测量距离设置较近时，两种算法随着测量频率增加，其成像效果越差，主要表现为旁瓣增多，定位精度下降，当频率为9100Hz时，两种算法均无法完成双声源识别与定位任务，但WBH法在350Hz、3913Hz、6552Hz 3个频率点都能识别出两个声源的位置，而ESM法在6552Hz频率点处开始无法完成声源定位，该种方法使得左边声源点处产生了虚假声源点。再观察图3(b)，可发现WBH法在这4个频率点处都能准确识别出两个声源位置，且旁瓣较少，声音幅值计算也较精确，而ESM法仅能在3913Hz以及6552Hz处定位到两个声源位置。

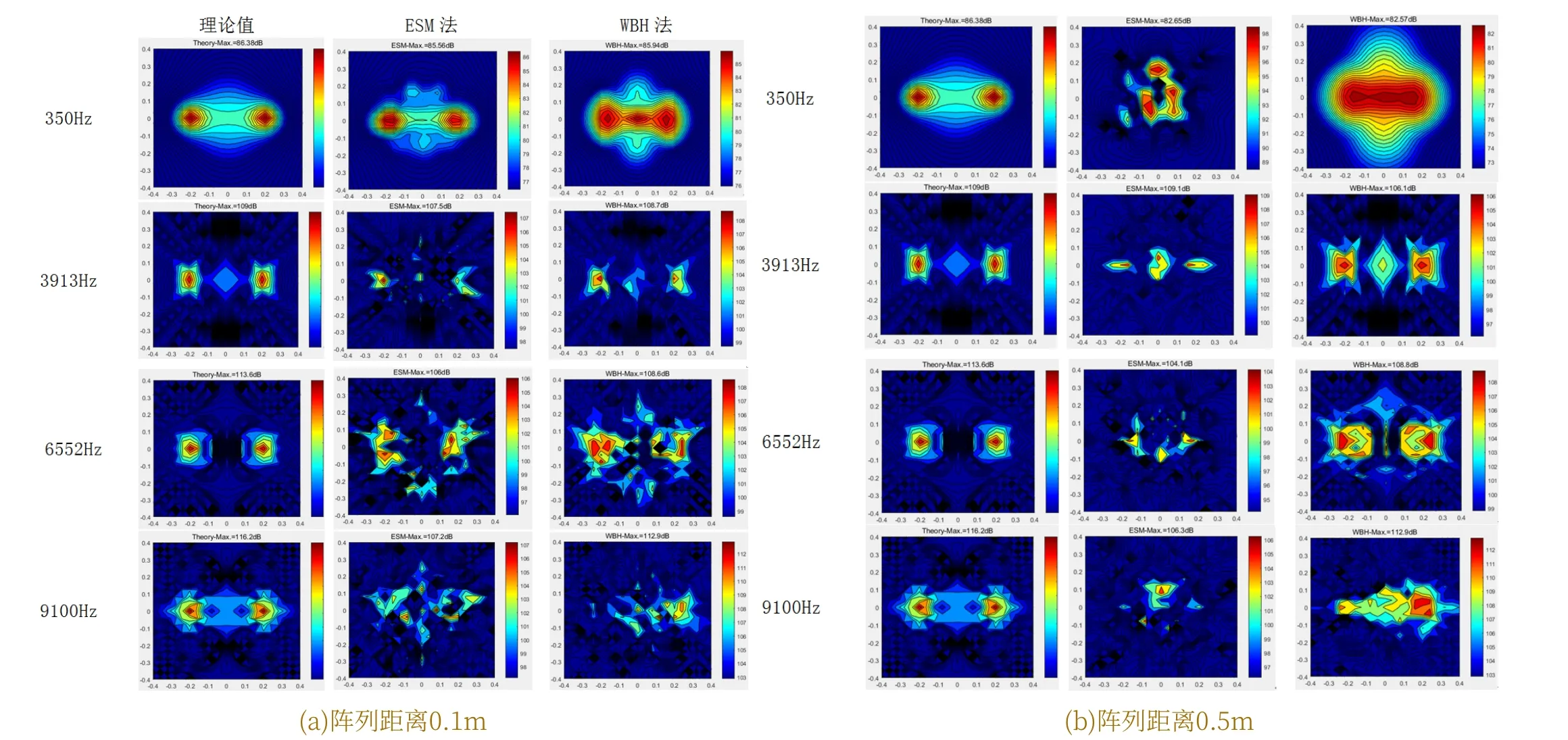
图3 ESM法与WBH法声源成像图

为进一步探究两种算法对宽频带噪声的声源定位精确度以及阵列测量距离对两种算法重建精度的影响，运用两种算法对频带100Hz～10000Hz的双声源声信号进行仿真，并设置阵列距离为0.1m～0.5m（间隔0.1m），定义重建误差为：

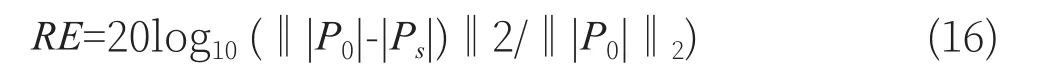
式中，RE代表相对误差，P0代表理论重建声压，Ps代表实际重建声压，RE的值越小，表示算法的重建误差越小，重建精度越高。得到两种算法在不同阵列测量距离下，对宽频噪声重建误差的对比曲线图，如图4所示。

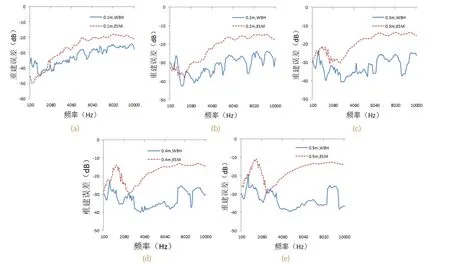
图4 不同测量距离下两种方法的重建误差曲线（SNR=40dB）

从图4中可以看到，虚线代表ESM法的重建误差，实线代表WBH法的重建误差，ESM法在阵列距离为0.1m，测量频段为100Hz～2000Hz的重建误差小于WBH法的，在阵列距离为0.2m，测量频段为100Hz～1000Hz间的重建误差小于WBH法的，其他部分WBH法的重建误差均小于ESM法的，这表明运用WBH法进行宽频噪声声源识别与定位较ESM法有更高的重建精度，由此，在本文中选取WBH法对某型直升机右头部减速器特征噪声频率进行试验验证，以证明该种算法对宽频噪声的适用性。

5.试验验证

5.1 试验条件

为验证WBH法对宽频噪声源定位的准确性及优越性，且为契合直升机减速器的试验条件，在封闭房间内进行试验。取某型直升机右头部减速器中输入主动齿轮轴自转频率350Hz、风扇叶片通过频率3913Hz、输出齿轮啮合频率6552Hz以及输入齿轮啮合频率9100Hz 4个主要振动特征频率，运用WBH法进行试验验证，设置阵列测量距离为0.5m。传声器阵列含有36个声传感器，采用COMBO阵列布局，如图5所示。

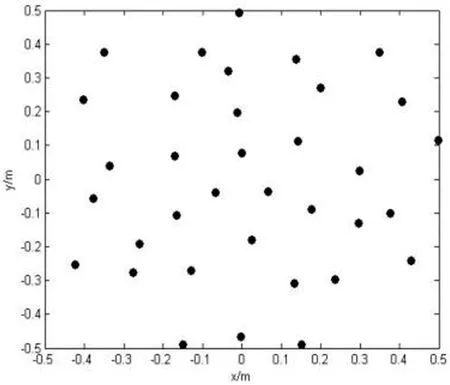
图5 传声器阵列布局

如图6所示为试验现场布置情况，将两个音响作为声源，与信号发生器相连接发出指定频率声音，两个音响间隔0.4m，位置坐标为（-0.2,0）m和（0.2,0）m。

图6 试验现场布置示意图

5.2 减速器特征频率试验验证

如图7所示，针对某型直升机右头部减速器中的这4个振动特征频率，无论是低频或是高频， WBH法都能准确识别出两个声源的位置，且旁瓣污染较少，无虚假声源出现。此外，从图7(d)中可以看出，WBH法的定位效果对高频声源都十分优越，随着测量频率的增加，WBH法成像结果中的声源主瓣宽度变窄，声源成像精度较高。试验结果表明，WBH法能够对宽频带噪声源准确定位，并能有效抑制旁瓣，提高聚焦性能。

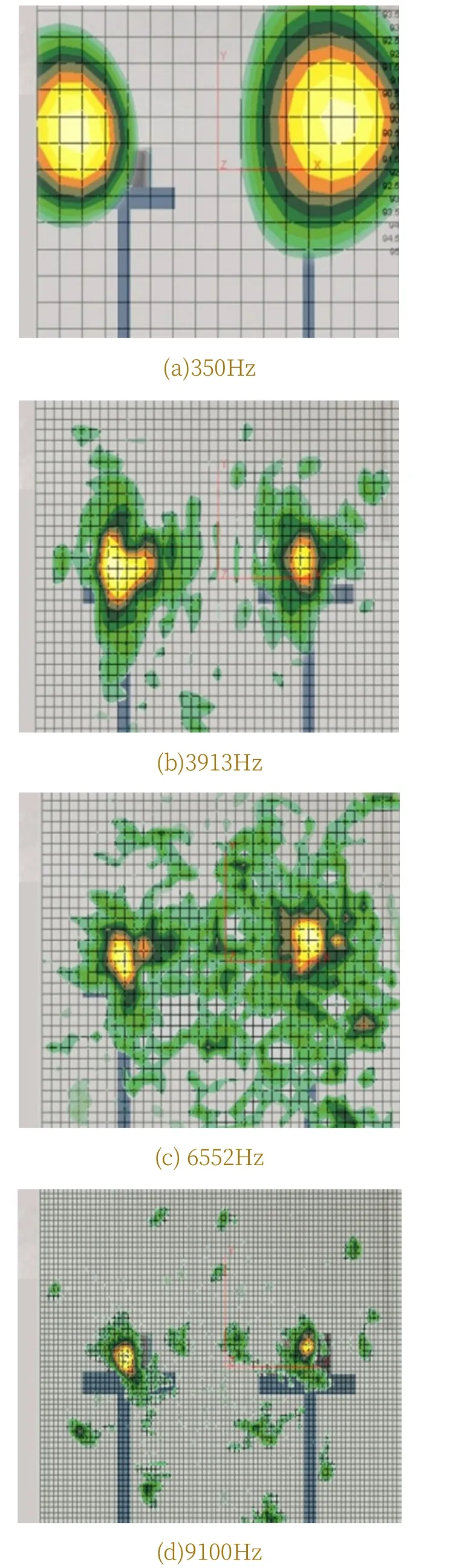
图7 阵列距离0.5m，WBH法双声源成像示意图

6. 结语

数值仿真结果以及试验验证结果都表明，WBH法能够实现对宽频噪声进行准确地声源定位，并能有效抑制声源旁瓣，缩小主瓣宽度，提高声源识别聚焦性能，针对宽频带噪声特征声源，该种方法能够实现准确定位。