车路协同下基于间隙理论的交叉口智能控制策略 *
潘福全,张 游,张丽霞,杨金顺,杨晓霞
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
0 引 言
自交通指挥信号灯设计出现以来,世界上道路交叉口普遍用该种信号灯来对交通流进行管控,“红灯停,绿灯行”的交叉口通行观念也早已深入人心。随着车路协同与智能驾驶技术的出现,传统的交通控制方式已不再适应智能交通时代的发展。信号灯控制系统在常年应用过程中也逐渐暴露出一些问题与弊端,主要体现在以下两个方面。
1)信号配时固定化。目前我国大多数信号灯控制系统运行方案都是按照一定规律进行运作的,当道路车流量突增时,现有信号灯控制模式不能及时有效地调配车流,无法适应实际通行需求,且存在部分车道在绿灯时间无车通行,出现“多等少”或空道占时现象,造成不必要的出行延误[1]。
2)易受外界因素影响。当遇大雾、暴雨等恶劣天气或后方小型车辆遇到前方大型车辆遮挡视野等时,信号灯系统无法向待行车辆及时准确地传达信息指令。
随着大数据、云计算、5G、人工智能等前沿技术向各个行业不断渗透,交通领域也迎来了全面深化变革,这些技术将有力推动智慧交通实现数字化、网联化、智能化的升级[2]。在智能交通基础设施布局建设完备条件下,车路协同技术将使道路上的车辆与周围环境紧密融合,通过运用一系列车载传感器等先进的电子设备实时感知道路状态,并将有效信息传递给ITS(intelligent transportation system)控制中心和车载控制单元,从而实现车与车、车与路、车与人、车与云的实时信息交互,为驾驶出行提供更加便捷、高效、安全的服务[3]。在这样一种高度智能化的交通生态体系中[4],对出行者困扰已久的交通拥堵问题势必会得到一定缓解。而道路交叉口作为最容易产生延误与拥堵的地点,其控制系统的变革也势在必行。
间隙理论基本思想是通过预先调整跟驰车辆之间的行车间距,使得冲突方向车辆能从该间隙中安全穿过,从而实现不停车通过交叉口的目的[5]。目前,国内外相关学者基于该理论对车路协同环境下的交叉口控制方法进行了大量研究。ZHANG Yi等[6]设计了一种车联网环境下基于交通信号和路况状态的行车速度引导方法,并开发了单车速度引导模型和多车协同速度引导模型,以减少交叉口处的行车延误与停车次数,提高交通控制效率;鹿应荣等[7]提出了一种车联网环境下不改变交叉口原有信号配时的车速控制策略,实现车辆高效平滑地通过道路交叉口,并在双向两车道的十字交叉口进行了模拟仿真,结果表明该速度控制策略能有效降低车辆通过路口的平均行程时间;刘欢等[8]对车路协同环境下网联车辆通过交叉口时匀速、加速、减速、跟驰这4种情况分别进行了分析,提出了不停车辆通过交叉口的速度引导数学模型,并基于VISSIM进行了仿真验证,结果表明该速度引导策略可大幅降低车辆延误时间,能够提高交叉口通行效率;R.TACHET等[9]提出的基于间隙控制的交叉口管理系统SIs(slot-based intersections)作为未来城市的智能交通基础设施,并在构建的框架内将其与交通灯系统控制性能进行对比,结果表明SIs系统能实现交叉口通行能力翻倍,可显著降低延误;M.AMIRGHOLY等[10]提出一种自主通信车辆协同控制策略,使交叉口处各向车队间的车头时距能满足交叉方向上的车队安全穿行,并构建了智能交叉口交通优化控制随机分析模型,验证表明该策略能够使交叉口通行能力提高138%;柴琳果等[11]在SIs间隙控制方法的基础上进行了改进优化,利用LOOSE(location optimization on sequence evaluation)和COMPACT(cooperative optimization method for previous allocation comparatively transforming)算法对即将进入交叉口的车辆状态进行计算分析,并做出对应的车辆控制决策,从而使交通流在无需减速停车的情况下能安全通过交叉口,该方法不仅能提高通行效率,而且适用性更加广泛;常玉林等[12]在车联网环境下,提出了基于间隙优化的无信号交叉口控制方法,以次路车能顺利穿越车流量较大的主路为目标构建了相应的控制模型,并验证该方法可提高交叉口通行效率,减少主路车流延误时间。
上述基于间隙理论的交叉口控制研究多是解决车辆的通行时间冲突,对交叉口内部的冲突点分析较为缺乏。笔者以典型十字型交叉口作为研究对象,基于间隙理论对交叉口冲突消解问题进行深入分析,提出一种车路协同环境下的交叉口智能控制策略,旨在使交叉口各方向车辆可依次交替穿插通过各冲突点,实现不停车通过交叉口,减少由交通控制装置所引起的固定延误,提高通行效率。
1 问题描述
传统信号灯交叉口控制系统是通过“断面式”的时间分离,使相互冲突的交通流在不同时间区段分批次通过交叉口,这种控制方法在一定程度上造成了通行时间浪费,增加车辆行车延误。实际上,交叉口车流冲突仅仅存在于局部的冲突点区域内,若采用一种“流体式”的时间分离方法,即冲突车流按照秩序依次交替穿插通过冲突点,不仅可保证行车安全,而且能大幅提升交叉口通行效率。
在车路协同环境下,交叉口远程控制中心可通过信息感知和智能决策对冲突车流进行协调管控。基于间隙理论的交叉口智能控制理念如图1。当主次路车辆进入交叉口控制区域时,各向车辆均提前调整当前行车状态,增大或缩小与前车之间距离以达到最优行车间隙Ui和U′j,从而满足主次路车辆在无碰撞条件下不停车通过交叉口的通行需求。
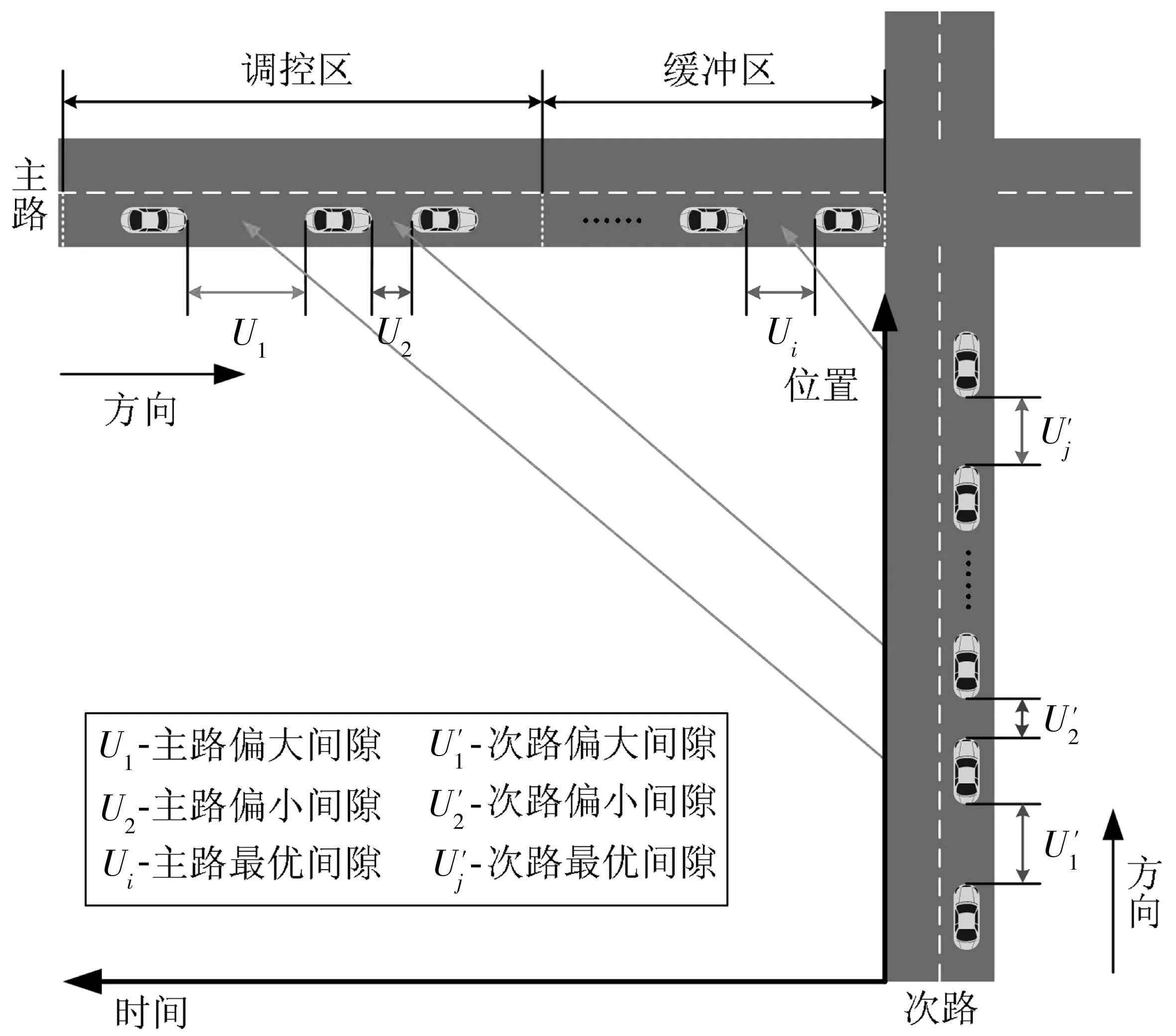
图1 问题描述宏观示意Fig. 1 Macro diagram of the problem description
基于该控制理念,主次路车辆在冲突点区域的通行演绎如图2。图2中:当主路Ⅰ号车完全驶离冲突点区域时,次路Ⅱ号车开始进入冲突点区域;当次路Ⅱ号车完全驶离冲突点区域时,主路Ⅲ号车开始进入冲突点区域,即主次路车辆交替穿插通过冲突点区域,实现交叉口冲突消解。
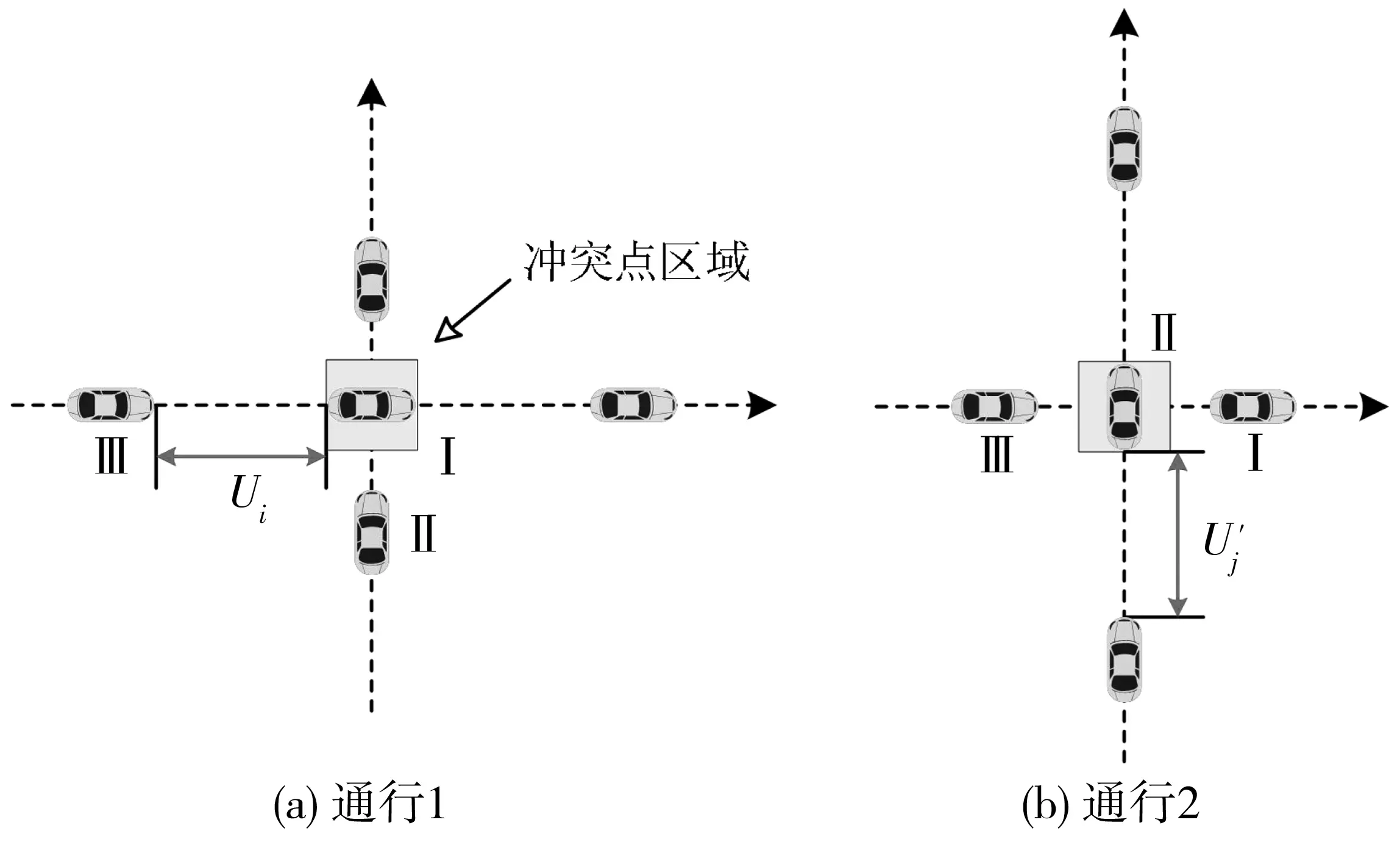
图2 问题描述微观示意Fig. 2 Microscopic diagram of the problem description
2 交叉口智能控制系统设计
2.1 前提假设
1)道路交通实现“聪明的车”和“智慧的路”,车载单元与路侧单元等基础硬件设施布局完备,数据信息传输速度与精准度、信号覆盖范围、抗干扰能力等满足要求。
2)交叉口控制中心具有强大的信息分析处理能力,能及时准确做出决策判断。
3)道路为机动车专用通道,不存在非机动车辆与行人等干扰问题。
4)交叉口通行的车辆类型为普通小型汽车,暂不考虑大中型客货运车、公交车等。
5)交叉口路段各功能区长度范围合适,车辆能在各功能区内完成相应的驾驶操作。
6)车辆在进入交叉口前后不允许进行合流与分流,即各向车辆均按照预设行车轨迹在相应的独立车道行驶。
7)车辆在交叉口通行过程中,均是沿各车道中心线行驶,且左转车辆交叉口内行车轨迹为1/4圆弧[13]。
2.2 路段功能区划分
按照该控制系统设计方案,道路交叉口附近不同距离路段被划分为不同功能区。车路协同环境下道路交叉口各路段的信号控制功能区与传统意义上的交叉口功能区不同,其存在意义是为了对进入或即将进入交叉口的车辆进行实时管控[14]。根据功能与用途不同,将交叉口附近各路段划分为变道区、调控区、缓冲区和穿行区这4个部分,如图3。在不同路段区域范围内,车载单元、路侧单元与交叉口控制中心各自执行相应的信息交互,实现智能化、精细化交通管控。
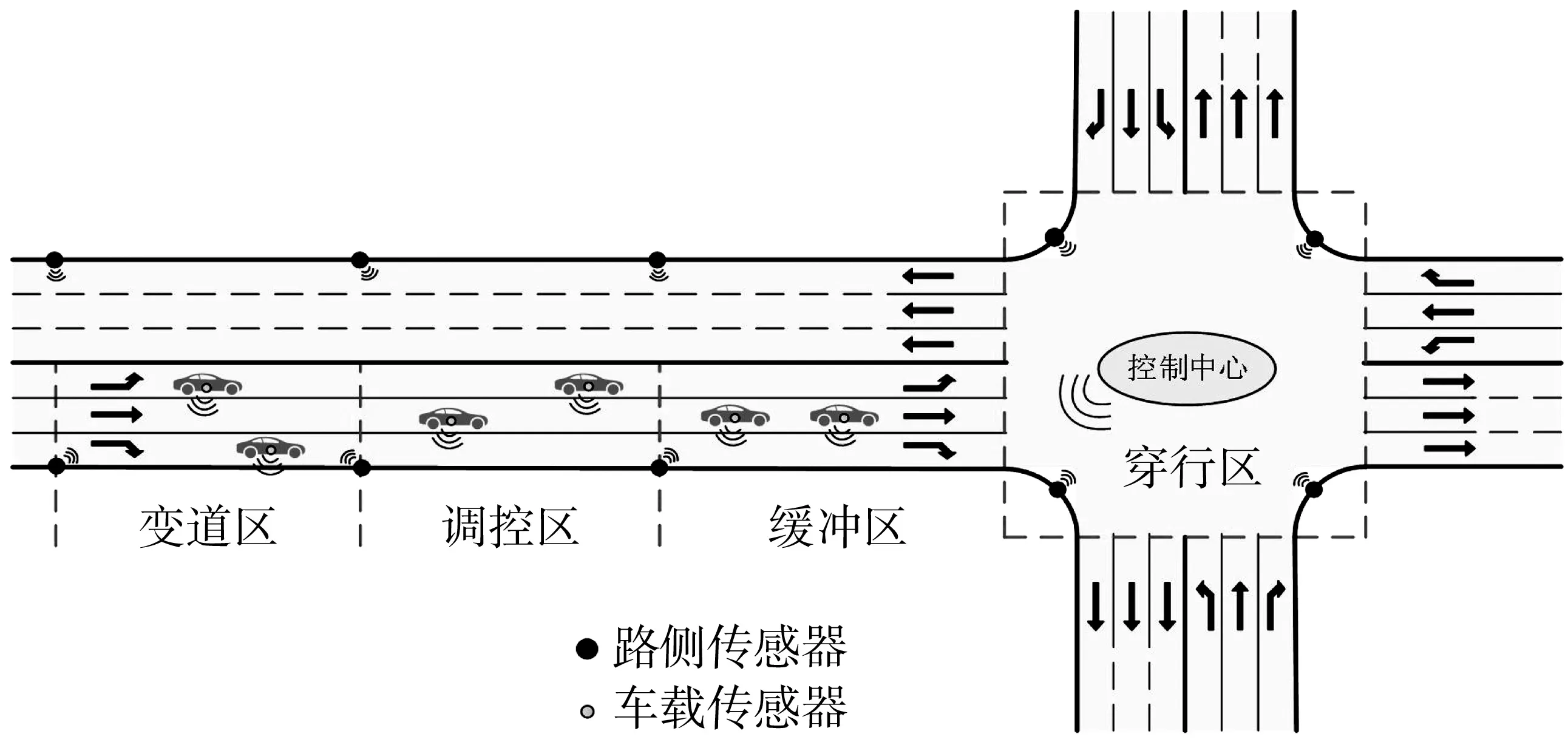
图3 车路协同环境下交叉口路段功能区Fig. 3 Functional area of intersection under vehicle-infrastructurecooperative environment
2.2.1 变道区
在此路段内各车辆按照行进方向提前变道至对应的导向车道;路侧传感器对本区各车道待通行车辆的行进信息进行实时监测,并将检测到的各车道交通相关数据发送至交叉口控制中心。
2.2.2 调控区
待通行车辆在此区段内接收来自交叉口控制中心发布的指令信号;车辆控制单元在接收到指令后调整当前行车速度,控制与前方车辆之间的行车间距至最优间隙,以满足相互冲突的车辆交替穿插通过交叉口冲突点的条件。
2.2.3 缓冲区
车辆进入缓冲区后均已达到控制中心指令要求的行车状态,并以当前状态匀速行进。
2.2.4 穿行区
车辆以允许的最优速度进入交叉口,按照控制中心指令实时调整行车状态,依次通过行驶路径上的各个冲突点,完成交替穿插通行。
2.3 控制策略
在车路协同环境下,道路上的行驶车辆通过车载传感器感知周边局部环境状况,获得道路上其他车辆的位置、驶向等信息,并通过自身车载单元向外界发送本车的各项运动信息[15]。路侧传感器可监测道路安全状况、路面湿滑状态等,同时接收局部区域内各个车载单元发送的动态信息,检测道路各车道的车流量、车道占有率、及车辆行车轨迹等道路信息[16]。基于上述两个模块采集到的交通数据信息,控制中心进行数据处理分析并做出决策判断。
当车辆驶入交叉口控制区域时,控制中心根据车辆预设行车轨迹,判断其在交叉口穿行区内是否存在交通冲突。若无冲突,位于调控区的车辆按照控制中心指令快速行进,在无冲突干扰条件下安全通过交叉口。若存在冲突,控制中心识别确认出冲突点位置,并计算各冲突点对应的最优行车间隙,车辆根据第一个冲突点最优行车间隙在调控区内调整当前行车状态,完成与前车之间的距离控制,并保持该状态驶入穿行区。车辆每通过一个冲突点,对行车间隙进行一次调整,直至通过穿行区内所有冲突点。图4为系统控制流程;图5为车辆调控过程。
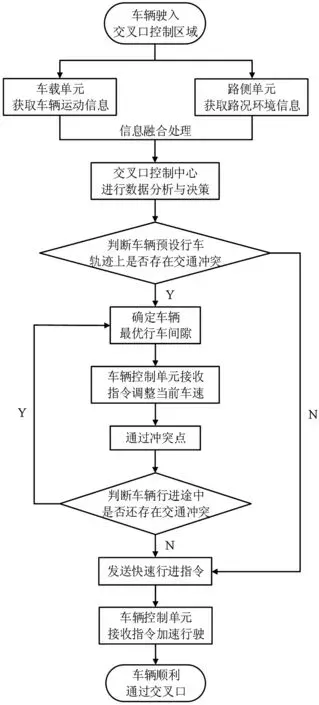
图4 系统控制流程Fig. 4 System control flow chart
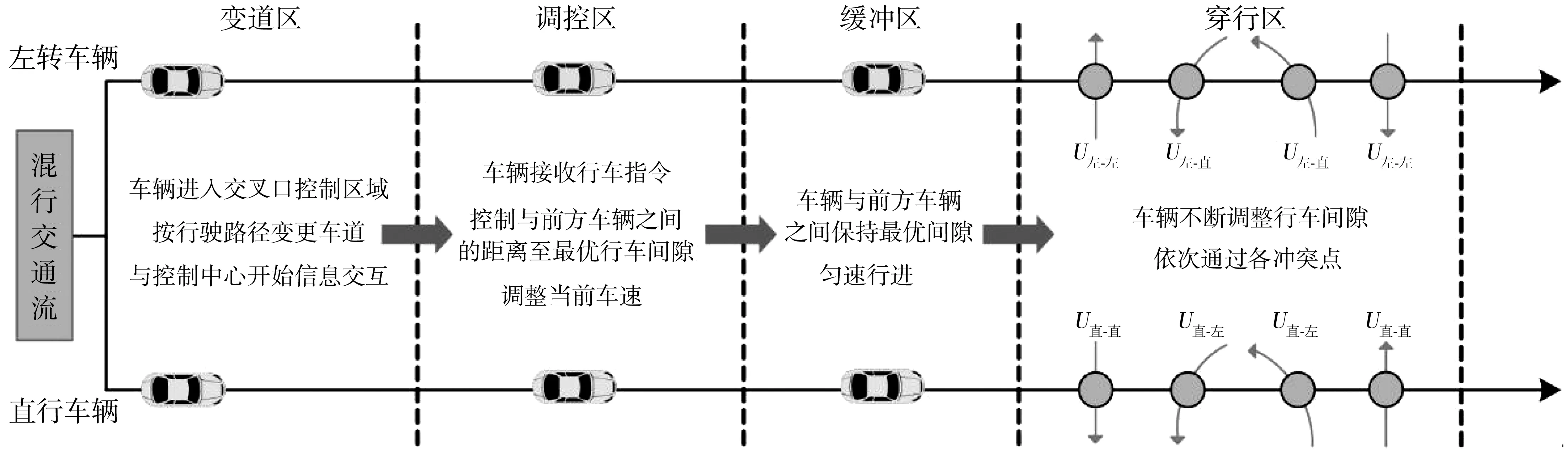
图5 车辆调控过程Fig. 5 Vehicle control process
3 控制模型
3.1 行车间隙控制模型
选取较为典型的双向六车道十字型交叉口进行分析。以交叉口中心点O为坐标轴原点建立直角坐标系,如图6。
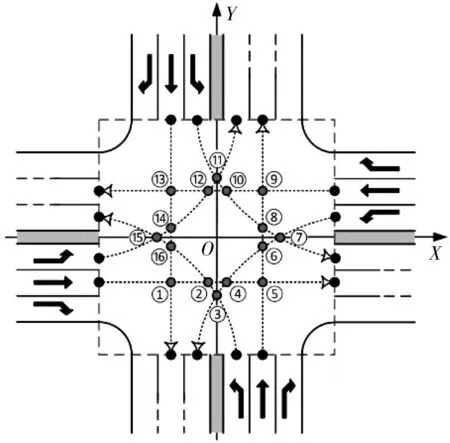
图6 双向六车道十字型交叉口冲突示意Fig. 6 Illustration of the conflict at two-way six-lane intersection
根据车辆行驶轨迹不同,可以把图6中的16个冲突点分为3类:
笔者分别以①、②、③为例,对直行和左转车辆经过3种类型冲突点处最优行车间隙进行分析。假设冲突点上的车辆通过顺序为第j辆车、第i辆车、第j+1辆车、第i+1辆车,如图7。
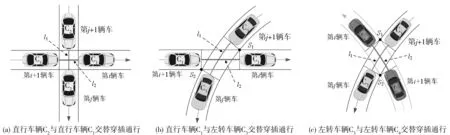
图7 冲突车辆交替穿插通行示意Fig. 7 Schematic diagram of alternately intenspersing traffic of conflicting vehicles
车辆交替穿插通过冲突点的次序为:当前一辆车完全驶离冲突点区域时,后车恰好开始进入冲突点区域。在车辆行驶过程中为保持行车间隙不变,同一驶向的车辆在通过冲突点前速度相同,即vj=vj+1,vi=vi+1。
行车间隙控制模型目标函数为车辆交替穿插通过冲突点时的安全行车间隙最小,其表达如式(1)、式(2):
(1)
(2)
式中:Ui-(j+1)为第i辆车通过冲突点时,第j+1辆车和前车(即第j辆车)之间的行车间隙,m;U(j+1)-(i+1)为第j+1辆车穿插通过冲突点时,第i+1辆车和前车(即第i辆车)之间的行车间隙,m;vi为第i辆车通过冲突点时的行驶速度,m/s;l1为冲突点区域对j方向车辆的作用距离,m;l2为冲突点区域对i方向车辆的作用距离,m;s为车辆长度,s=5 m。
行车间隙控制模型的约束条件如式(3)~式(5):
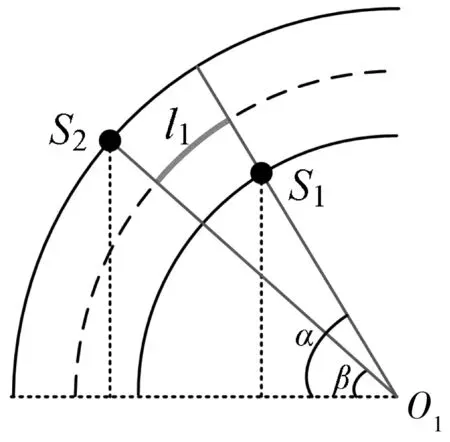
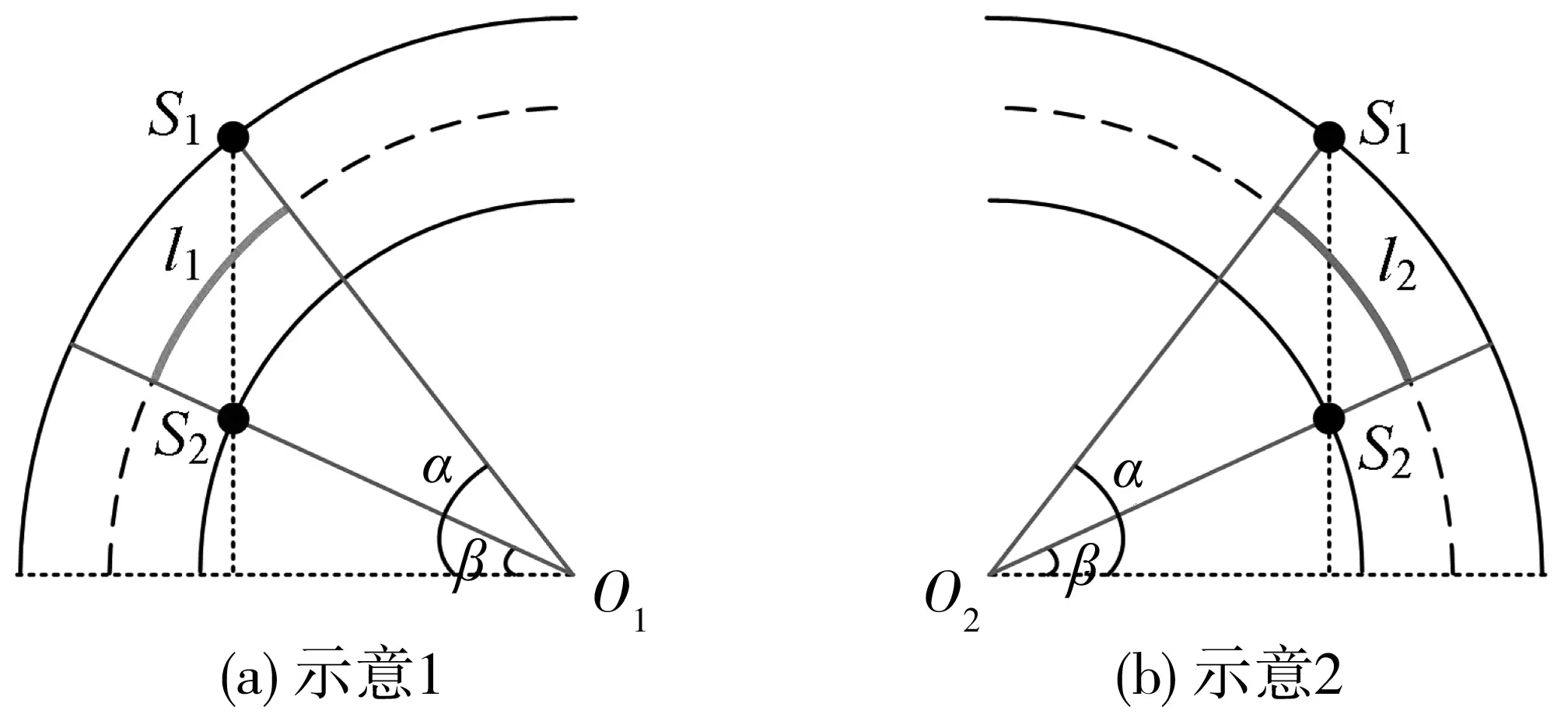
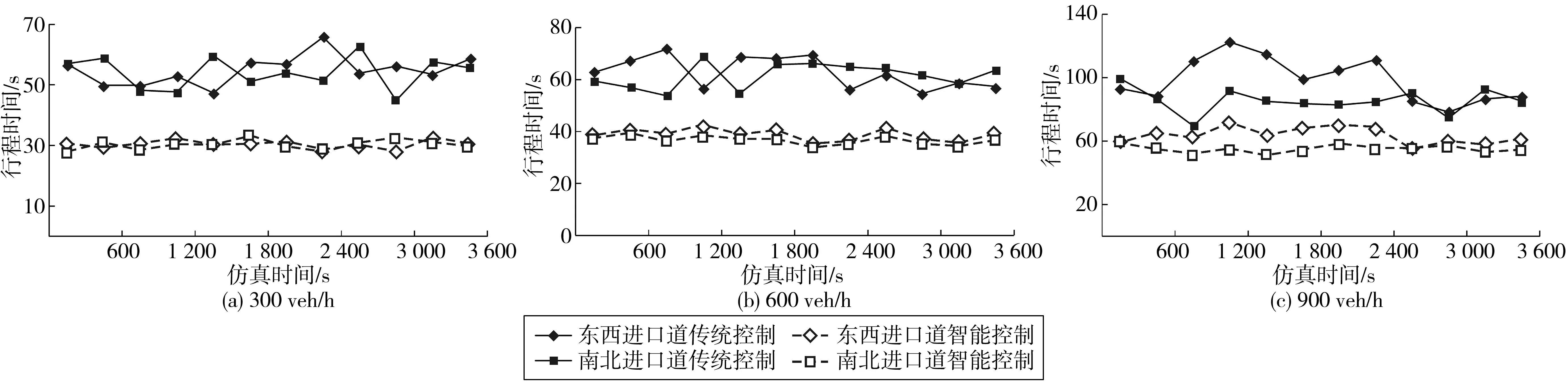
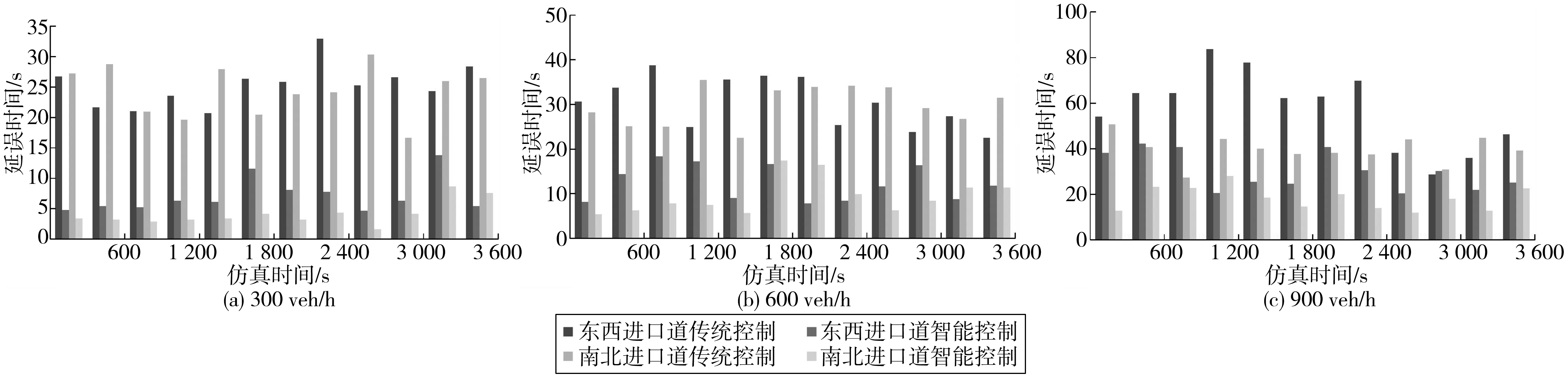
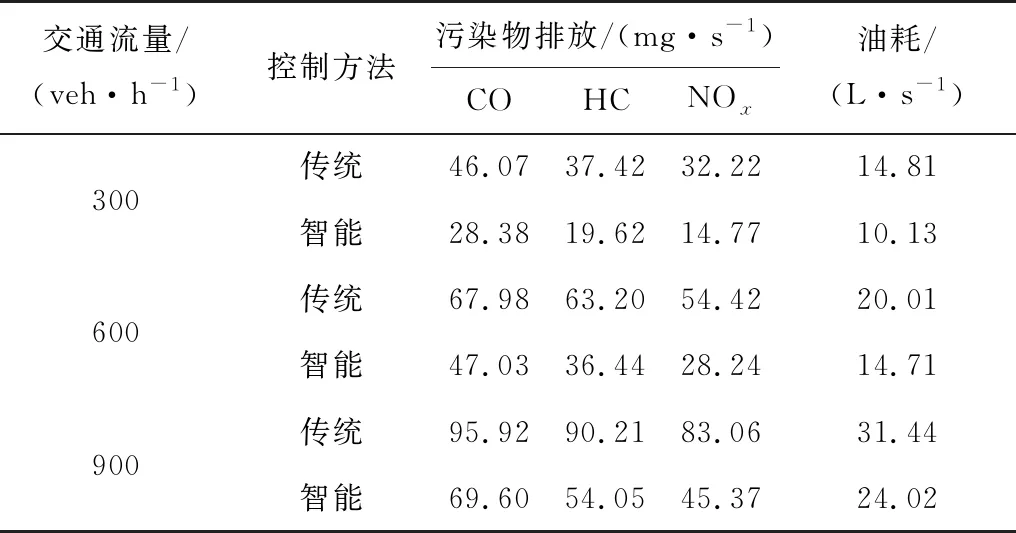
0≤v直 (3) 0≤v左 (4) (5) 式中:v直、v左分别为直行和左转车辆在交叉口控制区域内的行驶速度,m/s;v限为交叉口路段车辆最高限速,m/s;k为道路状况、车辆技术状况及环境因素等影响车辆安全行驶的综合系数;g为重力加速度,m/s2;μmax为道路路面的最大静摩擦系数;r为左转车辆的转弯半径,m。 3.1.1 直行与直行冲突点 冲突点处的车辆通行示意如图7(a),则有式(6): l1=l2=w+2d (6) 式中:w为车辆宽度,m;d为车辆侧向净空宽度,m。 3.1.2 直行与左转冲突点 冲突点处的车辆通行示意见图7(b)。结合图6所建坐标系可得碰撞点S1、S2坐标: 冲突区域作用距离微观示意如图8。通过几何计算可得式(7)~式(10): (7) (8) (9) (10) 式中:l为道路车道的宽度,m;α和β分别为转弯车辆冲突区边界点与转弯圆心的夹角,(°)。 图8 冲突区域作用距离微观示意Fig. 8 Microscopic diagram of conflict zone action distance 3.1.3 左转与左转冲突点 冲突点处的车辆通行示意见图7(c)。结合图6所建坐标系可求得碰撞点S1、S2坐标: 冲突区域作用距离微观示意如图9。通过几何计算可得式(11)~式(13): (11) (12) (13) 通过冲突区域作用距离分析,可得式(14)~(19): (14) (15) (16) (17) (18) (19) 式中:UW直-N直、UN直-W直分别为X、Y方向直行车辆交替穿插通过冲突点时的最优行车间隙,m;UW直-E左、UE左-W直分别为X、Y方向直行和左转车辆交替穿插通过冲突点时的最优行车间隙,m;US左-E左、UE左-S左分别为X、Y方向左转车辆交替穿插通过冲突点时的最优行车间隙,m;vN直、vW直、vE左、vS左分别为Z方向上直行或左转车辆通过冲突点时的行驶速度,m/s。 图9 冲突区域作用距离微观示意Fig. 9 Microscopic diagram of conflict zone action distance 交叉口控制中心根据预先感知的车辆行驶状态信息分析预测交叉口车流冲突,运用行车间隙控制模型实时进行车辆通行间隙运算,并通过车辆状态动态调整的方式使车辆之间达到最优行车间隙,从而实现交叉口的智能控制。 3.2.1 调控区内的车辆状态调整 车流在经过交叉口时一般具有明显的车队特征[17],即相冲突的两路车流均是以车队形式交替穿插通过冲突点的。当某进口道有一股车流W进入到交叉口控制区域时,控制中心将其分为若干个连续的子车队W1,W2,…,Wm,并以子车队为单位进行车辆状态调整。其中:每个子车队中所有车辆在交叉口穿行区内遇到的冲突状况相同。 如Wk子车队中包含n辆车,当车队中车辆进入到交叉口调控区路段后,需将车辆从当前的行驶状态A调整至目标状态B,使车辆与前车之间形成最优行车间隙。目标状态包括车辆位置、速度、加速度、调整时间和与前车的行车间隙,调整过程如下: 其中:xai、vai、aai、tai、uai分别为子车队第i(i=1,2,…,m)辆车在交叉口调控区的初始位置、行驶速度、设定加速度、进入调控区时间、与前车的行车间隙;xbi、vb、ub分别为车辆目标状态下在交叉口调控区的位置、目标速度、目标最优行车间隙;tbi为完成状态调整后的时间。 在目标状态下属于同一子车队中的车辆均保持相同最优行车间隙匀速行进,故加速度为0。视车辆在本阶段状态调整中做匀加/减速行驶,则车辆状态调整时间Δti如式(20): (20) 因车辆需要在交叉口调控区长度范围内完成状态调整,故状态调整时间的约束条件如式(21): (21) 式中:l调控为交叉口调控区长度,m。 3.2.2 穿行区内的车辆状态调整 当Wk子车队中车辆在调控区内完成状态调整,并保持一定状态通过穿行区内的第一个冲突点后,由于后续冲突点上车辆行驶状况有所改变,故需对子车队中车辆的行驶状态继续进行微调,调整过程如下: 其中:B为上一阶段的目标状态,亦为本阶段车辆行驶的初始状态;C为车辆调整的过程状态;D为车辆调整的目标状态。vd、ub分别为本阶段状态调整时的初始速度和初始行车间隙;vci、aci、uci分别为第i辆车状态调整过程中的速度、加速度和行车间隙;vd为状态调整的目标速度;ud为状态调整的目标行车间隙,即车辆通过下一个冲突点时与前车之间最优行车间隙。 视车辆在本阶段状态调整中同样做匀加/减速行驶,则车辆状态调整时间Δt′i如式(22): (22) 式中:v0为车辆的初始速度。 此阶段车辆需在到达下一个冲突点前完成状态调整,故状态调整时间约束条件如式(23): (23) 式中:l冲-冲为车辆行驶路径上两冲突点之间距离。 在Vissim仿真环境中构建双向六车道十字交叉口,通过MATLAB调用COM接口[18-19],将笔者提出的控制方法与传统信号灯控制进行对比分析。信号灯控制方法采用二相位定时信号控制,周期时间T=100 s,其中各相位绿灯时长45 s,绿灯间隔5 s,车辆跟驰最小安全距离设为5 m。车路协环境下的交叉口路段控制区域范围设定为700 m,其中变道区长度为100 m,调控区为400 m,缓冲区为200 m。交叉口各方向进口道均为1左转、1直行和1右转,每条车道宽为3.5 m,左转车辆转弯半径为15.75 m。道路最高限速60 km/h,最低限速10 km/h。仿真预热时间600 s,仿真时长3 600 s。 仿真中设定东西进口道左转、直行、右转交通流量分配比例为3∶5∶2,南北进口道左转、直行、右转交通流量分配比例为4∶3∶3,分别对不同交通流量下两种方法的控制效果进行仿真评价。 4.1.1 车辆行程时间 图10为不同交通流量下东西进口道和南北进口道车辆行程时间对比结果。当交通流量分别为300、600、900 veh/h时,东西进口道车辆行程时间分别缩短44.47%、38.19%、35.07%,南北进口道车辆行程时间分别缩短44.15%、40.53%、35.57%。由于智能控制下交叉口车辆无需怠速停车,故通过交叉口行程时间得到显著缩短;车辆一直处于行驶状态,故智能控制下车辆行程时间波动也较小。 4.1.2 车辆延误时间 东西进口道和南北进口道车辆平均延误时间对比结果见图11。当交通流量为300 veh/h时,传统控制下的车辆在一个信号灯周期内即可通过交叉口,此时车辆平均延误时间较短。随着交通流量增加,传统控制下交叉口排队车辆增多,造成更多停车延误同时,使得车辆排队等候时间也越来越长。在智能控制下,车辆是在行进中通过车速动态调整来避免交通冲突,当交通流量较大时,车辆通行速度减慢,故延误时间有所增长。由于智能控制下车辆无需进行频繁的启停行为,因此车辆延误较传统控制能大幅降低。当交通流量分别为300、600、900 veh/h时,东西进口道车辆平均延误时间分别降低71.82%、59.37%、47.57%,南北进口道车辆平均延误时间分别降低82.95%、68.23%、53.85%。 图10 不同交通流量下车辆行程时间对比Fig. 10 Comparison of vehicle travel time under different traffic flows 图11 不同交通流量下车辆平均延误时间对比Fig. 11 Comparison of average vehicle delay under different traffic flows 运用VT-Micro模型(virginal tech microscopic emission model)[20]对两种控制方法下的车辆主要污染物排放与油耗情况进行对比,仿真评价得出的相关数据如表1。 表1 不同控制方法下车辆污染物排放与油耗对比Table 1 Comparison of vehicle pollutant emission and fuelconsumption with different control methods 由表1结果可看出:交叉口智能控制下车辆污染物排放与油耗均得到有效减少。例如在低车流密度(300 veh/h)环境下,智能控制交叉口车辆通过调整最优行车间隙,能以稳定的车速快速通过交叉口,因此经济与环境效益提升较大,CO、HC和NOx排放分别减少了38.4%,47.6%,54.2%,车辆油耗降低了31.6%。随着车流密度增大,为保持最优行车间隙,智能控制下交叉口车辆需以较低车速行驶,故效益提升幅度稍有降低。 笔者提出了一种车路协同环境下的交叉口智能控制策略,对交叉口路段功能区进行了定义划分,在综合考虑效率与安全前提下,设计了基于间隙理论的交叉口智能协调控制工作流程,建立了交叉口冲突区域范围计算模型,并由此提出车辆行车间隙控制与车辆状态调整模型。仿真结果表明:该智能控制方法能使车路协同环境下的车辆不停车安全通过交叉口,所建模型合理有效,不仅可提高车辆在交叉口区域的通行效率,且能有效降低油耗与污染物排放。 需要注意的是,所提出的控制策略是基于较为理想的交通环境下展开,交叉口智能控制的实现还将依赖于车联网与智能驾驶技术发展,以及未来智能交通基础设施的布局建设。由于交叉口区域的环境复杂性与多变性,在后续工作中还需进一步开展深入研究。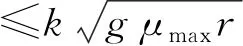
3.2 车辆状态调整
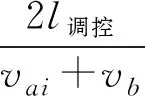
4 仿真分析
4.1 车辆通行效率对比分析
4.2 经济与环境效益对比分析
5 结 语

