基于蚁群算法与遗传算法的TSP路径规划仿真

圣文顺，徐爱萍，徐刘晶

(1. 南京工业大学浦江学院，江苏 南京 211200；2. 武汉大学计算机学院，湖北 武汉 430072)

1 引言

蚁群算法和遗传算法都是通过模拟自然界某种生物现象而得到的一种进化算法，它们在组合优化、规划策略等领域都表现出了各自的优越性。蚁群算法利用正反馈机制[1]，能较快地向较优解收敛，但易出现早熟、停滞现象；而遗传算法具有较强的全局搜索能力，可避免陷入局部最优。本文通过两种算法的结合，发挥各自优势，在加速收敛的同时有效地避免了陷入局部最优。另外通过引入贪心策略[2]，极大地提高了搜索速度，并在一定程度上解决了蚂蚁算法在搜索初期由于信息素缺乏进化缓慢的问题。实验表明，在求解旅行商问题时，与传统的蚁群算法和遗传算法相比，本文算法优势较为明显。

2 蚁群算法及遗传算法

2.1 蚁群算法

蚁群算法(ACA)是由意大利学者M.Dorigo提出的一种新型模拟进化算法[3]。实验观察表明，蚂蚁在其经过的路径上会留下一种挥发性分泌物(即信息素[4]，pheiomcme)，后续的蚂蚁会根据信息素的强度自主选择要经过的路径，通常的策略就是蚂蚁会选择信息素强度较大的路径行走。蚁群的这种集体行为可以理解为一种信息的正反馈机制的形成，蚂蚁通过该机制来定位通向目的地的最短路径，如图1所示。

图1 蚁群算法示意图

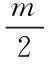
(1)

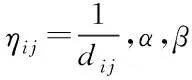
τij(t+1)=(1-ρ)τij(t)+Δτij

(2)

其中ρ∈(0，1)，表示信息量的衰减程度。信息量增量Δτij可表示为：

(3)

(4)

其中，Q是常数，Lk为蚂蚁k在本次循环中所走路径的总长度。

2.2 遗传算法

遗传算法(Genetic Algorithm，简称GA)最早于1975年由美国Michigan大学的J.Holland首先提出[6]，该算法基于达尔文的进化论，模拟了自然选择、物竞天择和适者生存，通过N代的遗传、变异、交叉、复制，进化出问题的最优解，是模拟生物遗传选择和优胜劣汰进化过程的一个计算模型。

遗传算法的处理流程是将所求问题的每个可能解都看作是一个染色体个体，将可能解个体进行特定编码，多个可能解个体即构成了一个群体。初始情况下，一般是随机产生一个群体，根据初始群体中每个个体的适应度利用遗传算子进行选择(Selection)、交叉(Crossover)和变异(Mutation)操作，对它们进行重新组合，进而得到一个新的群体。新的群体由于继承了上一代的优良特性，产生了一些向好的变化，从而逐步向着更优解的方向进化。

遗传算法具有与领域无关的群体性全局搜索能力，并且它的过程简单，可扩展性强，易于与其它优化技术结合。

3 蚁群算法与遗传算法的融合

蚁群算法主要利用信息正反馈原理强化较优解，当进化到一定代数后蚂蚁将聚集于信息量高的部分路径上，易出现早熟、停滞现象，陷入局部最优。为解决该问题，本文利用遗传算法具有随机选择性高、全局搜索能力强的特点，在蚁群算法进化到一定代数后，动态过渡到遗传算法，从而有效避免陷入局部最优的困境。具体方法是这样的：设定蚁群算法最小进化率Antmin-ratio，如果连续Antmax代没有得到更优解或者更优解的进化率都小于Antmax-ratio，说明蚁群算法很可能已陷入局部最优，这时就自动过渡到遗传算法。遗传算法的初始群体在蚁群算法运行过程中动态生成，建立一个N×n的二维数组C，N为群体规模，n为染色体长度(城市个数)，每巡游完一次就对每只蚂蚁所经路径的长度进行计算，找出本轮最小值，并与数组C中的每个染色体所对应的路径长度相比较，如果这个最小值小于某个染色体所对应路径的长度，则用这个最小值对应的路径替换掉该染色体。

本文把融合了这两种算法的算法称为ACAG算法(the Algorithm Combined by ACA and GA)，图2为ACAG算法简要流程图。

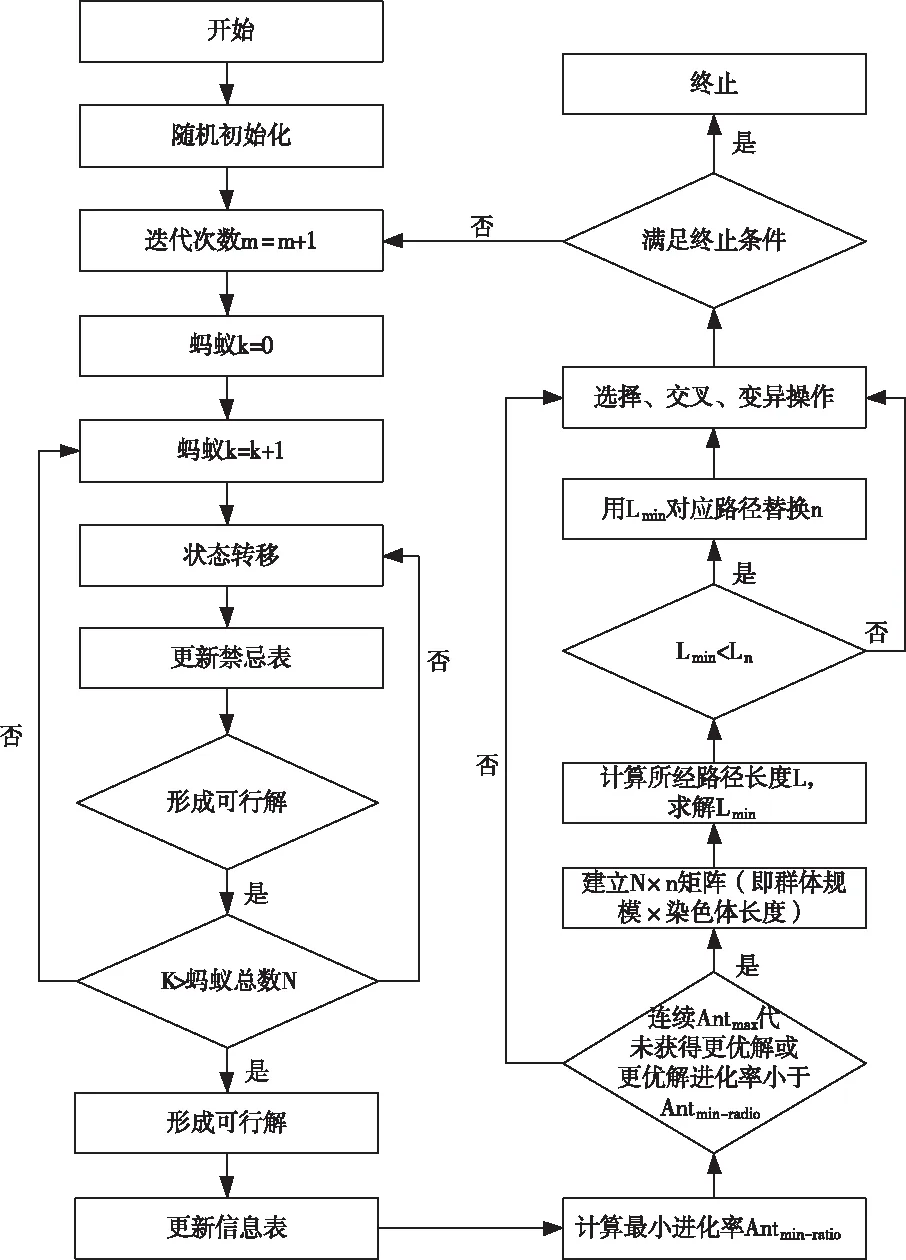
图2 ACAG算法流程图

4 基于ACAG求解TSP问题

4.1 ACAG中的蚁群算法规则

1)贪心策略

根据文献[7]，在一条遍历所有城市的较优路径中，城市i连接到城市j，j不可能是离城市i最远的那些城市。所以，把下一个城市的选择范围限定在离当前城市最近的w个城市中，只需对这部分城市的转移概率计算即可。在选择下一城市时，先找到离当前城市最近的w个城市，然后在这w个城市中找出蚂蚁本轮还未曾走过的h个城市。在h个城市中，按式(5)选择下一城市j。

(5)

贪心策略的采用，由于把可选择城市限定在一定范围内，使得搜索速度大大提高，并同时解决了蚂蚁算法搜索初期由于信息素缺乏进化缓慢的问题。

2)信息素更新策略

由于采用了贪心策略，蚂蚁会集中在相对较优的几条路径上，如果按传统的信息素局部更新方法，这几条路径上的信息素会迅速增加，从而导致过早陷入局部最优。为尽量避免这种情况，这里采用如下方法进行局部更新。

(6)

其中，τ0表示每条边上所允许的信息量最大值，Q1、Q2是可以设定的常量，Q2取值一般要比Q1大，当某条路径上的信息量大于τ0时，就较大幅度地削减其信息量，从而使蚂蚁选择其它路径的概率增加。

当所有蚂蚁完成一次循环以后，要对信息量进行全局更新，这里只对每次循环M最优路径上的信息量进行更新以强化最优解。如下式

(7)

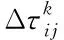
4.2 ACAG中的遗传算法规则

遗传编码：采用最自然的路径表达方式，如城市的编号为{1，2，3，4，5，6，7}，则某个染色体的编码位串可能为(3 2 5 1 4 7 6)，表示按顺序3-2-5-1-4-7-6来访问各城市。

适应函数：设路径总长度为f(n)，设置适应函数为1/f(n)，函数值越大表示路径越短，适应度越大，个体被选取的概率也就越大[9]。

交叉算子：采用由Davis提出的OX算子[10-11]。通过从一个亲体中挑选一个子序列并保存另一个亲体的城市相对次序来构造后代，例如两个亲体(两个“|”之间为挑选出的子序列)

p1=(1 2 3 | 4 5 6 7 | 8 9)=(4 5 2 | 1 8 7 6 | 9 3)

经过交叉操作后可得

变异算子：在染色体上随机地选择两点，然后对两点间的子串进行如下操作：从第一个城市开始，依次交换两个邻接城市的顺序，若能改善解则交换，否则不交换，直到子串的最后两个城市[12]。这样能提高遗传算法的局部搜索能力。

选择算子：采用遗传算法中应用最广的赌轮盘选择策略[13]。

4.3 ACAG求解TSP问题的算法过程

首先执行蚁群算法，并动态生成遗传算法所需的初始种群，直到达到转化条件为止，然后执行遗传算法直到结束。

1)蚁群算法部分

①初始化蚁群算法各参数，设置蚁群算法结束条件；

②反复执行下列操作，直到满足转化条件：

a. 将m只蚂蚁随机分布在n个城市中并设置到禁忌表中；

b. 对于每一只蚂蚁，按贪心策略选取下一城市j，选择完后将j加入禁忌表tabuk；

c. 当每一只蚂蚁走完一条边以后，按式(6)进行信息素局部更新；

d. 重复b.和c.，直到所有蚂蚁完成一次周游为止；

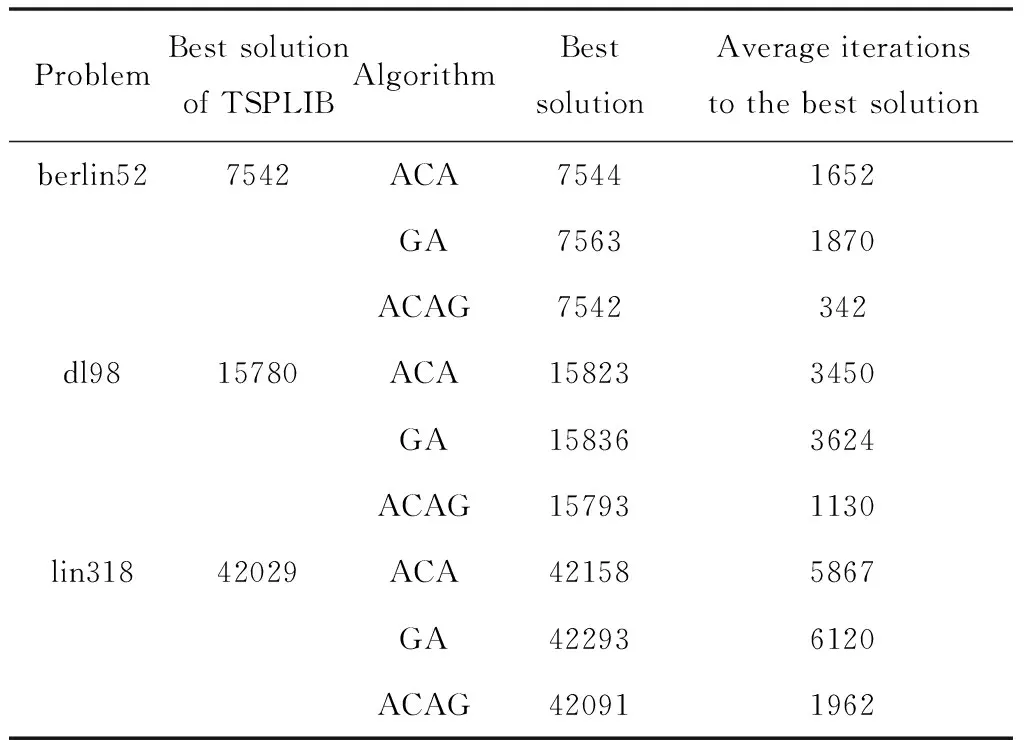
e. 当m只蚂蚁完成一次周游以后，计算每只蚂蚁所经过的路径长度，找到本轮最短路径lmin，并与已得到的最优长度lshortest相比较，若有lmin

f. 更新二维数组C；

g. 按式(7)进行信息素全局更新；

h. 清空并初始化禁忌表。

2)遗传算法部分

③设置杂交概率pc和变异概率pm，设置最大遗传代数[14]；

④初始群体P(0)(t=0)由二维数组C表示，群体规模为N；

⑤计算P(0)中每个个体的适应度；

⑥反复执行下列操作，直到达到最大遗传代数[15]：

a. 根据个体适应度计算每个个体被选择的概率pi；

b. for(k=0；k

{

根据每个个体的Pi及赌轮盘规则在P(t)中选择两个父体；

产生随机数rand∈(0，1)；

if(rand≤pc)，对两个父体进行交叉操作，将两个后代加入到新群体P(t+1)中；

}

c. 对P(t+1)中的每个个体按概率pm进行变异操作[16]；

d. 计算P(t+1)中每个个体的适应度，并更新最优长度lshortest和最优路径表；

e.f++；

⑦算法结束，输出最优长度和最优路径表。

按照以上算法步骤在MATLAB运行实验，所得结果如图3、图4。其中图3为城市中各点分布坐标，红色线段为起始坐标点(城市)的连线。图4为路径长度变化曲线，可获得最优长度及最优长度所对应的迭代次数。

图3 ACAG算法遍历旅行商问题优化结果

图4 ACAG算法中路径长度变化曲线及规律

5 实验结果及分析

利用Java程序分别实现了传统蚁群算法和遗传算法以及上述ACAG算法，并从TSPLIB实例库[17]下载了多个典型的TSP问题进行实验，都取得了比较好的结果。表1是三种算法的对比测试结果。表中第二列是指到目前为止对某个TSP问题已知的最优解，第四列表示各算法得到的最优解，最后一列表示达到最优解的平均迭代次数，ACA、GA和ACAG分别表示传统蚁群算法、传统遗传算法和本文算法。各个问题名称中的数字即所包含的城市数。

由表1可以看出，本文算法具有较强搜索最优解的能力，在berlin52、dl98、lin318三个典型的TSP问题中，采用本文算法得到的最优解与目前此TSP问题最优解最为接近，在berlin52问题中，两者数值相等。在蚁群算法阶段通过引入贪心策略大大加快了收敛速度，经较少的迭代次数能找到最优解。对问题lin318，传统蚁群算法和遗传算法分别需要5000多次和6000多次才能找到最优解，而本文算法仅需2000次左右。

表1 三种算法的对比结果

另外，图5、图6还给出了三种算法求解同一TSP问题的收敛特性比较。图中横坐标表示迭代次数，纵坐标表示路径长度，曲线1对应的是本文算法，曲线2对应的是蚁群算法，曲线3对应的是遗传算法。图5是eil51的收敛过程，图6是prl07的收敛过程。

图5 三种算法优化eil51的收敛特性比较

图6 三种算法优化pr107的收敛特性比较

由于对算法中各参数的确定并没有严格的理论指导，都是通过实验确定的，所以对不同TSP问题参数选取略有不同。如对eil51选取的参数如下：m=30，w=5，q0=0.8，β=3，ρ=0.15，Q=1000，Q1=1，Q2=5，Antmax=60，Antmin-ratio=1%，N=50，pc=0.8，pm=0.3。而对prl07选取的参数为：m=70，w=10，q0=0.8，β=3，ρ=0.1，Q=10000，Q1=10，Q2=100，Antmin-ratio=2%，N=50，pc=0.8，pm=0.15。

由图5、图6可以看出，传统蚁群算法和遗传算法的收敛性大致相当，而本文算法的优势很明显，经较少次数就能找到最优解。如图5中本文算法仅需10次就取得了437的值，而传统蚁群算法和遗传算法则需要几百次才能找到这样的值。

6 结语

本文对蚁群算法和遗传算法进行了有效结合，利用各自优势，在加速收敛的同时有效避免了陷入局部最优，并通过实验证明达到了预期效果。但该算法中的参数较多，不易控制，需经过反复实验寻找最优参数组合，在接下来的工作中需要对这些参数的选择作进一步的深入研究。