基于超像素分割与三维空间的图像哈希

刘 帅，赵 琰

(上海电力大学电子与信息工程学院，上海200120)

1 引言

科技的发展日新月异，人们使用计算机和手机等工具均可很方便地对图像进行编辑处理，如图像缩放，亮度调整，改变对比度等。但是这也带来图像分类，检索等方面的问题。因此，研究者提出用图像哈希解决这一类问题。图像哈希指的是将图像单向映射为一串短小的数字序列，该数字序列可以是二进制数或者是十进制数，通过比较图像之间的哈希序列，可以有效地对图像进行分类，检索。图像哈希具有鲁棒性、区别性、安全性。鲁棒性是指原始图像经过保持数字内容的处理后生成的哈希序列应与原图像的哈希序列相同或者相似。区别性是指不同图像之间的哈希序列应有明显的不同，就是说不同图像的哈希序列的相似概率很小。安全性是指攻击者在不知道密钥的情况下无法生成正确的哈希序列。因此，图像哈希可应用于图像检索、图像取证和图像分类等方面。

近年来，不同的学者利用多种技术提出不同的哈希算法，其中按照数字图像处理方式可划分为基于图像变换和基于数据降维的方法：

1)基于图像变换的方法：文献[1]中Tang等人提出利用多维尺度分析MDS(Multidimensional scaling)构建图像哈希。该算法可以抵抗旋转攻击，不过效率还有提高的空间。文献[2]中Qin等人提出了一种基于显著性结构特征的图像哈希方案，该方案具有较好的鲁棒性，不过该算法容易遗漏一些局部信息，影响区别性。此外，还有利用小波变换DWT(discrete wavelet transform)计算哈希[3]，该算法效率较高。Tang等人提出了一种基于Random Gabor滤波和离散小波变换DWT的鲁棒图像哈希算法[4]，该算法对普通攻击具有较好的鲁棒性，不过对大角度旋转的鲁棒性比较差。

2)基于数据降维的方法：Tang等人在文献[5]中使用DCT和局部线性嵌入LLE(local linear embedding)来构建哈希序列。该算法对大角度的旋转鲁棒性较差。Tang等人提出基于张量分解TD(Tensor Decomposition)的图像哈希算法[6]，该算法的鲁棒性很好，效率也比较高，但是区别性还有提高的空间。文献[7]中利用四元数奇异值分解QSVD (quaternion singular value decomposition)来构建哈希序列，具有不错的效果。文献[8]Tang等人提出一种基于环分割和非负矩阵分解的图像哈希方案。该方案对JPEG压缩，旋转等攻击具有良好的鲁棒性。

此外，还有基于统计特征[9-11]、中心局部对称二值模式[12]、显著区域[13]、Zernike矩[14-15]、结构与梯度[16]、混合特征[17]等多种图像哈希算法。

上述哈希算法的哈希序列相对较长，并且大多数基于二维平面进行特征提取，而三维空间特征也非常重要。本文算法将二维平面特征与三维空间特征结合，减小了哈希序列长度，并且增强了哈希算法的鲁棒性和区别性。

与上述算法相比，本文算法有几点创新。第一，过去基于超像素分割的哈希算法是对整幅RGB或YCbCr图像进行超像素分割，这会导致生成的哈希序列较长，占用较多存储空间。本文哈希算法则是先提取图像亮度分量Y进行分块，再对每个小块进行超像素分割提取特征，这样可以减小哈希序列的长度，使哈希序列的存储空间变小。第二，以往的哈希算法大多数没有同时结合图像二维平面特征与三维空间特征，并且忽略三维空间的局部特征。本文算法以超像素分割和凸包算法得到的轮廓特征做为二维平面特征，图像分量所构建的三维空间中的局部距离特征做为三维空间特征。结合二维平面特征与三维空间特征得到最终哈希序列，使提取的特征更加全面，增强算法的区别性。最后本文算法与最新的基于三维空间特征的算法[16]以及另外基于二维平面特征较好的算法进行比较，仿真结果显示本文算法具有更好图像分类性能，并且还具有较短的哈希序列，因此本文算法所产生的哈希序列占用的存储空间较小。这说明本文所提出的结合二维平面特征与三维空间特征的哈希算法的性能要优于单一基于二维平面特征或是单一基于三维空间特征的哈希算法。同时本算法具有良好的密钥安全性，攻击者很难在没有正确密钥的情况下生成正确的哈希码。

2 提出的图像哈希方案

基于超像素分割和三维空间的图像哈希算法生成框图如图1所示。

2.1 图像预处理

首先将输入图像通过双线性内插法将其原始大小调整为N×N，这样可以让不同尺寸的图像具有相同的哈希长度，然后用高斯低通滤波处理，尽量减小噪声对哈希序列的影响。

图1 哈希算法流程图

2.2 提取位置信息

本文使用SLIC算法[18]对每个小块进行超像素分割提取位置信息，这样可以减小哈希序列的长度。首先将图像从RGB彩色空间转换为YCbCr颜色空间，在YCbCr空间中提取图像亮度图像Y分成大小相等不重叠的M×M个小块Y(i，j)，然后设定参数P将每一个小块Y(i，j)超像素分割为若干个像素集，提取这几个像素集中包含像素个数最多的像素集Yp(i，j)。其中i是小块在所在的行数，j是小块在所在的列数，1≤i≤M，1≤j≤M。

Yp(i，j)中包含所有像素的坐标集Yz(i，j)就是位置信息。每个小块中有(N/M)×(N/M)个像素，每个像素的坐标(x，y)由该像素在小块Y(i，j)中的行数x和列数y构成，其中1≤x≤(N/M)，1≤y≤(N/M)。

2.3 提取轮廓特征

本文利用凸包算法[19]从位置信息中提取轮廓特征，这样做的优点是可以用面积的形式表示出像素集在二维平面的分布状况。首先依次提取亮度图像的每个小块Y(i，j)中包含像素个数最多的像素集Yp(i，j)，用凸包算法计算出Yp(i，j)中所有像素形成的凸包面积Si，j，其中i为该小图像块的行数(1≤i≤M)，j为该小图像块的列数(1≤j≤M)。如图2所示，对图2中亮度分量Y(1，1)小块进行超像素分割后提取最大部分区域3内包含像素的坐标集Yz(1，1)，求出该坐标集合围成的四舍五入取整后的凸包面积S1，1。最后得出矩阵Si，j

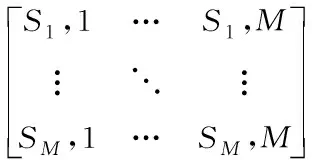
(1)

矩阵S是一个M行M列的矩阵，将其每一列依次连接再转置到得到一个一行M×M列的向量S(n)，其中1≤n≤M2，用其构建哈希序列H1

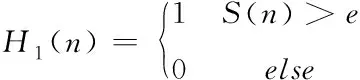
(2)

其中n=1，2，…，M2，e是S(n)的平均值。H1是由轮廓特征提取的哈希序列，长度为M2。

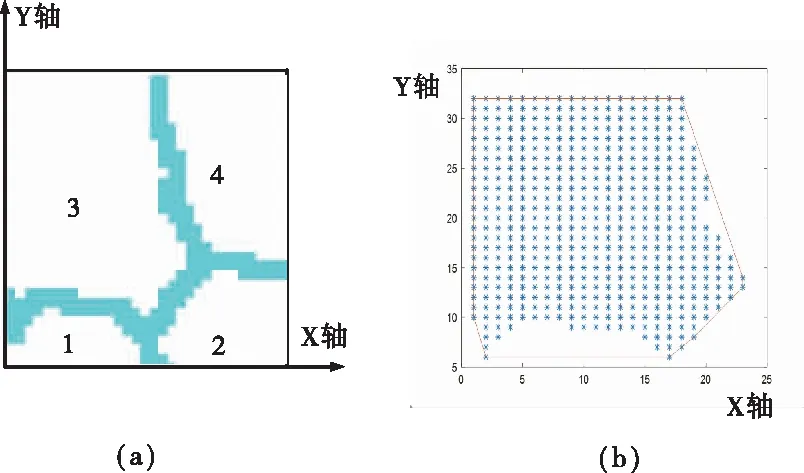
图2 求图像分量分成的小块内最大一部分3所包含的坐标围成的凸包

2.4 提取三维空间距离特征

以像素的行为x轴坐标，像素列为y轴坐标，以像素值为z轴坐标，可将图像构建为三维矩阵。图3(a)为亮度分量Y在三维空间中的形式。

本文将亮度分量Y分成大小相等不重叠的M×M个小块。为了构建三维坐标，分别以亮度分量Y所分成小块的行数i为x轴坐标，以亮度分量Y所分成小块的列数j为y轴坐标，由每个小块包含像素的平均值L(i，j)为z轴坐标，由此建立三维坐标系。则亮度图像Y位于M×M个小块中第i行第j列的小块Y(i，j)在三维空间中的坐标为(i，j，L(i，j))。图3(b)显示的是亮度图像Y分成的小块在三维空间中的坐标。

如图3(b)所示，亮度图像Y位于M×M个小块中第i行第j列的小块Y(i，j)，在三维空间中的坐标为(i，j，L(i，j))，与其相邻的三个小块在三维空间中的坐标为(i，j+1，L(i，j+1))，(i+1，j，L(i+1，j))，(i+1，j+1，L(i+1，j+1))。

再求出(i，j+1，L(i，j+1))，(i+1，j，L(i+1，j))，(i+1，j+1，L(i+1，j+1))三个点在三维空间中围成的三角形的重心坐标Oi，j，求出点(i，j，L(i，j))与Oi，j的距离D(i，j)构建空间距离特征。Oi，j的坐标为(xi，j，yi，j，zi，j)，其中xi，j，yi，j，zi，j的值分别如式(3)～(5)所示

xi，j=(i+i+1+i+1)÷3

(3)

yi，j=(j+1+j+j+1)÷3

(4)

zi，j=(L(i，j+1)+L(i+1，j)+L(i+1，j+1))÷3

(5)

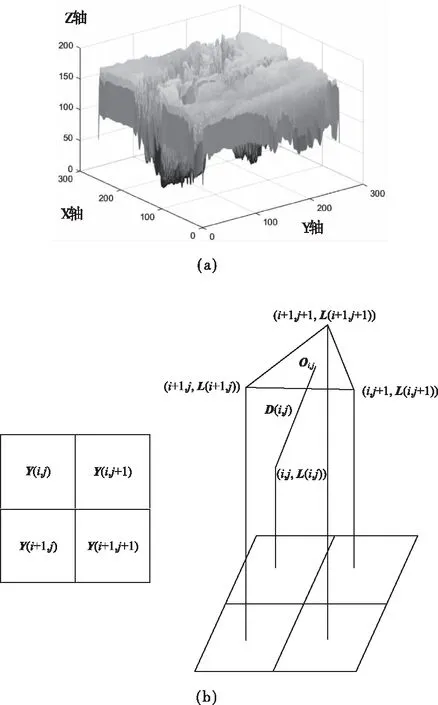
图3 (a)亮度分量Y在三维空间中的形式 (b)亮度分量Y分成的小块在三维空间中的坐标及距离特征的提取

最后求Y(i，j)在三维空间中的坐标为(i，j，L(i，j))与重心坐标Oi，j两个点在三维空间中的距离D(i，j)，D(i，j)如式(6)所示：

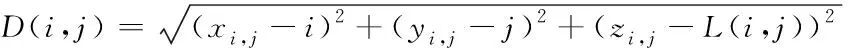
(6)

D(i，j)组成的矩阵D

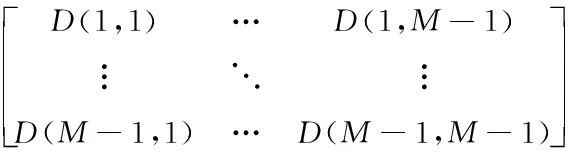
(7)

矩阵D是一个M-1行M-1列的矩阵，将其每一列依次连接再转置到得到一个一行(M-1)×(M-1)列的向量D(n1)，其中1≤n1≤(M-1)2，用其构建哈希序列H2

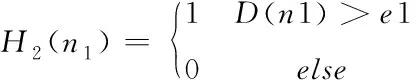
(8)

其中n1=1，2，…，(M-1)2，e1是D(n1)的平均值。则H2是由三维空间距离特征提取的哈希序列，长度为(M-1)2。

2.5 哈希生成

得到的两个特征组合成Hm=[H1H2]为中间哈希序列。由2.3节和2.4节可知本文所提哈希算法的哈希为长度C=M2+(M-1)2=2M2-2M+1位的二进制数。最后使用密钥对Hm进行置乱得到H，H为最终哈希序列。如(13)所示，当两幅图像汉明距离P大于阈值时判断为不同图像，反之判断为相似图像。

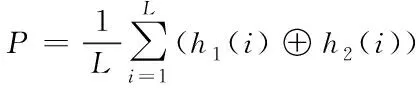
(9)

其中：h1和h2为两幅图像的哈希序列；⊕为异或符号。

3 实验结果及分析

本文算法的参数设置如下：归一化尺寸N=256，标准差为1的3×3的高斯低通滤波。分成小块的数量为M2=8×8=64，参数P=5，P是指对每个小块使用超像素分割时预创建超像素数。因此哈希长度为C=M2+(M-1)2=2M2-2M+1=113bits。本文实验均在一台2.30GHz Core i5-8300H，8GB内存，操作系统为windows 10的电脑上运行，编程平台为Matlab 2018b。

3.1 鲁棒性实验

用20幅图像作为样本进行鲁棒性实验，其中10幅如图4所示，样本图像依次按表1攻击类型生成相似图像。用本文算法得到这些相似图像的哈希序列，并依次计算这些哈希序列与原始图像的哈希序列之间的归一化汉明距离。根据攻击类别的不同，绘制原始图像与相似图像之间归一化汉明距离图，图5给出了其中5幅图像的鲁棒性实验结果，从图5中可以看出除旋转攻击之外的曲线波动范围较小，归一化汉明距离均小于0.13。而图像旋转攻击的实验结果中，汉明距离随角度的增加而增大。这是因为本算法对图像进行分块处理，因此对旋转攻击较敏感。表2为20幅图像在不同攻击下汉明距离的统计结果，可以看出在除旋转攻击外的实验结果中，归一化汉明距离最大值均小于0.13，平均值和标准差均小于0.06，而旋转攻击的最大值和均值均超过0.46。表示本文算法对除旋转攻击外的几种攻击，比图像缩放，高斯滤波等攻击具有很好的鲁棒性。

图4 彩色图像

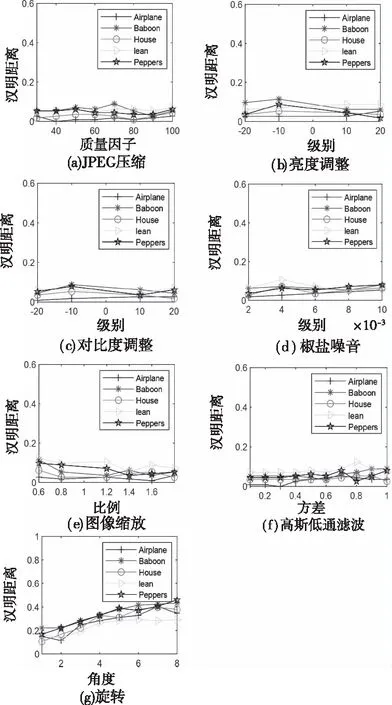
图5 鲁棒性实验

3.2 区别性实验

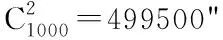
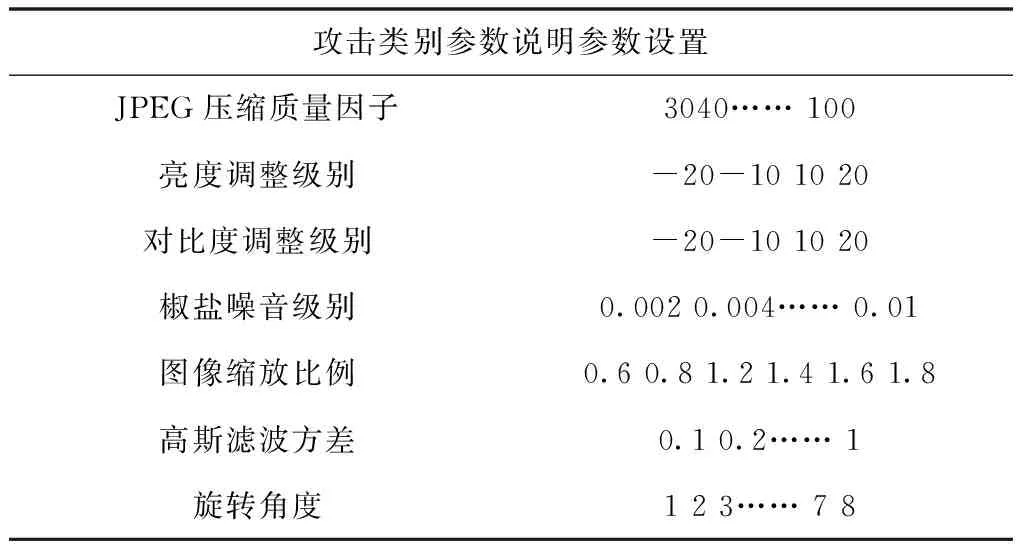
表1 鲁棒性实验中的攻击设置

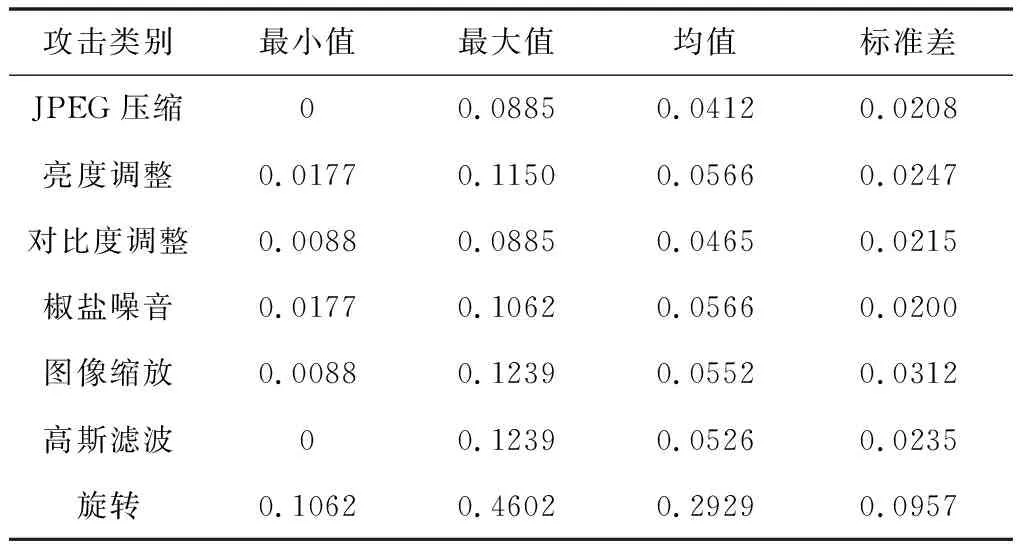
表2 不同攻击下的归一化汉明距离

图6表示这些图像对之间的归一化汉明距离分布及其概率分布，通过计算发现不同图像之间归一化汉明距离最小值为0.1770，相似图像对之间最归一化大汉明距离为0.2301，相似图像对和不同图像对归一化汉明距离的交集出现在0.1770和0.2301之间。为了获取最优阈值来区分相似图像对和不同图像对，本文引入碰撞率和检错率来分析本文算法的区别性，计算公式可为

(10)

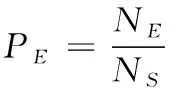
(11)

其中，NC表示不同图像对被错误判断为相似图像对的总数，NE表示相似图像对被检测为不同图像对的总数，ND表示不同图像对的总数，NS表示相似图像对的总数。PC和PE分别表示为碰撞率和检错率。

阈值选取的计算结果如表4所示，由其中数据可知，当阈值选取0.2124时，算法同时具有较低的碰撞率和检错率，区别性较好。

图6 归一化汉明距离与概率

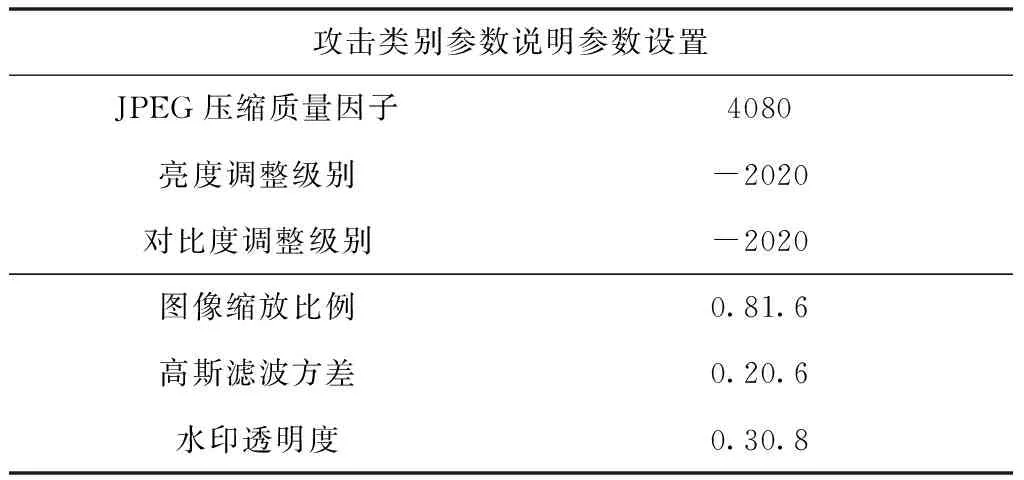
表3 区别性实验中的攻击设置

表4 阈值选取

3.3 安全性实验

哈希算法安全性是指由不同的密钥会产生不同的哈希序列。图7说明了本文哈希算法的密钥安全性，x轴是1000个错误密钥的索引，y轴是归一化汉明距离。从图中看出，所有错误密钥的归一化汉明距离最小值0.3363，平均值0.4750，均大于3.2选取的阈值0.2124，阈值如图中红线所示。说明如果得到的是错误密钥，几乎不可能计算出正确的哈希序列，因此本文算法具有不错的密钥安全性。

图7 正确与错误密钥的哈希值之间的归一化汉明距离

3.4 不同分块性能比较

为了分析对图像进行分块时，分块的数目对算法性能的影响，本文引入接收者操作特性曲线(ROC)进行性能比较，性能主要包括鲁棒性和区别性等。本节由不同的阈值计算出相应的错误接受率(PFPR)和正确接受率 (PTPR)，图8中的曲线显示其计算结果。图8中，横坐标为错误接受率PFPR，纵坐标为正确接受率PTPR，计算公式可表示为

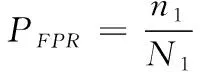
(12)

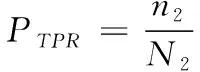
(13)

其中，n1代表的是图像对被误判为相似图像对的数目，n2代表的是图像对被正确判断为相似图像对的数目；N1代表所有不同图像对的数量，N2代表所有相似图像对的数量。显然，横坐标表示的是区别性的性能，纵坐标表示的是鲁棒性的性能，ROC曲线越靠近左上角表示性能越好。

在实验中，用1000幅图像进行区别性测试。按表3中的攻击设置，生成视觉上相似的图像，每幅图像可以生成12个相似图像。因此，相似图像对总数为78000个，不同图像对为499500个。当把图像分别分为4×4块，8×8块，16×16块时，本文算法哈希码长度分别25bit，113bit，481bit。当分为16×16块时，哈希长度较长，而且如表5所示，生成哈希码的平均时间较长，因此，实验中只选择比较图像分为4×4块和8×8块的哈希算法的性能。由图8可以看出，分为4×4块的曲线比分为8×8块的曲线更远离左上角，因此性能更差。本文哈希算法选择把图像分为8×8块是在鲁棒性和区别性之间平衡的一个较好的选择。

表5 不同分块时间比较

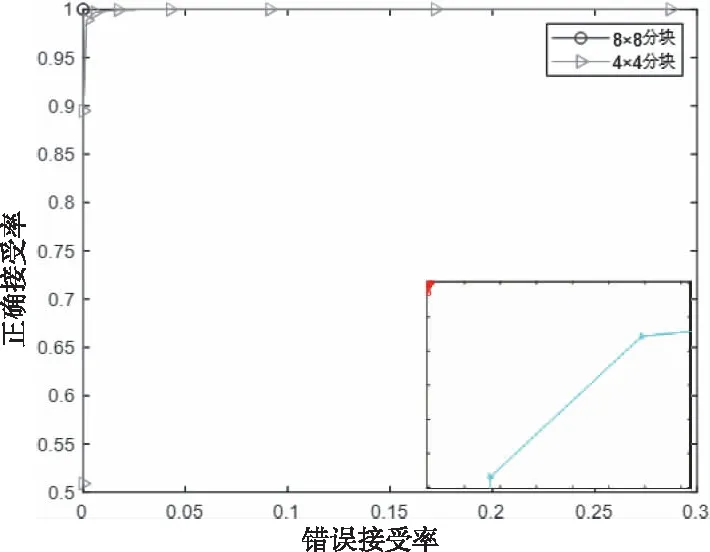
图8 不同分块的ROC曲线

3.5 不同参数性能比较

为了分析对图像分成的每个小块进行超像素分割时，设置的参数P对算法性能的影响，本节与3.4节相同，引入接收者操作特性曲线(ROC)进行性能比较，性能主要包括鲁棒性和区别性等。本节由不同的阈值计算出相应的错误接受率(PFPR)和正确接受率(PTPR)，图9中的曲线显示其计算结果。图9中，横坐标为错误接受率PFPR，纵坐标为正确接受率PTPR，计算公式与3.4节相同，可表示为式(16) (17)。

在实验中，用1000幅图像进行区别性测试。按表3中的攻击设置，生成视觉上相似的图像，每幅图像可以生成12个相似图像。因此，相似图像对总数为78000个，不同图像对为499500个。本节讨论当对图像分成的每个小块进行超像素分割时，设置的不同参数对算法性能的影响，该参数P表示的是对每个小块使用超像素分割时预创建超像素数。本节比较三个参数，分别为P=1，5，9时算法的性能。

由图9可以看出，参数设置为5的哈希算法的ROC曲线比参数设置为1，9的哈希算法的ROC曲线更靠近左上角，所以性能更好。本文哈希算法选择参数P=5，把超像素分割参数设置在5是在鲁棒性和区别性之间平衡的一个较好的选择。

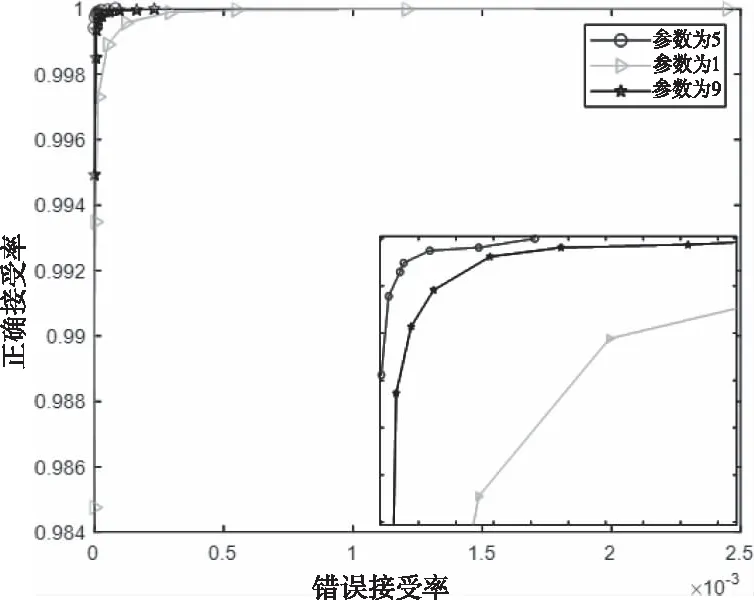
图9 不同参数的ROC曲线

3.6 不同算法性能比较

为了比较哈希算法的性能，本文算法与SG算法[16]，TD算法[6]，CVA-Canny算法[10]和Ring算法[9]进行了比较。比较的参数与各自发表的论文中设置的参数相同，所比较的算法哈希长度分别为156位二进制数，96位二进制数，40个十进制数(至少160位)和440位二进制数。本文提出的哈希算法的哈希码长度是113位二进制数，仅稍长于TD算法。因此本文哈希算法与对比算法比较，在具有更优的鲁棒性和区别性的同时，具有更短的哈希码，存储本文算法产生的哈希码的储存空间较小。

在这个实验中，与3.4节相同，用本文的算法计算相似图像对与不同图像对生成的哈希序列，并计算这些序列之间的距离。相似图像的攻击设置也和表3一样。其中，相似图像对总数78000个，不同图像对总数499500个。与前文相同，由不同的阈值计算出相应的错误接受率(PFPR)和正确接受率(PTPR)，图10中的曲线显示其计算结果。可以看出，本文算法的ROC曲线比别的算法更加靠近左上角，说明本文算法的分类效果较好。

表6 不同算法性能比较

SG算法[16]，TD算法[6]，CVA-Canny算法[10]，Ring算法[9]哈希码计算的平均时间分别为0.014s，0.103s，0.284s，0.214s。本文算法提取了亮度分量Y并进行分块，并对每个小块进行超像素分割，因此哈希计算平均时间较长。

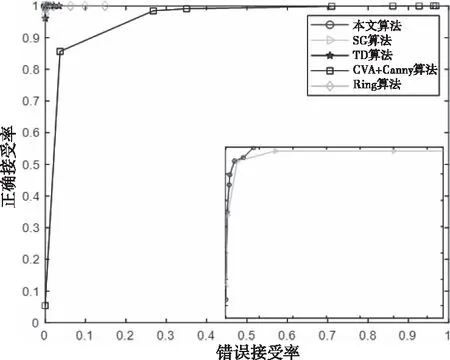
图10 不同算法的ROC曲线

4 结语

图像的三维空间特征容易在图像哈希算法中被忽视，影响算法性能。为了充分利用图像二维平面特征与三维空间距离特征，本文利用超像素分割与凸包算法提取二维平面特征，显著地缩小哈希序列的长度，再结合图像三维空间特征，提高算法性能。

仿真结果表明，本文算法对高斯滤波，图像缩放等多种攻击具有良好的鲁棒性；ROC曲线表明本文算法与对比算法相比具有更好的图像分类性能；本文算法在具有良好的安全性的同时哈希长度仅为113位二进制数，小于大多数哈希算法，说明本文算法产生的哈希序列需要的存储空间较小。不过本文算法存在计算平均时间稍长的缺点，在下一步工作中，应着重考虑在保留原有的良好性能的基础上，优化算法结构，减少哈希计算的平均时间，使算法性能进一步提高。