基于TSNE及改进灰色关联的输电工程造价预测

宋晓华，汪 鹏，张 露，寇英芳

(1. 华北电力大学经济与管理学院，北京 102206；2. 华北电力大学新能源电力与低碳发展研究北京市重点实验室，北京 102206；3. 国网北京市电力公司，北京 100031)

1 引言

近年来，电网输电工程建设的规模和强度持续增加，对工程造价提出了更为严格的要求[1]。高效、精确地预测输电工程造价，对电网造价精细化控制、基建投资效益提升具有重要意义[2]。国内针对输电工程造价预测仍然存在一些不足。文献[3]从人力运输的角度分析其对造价以及各部分工程造价比例的影响。文献[4]将地质划分与输电工程定额对应，并开展了地质划分对造价影响分析。文献[5]从风速、覆冰等角度对架空输电工程造价敏感因素进行了理论分析，但并未考虑不同工程参数下工程量之间的差异。文献[6]对甘肃地区±800千伏特高压线路造价影响因素指标进行相关性分析，筛选影响造价的关键指标，但并未对指标非线性关系进行深入研究。文献[7]提出讨论K-Means聚类、层次聚类、模糊聚类3种聚类方法，所提出的方法针对非线性相关性指标聚类效果不佳。文献[8]构建输电工程造价指数，采用灰色预测模型开展预测，考虑人材机价格动态变化，但并未兼顾施工水平对造价的影响。文献[9]提出采用灰关联分析与粒子群优化的支持向量回归模型，对工程造价进行预测。综上所述，目前的研究关注单一参数的影响分析，并未考虑构建综合的预测指标体系。针对指标体系重叠信息的处理，多考虑线性指标的降维，而未充分考虑如何同时处理线性、非线性工程量指标信息重叠问题。利用灰色关联算法进行优选时，多采用算数均值进行关联度计算，未考虑指标之间的信息差异及设备材料价格随时间的动态变化。因此，本文提出基于TSNE及改进灰色关联的输电工程造价预测模型。首先，从多元工程参数、工程量指标体系构建影响工程造价的指标体系。其次，提出TSNE流行可视化降维方法，将高维工程量指标数据分布映射到低维流行结构。在此基础之上，建立改进灰色关联度的量价双维时空相似特征优选模型：在空间维度上，考虑工程参数及工程量指标的相似程度；在时间维度上，考虑人材机及设备价格随时间的动态变化。此外，考虑到我国输电工程造价构成主要基于定额体系，兼顾施工生产力水平差异，基于造价统计分布特性，采用abm方法对优选后的样本工程造价进行均值特性强化，使之能更好体现平均造价水平。最后，进行仿真，验证模型的有效性。

2 基于TSNE及改进灰色关联预测模型

2.1 输电工程造价预测指标体系

输电工程本体造价由基础工程、杆塔工程、接地工程、架线工程、附件工程、辅助工程六个单位工程构成[10]。工程参数、工程量指标共同影响输电工程造价。其中，接地工程、辅助工程只占本体工程造价的2%-4%，费用占比较小，对工程量指标进行初步筛选，剔除接地土方、排水沟等对本体工程造价影响不大的工程量指标，形成输电工程造价预测指标体系，如图1。

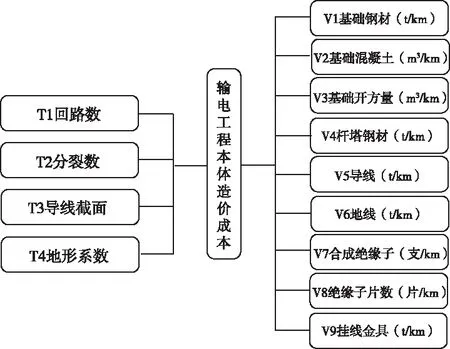
图1 输电工程造价预测指标体系

2.2 基于TSNE的工程量指标降维处理

对110kV输电工程造价指标进行相关性分析，结果如图2。

图2 样本数据变量散点图矩阵图

从图2分析，基础钢材(V1)、基础混凝土(V2)、基础开方(V3)、杆塔钢材(V4)等指标之间存在一定程度的线性相关，其它指标存在非线性相关。因此，需要对指标进行降维处理，消除指标数据的重叠信息。主成分分析(PCA)是一种常见的指标降维处理方法，可以解决指标之间的共线性问题，但PCA属于线性降维的方法，对非线性指标处理效果不佳。流行可视化降维算法能够较好地在低维空间采用可视化的方式表达高维指标数据的内部结构关系。典型的流可视化降维方法有随机邻域嵌入(SNE)、T分布随机邻域嵌入(TSNE)等。SNE存在样本数部分布拥挤问题，TSNE采用联合概率表示点对应的相似度，通过优化两个分布之间的距离散度，得到低维空间的样本分布，能够有效解决数据拥挤问题。由此，本文提出基于TSNE的工程量指标降维处理算法。

2.2.1 TSNE降维算法的基本原理

1)SNE算法的基本原理

设工程量指标的高维数据点为X=(x1，x2…，xn)，低维映射Y=(y1，y2…，yn)。

高维空间、低维空间的概率可以表示为pi|j、qj|i，计算公式如(1)、(2)所示。

(1)

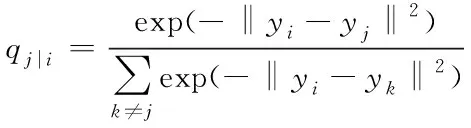
(2)

为衡量高维工程量指标空间和低维工程量指标空间的相似程度，引入代价函数KL散度，计算公式为：

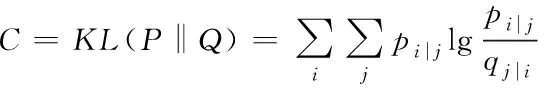
(3)

将代价函数对低维气象点进行求导得：

(4)

2)TSNE算法的基本原理

TSNE将低维指标数据Y和原始高维指标数据X的条件概率改进为对称的联合概率密度，即

pi|j=pj|i，qj|i=qi|j

(5)

计算高维之间的联合概率密度

(6)

低维样本的联合概率密度

(7)

建立新的代价函数为

(8)

对代价函数C进行寻优，更新规则为

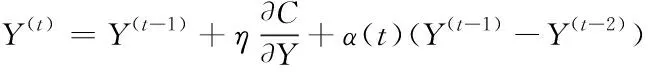
(9)

式中，Y(t)是低维空间的样本数据，t是迭代次数，η表示学习率，α(t)为动量因子。

2.2.2 PCA、TSNE仿真

为了验证TSNE对工程量指标的降维效果。对工程量指标分别采用PCA、TSNE算法进行降维计算。

图3 PCA和TSNE算法仿真对比

对比分析图3，与PCA降维效果相比，TSNE算法对四个电压等级的样本工程实现了较好的分类，各个电压等级的样本边界明晰，算法降维效果较好。

2.3 基于改进灰色关联的相似特征优选方法

基于工程参数指标以及工程量指标(不降维、PCA降维、TSNE降维)形成新的预测体系，新的预测指标体系为

F=(F1，F2，…，Fj) (j=1，2，…，p)

(10)

令F=Gi=(gi(1)，gi(2)，…gi(j))，其中，i=0，1，…n，j=1，2…p。计算灰色关联系数，如式(11)所示

(11)

其中

Δqj=|g0(j)-gq(j)|

Δmin=minqminjΔqj，Δmax=maxqmaxjΔqj

式(11)中，ρ为分辨系数。利用熵值法及权重计算公式如式(12)、(13)所示。

(12)

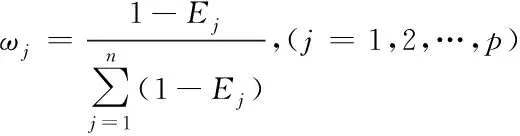
(13)

熵权修正的灰色关联度计算公式为

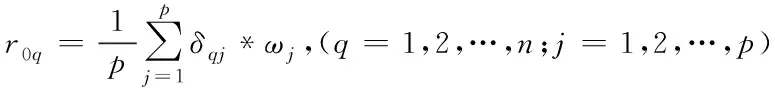
(14)

时间因子权重系数计算方法为

(15)

式(15)中，tq为待预测工程施工日期与第q个样本工程施工日期之间的天数；int为取整运算符；α1、α2、α3分别为日衰减、周衰减和年衰减系数；N1、N2、N3为常数。经过时间因子修正以后的灰色关联度为

R0q=r0qf0q

(16)

2.4 基于统计分布的造价均值强化算法

将灰色关联度模型优选后的样本造价进行算数平均处理是常见的一种均值处理方法，考虑到我国输电工程安装费用计算基于定额体系，定额消耗量反映的是社会平均施工生产力水平[10]，为兼顾先进施工生产力水平与落后施工生产力水平差异，本文提出基于统计分布的造价均值强化算法。

2.4.1 输电工程本体投资统计分布分析

对110kV输电工程造价进行研究，绘制造价散点图及高斯分布，如图4所示。

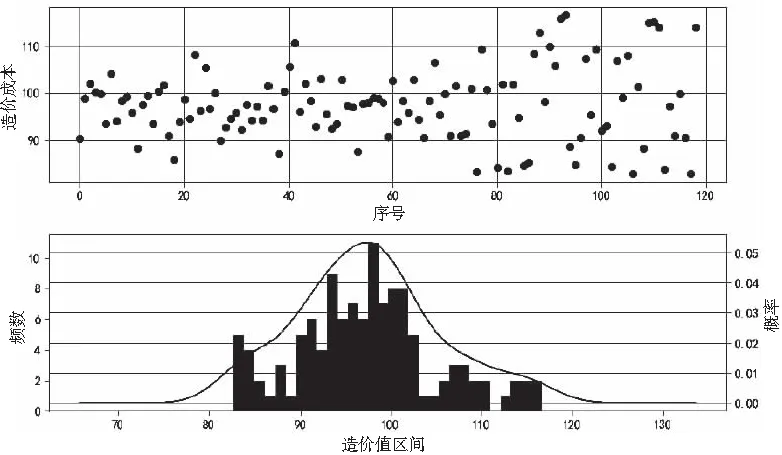
图4 110kV输电工程造价散点图及高斯分布

由图4，可以判别其大致属于正态分布。为了进一步验证正态分布假设，本文采用夏皮罗-威尔克进行检验。检验统计量为0.9803、P值为0.0797，统计量接近于1，P值显著大于0.05，无法拒绝其符合正态分布。同理，对220kV、330kV、500kV输电工程本体造价进行检验，结果也表明其服从正态分布规律。

2.4.2 abm均值强化算法

将改进灰色关联算法优选后的工程造价数据按大小顺序排列，求出该组数据的算术平均值，此即一般值m，表示样本集所代表的平均造价水平。根据二次平均法的原理，再对该组数据中小于m的值求算数平均得到x3，对该组数据中大于m的值求平均得到x4。定义先进值a为一般值m和平均值x3的算术平均值，先进值表示输电工程造价水平较低者的平均水平；同理，保守值b为一般值m和x4和平均值的算术平均值，表示输电工程造价水平较高者的平均水平。

(17)

根据正态分布的规律来分析，先进值、一般值、保守值占全部数据的比例大致接近1：4：1，均值计算方法如式(18)所示。

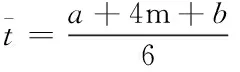
(18)

3 仿真分析

收集我国各省区已经完成结算的204项110kV-500kV输电工程造价作为数据样本。从三个方面进行仿真分析：1)分析灰色关联与改进灰色关联模型预测误差，验证改进灰色关联模型的预测效果。2)分析TSNE、PCA与灰色关联、改进灰色关联结合下的预测误差，验证TSNE降维算法对预测效果提升作用。3)分析不同电压等级输电工程预测误差，验证预测方法针对不同对象的预测效果。

1)灰色关联与改进灰色关联模型对比仿真

将传统灰色关联模型+算数均值预测模型和本文提出的改进灰色关联模型+算数均值、改进灰色关联+abm均值模型的预测效果进行对比分析，研究对象为110kV输电工程，改进灰色关联输入的工程量指标不作降维处理。由图5，改进灰色关联+abm均值的预测模型数据对真实值拟合程度更好。

图5 灰色关联模型与改进灰色关联模型预测仿真

计算平均绝对百分比误差(tMAPE)，计算结果如表1所示。

表1 灰色关联与改进灰色关联模型仿真误差结果

改进灰色关联模型+算数均值误差较传统灰色关联模型+算数均值降低2.81%，表明改进灰色关联方法能够有效提升预测精度，这得益于改进灰色关联方法在工程参数及工程量相似特征筛选的基础上，进一步挖掘了不同工程之间人工、材料、机械以及设备价格随时间的动态变化。

改进灰色关联模型+abm均值较改进灰色关联模型+算数均值误差降低0.82%，表明abm均值较算数均值能够提高一定的预测精度，这是因为abm均值方法基于统计分布规律，兼顾了施工生产力水平差异，更符合输电工程造价实际情况。

在工程量指标不降维的情况下，改进灰色关联+abm均值模型误差较另外两种方法最低，预测效果相对较好，但部分样本点的预测值与结算实际值偏差较大，且不满足输电工程造价5%-8%的误差要求，预测精度仍有提升空间。

2)不同降维方法下的模型对比仿真

本节将PCA、TSNE降维算法与灰色关联模型+算数均值、改进灰色关联模型+算数均值、改进灰色关联+abm均值模型结合，并进行仿真分析，结果如图6所示。

图6 融合降维算法的灰色关联、改进灰色关联预测仿真

计算各预测模型的平均绝对百分比误差，计算结果如表2、表3所示。

表2 PCA+灰色关联、改进灰色关联模型仿真误差结果

表3 TSNE+灰色关联、改进灰色关联模型仿真误差结果

对比分析表1、2、3，采用PCA、TSNE降维算法均能提升预测精度，这是因为降维能够有效降低工程量指标中的信息重叠，提升灰色关联或改进灰色关联对多维指标向量的适应性。同时，由于TSNE对非线性数据的处理效果较佳，降维效果比PCA的更好。

本文提出的TSNE+改进灰色关联+abm均值模型预测误差为3.19%，且多数样本的预测值与结算实际值误差小于5%，误差较为集中，模型预测效果最为理想。

3)220kV、330kV、500kV输电工程造价预测对比仿真

计算得到三个电压等级输电工程造价预测平均绝对百分比误差分别为2.91%、2.74%、2.56%。结果表明，本文提出的方法针对不同电压等级的输电工程也具有较好的预测效果。

4 结论

本文构建了输电工程造价预测指标体系，设计了基于TSNE的工程量指标降维算法，建立了基于改进灰色关联度的量价双维时空相似特征优选模型，提出了基于abm的均值强化算法。仿真结果表明，110kV、220kV、330kV、500kV输电工程造价预测值与结算实际值的误差分别为3.19%、2.91%、2.74%、2.56%，具有较好的预测效果。