共轴式直升机建模与基于ESO的LTV MPC设计

黄扬炼，双 丰，周 翔

(广西大学电气工程学院，广西 南宁 530004)

1 引言

随着智能控制技术在无人直升机控制中的应用，无人直升机作为人工智能设备逐渐出现在大众的视野之内，无人直升机的应用领域涉及军工[1]、农业[2]、商用[3]和救援救灾[4]等方面。无人直升机的应用如此广泛，是建立在良好的姿态控制基础上的，因此研究直升机的姿态控制具有重要意义。

经典的直升机姿态控制算法中有PID[5]、LQR[6]和H∞等[7]线性控制方法，但这些方法只能满足直升机悬停点附近或小机动下的飞行性能，文献[8]设计的增益调度控制算法虽然可以满足直升机的全包线飞行但会出现抖振现象。近年来，MPC算法因为能有效地处理多变量、有约束的问题被广泛应用于直升机控制中。文献[9，10]以悬停点的LTI模型作为预测模型为直升机设计的LTIMPC控制器，在直升机离开悬停点或高机动飞行时会出现预测模型失配。文献[11]利用非线性模型作为预测模型为四旋翼设计的NMPC控制器虽然解决了预测模型失配问题，但因其计算复杂度高而无法轻易实现。文献[12]用线性时变(LTV)模型作为预测模型，为直升机设计了LTV MPC控制器，相比NMPC来说该算法复杂度降低但没考虑扰动问题。在抗扰动控制器设计方面，文献[13]为四旋翼设计的ADRC控制器只适用于扰动量与控制量在同一通道的系统，而直升机的外扰动与控制量一般不在同一个通道。文献[14，15]结合ESO与MPC为直升机设计了控制器，文献[14]直接用控制量对ESO观测到的扰动进行前馈补偿会导致控制量饱和而无法完全补偿大扰动问题。文献[15]利用ESO观测到的扰动与系统模型相结合但MPC中的预测模型采用的仍是LTI模型。

与文献[14，15]的方法不同，本文提出的ESO+LTVMPC控制算法结合了ADRC和LTV MPC算法的优点，利用ESO观测到的扰动力矩补充到非线性模型中并线性化得到LTV模型，并将此LTV模型作为MPC的预测模型为直升机设计LTVMPC控制器。最后将本文设计的ESO+LTVMPC算法与PID、LTI MPC和LTV MPC算法进行姿态跟踪和抗风扰仿真对比。

2 共轴直升机的非线性数学建模

本文的研究对象为小型无人共轴双旋翼直升机，根据机理建模法可以得到共轴式直升机的非线性数学模型。

根据文献[16]，把直升机当作刚体，直升机的运动学模型可以描述为

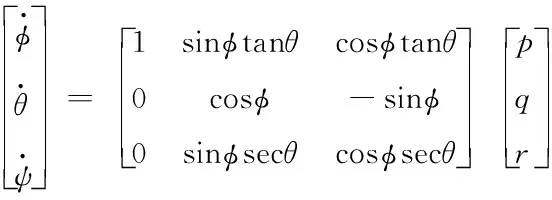
(1)

式中φ，θ，ψ是欧拉角；p，q，r是机体轴系下的角速度。

直升机的刚体动力学模型可以由牛顿-欧拉方程描述，具体表达式为

(2)

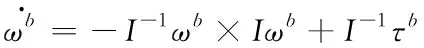
(3)

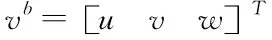
上旋翼桨叶的挥舞运动是一个比较复杂的非线性耦合系统，根据文献[19]旋翼的挥舞运动方程可以表示为

(4)

其中，Abs、Bas分别是纵、横向挥舞运动间的耦合效应系数，τ是上旋翼挥舞运动时间常数，它们的具体计算表达式可以参考文献[19]；δlon、δlat为倾斜盘的横、纵向输入，Alon是δlon到桨叶横向周期变距角的放大倍数，Blat是δlat到桨叶纵向周期变距角的放大倍数。

联立式(1)到式(4)，整理得到共轴双旋翼直升机的非线性数学模型为

(5)

根据式(5)，本文研究的共轴双旋翼直升机的非线性数学模型结构如图1所示，直升机的非线性数学模型参数如表1所示。

表1 模型参数

图1 模型结构

为了验证本文建立的非线性数学模型与真实直升机动态的关系，根据式(5)在simulink中搭建直升机的仿真模型，在相同PID控制器参数和相同的姿态参考值下，对比仿真模型的输出曲线与直升机的真实飞行动态曲线，对比结果如图2所示。俯仰角与横滚角的仿真结果类似。

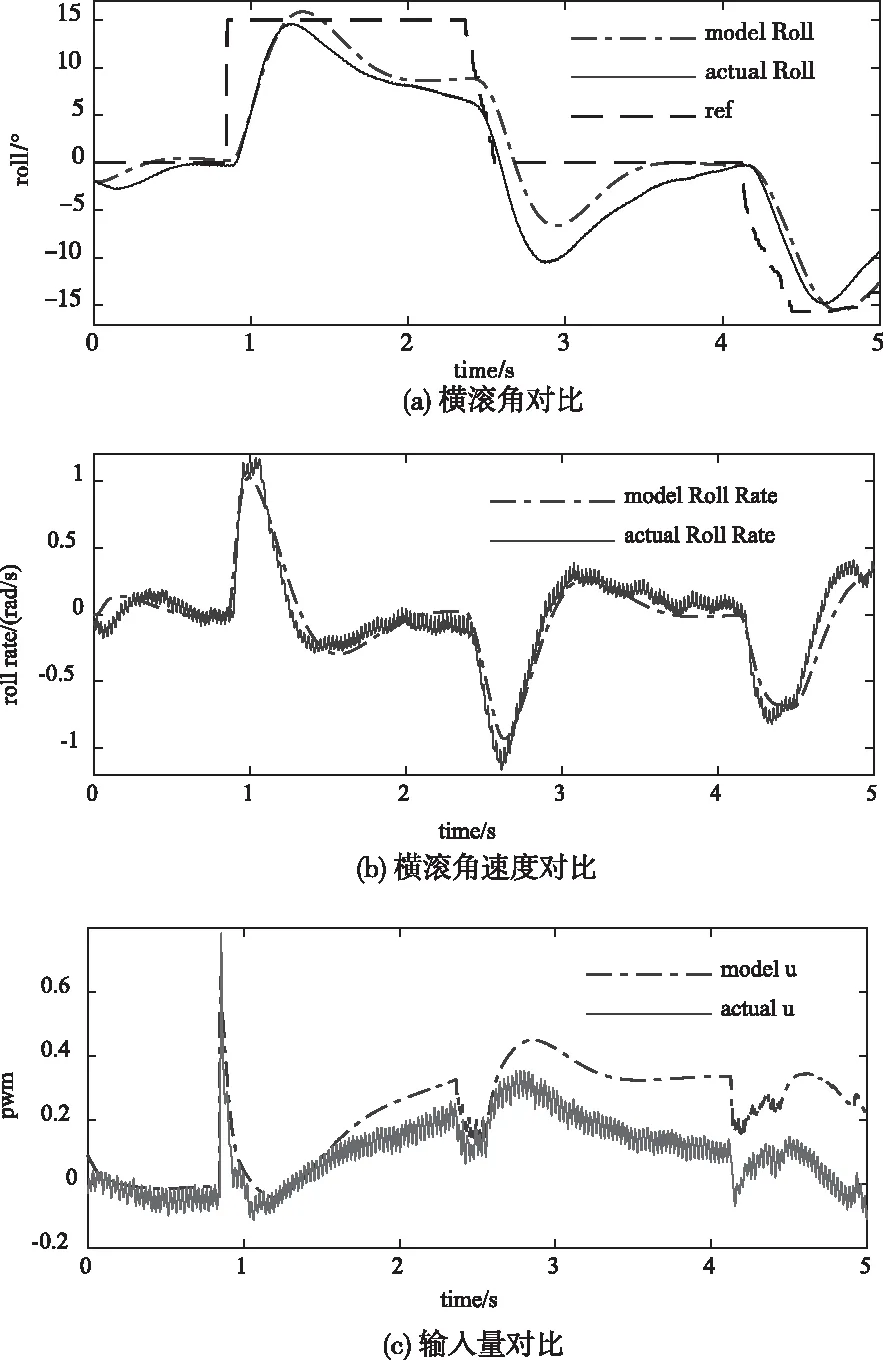
图2 模型验证

由图2可知，本文所建立的共轴直升机非线性数学模型很好地体现了直升机的真实动态，可以用于控制器设计和仿真。

3 ESO设计

为了降低ESO的阶次，分别为横滚通道和俯仰通道设计各自的ESO。以横滚通道为例，首先从式(5)中提取出横滚姿态模型，并展开为如下形式

(6)

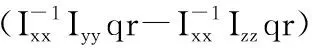
(7)

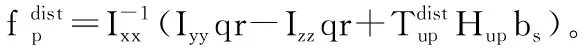
(8)

其中

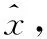
(9)

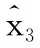
V=[p1，p2，p3，p4]； Lroll=(place(Aroll′，C′，V))′；

俯仰通道ESO的设计方法与横滚通道的设计方法类似，这里不再赘述。为了第3节中对俯仰ESO观测值的使用，记3为as的观测值，4为的观测值。

4 基于ESO的LTV姿态模型

不考虑偏航通道，从式(5)中提取出共轴直升机的非线性姿态模型，根据第2节中的假设(4)和假设(6)可以将非线性姿态模型化为

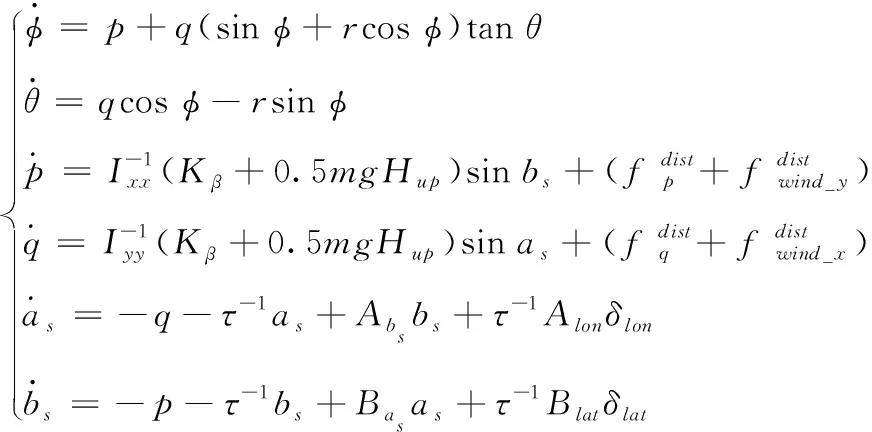
(10)

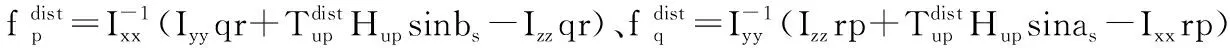
令x(t)=[φ，θ，p，q，as，bs]T，u(t)=[δlon，δlat]T将式(10)写成如下形式

(11)

将式(11)进一步线性化。将式(11)在t0时刻对应的系统运行点(x(t0)，u(t0))附近进行一阶泰勒展开，得到：

(12)

(13)

令可测量状态向量η=[φ，θ，p，q，r]T，采样周期为T，则式(13)中的系数矩阵计算方法如下

5 LTV MPC算法设计

LTVMPC与LTIMPC算法的唯一区别是，LTVMPC算法中的预测模型是线性时变的，而LTIMPC算法的预测模型是线性时不变的。因此，当系统运行偏离平衡点较远时，MPC算法常常会发生预测模型失配的现象，导致控制性能下降，而LTVMPC算法的预测模型是线性时变模型，随着系统工作点的变化而变化，所以LTVMPC算法基本上不会出现预测模型失配现象。

第3节已经求得直升机的LTV模型，以此LTV模型作为预测模型设计LTVMPC姿态控制器。一般情况下，LTVMPC算法的目标函数取如下形式

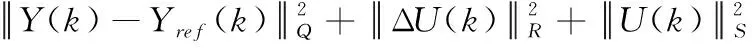
(14)

其中，Y(k)是预测矩阵，可以根据式(13)求得。ΔU(k)是控制增量矩阵，Yref(k)是参考值矩阵，U(k)是控制矩阵，它们的具体表达式可以参考文献[20]。ε是防止式(14)无法求得最优解而引入的松弛因子。ρ、Q、R 和S 为权重矩阵。

根据文献[21]的方法可以将目标函数式(14)化为标准二次型形式

(15)

其中，系数矩阵Hk、Gk、Pk、N、S、Mmin、Mmax的具体表达式可以参考文献[21]。求解一个ΔU(k)使得目标函数式(15)最小是一个标准二次规划问题，本文使用matlab的quadprog函数求解式(15)。求得的ΔU(k)即LTVMPC算法在控制时域内的最优控制序列，取该序列的第一个元素作为k时刻的控制量作用于系统。

6 数值仿真分析

本文设计的ESO+LTVMPC姿态控制算法的控制结构如图3所示。为了进行对比实验，另外设计离散串联PID算法、LTIMPC算法、LTVMPC算法，并给出对比实验结果。

ESO+LTVMPC姿态控制算法中，横滚ESO和俯仰ESO的闭环极点取V=[-10-25i，-10+25i，-180-15i，-180+15i]；线性时变模型预测控制算法的权重矩阵取Q=diag(17，17，1，1)，R=diag(0.5，0.5)，ρ=2，S=diag(0.1，0.1)；预测时域P=20；控制时域M=2；采样时间T=0.0025s；期望角速率pr=qr≡0。

离散串联PID姿态控制算法的角度环的PI参数取P=5，I=2；角速度环的PID参数取P=0.6，I=3，D=0.001。

LTIMPC算法、LTVMPC算法的各参数与ESO+LTVMPC算法的参数保持相同。MPC算法的预测模型取直升机悬停点的LTI模型，LTVMPC算法的预测模型取无ESO补充值的LTV模型。

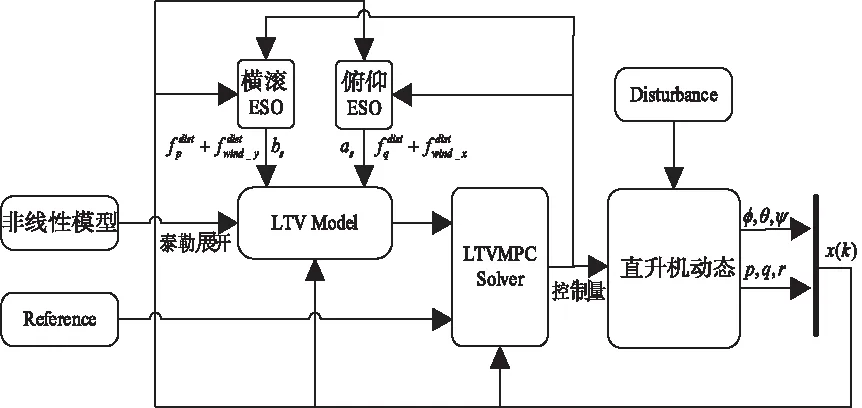
图3 控制结构图

对上述4种算法做4组不同的仿真，4组实验的实验内容比较如表2所示。另外，由于俯仰角的仿真结果与横滚角的仿真结果相似，下面只给出横滚角的仿真结果。

表2 实验内容比较

图4 风扰为正弦波下的横滚角仿真结果

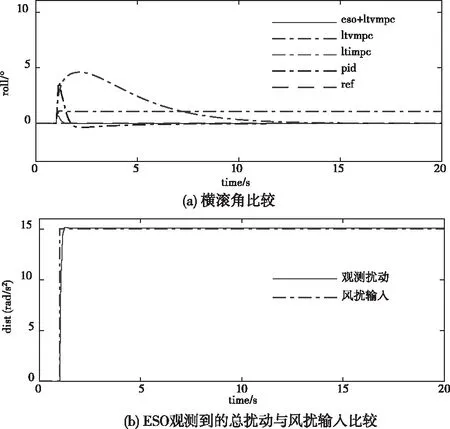
图5 风扰为阶跃波下的横滚角仿真结果

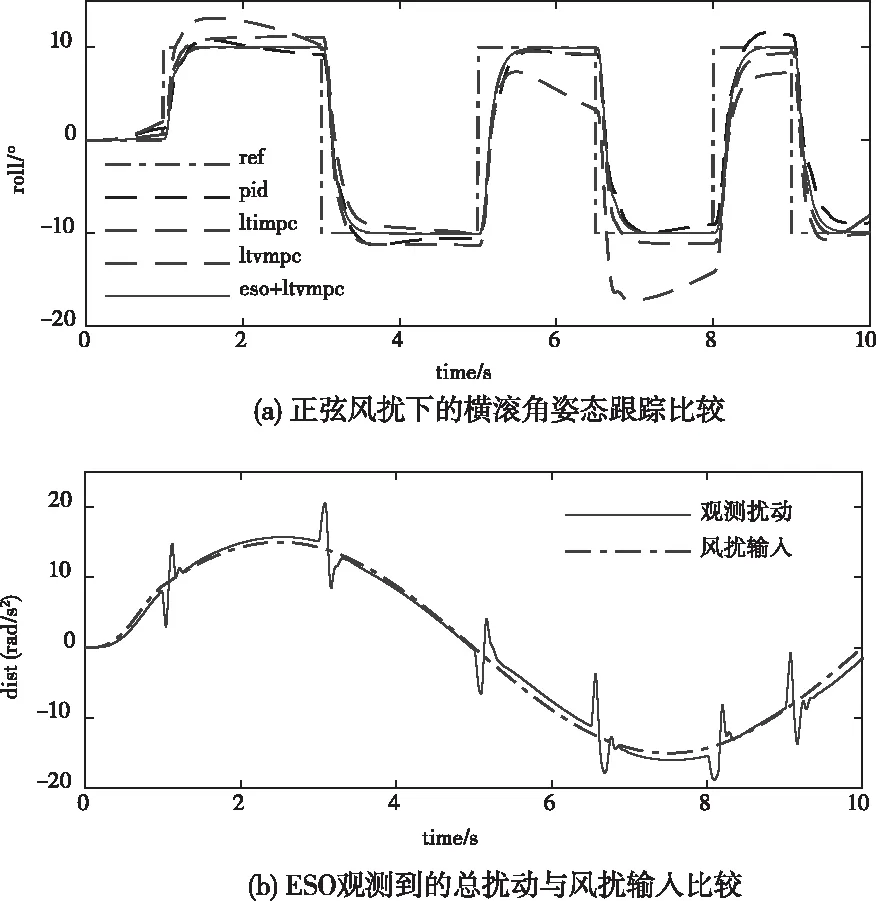
图6 风扰为正弦波横滚角参考值为矩形波的仿真结果

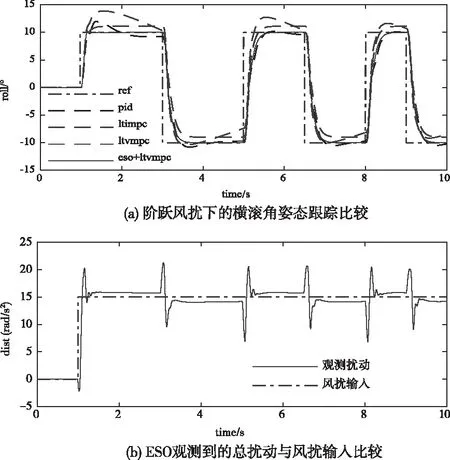
图7 风扰为阶跃波横滚角参考值为矩形波的仿真结果

由图4和图5可知，在正弦波或者阶跃波风扰条件下，ESO+LTVMPC算法的抗干扰能力是最强的，能够迅速抑制扰动并回到0位置，而其它算法会产生不同程度的等幅震荡或衰减震荡。由图6和图7可知，ESO+LTVMPC算法在正弦风扰或者阶跃风扰力矩作用下的姿态跟踪性能是最好的，几乎可以达到无静差无超调地跟踪参考值，而其它算法会产生静差和超调，LTIMPC算法因为预测模型失配的原因控制效果最差。在所有实验中ESO则很好的观测到了总扰动，由于ESO观测到的是总扰动(内扰动+外界风扰)，因此，总扰动与风扰输入曲线存在轻微的差异。

7 结论

把直升机当作刚体，通过机理建模得到了共轴式直升机的非线性数学模型，并通过直升机实际飞行数据验证了所建立模型的可行性。

假设外界风扰作为一个力矩项只直接作用于角速度通道，设计了ESO观测系统所受的扰动力矩并补充到直升机非线性微分方程中，对补充扰动力矩后的微分方程进行泰勒展开得到了直升机的LTV模型，基于此模型设计了LTVMPC姿态控制器，并将LTVMPC问题转化为QP问题进行求解。

设计了串联离散PID、LTIMPC、LTVMPC算法与本文算法进行仿真对比，验证了本文设计的ESO+LTVMPC姿态控制算法的抗扰动能力和姿态跟踪能力。

本文设计的ESO+LTVMPC算法拥有很好的姿态跟踪性能和抗干扰能力，但是也存在一些不足。第一，该算法中的ESO模块对传感器噪声是比较敏感的；第二，算法中需要调节的参数相比PID或者LTIMPC算法要多；第三，算法结构复杂。因此，作者下一步的工作计划，主要侧重于算法的参数如何快速整定问题、硬件平台的算法实施和传感器滤波等问题。