三维块单元惯性释放方法研究
王宇帆, 刘 虓, 陈超核
(华南理工大学土木与交通学院,广州 510640)
1 前言
航行中的船舶、飞行中的飞机、行驶中的汽车均属于自由无约束结构,采用有限元法对此类结构进行静力分析时,仍需要施加约束来消除刚度矩阵的奇异。当此类结构受到的外载荷满足静力平衡条件时,求解后约束点处的支反力为零;由于在载荷的计算和施加过程中存在诸多近似,很难得到绝对平衡力系,约束点处产生的支反力会改变结构的实际受力状态,引起局部应力集中、变形失真、传力路径错误等异常现象。为解决这一问题,研究人员将惯性释放技术引入此类结构的有限元强度计算中,这是一种基于达朗贝尔原理的惯性平衡技术,它首先计算结构体在不平衡外载荷下产生的加速度,再根据加速度计算出惯性载荷,最后将惯性载荷与外载荷叠加从而使结构体达到静态平衡。
商用有限元软件MSC、ANSYS、ABAQUS 中均具备该功能,被广泛应用于船舶、航空、汽车领域。在船舶领域,张少雄[1]等使用惯性释放功能对某油船舱段结构进行强度计算,消除了边界条件对应力计算结果的影响;赵振宇[2]等应用惯性释放功能对某浮船坞结构进行强度计算,得到了精度较高的应力响应;在航空领域,路林华[3]等使用惯性释放功能对某无人直升机进行了整机强度和刚度分析;Boni[4]等使用惯性释放方法研究了处于自由飞行中的太阳帆在不同辐射角下的结构行为;在汽车领域,孙辉[5]等使用惯性释放功能对某车架进行了强度分析,得到了较符合实际的车架应力分布;Vdovin[6]等对某车架分别使用惯性释放法和传统约束法进行强度分析,结果表明惯性释放法得到的结果更加真实;Banshan[7]等针对某汽车平衡轴架使用惯性释放和子模型法得到了结构的应力分布,并通过与实际结构的疲劳部位对比证实了该方法的有效性。
以上研究借助国外软件的惯性释放功能,取得了理想的效果。但国内极少有人研究惯性释放算法原理并开发对应的程序。惯性释放算法主要有两个关键点:(1)计算结构体在外载荷作用下产生的加速度aI;(2)计算aI引起的节点惯性载荷fI。ANSYS 帮助文件[8]介绍了aI的计算方法,但可能出于保护商业机密的考虑,对fI并没有具体介绍;国产自主有限元系统SiPESC.FEM 具备惯性释放功能,但开发者路林华[9]也没有给出节点惯性载荷fI的具体算法。
本文根据能量原理,独立推导三维块单元由平移和旋转加速度引起的等效节点惯性力,以该算法为基础编写了惯性释放程序,并通过两个算例验证了算法的精度、可靠性和工程适用性。程序和算例文件,可从http://www.huagongchuanhai.cn/fem/获取。
2 惯性释放原理及实现
假设结构有限元模型由p个块单元、q个节点组成,其惯性释放算法在有限元中的实现步骤如下:
(1)计算结构体在不平衡外载荷下产生的加速度
由文献[8]可知,根据达朗贝尔原理,外载荷和惯性载荷组成平衡方程:

式中:Ft和Fr为质心处所受合外力及合外力矩;
Mt和Mr为有限元模型的平动质量矩阵及转动质量矩阵;
at和ar为结构体在外载荷作用下产生的平移加速度及绕质心的旋转加速度。
根据公式(1),计算出平移加速度at和旋转加速度ar。
(2)根据加速度计算节点惯性载荷
这是惯性释放方法的一大难点,目前国内尚没有学者提供计算单元节点惯性力的具体算法,在国外公开的文献中也查不到。本文根据能量方法推导出等效节点惯性力,分别考虑了平移加速度和旋转加速度引起的等效节点惯性力。
平移加速度等效节点惯性力:
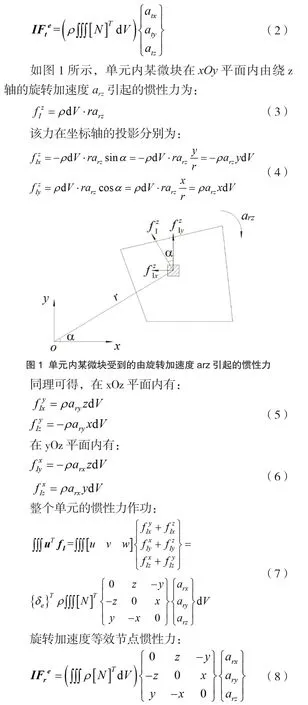
将节点惯性力施加在外载荷向量上,得到新的平衡外载荷向量:

在以上算法的基础上,编写了具有惯性释放功能的三维实体八节点等参单元计算程序,下面通过两个算例来验证其可靠性和工程适用性。
3 算例一
如图2 a)所示:一条长、宽、高分别为L=2 000 mm、B=100 mm、H=120 mm 的 梁,密 度ρ=7.85 e-5 N/mm3,受均布载荷q=30 N/mm,由两端的反力ql维持平衡,求跨中上缘x 方向应力;如图2 b)所示,同样尺寸和材质的梁,去掉跨中载荷,仅保留两端集中力F=ql,在考虑惯性释放的情况下,该问题与图2 a)等效。
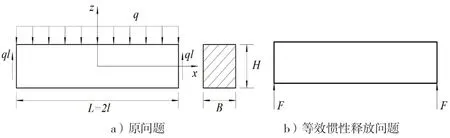
图2 实体梁
3.1 理论解
由弹性力学[10]可知,该梁跨中x 方向应力为:



3.2 有限元解
有限元网格,如图3 所示:对于三维块单元模型,需要对6 个自由度方向的位移进行限制以防止刚体运动。边界条件如下:约束A 点的UX、UY、UZ 自由度,B 点的UY、UZ 自由度;C 点的UY 自由度。需要注意的是,计算完毕后要检查这6 个自由度方向对应的支反力是否为零。如果不为零,则说明边界条件错误,因为它干扰了结构的变形。

图3 实体梁有限元模型及边界条件
设置材料密度后,分别使用本文程序和ANSYS(使用SOLID185 单元)进行了惯性释放计算,计算结果如图4所示。本文程序的积分方式采用6×6×6高斯积分,ANSYS 的单元技术采用默认的全积分法。
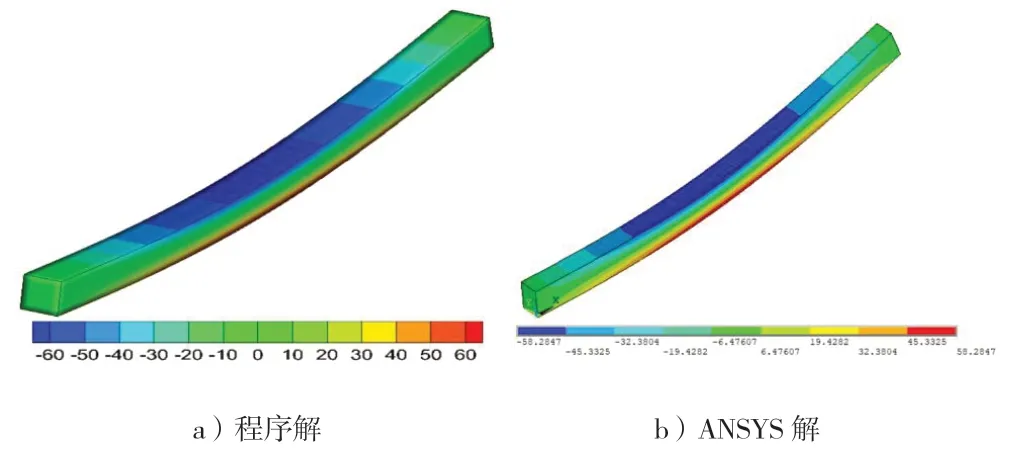
图4 实体梁x 方向应力云图
3.3 结果对比
值得注意的是,在ANSYS 求解中,通过设置不同的KY(2)值将采用不同的单元技术,计算结果也会不同。对比计算结果,如表1 所示。

表1 实体梁算例结果对比
4 算例二
本算例以某钢管(取自某导管架平台组装件)为对象,分别采用本文程序和ANSYS 对钢管吊装过程进行惯性释放计算,并对比计算结果。
4.1 有限元模型建立
钢管结构参数见表2,有限元模型见图5。通过约束A 点的UX、UY、UZ 自由度,B 点的UY、UZ 自由度,C 点的UY 自由度,限制钢管的刚体运动。

图5 导管架平台组装件——钢管

表2 钢管参数
4.2 载荷施加
将起吊力以集中力的形式施加在吊绳与钢管接触的半圆柱面节点上,如图6 a)所示:起吊时采用两条吊绳,分别安装在距离钢管两端500 mm 处;吊绳选取直径为80 mm 的钢丝绳,起吊后钢丝绳与钢管的接触宽度为钢丝绳直径的一半,即接触宽度w=40 mm。

图6 吊装力载荷模拟
如图6 b)所示,吊绳与半径为r 的圆柱接触处单位长度所受法向支持力[11]:

假设沿圆周每隔dθ布置一个节点,沿接触宽度方向布置m个节点,则接触区域每个节点受指向圆心的法向力:

将法向力分解为竖直向上和水平向内的集中力:

将F1和F2施加到接触区域的节点上,如图7 所示。

图7 钢管起吊载荷
4.3 结果评估
约束点的反力为零,可以作为惯性释放解有效性的判别准则[12]。程序计算完成后,首先检查程序输出的节点支反力文件,获得约束节点的支反力均为零,表明边界条件对结构变形并没有影响。
使用可视化后处理软件Tecplot 打开程序计算输出的节点应力和位移文本,可获得钢管的VonMises 应力云图及变形图,如图8 所示:采用惯性释放计算后得到的结构变形是相对于约束节点的,可以看出主要变形部位位于接触区域,应力也集中在吊绳与钢管接触区域,尤其在接触区域底部的钢管内侧应力达到最大;在约束点处没有出现类似支座附近的应力集中、变形失真等异常情况,比较合理地反映了钢管在起吊过程中的应力分布规律。
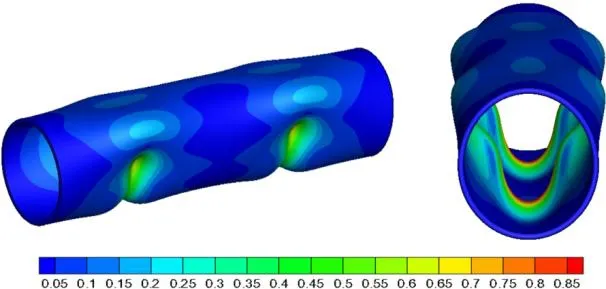
图8 钢管VonMises 应力云图及变形图(程序解)
采用相同的数据模型,使用ANSYS 进行了同样的计算(单元技术采用默认的全积分法),结果如图9所示。
对比图8 和图9 可以发现:程序与ANSYS 计算结果的应力和变形分布一致,二者的最大应力略有差别,程序最大应力为0.866 0 Mpa,ANSYS最大应力为0.937 9 Mpa,相对偏差为7.67%。

图9 钢管VonMises 应力云图及变形图(ANSYS 解)
5 结论
本文在国内首次提出了三维块单元节点惯性力的计算方法,在此基础上编制了相应程序,并通过两个算例进行对比验证,结论如下:
(1)理论算例证明本文提出的三维块单元节点惯性载荷计算方法是可靠的;
(2)约束节点的支反力为零,验证了本文提出的惯性力计算方法能够消除边界节点对变形的干扰;
(3)本文算法获得了符合实际的应力分布,合理地反映了钢管在起吊过程中的应力分布规律:主要变形和应力集中在吊绳与钢管接触区域;约束节点处没有出现应力集中、变形失真等异常情况;计算结果与ANSYS 相当,验证了本文算法的工程适用性。
本文从算法设计到程序实现乃至工程应用,既参考了国外软件和国内外同行的成果,也独立研究了核心算法。文中提出的惯性力计算方法除了三维块单元,还可扩展到平面应力单元、梁单元、薄板弯曲单元等,对国产有限元的自主开发具有一定的借鉴意义。

