考虑闲置产能分享参与者利益的平台定价研究
郝家芹, 赵道致, 韩红帅
(1.宿州学院 数学与统计学院,安徽 宿州 234000; 2.天津大学 管理与经济学部,天津 300072; 3.齐鲁工业大学(山东省科学院)管理学院,山东 济南 250301)
0 引言
在传统经济的生产活动中,闲置产能使用权的分享就已存在,但仅限于“熟人”间的分享,并未成为普遍的资源配置方式,究其原因是产能供给者和需求者之间不能便捷地获取对方的信息。直到互联网、物联网、大数据等信息技术的发展,产能分享平台将市场上海量、分散且未被充分利用的产能信息进行整合,促使产能供给者和需求者能够便捷地获取产能信息,加快了产能使用权分享的步伐,实现了产能使用权在任何经济主体之间的分享和被分享,使得闲置产能使用权的分享成为重要的资源配置方式。
文中产能分享指:以互联网平台为基础,以闲置产能使用权分享为特征,围绕生产各环节,运用分享理念,整合分散、闲置的生产资源和能力,弹性匹配、动态分享给需求者且最大化提升生产效率的新型经济模式。发展产能分享,有利于优化资源配置,提高产能利用率,减少产能闲置。2019年我国产能分享市场交易规模约为9205亿元,比2018年增长11.8%;而2018年产能分享市场规模比上年增长97.5%,增幅出现显著放缓[1]。
《关于深化制造业与互联网融合发展的指导意见》[2]指出,要“推动中小企业制造资源与互联网平台全面对接,实现制造能力的在线发布、协同和交易”。众创型产能分享成为大型骨干企业创新发展的重要方向,服务型产能分享成为生产性服务新模式(如:沈阳机床集团推出的i5智能分享机床等)[3],而中介型产能分享开启了“无工厂”的制造模式(如:淘工厂等)。我国在机械加工、电子制造、工业设计、物流仓储等领域涌现出一批典型的分享制造平台,形成了产能对接、协同生产、分享工厂等多种新模式新业态,显示出巨大的发展潜力。平台在产能分享过程中起着重要的作用,而制定合理的服务收费以吸引更多的用户加入平台,是平台持续经营和发展的关键。
学者们对平台定价问题展开了深入的研究。L'Ecuyer和Maillé[4]利用双边市场理论分析了平台的盈利模式及竞争性平台的相关问题;卢珂等[5]探讨了网约车平台的市场定价问题;Rochet和Tirole[6]从会员费和使用费两个角度研究了垄断性平台和竞争性平台的定价问题;Jia[7]研究了销售平台的收费策略;李静和张玉林[8]探讨了网络效应和业务拓展的平台定价问题;Kung和Zhong[9]研究了配送平台的最优价格策略,比较了会员费、交易费和交叉补贴三种不同策略;Taylor[10]和Bai[11]利用排队论方法研究了按需服务双边分享平台的定价问题;汪旭晖和陈鑫[12]研究了双寡头竞争市场环境下,平台型电商企业、竞争对手和消费者三个经济主体相互作用下的预售定价决策问题;Benjaafar等[13]建立了产品分享模型并比较了利润最大化和社会福利最大化平台的均衡结果;王娜[14]构建了平台型企业的定价模型,运用实际运营数据进行实证检验。
随着产能分享的发展,越来越多的学者开始关注平台参与下的产能分享问题。蔡丹旦[15]提出了众创型、中介型、协同型和服务型四种产能分享平台的运营模式。黄碧丹[16]对石狮服务产业建立的众创型、服务型和中介型这三种产能分享平台的模型进行了分析。王尧和黄官伟[17]探讨了制造业产能分享平台对中小微企业产生的影响。
也有一些学者探讨了不同情形下参与产能分享的企业是否与平台合作及合作模式的问题。Li等[18]探讨了原始设备供应商与第三方平台的合作模式。Ren等[19]在产品回收和不回收两种情况下,分析了产能分享平台的最优定价和服务水平决策,讨论了制造商是否应该与平台合作的问题。Zhang等[20]探讨了制造商进行产能分享时选择自建平台还是加入第三方平台的问题。
上述关于平台定价和产能分享的文献为探究闲置产能分享平台的定价问题提供了理论依据,但并未涉及闲置产能的分享问题,也未针对平台在定价的同时考虑其他参与者的利益问题进行研究。鉴于已有文献存在的不足,本文在已有相关研究的基础上,在平台向供给者收取交易费而对需求者免费的条件下,首先,分别分析利润最大化平台和社会福利最大化平台的定价策略;其次,对这两类平台的定价策略进行分析和对比;然后,探讨以一定权重考虑自身利润的平台X的定价策略,并从理论上分析权重对最优交易费、供给者和需求者的数量以及平台最优利润的影响;最后,通过数值例子验证权重对最优交易费、供给者和需求者的数量以及平台最优利润以及供需双方效用的影响,为平台的定价策略提供理论参考依据。
1 假设与符号说明
本文的假设条件如下:
(1)参与者:垄断的中介型产能分享平台(简称平台)、闲置产能供给者(简称供给者)和产能需求者(简称需求者),他们均具有完全理性;
(2)平台是双边市场且具有正的交叉网络外部性:平台服务的双边用户分别为供给者和需求者,当平台一边的用户越多,另一边获得的效用越大;
(3)供给者和需求者的数量分别为nS和nD。不失一般性,将市场中存在的潜在用户总量均设定为单位1,则供给者的数量nS∈(0,1)和需求者数量nD∈(0,1)分别反应了供给者和需求者在该平台上找到理想交易对象的概率;
(4)供给者和需求者均是异质的:产能闲置给不同的供给者带来的效用vS不同,不同的需求者从传统市场获得产能的效用vD也不同;假设,vS和vD在[0,1]上均服从均匀分布;
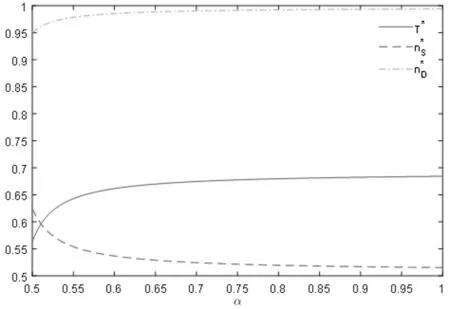
(5)需求者通过网络外部性获得的边际效用小于服务的价格,即λD (6)本文的两阶段博弈模型:第一阶段,平台决策向供给者收取的交易费。供需双方每完成一笔交易,平台仅向供给者收取一定的交易费,对需求者不收取任何费用。第二阶段,潜在的供给者和需求者根据自身效用,选择是否加入平台交易。 文中参数和符号说明如表1所示: 表1 参数及符号说明 本文以垄断的中介型平台为研究对象,探讨仅向供给者收取交易费且考虑供给者和需求者利益的平台的定价问题。垄断的中介型平台,即市场上唯一的平台且本身不拥有制造资源,仅作为第三方对供给者的闲置产能进行整合和匹配,并制定服务价格。 供给者和需求者既可以通过平台进行产能使用权分享,又可以通过其他方式进行产能产权的交易。如果供给者不使用平台,则其所拥有的产能就会被闲置,此时闲置产能将产生一定的费用;如果需求者不使用平台,则其可以通过传统市场购买产能的产权,以满足自身对产能的需求。因此,产能闲置和通过传统市场购买产能分别是产能供给者和需求者的外部选择。 nS=(λS+p-T)nD+cS (1) nD=(λD-p)nS+v+cD (2) 由(1)式和(2)式可知,供给者和需求者的数量分别为: 其中,φS=cS+(v+cD)(λS+p),φD=v+cD-cS(p-λD),kS=λS+P,kD=p-λD,μ=1+(λS+p)(p-λD)。 由于平台上供需双方每达成一笔交易,平台会向供给者收取一笔固定的费用T;供给者的数量nS和需求者数量nD分别反应了供给者和需求者在该平台上找到理想交易对象的概率。不失一般性,令平台上供需双方是一对一的交易,此时完成的总交易量为nSnD。因此,平台的利润函数为: 由供给者和需求者通过平台获得的效用US和UD可知,闲置产能分享给供给双方带来的总效用分别为: 本节首先求解利润最大化的平台收取的交易费,然后求解社会福利最大化的平台收取的交易费,接着分析并对比两类运营模式的平台收取的交易费以及对产能分享参与者的效用产生的影响。 本小节分析利润最大化的平台(记为“商业平台”)向供给者收取交易费的情形。商业平台的本质是逐利的,其以利润最大化为目标向供给者收取交易费。因此,本小节的目标函数为: maxΠP(T)=max(TnSnD) 由一阶必要条件,可得如下定理: 在一些政策条件下,平台可能会选择将社会福利最大化作为目标选择定价策略。本小节分析社会福利最大化的平台(记为“公益平台”)向供给者收取交易费的情形。公益平台通过适当的利益分配机制来最大化社会福利(包括自身利润、供给者和需求者的效用),这类平台往往由政府或公益性组织搭建和运营。 公益平台是以社会福利最大化为目标。因此,社会总福利=平台的利润+供给者的效用+需求者的效用,其函数表达式为: SW(T)=ΠP+SWS+SWD 本小节的目标函数为: maxSW(T)=max(ΠP+SWS+SWD) 由一阶必要条件,可得如下定理: 定理2(1)公益平台向供给者收取的最优交易费为: (2)供给者和需求者的数量分别为: 本小节分析并对比两类运营模式的平台收取的交易费、供给者和需求者数量以及平台的最优利润。供给者和需求者数量函数分别对交易费求一阶导数: 可得如下定理: 定理3(1)供给者的数量随着交易费的增加而减小;(2)需求者的数量随着交易费的增加而增加。 定理3说明:交易费的增加会降低供给者参与产能分享的积极性,导致供给者数量的减少;交易费的增加使得更多的需求者(免费方)愿意通过平台获得所需的产能。 由上述分析,可得: T*1-T*2=[μ(v+cD)+(φD-φSkD)]× [φD(kS-kD)-kDμv]÷ [kDφD+μkD(v+cD)]÷ [(v+cD(kS-kD)+vkD)]≥0 由上述分析,可得如下定理: 定理4(1)商业平台收取的最优交易费和获得的最优利润均高于公益平台;(2)商业平台吸引更多的需求者通过平台获得所需的产能;而公益平台则吸引更多的供给者通过平台进行闲置产能使用权的分享。 定理4说明:(1)商业平台收取的最优交易费高于公益平台,提高了自身的利润,但损害了被收费方(供给者)的利益;(2)商业平台可以吸引更多的免费方(需求者),而公益平台则吸引更多的供给者。 由第3节分析可知,以自身利润最大化为目标的商业平台收取的最优交易费高于以社会福利最大化为目标的公益平台。完全以社会福利最大化为目标的平台可能只是政府为运营主体,而逐利的企业为运营主体的平台则不会以社会福利最大化为目标;但实践中,政府极少搭建平台,而平台的运营主体往往是企业,并且企业在追求自身利润的同时也会承担一定的社会责任,即考虑其他参与者的利益。 为了使平台定价更贴近实际,本小节分析以一定权重考虑其他参与者利益的平台(记为“平台X”)收取交易费的定价问题。假设平台X分别以权重α(1/2≤α≤1)和1-α考虑自身利润及其他参与者的效用。 平台X的效用=α*平台的利润+(1-α)*(供给者的效用+需求者的效用),其函数表达式为: SWT(T)=αΠp+(1-α)(SWS+SWD) =[(2α-1)T+(1-α)(λS+λD)]× 由上式可以看出:当权重α=1时,平台X是商业性平台;当α=1/2时,平台的利润和其他参与者的效用所占的比重相同,虽然此时平台X效用的取值是社会福利的一半,但对平台和供需双方的影响与公益性平台一致,此时的平台X可以看作公益性平台;且α的取值越大说明平台越关注自身利润。 平台X以一定的权重考虑自身利润和其他参与者的效用,其目标函数为: maxSWT(T)=max[αΠP+(1-α)(SWS+SWD)] 由一阶必要条件,可得如下定理: 定理5(1)平台X向供给者收取的最优交易费为: T*={(2α-1)μφS+(1-α)[(kDφS-φD)× (kS-kD)+vkDμ]}÷ {(2α-1)[φD+μ(v+cD)]+ (1-α)kD[(v+cD)(kS-kD)+vkD]} (2)供给者和需求者的数量分别为 {2[(2α-1)μ+(1-α)kD(kS-kD)]} (1-α)kD[(v+cD)(kS-kD)+vkD]}÷ {2[(2α-1)μ+(1-α)kD(kS-kD)]} {(2α-1)[φD+μ(v+cD)]+ (1-α)kD[(v+cD(kS-kD)+vkD]}2 定理6当平台X以一定权重考虑其他参与者利益时,(1)平台X向供给者收取的最优交易费T*随着权重α的增大而增大;(2)供给者的数量随着权重α的增大而减小;(3)需求者的数量随着权重α的增大而增大。 定理6说明:平台利润的权重越大,其向供给者收取的交易费越高,导致供给者(被收费方)的数量减少,而需求方(免费方)数量的增加,即当平台定价时越关注自身利润,向供给者收取的交易费就越高。 上述理论结果为平台定价提供一定的理论指导:(1)平台可以根据供给者和需求者的数量选择适当的权重制定定价策略,以促进闲置产能分享市场的健康发展;(2)政府部门可以对平台进行补贴,以促进平台在定价时尽可能考虑其他参与者的利益。 本节利用数值例子分析权重α取值的变化对最优交易费、参与者的数量、平台的最优利润以及参与者的效用产生的影响。 设p=0.6、λS=0.2、λD=0.2、v=0.7、cS=0.4、cD=0.5,利用MATLAB软件做权重取值的变化对最优交易费、平台的最优利润、供给者与需求者的数量和效用的变化趋势图,如图1和图2所示。 由图1和图2可以得出如下结论: (1)由图1可以看出:随着权重的增加,平台收取的交易费增大,供给者的数量减少,需求者的数量增加。从而验证了定理6; (2)由图2可以看出:平台的最优利润和需求者的效用均随着权重α的增加而增加,但供给者的效用随着权重α的增加而减少;从而说明,增加权重α可以提高需求者通过平台获得产能的积极性,但对供给者产生了消极影响。因此,平台在考虑其他参与者利益时,应根据双边用户的具体情况选择合适权重,以促使产能分享市场向着稳定且健康的方向发展。 图1 α对最优交易费和参与者数量的影响 图2 α对平台最优利润和参与者效用的影响 本文在平台向供给者收取交易费而对需求者免费的条件下,分别构建了利润最大化和社会福利最大化条件下平台定价的模型,分析并对比这两类平台的最优定价问题;然后在上述模型的基础之上构建了以一定权重考虑其他参与者利益的平台X的定价模型,探讨了权重对最优交易费、供需双方的数量以及平台最优利润的影响;最后,用数值例子验证文中重要定理和权重对供需双方效用产生的影响。 研究结果表明:(1)商业平台收取的最优交易费和获得最优利润均高于公益平台;(2)考虑其他参与者利益的平台X收取的最优交易费和最优利润、需求者的数量和效用均随着权重的增加而增加,但供给者的数量及其效用则随着权重的增加而减少。 本文研究了闲置产能分享下平台的交易费定价策略,为平台制定合理的交易费定价策略提供理论参考;文中考虑了平台在制定向供给者收取交易费时兼顾供给者和需求者的利益,使得本文更具有现实意义。本文分析了以一定权重考虑自身利润的垄断中介型平台的最优定价问题,忽略了闲置产能分享市场中存在多个平台而且这些平台直接存在竞争问题,未考虑政府在闲置分享市场中起到的作用,而且也没有考虑闲置产能的价值随时间变化的情形,在未来的研究中可以对这些影响因素做进一步探究。
2 问题描述


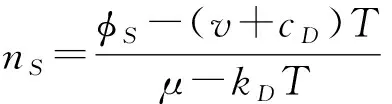
3 基础模型构建及分析
3.1 商业平台的交易费定价分析

3.2 公益平台的交易费定价分析
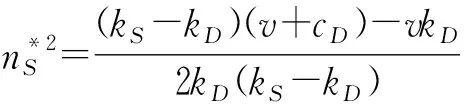
3.3 基础模型的分析
4 平台X的交易费定价分析
4.1 平台X的交易费定价
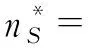

4.2 模型分析
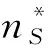


5 数值例子

6 结论

