威布尔更新函数的一个精确近似式
蒋仁言, 张碧雯
(长沙理工大学 汽车与机械工程学院,湖南 长沙 410114)
0 引言
威布尔分布是建模非负、连续随机变量使用最广泛的分布模型[1];威布尔分布的更新函数(简称威布尔更新函数)在可靠性和可用度分析、维修决策优化、质保费用分析、备件库存管理、排队系统、交通流分析等领域有广泛的应用[2~8]。威布尔更新函数没有解析表达式,这给解各种涉及更新函数的优化问题带来极大不便。因此,开发威布尔更新函数的近似式已经吸引了持续的注意。
根据近似式在时间轴t的适用范围,可将各种威布尔更新函数的近似式分为以下两大类。第一类近似式适合于中偏小的t值[9],另一类近似式适合于整个t值范围(即0到∞)。本文着重讨论第二类近似式。
根据模型的构建方式,第二类近似式可进一步分为三个子类:分段函数近似[10~13],级数近似[14~16]和混合模型形式的近似[9,17]。一个好的近似式应同时满足精确性和简单性两个要求。分段模型在结构上简单,但其精度通常偏低。对于某些分布函数(如正态分布和伽玛分布),级数模型的精度随项数的增加而增大,但过多的项数导致近似更复杂[18]。混合形式的近似采用一个权函数将两个极限关系平滑地连接成一个函数;在结构上相对地简单,且其精度比分段函数近似要高,即此类近似能较好地满足精确性和简单性要求。但是,现有混合形式的近似当威布尔形状参数较大时,其精度仍有一定的改进空间[17]。
为了改进现有近似式在形状参数较大时精度欠高的问题,本文提出一个新的混合形式的威布尔更新函数近似式,可供威布尔形状参数是大的(>3.65)情况时使用。此外,通过对比现有各近似式在不同形状参数取值范围内的精度,识别好的近似式,确定其适用范围,从而确立一个基于形状参数的近似式选择方法。
本文结构如下。第1节介绍现有威布尔更新函数的近似式,分析其精度和适用范围。第2节提出新的近似式,分析其精度和适用范围。第3节通过一个维修政策优化的数例例证提出的近似式的精确性和有用性。第4节总结全文。
1 现有近似式及其精度
1.1 更新函数精确值的计算
计算更新函数精确值是评价一个近似式精确性的先决条件。令F(t)记非负随机变量T的分布函数。本文着重考虑F(t)是威布尔分布的情况,其表达式为:
F(t)=1-exp[-(t/η)β]
(1)
这里,β是形状参数,η是尺度参数。在可靠性和维修应用领域,β一般大于1,且很少超过4[12]。平均(μ)、标准偏差(σ)和变异系数(cv)分别为
μ=ηΓ(1+1/β),
σ=η[Γ(1+2/β)-Γ2(1+1/β)]0.5,cv=σ/μ
(2)
这里Γ(.)是伽玛函数。
令F(k)(t)记F(t)的k重卷积(F(1)(t)=F(t)),N(t)记时间区间(0,t]内的更新事件数。更新函数(记为M(t))是离散随机变量N(t)的数学期望,可表达为下面的级数形式或积分形式[15,19]:
(3)
对于大多数分布函数,包括威布尔分布,上述的卷积和积分没有解析表达式。因此,开发更新函数的近似式成为一个重要的研究方向。最简单、最著名的两个近似关系为:
(4)
前者适合小t的情况,后者适合于大t的情况。
对于一个给定的近似式(记为M∞(t)),一个重要的问题是确定它在时间轴t上的适用范围。这个问题等价于评价近似式的精度。为此,需要知道一些β和t的组合下的更新函数的精确值。对于一个给定的β和t的组合,其精确值可通过数值积分法解式(3)中的积分方程获得[20,21]。文献[17]的补充材料(Supplementary Material)显示了η=1,β=1.0(0.5)4.5 (即从1.0到4.5,步长为0.5)和t=0.05(0.05)3.00(即从0.05到3.00,步长为0.05)条件下的威布尔更新函数精确值。这样,近似式Ma(t)的精确性可由下式评价:
ε(t;β)=|1-Ma(t;β)/M(t;β)|
(5)
对于一个给定的β,令εM记上述时间范围内ε(t;β)值中的最大值,用它作为评价近似式精确性的测度。
方程(4)的第一个关系的适用范围可定义为(0,τ1)[17],其中
τ1=sup{t;ε(t;β)<0.01}
(6)
方程(4)的第二个关系的适用范围可定义为(τ2,∞ )[17],其中
τ2=inf{t:ε(t;β)≤0.01}
(7)
这样,“小的t”意味着t<τ1;“中等大小的t”意味着τ1

表1 近似式的εM值
1.2 现有近似式及其精度
以下主要介绍分段形式和混合形式的近似式;级数形式的近似式因缺乏简单性不作介绍。
最早的分段形式的近似式可追溯到Spearman[10],其表达式为
Ma(t)=max[F(t),M2(t)]
(8)

(9)
对于威布尔分布,F(t)和M2(t)有一个唯一的交点[12]。因此,式(8)实际上是一个两重分段模型。表1第2列显示了式(8)的εM值。从中可以看出,该近似的精度偏低。
Parsa和Jin[13]提出一个可积的三重分段线性近似:
(10)

最近,Jiang[11]提出下面的两重分段近似式
(11)
其中,ts是分界点,根据该点处的连续和平滑条件予以确定
M1(t)=H(t)/[1+αH(t)],α≥0
(12)
H(t)是累积风险函数,α是ts的一个已知函数。表1第4列给出了这个近似式的εM值。从中可以看出,这个近似式比前述两个近似式更简单、更精确。但是,随着β的增大,εM值快速增大。
Jiang[12]修改式(12)为
M1(t)-F(t)/[1-αF(t)],α≥0
(13)
分界点ts以类似的方式确定,α是ts的已知函数。表1第5列给出了该近似式的εM值。从中可以看出,当β较大时,该近似式比由式(11)和(12)所构成的近似式更精确。然而,当β较大时,εM值仍然偏大。
Jiang和Chen[17]提出下面的混合形式的近似式:
Ma(t)=w(t)M1(t)+[1-w(t)]M∞(t)
(14)
`其中,由下式确定[9]:
M1(t)=pF(t)+(1-p)H(t)
p=1-exp{-{(β-1)/0.873}0.9269}
(15)
权函数是β的函数:
w(t)=1-Φ(t;μw,σw)
(16)
这里,Φ(t;μw,σw)是参数为μw和σw的正态分布函数,μw=(0.9139+0.2020β)η,σw=(|0.6302β-2.0001|+0.1226)η/6。
2 提出的近似式及其精度
2.1 提出的近似式
提出的近似关系取式(14)的形式,具有不同的M1(t);权函数w(t)有不同的参数。
Baker[22]提到,当t>2μ时,式(4)中的M∞(t)一般地是精确的。这意味,M1(t)应该恰当地确定使其在时间区间(0,2μ)内是精确的。下式可能满足这个要求:
(17)
为简单起见,使用一个分布函数G2(t)近似F(2)(t);使用另一个分布函数G3(t)近似F(3)(t)。这样,M1(t)被定义为
M1(t)=F(t)+G2(t)+G3(t)
(18)
考虑威布尔、伽玛、正态和对数正态分布作为G2(t)和G3(t)的备选模型。对于一个给定的β和η的组合,使用式(2)计算F(t)的均值μ和方差σ2。则F(k)(t)(k=2,3)的平均为kμ,方差为kσ;Gk(t)的参数用矩法确定。例如,如果Gk(t)是形状参数为uk、尺度参数为v的伽玛分布函数,则
uk=kμ2/σ2,v=σ2/μ
(19)

表2 备选模型的εA值
为了对比备选模型的性能,类似于计算威布尔更新函数的精确值,使用数值积分方法计算F(k)(t)的精确值。对于一个给定的备选模型和β值,计算在t/η=0.05(0.05)2.00处的相对误差εg(t),εA令记这些相对误差的平均,用它作为评价备选模型性能的测度。采用相对误差(而非绝对误差)的目的是为了强调备选模型的左尾特征,因为M1(t)适用于中偏小的t值。
表2显示了备选模型的值εA。它清楚地表明,伽玛分布是最好的。因此,G2(t)和G3(t)是伽玛分布,其参数由式(19)计算。现在确定权函数的参数:μw和σw。仔细分析M1(t)和M∞(t)之间的交点发现有以下三种情况:
·对于β=1, 它们相交在原点。
·当β大于且接近于1时,有一个交点(参见图1,ΔM(t)=M1(t)-M∞(t))。
·当β较大时,M1(t)和M∞(t)之间有多个交点(参见图2)。用t1记最小的交点,用t2记最大的交点。在这两点之间,随着t的增大,和越来越接近。

图1 ΔM(t)=M1(t)-M∞(t)的图形(β=1.5)
对于β=1.0(0.5)4.5,表3第2和第3行给出了对应的t1/η和t2/η的值。平均参数μw取t1和t2的加权和,即
μw=w1t1+w2t2
(20)
为使μw更接近于t2,假定wk(k=1,2)正比于tk。这得wk=tk/(t1+t2)。式(20)成为
(21)

表3 t1/η、t2/η、μw/η和σw/η的值
标准偏差参数σw取为
σw=(t2-μw)/Φ-1(0.999;0,1)=(t2-μw)/3.0902
(22)
这里Φ-1(.)是正态分布的逆函数。当t1=0时,μw=t2,取σw=0.01η。表3最后两行给出了μw/η和σw/η的值。
2.2 本文近似的精度
表1倒数第2列给出了本文提出的近似式的εA值;最后一列给出最好的近似式。从中可以看出,在β=1.5和2.0之间,最好的近似式由文献[11]的近似变为文献[17]的近似。使用二次多项式插值法推断两者在β=1.69处有相同的εA值。类似地,在β=3.5和4.0之间,最好的近似式由文献[17]的近似变为本文提出的近似,并且推断两者在β=3.65处有相同的εA值。因此,我们可以得出以下结论:
·对于β<1.69,由Jiang[11]所提出的近似式提供最好的精度;
·对于β=1.69-3.65,由Jiang和Chen[17]所提出的近似式有最高的精度;
·对于β>3.65,本文所提出的近似式是最精确的。
·按照以上β值范围选择模型,最大相对误差将小于2%。这个精度满足一般应用的要求。
3 示例
当一个产品含有几个相同的元件(如轴承),作为一个基于时间的预防维修政策,批更换政策(block replacement policy)可能适用于这些元件的预防更换[23]。在这个政策下,每隔时间周期Tp,元件被预防地更换;如果元件在此之前发生失效,则只更换失效的元件。
在时间区间((k-1)Tp,kTp)(k=1,2,…) 内,每个元件的失效事件形成一个更新过程,平均失效数为更新函数M(t)。令cp记每个元件的平均预防更换费用,cf记失效更换费用。通常,cf比cp大得多。在上述时间区间内的期望费用率为[23]
J(Tp)=[cp+cfM(Tp)]/Tp
(23)
如果采用失效更换政策,费用率将是J(∞)=cf/μ。批更换政策的有效性可用维修费用节省率描述:
(24)
此值越大越好。
设想元件寿命服从β=4.0和平均寿命为700小时的威布尔分布;cf和cp的值分别为100和250费用单位。使用精确的更新函数求得的最优解显示在表4第一列。如果采用失效更换政策,费用率将是0.3571。这表明,批更换政策能带来ηe=21.42%的维修费用节省。因此,对于本文数例,批更换政策的有效性十分明显。

表4 基于不同近似式的最优解和相对误差值
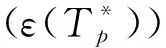
为进一步例证本文所提出的近似式的精确性,表4最后五列显示了从其它五个近似式获得的最优解和相对误差值。从中可以看出,只有从文献[17]的近似式得到的最优解的精度是可以接受的。这例证了基于β值选择近似式的必要性。

表5 本文近似式的参数
3 总结和结论
本文系统地总结了威布尔更新函数的近似计算式,针对现有近似式在β较大时精度不高的问题,提出了一个新的近似式。精度分析发现,当β<1.69时,由Jiang[11]所提出的近似式是最精确的;当β∈[1.69,3.65]时,由Jiang和Chen[17]所提出的近似式是最精确的;当β>3.65时,本文所提出的近似式是最精确的。若按此选择近似式,最大相对误差将小于2%。
本文数例例证了所提出的近似式的精确性,基于β值选择近似式的必要性,以及维修决策优化的有效性。
注意到用伽玛分布G2(t)和G3(t)近似F(2)(t)和F(3)(t)的精度仍有改进的空间(见表2),故寻找更好的分布模型供近似F(2)(t)和F(3)(t)是一个值得进一步研究的课题。

