通信塔桅结构的单点脉动风时程模拟
刘言彬
中国铁塔股份有限公司江苏省分公司
0 引言
通信铁塔是一种高耸结构,高度高、外形细长,阻尼小,对风荷载尤为敏感,风荷载起决定控制作用,其在风荷载作用下塔身振动和侧向位移等动力响应十分显著。从大量实测数据记录和试验结果表明,空间任一点的自然风是由平均风和脉动风组成的,平均风本质是动力的,因其周期远超过一般结构的自振周期,故可等效为静力作用;脉动风往往周期较短,它的强度呈现瞬时随机变化,可近视看作为动力作用。故自然近地风对高耸结构的作用,可看作平均风的静力作用和脉动风的动力作用的叠加。
由于脉动风本质是一种随机动态作用,可以用随机振动理论方法来进行分析研究,一般随机振动通常都具有各向异性、非重现性性质,但还是有一定的统计规律,可以用概率论的方法来统计分析。脉动风速本身可用高斯平稳随机过程(具有零均值特点)来描述,且其具有明显的各态历经性。实际上脉动风是一种三维的风湍流,由顺风向、横风向和垂直向的湍流三部分组成。垂直向、横风向的湍流往往较小,因此实际工程中一般只讨论顺风向的湍流。
目前通信铁塔的设计依据主要有《建筑结构荷载规范》(GB50009-2012)、《高耸结构设计标准》(GB50135-2019)、《移动通信工程钢塔桅结构设计规范》(YDT5131-2019)及《钢结构单管通信塔技术规程》(CECS236:2008)等,这些规范中规定的设计方法均是把风荷载当作静力荷载考虑。然而,通信塔具有柔性强和风敏感的特点,在强风作用下发生强烈振动甚至倒塌破坏也较为常见,因此对结构进行动力响应分析就显得十分重要。
当前5G 建设应充分挖掘已有资源共享潜力,通过共享提升降低5G 项目投资造价、实现行业降本增效。5G 新基建多为非独立组网,一般通过利用原4G 站址升级改造,通过塔身新增抱杆来加挂5G 设备,以加快5G 网络快速部署。但在方案设计、工程实践中,由于存量基站塔身承载能力不足、规范中风荷载计算方法未考虑脉动风的影响,塔身弯曲变形、塔顶晃动现象严重,导致5G 建设进度受阻、安全隐患较大,因风荷载计算问题导致塔身无法直接挂载设备,给5G 工业化应用和网络部署造成了一定的困扰。故对风荷载重新模拟,并与现有规范中风荷载计算方法进行比对,充分使用各类有限元软件进行仿真建模分析,完善存量站址的承重复核计算显得尤为必要。
1 风及风荷载的表达
1.1 风的描述
风是空气相对于地面从高压地区向低压地区的运动形成的。风的时程曲线包括长周期、短周期两个部分,长周期时长一般在10分钟以上,短周期时长通常在几秒至几十秒左右,故在实际应用中常把长周期部分的自然风作为平均风,短周期部分的瞬时风作为脉动风来加以分析。在对自然近地风的分析和研究中,一般是用风速来描述。塔桅结构在任意t 时刻z 高度处的风速,可用平均风速与脉动风速之和来表达。

式中:v(t)为平均风速;vf(z,t)为脉动风速。
平均风速是随高度变化的,而脉动风是瞬时变化的随机变量,它施加给结构的作用是随时间变化的,对结构的疲劳寿命、使用舒适度影响较大,在某些情况下还会引起结构共振,后果严重。由于脉动风速本身具有明显的各态历经性,可用具有零均值的高斯平稳随机过程来描述,并可借助概率论中统计方法进行分析。脉动风具有两个明显的概率特性:脉动风速谱、相干函数。水平脉动风功率谱密度函数是脉动风最重要的统计特征,其反映了某一频率域上脉动风的能量大小。
目前国内外有很多风工程学专家都对水平脉动风功率谱展开了研究并提出了各自的表达式,其中加拿大Davenport 教授提出的脉动风速谱最著名、应用较为广泛。Davenport 根据世界上不同地点、不同高度处测得的多次强风记录展开研究,认为水平脉动风速谱中,紊流尺度沿高度是不变的,可按下式计算:

K 为表面阻力系数,与地表特征有关。
Davenport 认为风速谱是沿高度不变的。鉴于我国现行规范仍一直参考使用Davenport 风速谱,故本文针对风荷载的模拟研究也同样使用了Davenport 风速谱。
1.2 风荷载的表达
在工程结构设计应用中,常把风荷载大小用风压来衡量。直观表述:风压会随着风速的增大而增大,风速风压的关系可由伯努利方程推导得出。
根据空气动力学的研究结果,风速与风压之间存在着一定的数学关系,并且可以将风压分为平均风压和脉动风压:

平均风压取决于平均风速大小,而脉动风压既与脉动风速有关,又与平均风速有关。脉动风压可用统计方法表达,根据脉动风速的风速谱Sv(f),可求得对应脉动风压的功率谱Sw(f)。
2 风荷载的模拟理论
模拟脉动风速时程的方法主要有谐波叠加法、线性滤波法、小波分析及逆傅里叶变化法等。George Deodatis 提出的谐波合成法,对于一维多变量零均值的平稳高斯随机过程向量f(t)={f1(t),f2(t),…,fn(t)},其互功率谱密度矩阵为:
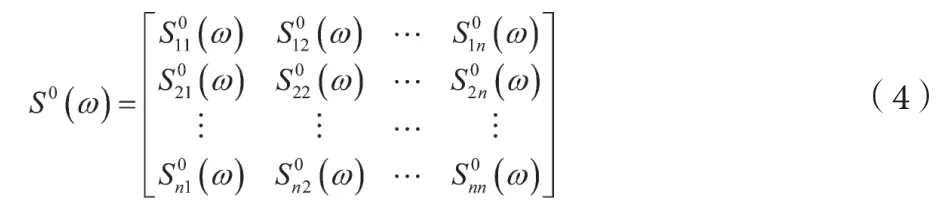
式中,S0jj(ω)为自谱密度函数,S0jm(ω)(j ≠m)为互谱密度函数,j,m=1,2,…,n。互谱密度矩阵进行Cholesky 分解后得:
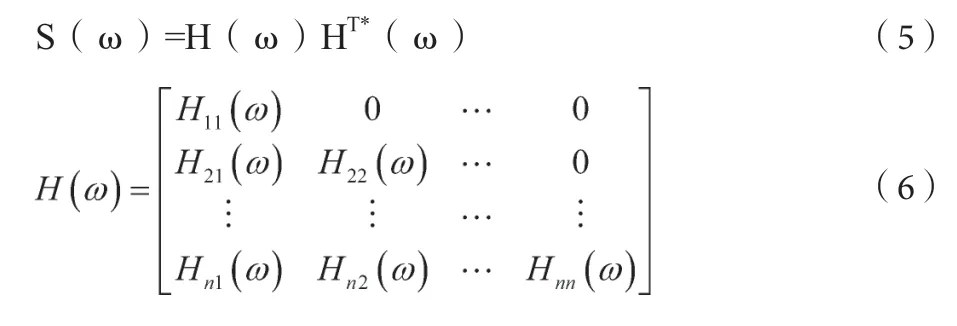
式中,HT*(ω)是H(ω)的共轭转置矩阵。是复矩阵,且对角元素为实数,非对角元素为复数。H(ω)中各元素之间有如下关系:
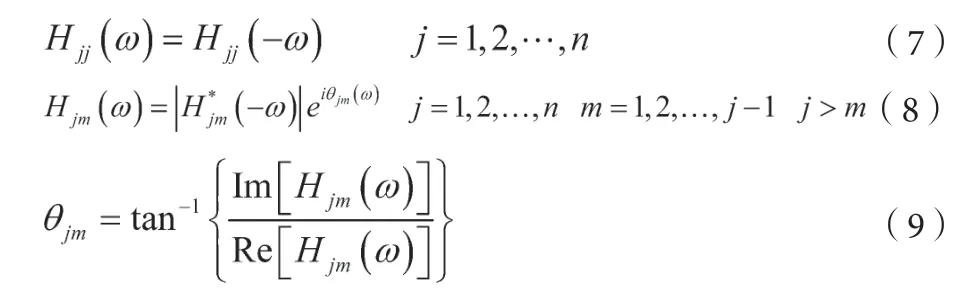
式中,Im 表示取虚部,Re 表示取实部。
根据Shinozuka0和Deodatis0的研究,随机过程{f0j(t)}的样本{fj(t)}也可用如下公式进行模拟:
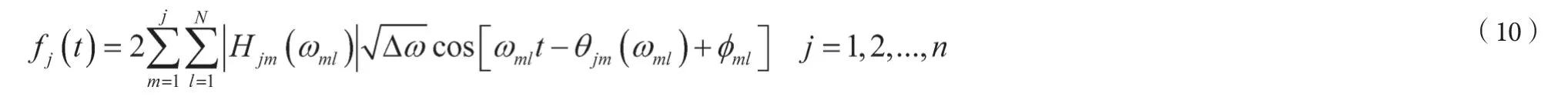
其中,Δω=ωu/N,ωu为截断频率,ωml为双索引频率,φml为随机相位角,其在区间[0,2π]上均匀分布。为了增大模拟样本的周期,双索引频率可按以下公式计算:
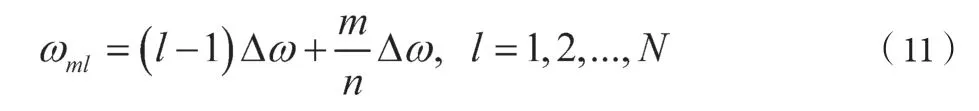
此外,在使用式(10)生成函数样本时以防混叠,时间步长Δt 应满足下列限制条件:

由以上公式模拟的随机过程周期可表述为:

可以发现公式(10)模拟的多变量随机过程样本的总体均值和总体相关函数,均较好的收敛于目标值,且呈现各态历经性。
至此,若已知S0(ω),合理地选择了N,ωup和Δt,则可以获得良好的随机过程样本。
为了减少风场模拟的计算量,可运用FFT 技术,这样就会进一步提高计算效率。与Deodatis0推导过程类似,式(10)亦可改写为如下形式:
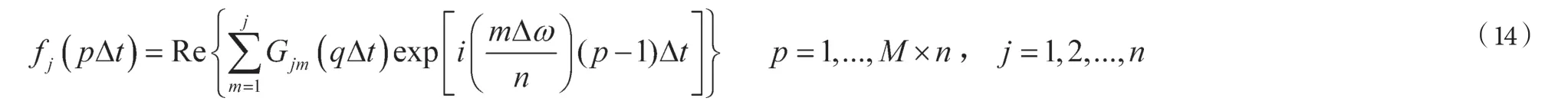
其中,M≥2N,q 是p/M 的余数,q=1,2,…,M。Gjm(qΔt)由下式给出:
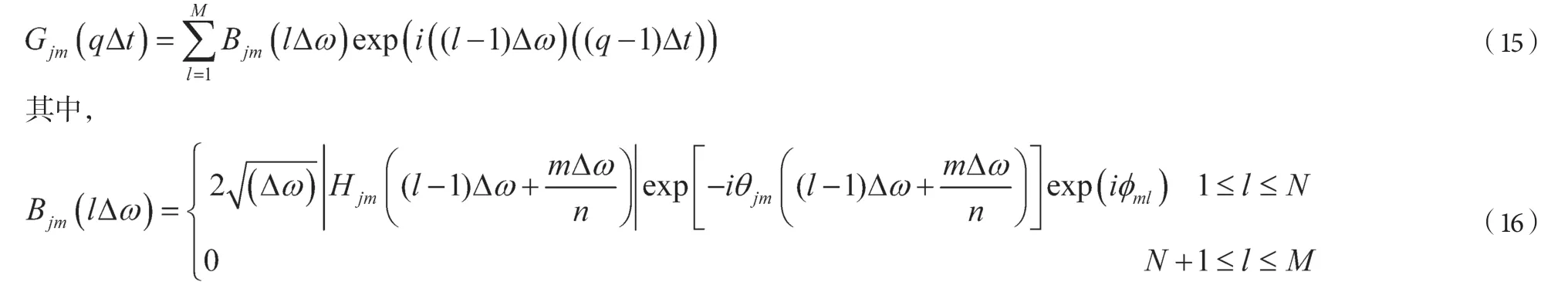
将式(15)改写为:
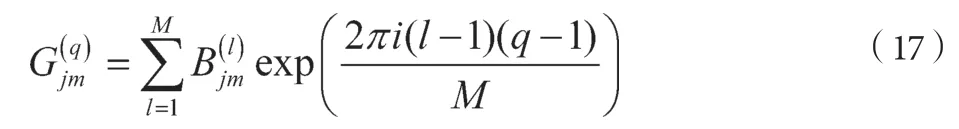
其 中,G(q)jm=Gjm(qΔt),B(l)jm=Bjml(lΔω)。由以上公式可知,G(q)jm即为B(l)jm的离散型傅里叶变换,故可用FFT 计算。此外,根据公式Δt=2π/(MΔω),为了防止频率混叠,要求满足M≥2N 的条件。
3 数值模拟方法
通信铁塔是一种高耸、柔性、风敏感、自振周期较长的结构,在风荷载作用下塔身振动、侧向位移较为明显,风荷载动力响应十分显著。近些年来,铁塔在强风作用下塔身弯曲变形、连续倒塌破坏事故频发发生,严重影响了人民群众的生产生活和经济损失,故应重视通信铁塔结构的抗风设计、整体稳定性。目前,对风荷载作用下结构的动力响应分析研究较少,基于此,本文以某典型通信塔工程风场作为算例,水平脉动风速谱选择Davenport 谱,利用MATLAB 软件编制模拟了单点水平脉动风速曲线的程序,对算例风场进行仿真模拟。风场模拟计算的主要参数见表1。
3.1 工程概况
本工程采用塔高为40 米的低成本单管塔,在标高38.75米(第一层支架)和35.5 米(第而层支架)设置两层支架,一层支架有6 根天线抱杆,每副天线(含RRU)迎风面积不大于0.6m²,二层支架有3 根天线抱杆,每副天线(含RRU)迎风面积不大于0.8m²。本通信铁塔设计基本风压为0.35kN/m²,设计基准期和设计使用年限为50年,地面粗糙类别为B类,结构安全等级为二级,抗震设防类别为丙类。
工程采用同济大学编制的“空间钢结构系统CAD 软件3D3S”有限元软件进行结构建模分析,主杆采用梁单元,爬梯、螺栓、天馈线、RRU 的质量通过简化成集中质量点的方法施加在塔身上,塔底采用固接方式,不考虑土与铁塔结构之间的相互作用,建立铁塔模型并对其进行动力特性分析。本典型工程铁塔实物图、尺寸图及有限元模型,如图1 所示。
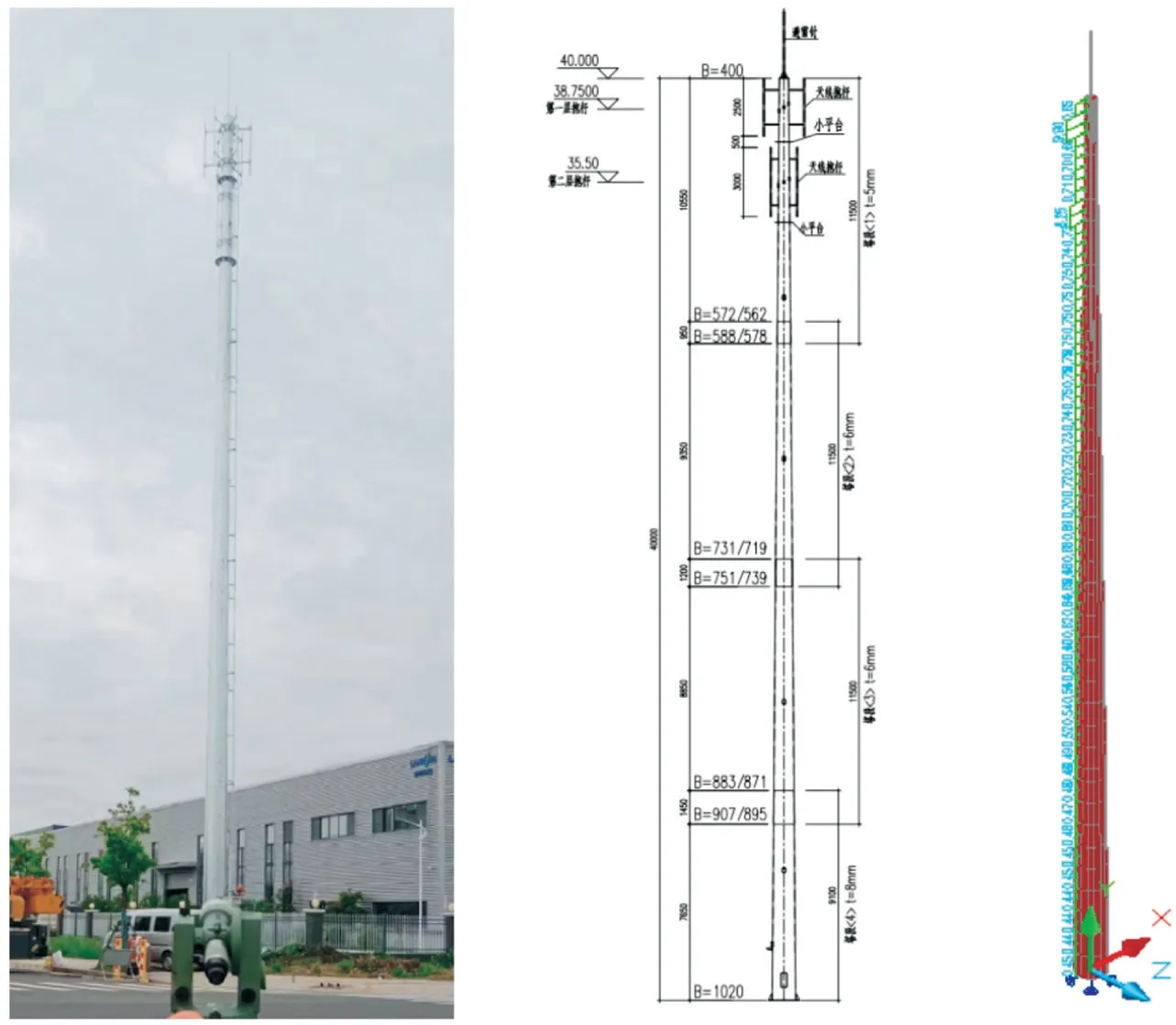
图1 典型工程铁塔实物图、尺寸图及有限元模型
3.2 风荷载模拟
基本风压系以当地比较空旷平坦地面、离地10 米高、统计50 年一遇的10min 平均最大风速为标准。基于上述风荷载模拟方法,对该通信铁塔进行风速模拟,但在实际分析中不可能把塔身每一点的风速时程模拟出来,故参照荷载规范基本风压离地高度选取离地10 米处的塔身单点进行风场模拟。选取平均风速=16m/s,频率范围等分数N=1024,时间步长dt=0.01s,基于谐波叠加法,模拟平均风速10m/s 时该铁塔10 米高度处的风速时程,风场模拟计算主要参数如表1 所示。
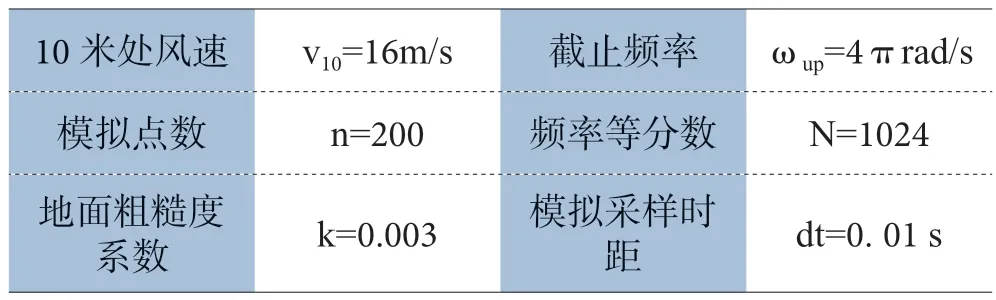
表1 工程结构风场模拟计算主要参数
根据以上参数及模拟理论,以节点作为风荷载作用点,模拟了单点脉动风速时程曲线,并检验了样本的主要统计特征,得出脉动风速时程曲线图如图2 所示,模拟功率谱和目标功率谱关系曲线如图3 所示。
图2 为利用MATLAB 编写程序模拟的风时程曲线片段;把模拟的脉动风速时程转换到频域中,且模拟点处水平脉动风速功率谱密度与目标谱密度的比较见图3,图3 可以看出,在低频部分模拟谱与目标谱有一定误差,因此在前计算应用中,可忽略前若干点,以免除瞬态效应。在其他部分,模拟谱比较接近目标谱。
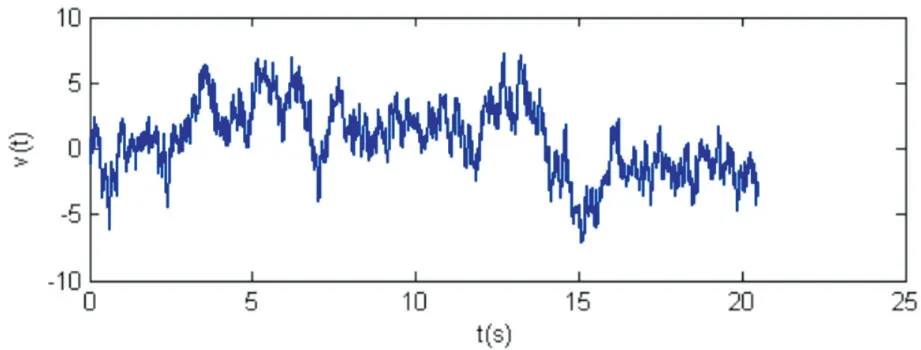
图2 脉动风风速时程曲线
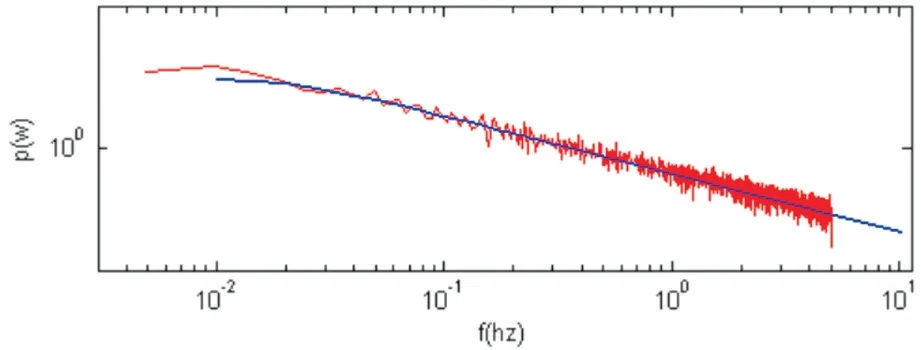
图3 模拟谱和目标谱关系曲线(蓝线:目标谱;红线:模拟谱)
4 结论
(1)上述模拟理论表明样本模拟功率谱与目标功率谱较为吻合,验证了该方法的合理性,可以作为通信铁塔风荷载作用下脉动风的模拟理论。
(2)在谐波合成法模拟风场过程中,应用CHOLESKY 分解互谱密度矩阵和应用FFT(快速傅立叶方法)进行三角函数的叠加都可以提高工作效率,减少计算工作量。
(3)脉动风的模拟可以为研究高耸结构在脉动风荷载作用下的风振响应提供一定的理论依据,从而为以后高耸结构的设计提供一定的参考。
5 结束语
本文首先介绍了风和风荷载、风荷载的模拟理论,结合通信铁塔高耸、轻柔、风敏感等结构特点,以某典型通信铁塔工程为研究对象,水平脉动风速谱选择Davenport 谱,利用MATLAB 软件编制模拟了单点水平脉动风速曲线的程序,对算例风场进行仿真模拟。然后将模型模拟样本的自功率谱与目标功率谱进行比较,吻合结果较好,也验证了该方法的合理性。然而,针对该高耸结构动力响应问题的研究不仅要依赖数值模拟,还需要借助试验研究和实测分析等手段,将三者结果进行对比分析,才能取得更有价值的研究成果。

