开挖基坑土钉内力增量计算方法

赵 喆，马映昌

（1.甘肃省建筑科学研究院（集团）有限公司，甘肃 兰州 730070；2.大连理工大学，辽宁 大连 116024）

1 引言

基坑开挖中土钉构建支护体系得到广泛认可，工程应用已较为成熟，但基坑开挖施工的复杂性和内力计算理论研究的滞后性，导致现行土钉内力计算未形成完备方法。开挖基坑时土压力三角形分布形式因简便合理故普遍采用，但规程计算中直接将土钉内力按土压力三角形面积分配并不符合实际情况，采用该种计算方式引发许多工程事故发生。

《建筑基坑支护技术规程》（JGJ 120—2012）[1]中忽略基坑开挖的施工过程，将开挖产生的土压力一次分配给所有土钉，造成上层土钉内力较小、下层土钉内力较大的不合理分布。杨光华[2-3]在开挖基坑施工中提出增量法计算，分步将施工过程的不平衡土压力进行合理分配，最终叠加求解土钉内力总值，但其文中仅仅叙述计算过程和思路，并未将该方法总结归纳为公式。郭红仙等[4]提出土钉支护基坑中开挖影响面的作用，详细叙述了开挖土压力的概念及形式，采用增量法进行计算并验证。郭院成等[5]表明了增量计算过程中合理分配内力增量可以有效提升计算结果准确性，采用增量法计算在工程中将预应力锚杆和土钉进行合理分布。周勇和胡玉丽[6]基于改进增量法探究桩锚支护位移与内力关系，通过有限元模拟表明基于增量法形成的内力计算的合理性与可靠性。陈俊成和宿文姬[7]分析了多种土压力形式下土钉受力的特征，表明三角形土压力分布形式较其他分布形式与工程监测结果更为接近。

根据以前学者的研究看出采用增量法可以合理计算土钉内力，明确开挖过程中土钉受力和基坑变形状况[8-9]。但随着工程规模的扩大，基坑开挖愈深且土钉布置愈发复杂，不同工况下土钉内力计算愈发繁琐，故通过对基坑开挖步骤的分析，以增量法为基础总结出土钉增量内力计算公式，提出土钉内力增量计算方法，依托MATLAB软件平台进行了程序编制和软件开发。

2 土钉内力增量计算方法及软件开发

2.1 土钉内力计算变化

图1为有无土钉支护的摩尔应力圆[10-11]，对比可知：竖直方向上σ1变化较小，水平方向上σ3明显提高。无支护时强度包络线穿过摩尔应力圆，故无支护基坑开挖时往往易发生破坏。当采用土钉支护时莫尔圆σ3得到提高，表明施加土钉后承载了土体开挖应力，保证了整体结构的安全。基坑施加土钉后形成钉土复合体承载剪应力，也对应着Janbu条分法（极限平衡）模量公式Et=Kpa（σ3/Pa）n中σ3增长使复合体变形模量Et增大，最终表现为有效提升整体抗剪性能。

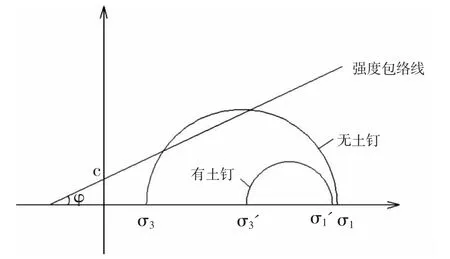
图1 有无土钉支护土体应力摩尔圆

《建筑基坑支护技术规程》（JGJ 120—2012）在基坑开挖过程中土压力采用三角形分布，如图2所示。但如果将土钉支护直接按照面积划分土压力值，土钉承载力又是与长度成正比，故土钉长度应随着开挖深度从上至下逐个增长，但与实际状况并不相符。根据图2最下层土钉力应最大，但实际施工中最下层土钉在基坑开挖至底部且完成变形后施工布置，故最下层土钉应并未受到基坑开挖的增量荷载。由于开挖中土压力三角形分布与各层土钉实际内力分布的差异较大，应基于基坑开挖分步施工的特点对土钉内力采用增量法计算。

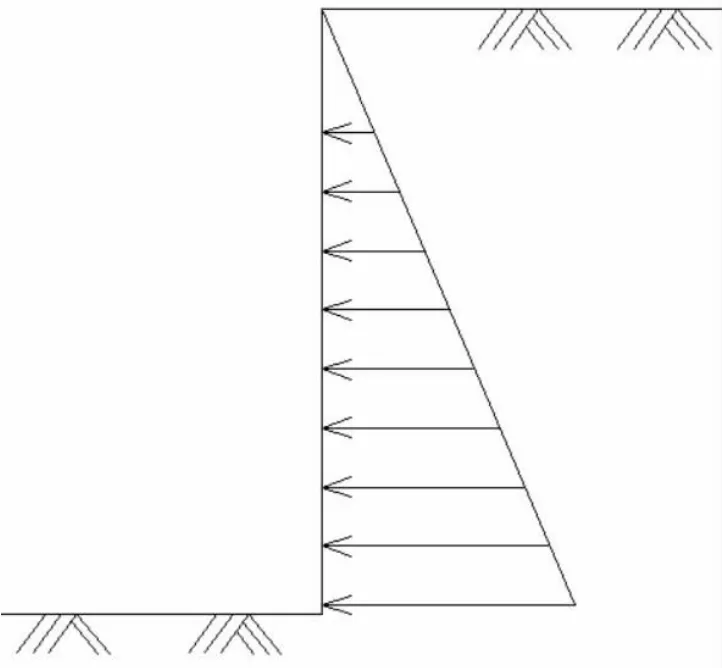
图2 三角形土压力

2.2 土钉内力增量计算

基坑开中计算土钉内力采用荷载增量法，其实质为将整个过程分为多个施工步骤，根据各步骤产生的荷载增量对各层土钉分配内力进行计算，施工完成后对各层土钉所受内力进行叠加，最终求得土钉内力终值[12-13]。

假定基坑分布开挖过程中土钉内力仅分担内力时发生变化且土钉倾角不变，基于荷载增量法对土钉内力变化过程进行分析：图3为基坑开挖示意图，如图3（a）所示，基坑开挖第一层土体时无土钉支护，土体内部变形稳定，施工第一层土钉后土钉无增量内力；如图3（b）所示，开挖第二层土体时增加侧压力△T21由第一层土钉承担，之后施工第二层土钉；如图3（c）所示，开挖第三层土体时产生的侧压力由两层土钉的内力增量共同承担，第一层土钉承担△T31，第二层土钉承担△T32，之后施工第三层土钉；如图3（d）所示，最后一层土体开挖后，不平衡侧压力由上方土钉共同承担，最后施工的最下层土钉不受力。

图3 基坑开挖示意图

根据开挖过程，n层土体开挖完成后各土钉内力分别为：

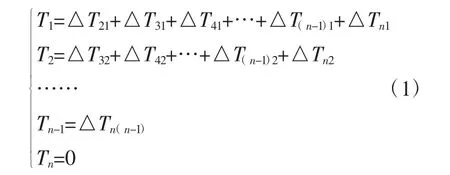
式中：Tn为第n层土钉内力。

由于本研究将各层土体开挖时产生的不平衡侧向土压力均分配于上层土钉，故土钉承担的总量值应等于不平衡土压力总值，但各层土钉的内力增量尚未形成合理分配方法。由于各层土体承担内力与开挖过程中分配的内力增量关系密切，为准确计算工程实际土钉内力，需要形成合理分配方法。根据杨光华等研究成果，土钉刚度和位置采用就近分配原则在基坑开挖时分配各层土钉内力增量。

就近分配原则中土压力分配与土钉刚度、土压力中心位置和土钉位置有关；由于土钉刚度相同，故分配时仅考虑土压力中心位置和土钉位置。图4为各层开挖侧向土压力图。

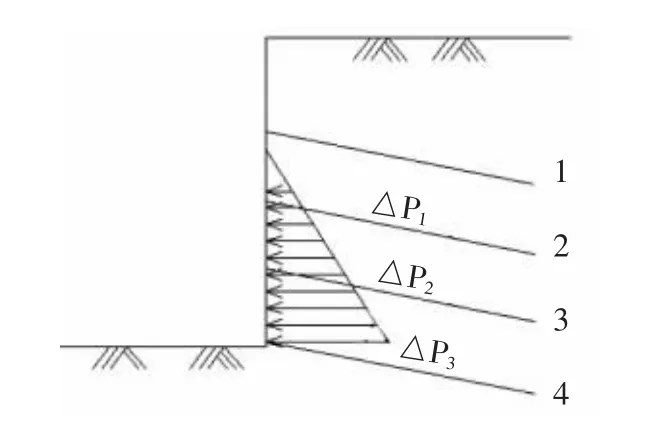
图4 侧向土压力

第一层土方开挖变形完成后第一层土钉施工，无内力增量产生。

第二层土方开挖，此时新增内力△P1由第一层土钉承担，故此时内力增量为：△T21=△P1。

第三层土方开挖，新增内力△P2由第一层土钉和第二层土钉共同承担，根据就近分配原则，△P2中心到第一层土钉的距离为l1，△P2中心到第二层土钉的距离为l2（下同）。第一层土钉分配内力为l2/（l1+l2）·△P2，第二层土钉分配内力为l1/（l1+l2）·△P2。即：

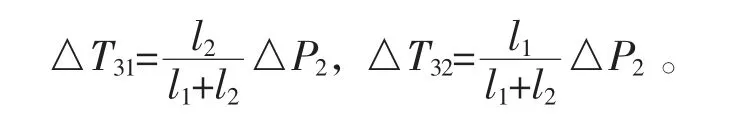
第四层土方开挖，新增内力△P3，按上述分配原则，根据上文计算可知：

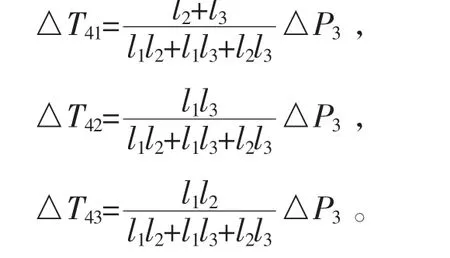
基于上述计算结果，第n层土体开挖，第m层土钉内力增量通用公式为：

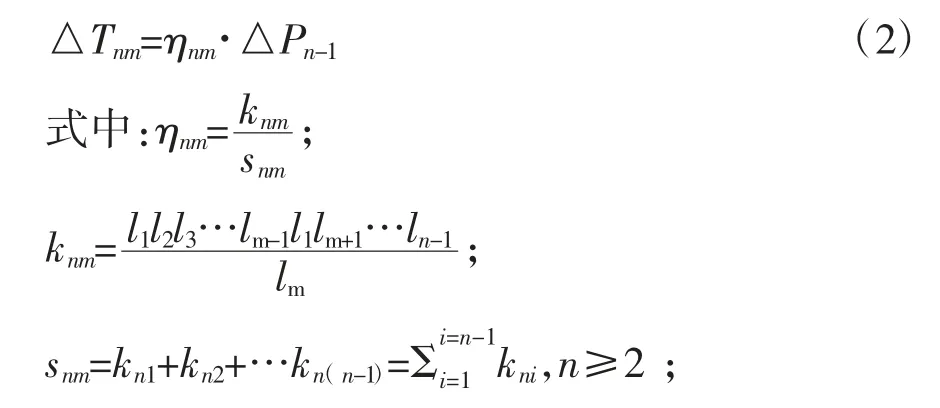
△Pn-1为第n层土体开挖的新增内力；li为△Pn-1中心到第i层土钉的距离。

根据上式，第n层土方开挖，新增内力△Pn-1，则分配给各层土钉内力增量为：

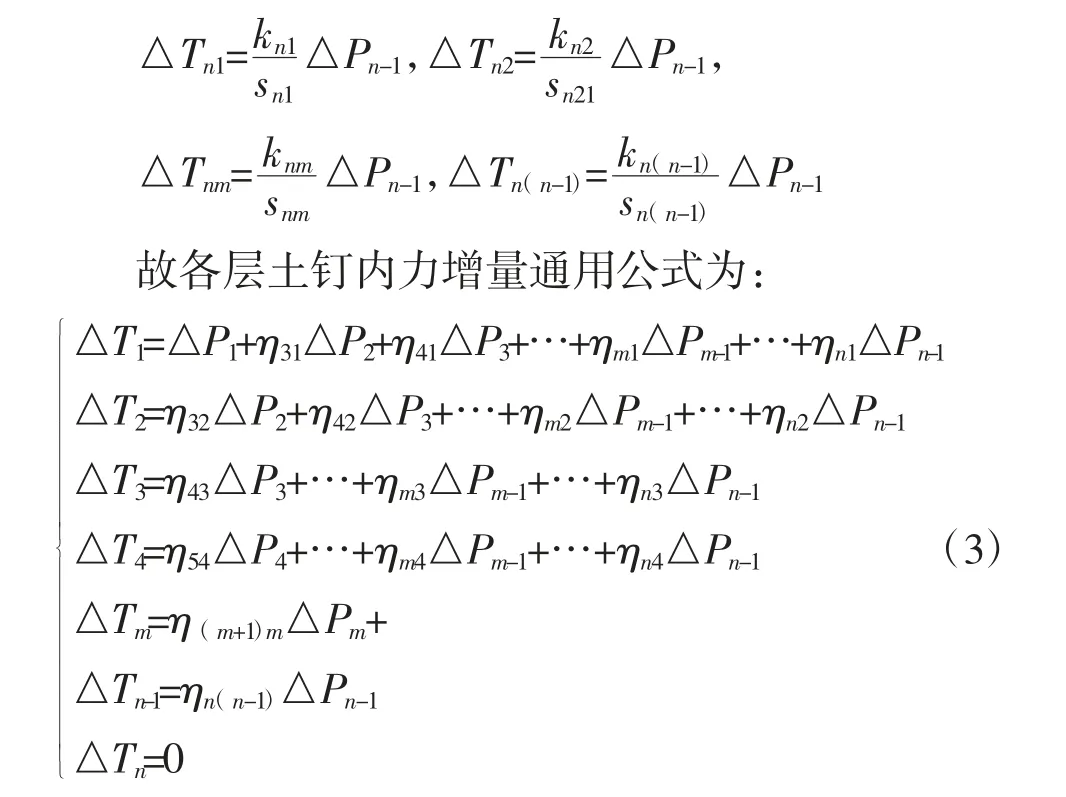
根据就近分配原则及相关假定，在确定基坑开挖层数、土压力中心位置和土钉距离后可开展土钉内力的计算。

2.3 软件开发

上文已给出内力增量计算的关键公式，但由于公式（1）～（3）的结构复杂，实际计算时较为繁琐。为方便该计算方法的使用，减少人工计算的工作量，在确定内力增量计算方法的基础上，依托MATLAB软件编写程序并进行软件开发。该软件主要有参数输入、模型构建、内力公式和结果输出4个部分，输入参数后可快速构建模型，最终输出土钉内力结果。如图5所示，在参数设置页面选择土体不分层后，可进行土体参数和土钉位置参数输入，完成设置后进行模型的构建；当土体分层时需选择土质分层，之后根据分层状况进入多个页面逐个输入分层土体参数。图6为土钉内力公式图，图7为结果输出图。

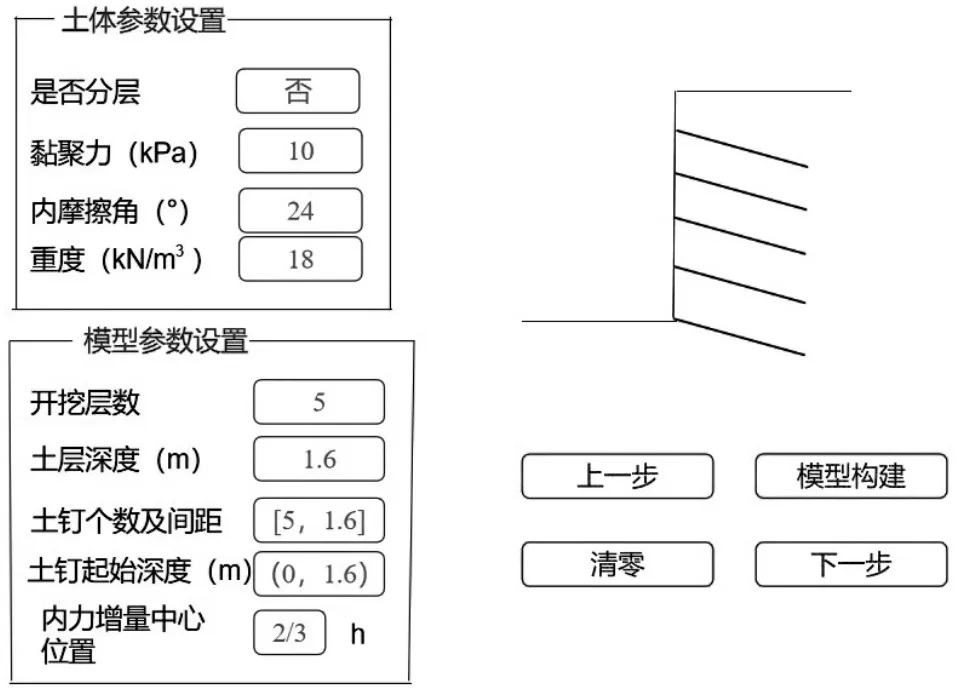
图5 参数输入图

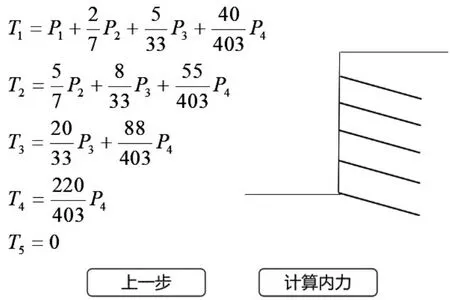
图6 内力公式输出图

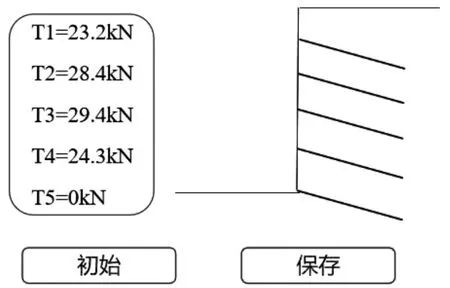
图7 结果输出图

3 算例分析

为检验计算方法合理性，以某垂直开挖基坑土钉支护进行分析，土体参数为c=10 kPa，φ=24°，γ=18kN/m3，临界高度Z0=1.97 m，第一层土层开挖至Z1=1.6 m处，后施工第一层土钉，之后土层每层开挖1.6 m，同时在土层底部施加土钉，共开挖为5层，如图8所示。

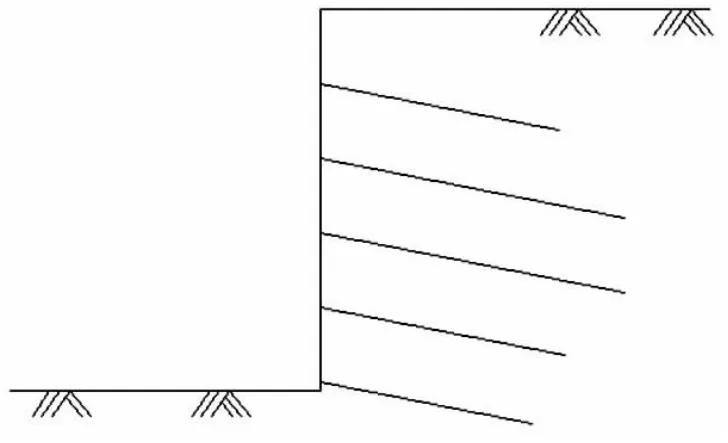
图8 土钉分布图

以单位宽度土体进行计算，根据朗肯土压力公式可求解侧向土压力，其应力分布如图9所示。

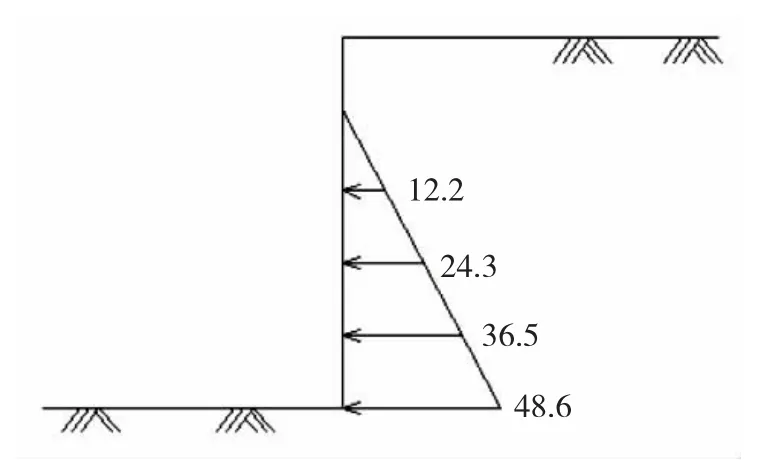
图9 朗肯土压力分布图

以往增量法经验表明将内力增量中心位置假定于开挖高度2/3处求解较为合理，故将土层中心位置假定为2/3深度并与规范法的土钉承担1/2面积进行比较，已验证两者差异，采用增量法各层土钉力内力增量为：

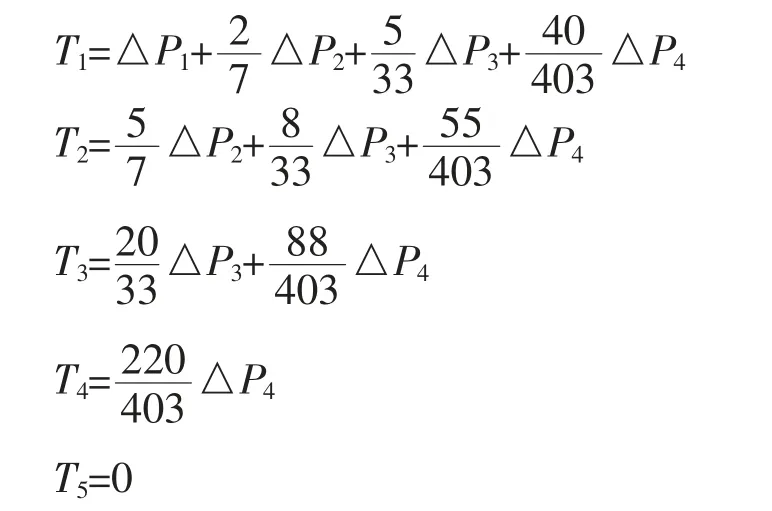
根据土体参数及开挖工况，将相关参数代入计算可得表1。

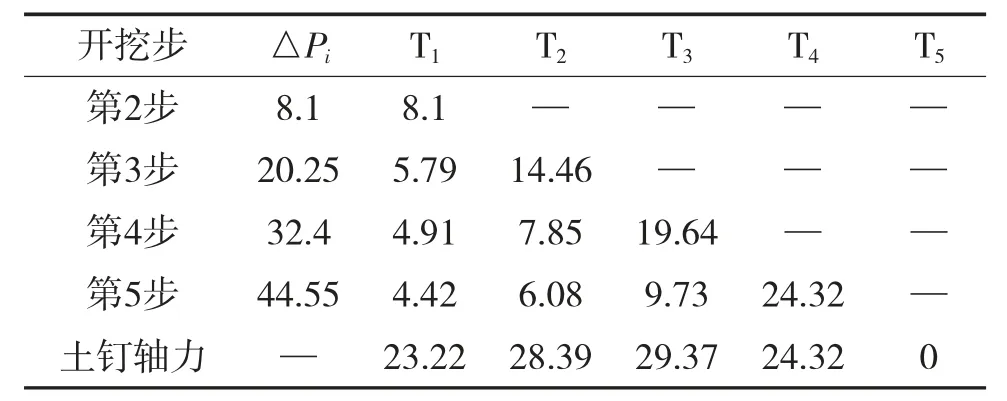
表1 土钉轴力值（单位：kN）

由于ΣTi=105.18 kN；Σ△Pi=105.3 kN。两者近似相等，差值为计算过程中约分造成的误差，该计算表明侧向不平衡土压力与土钉内力增量数值近似相等，即两者受力平衡。同时图6表明软件计算结果较为准确，有效减少人工计算中的繁琐过程和易产生的误差。

根据规范法中土钉承载1/2面积的朗肯土压力，计算可得土钉内力为：

如图10所示，规范法最下层土钉内力T5为36.45 kN，显然不合乎开挖完成后的施工最下层土钉的内力值，原因为规范法未考虑施工过程土压力变化的影响，将土钉视为一次施工完成后共同承担侧向土压力，故造成了上层土钉计算值较小，最下层土钉计算值偏大的结果。增量计算法考虑施工过程影响，较规范法更贴近于真实施工状况。

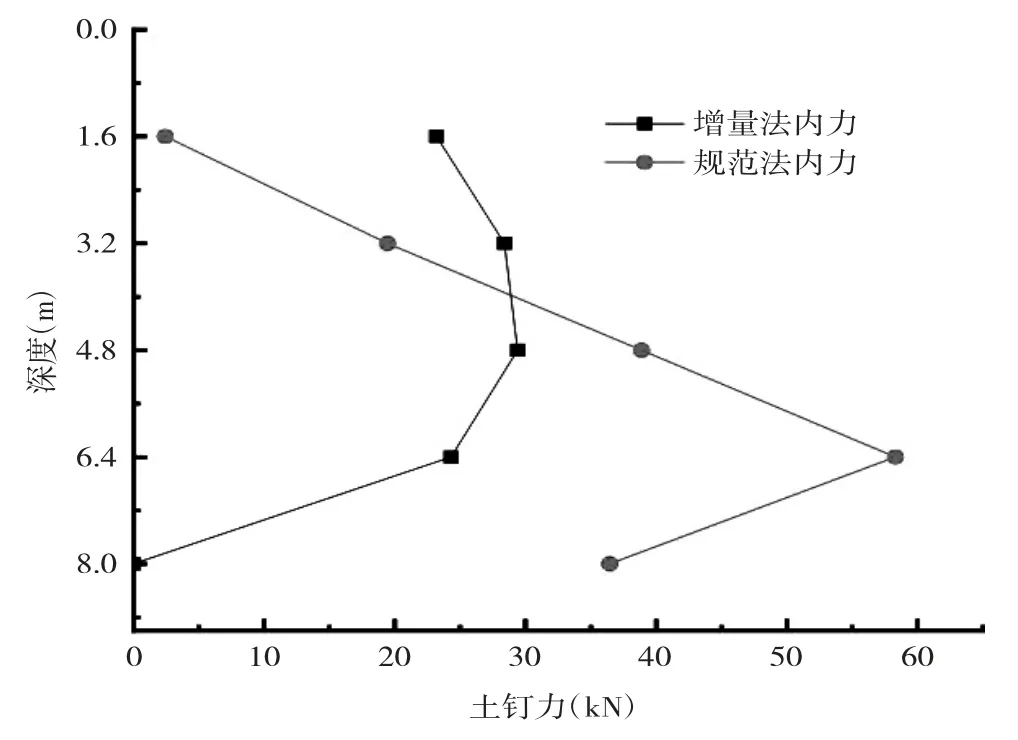
图10 不同计算方法土钉内力值

该算例选取较为简单的参数，旨在说明内力增量的计算方法和过程。实际计算时采用增量法考虑到了分布施工的特点，同时计算时可考虑不同坡角及层状土的影响。较于规范法而言增量法更合理地分配了侧向土压力，计算的土钉力分布与工程实测土钉力形状相似，表明该种方法的合理性。

4 结论

通过总结基坑开挖土钉施工过程，基于增量法探究土钉内力增量通用计算方法，使用MATLAB软件平台编制软件简化计算过程并输出结果。计算算例表明：土钉内力增量通用计算方法可有效考虑土体参数及施工开挖过程的影响，依据分步开挖过程和工程经验合理分配各层土钉内力增量；对比表明增量法内力计算结果较规程计算更加合理和准确；计算结果避免了规程计算中土钉内力上层较小、下层较大的现象；验证了实际工程中最下层土钉由于施工完成故增量内力较小的现象；土钉内力增量通用计算方法求解的内力分布更贴近于工程实际内力分布状态。