基于动态调整叶节点工序的综合调度算法

刘显超，赵 男，杨 茁，苏艳会，周 伟

（1 吉林师范大学 计算机学院，吉林 四平 136000；2 四平市第二十五中学，吉林 四平 136000；3 吉林师范大学附属学校，吉林 四平 136000；4 长春市第十六中学，长春 130000）

0 引言

产品的生产制造作为影响企业生产效率的主要因素，一直都是相关学科研究的热点。在人力资源、设备资源等有限的前提下，如何更好地提高生产加工的时间效率和设备的利用效率直接决定了企业的生产效率，也是制造业致力解决的重要问题。

随着互联网技术和计算机技术的发展，制造行业的产品需求和社会需求也发生了变化［1-5］。但是，人们对复杂产品的需求日趋个性化和多样化［6-7］，因而亟需解决多品种、小批量复杂工艺的产品调度问题。为此，有专家学者提出了将“产品的加工和装配同步处理”的综合调度［8］并开展了一系列的研究［9-12］，提出了诸多调度算法，也拓展出很多新的研究领域［12-18］。

虽然现有的综合调度算法已经取得了较好的研究成果，但是仍然存在横纵双向优化中兼顾性不完善的问题。例如以“工序”为研究对象的算法中，文献［13］虽然提出了以工序数量总量来确定调度路径和次序的算法，但是忽略了叶节点工序的重要作用。文献［14］虽然提出了以串行工序数量为排序策略的算法，但是忽略了设备利用率对整体调度效果的影响等等。

为解决上述问题，本文以优化综合调度时间成本为目标，提出了基于动态调整叶节点工序的综合调度算法。算法以复杂产品工艺树的叶节点工序和对应的加工设备作为研究对象，首先以复杂产品工艺树原始树图构建叶节点工序和对应加工设备的工序组，在工序组中优先调度层优先级较高的叶节点工序；其次，在工艺树中删除已调度的叶节点工序，重构复杂产品工艺树和叶节点工序，更新叶节点工序和对应加工设备的工序组；如此循环分解，直到原始工艺树中所有工序全部调度完毕的综合调度方法。

1 相关定义

假设综合调度系统有m台加工设备，需要加工完成复杂产品的n道工序，要求如下：

（1）在加工的某个时刻，加工设备只能连续加工对应的工序。

（3）不存在相同设备。

定义1 叶节点工序在复杂产品工艺树中，将没有紧前工序约束、但是具有紧后约束工序的工序定义为叶节点工序，且叶节点工序数量必须大于等于1。

定义2 工序层优先级根据文献［20］首次提出的层优先级问题，描述为：对于具有n层结构的复杂产品，首先将根节点工序的优先级设为最低，定义为1，根节点工序的所有后裔节点工序的优先级定义为2，以此类推，直到第n层的所有节点的优先级设为最高，定义为n［19］。

定义3 工序组在综合调度中，处于当前复杂产品工艺树中的叶节点工序和其对应的加工设备组成的加工组合定义为工序组。在工序组中，一台设备至少对应一道叶节点工序。

2 算法设计

复杂产品加工的全过程中，所有加工设备彼此独立，设备间不存在优先顺序的问题。本文分别从横纵两个方面优化了复杂产品的综合调度效果，其中纵向优化是通过在工序组调度的叶节点工序实现的，达到缩短整体加工用时的优化目标；横向优化是通过循环产生新叶节点工序实现的，即通过提高串行工序的紧密衔接度，减少对应设备上工序加工的间隔时间，达到提高各个设备利用率的优化效果。算法流程如图1 所示，具体阐述如下：

图1 算法流程图Fig. 1 Flow chart of the algorithm

Step 1以复杂产品工艺树原始树图为基础，查找所有叶节点工序。

随着我国经济不断发展，各种新科学、新技术层出不穷，各个行业都取得了一定程度上的发展，电力行业也是如此，它们抓住机遇，不断引进新技术，加之自己的创新，取得了不错的成绩，为我国国民经济的发展以及人民生活水平的提高做出重要贡献。输电线路是电力系统的重要组成部分，其安全性与稳定性直接影响到电力的有效供应。电力企业如何做好输电线路管理工作，已成为业内人士关注的重要问题。

Step 2建立叶节点工序组。

Step 3判断工序组中待调度叶节点工序是否唯一，是则调度；否则转Step4。

Step 4按照层优先级由高到低的顺序依次调度组内叶节点工序。

Step 5在复杂产品工艺树原始树图中删除已经调度完成的叶节点工序，形成新的工艺树。

Step 6重复Step1，直到根节点工序调度完毕。

3 调度实例演示

现假设复杂产品A加工工艺树如图2 所示。需要说明的是，此算例不特指某一类产品，对于其他小批量、多品种的复杂产品亦适用。对实例流程拟做阐释分述如下。

图2 复杂产品A 工艺树图Fig. 2 Complex product A process tree

Step 1以复杂产品工艺树原始树图为基础，确定原始工艺树图叶节点工序，共计9 道，如图3 所示。

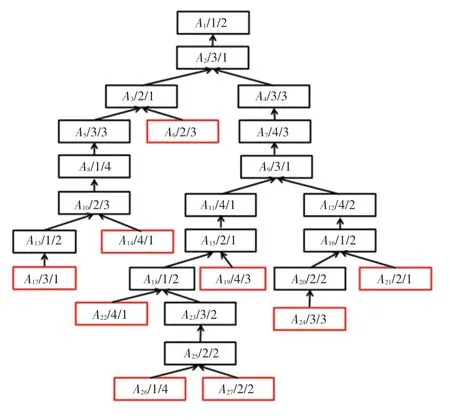
图3 复杂产品A 工艺树图初始叶节点工序图Fig. 3 Initial leaf node process diagram of complex product A process tree diagram

Step 2建立叶节点工序和对应加工设备工序组，可表示为：M1：｛A26／1／4｝；M2：｛A6／2／3、A21／2／1、A27／2／2｝；M3：｛A17／3／1、A24／3／3｝；M4：｛A14／4／1、A19／4／3、A22／4／1｝。

Step 3设备M1工序组中待调度叶节点工序只有A26，直接调度；设备M2、M3、M4对应的工序组中，叶节点工序不唯一，则按照层优先级由高到低的顺序依次调度组内叶节点工序，得到各工序组调度顺序为M1：｛A26／1／4｝；M2：｛A27／2／2、A21／2／1、A6／2／3｝；M3：｛A24／3／3、A17／3／1｝；M4：｛A22／4／1、A19／4／3、A14／4／1｝。

Step 4在复杂产品工艺树原始树图中删除已经调度完成的叶节点工序，形成新的工艺树，得到新的叶节点工序3 道，如图4 所示。

图4 第一次调度结束后的新树图Fig. 4 New tree after the first scheduling

Step 5重复上述步骤，直到根节点工序A1调度完毕，调度过程见表1。

表1 复杂产品A 调度过程表Tab.1 Scheduling process of complex product A

复杂产品A按照动态调整叶节点工序方法，调度顺序为：｛A26，A27，A21，A6，A24，A17，A22，A19，A14，A13，A25，A20，A16，A10，A23，A18，A8，A12，A15，A5，A3，A11，A9，A7，A4，A2，A1｝，调度甘特图如图5 所示，共计27个加工用时。

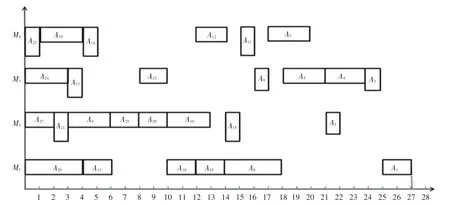
图5 本文算法加工复杂产品A 甘特图Fig. 5 Gantt chart of complex product A processed by this algorithm

4 算法对比分析

4.1 与文献［13］的算法对比

文献［13］的算法，按照紧密程度将复杂产品的所有工序分为2 类，对于紧密度较高的工序组采用“首次适应调度”算法，对于紧密度较弱的工序组使用“拟关键路径法”，调度顺序为｛A24、A21、A26、A27、A25、A23、A22、A19、A18、A15、A11、A20、A16、A12、A9、A17、A14、A13、A10、A8、A5、A6、A3、A7、A4、A2、A1｝，如图6 所示，总用时28 工时。

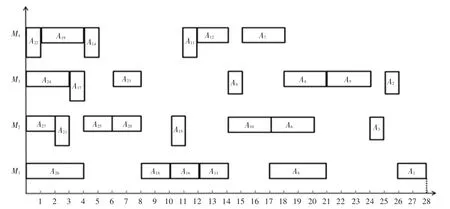
图6 文献［13］算法甘特图Fig. 6 Gantt chart of the algorithm in Ref.［13］

对比分析本文算法和文献［13］的算法对应的加工甘特图5 和图6 可知，本文算法中各个加工设备不相同且彼此独立，所以在满足紧前工序（组）约束前提下，设备M3在t ＝16 时刻调度工序A9，充分利用了设备M3在t ＝16 到t ＝18 时刻的空闲段。同时，因工序A5在图5 中比在图6 中早3 个工时开始加工，其紧后工序（组）A3、A2、A6的加工时间比在图6中分别提前了3、1、1 个工时开始加工。在设备M2上，本文算法从t ＝0 到t ＝13 时刻一直连续加工，处于“设备忙” 的状态，提高了M2的设备利用率。在设备M1上本文算法因工序A13从t ＝4 时刻开始加工，比图6 中的t ＝12 时刻提前了8 个工时开始加工，其后续工序A8、A3分别提前了3 个工时开始加工。对比分析表明，本专利方法能够有效减少对应加工设备的空闲时间，并提高了加工工序的紧密衔接度，进而优化了复杂产品整体调度效果。

4.2 与文献［14］算法对比

文献［14］算法在复杂产品工艺树的整体结构的基础上，首先将工艺树按照排序策略划分为只具有串行关系的工序序列，然后从调度方案集合中按照择时策略依次选择加工总用时最小和最早的方案进行调度。

针对复杂产品A的加工工艺树，采用文献［14］算法形成初始调度方案为｛A1、A2、A4、A7、A9、A11、A15、A18、A18、A25、A26｝，在此基础上按照｛A3、A11、A9、A13、A17、A19、A16、A20、A24、A6、A19、A27、A21、A14、A22、A26｝ 的顺序进行调整，结果甘特图如图7 所示，总加工用时为31 工时。

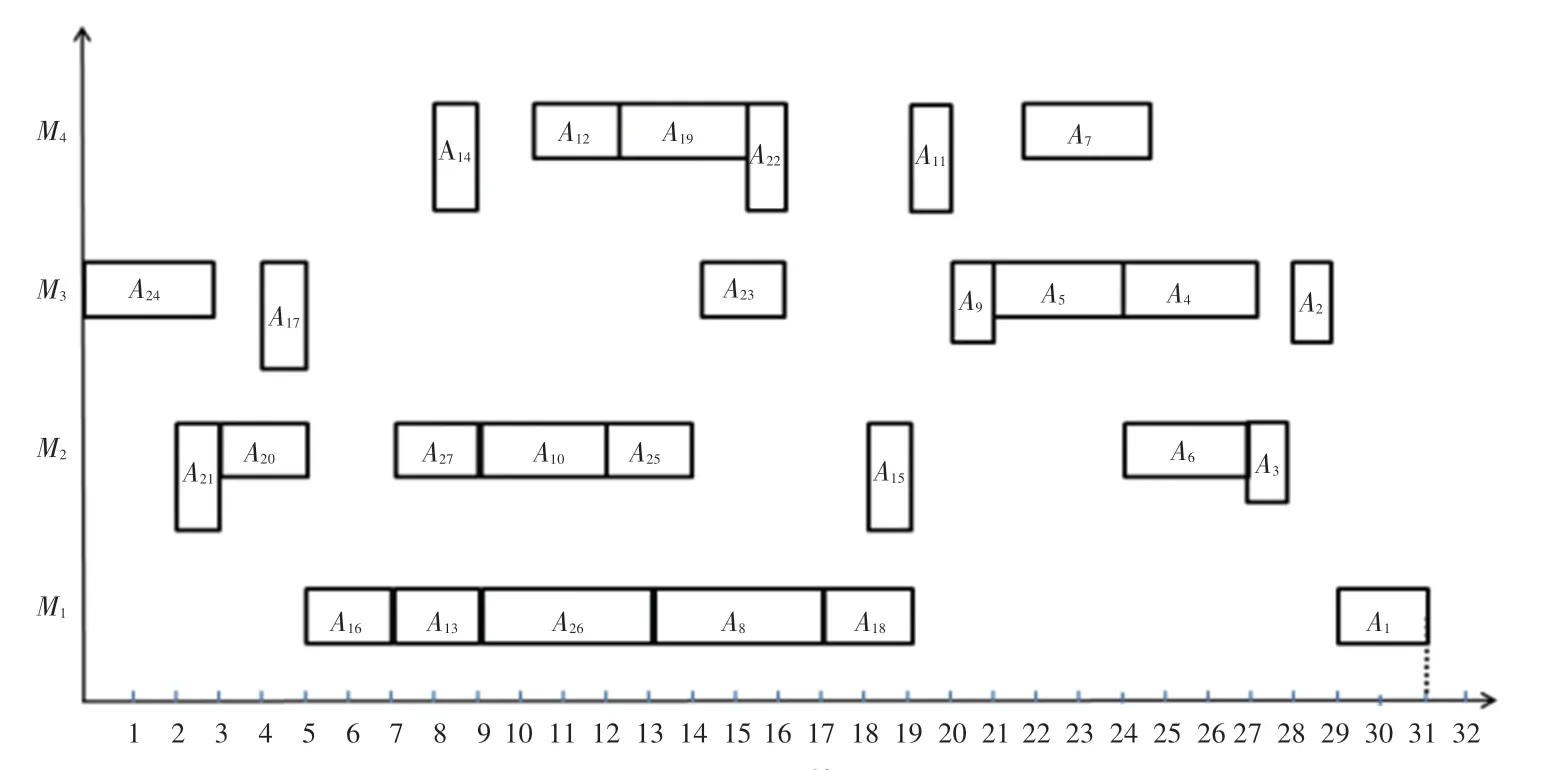
图7 文献［14］算法甘特图Fig. 7 Gantt chart of the algorithm in Ref.［14］

对比分析本文算法和文献［14］的算法对应的加工甘特图5 和图7 可知，本文算法所有设备均从t＝0 时刻的始点开始加工，整体上比文献［14］算法中的各工序衔接度要高。

在设备M4上，图5 在t ＝20 时刻完成了对应所有工序的加工，而图7 中在设备M4上所有工序加工结束前在t ＝0 至t ＝8 时刻、t ＝9 至t ＝10 时刻、t ＝16 至t ＝19 时刻、t ＝20 至t ＝22 时刻出现共计14 个工时的设备空闲时间段，明显多于图5 中的9 个工时的空闲时间段，设备M4利用率提高了11%。

在设备M3上，图5 在t ＝25 时刻完成了对应所有工序的加工，而图7 中在设备M3上所有工序加工结束前在t ＝3 至t ＝4 时刻、t ＝5 至t ＝14 时刻、t ＝16 至t ＝20 时刻、t ＝27 至t ＝28 时刻出现共计15 个工时的设备空闲时间段，多于图5 中的11 个工时的空闲时间段，设备M3利用率提高了7.7%。

在设备M2上，图5 在t ＝22 时刻完成了对应所有工序的加工，而图7 中在设备M2上所有工序加工结束前在t ＝0 至t ＝2 时刻、t ＝5 至t ＝7 时刻、t ＝14至t ＝18 时刻、t ＝19 至t ＝24 时刻出现共计13 个工时的设备空闲时间段，明显多于图5 中t ＝13 至t ＝14 时刻、t ＝15 至t ＝21 时刻共计7 个工时的空闲时间段，设备M2利用率提高了14.6%。

在设备M1上，图5 在t ＝27 时刻完成了对应所有工序的加工，而图7 中在设备M1上所有工序加工结束前在t ＝0 至t ＝5 时刻、t ＝19 至t ＝29 时刻出现共计15 个工时的设备空闲时间段，多于图5 中t ＝6 至t ＝10 时刻、t ＝18 至t ＝25 时刻共计11 个工时的空闲时间段，设备M1利用率提高7.7%。

综上，从各个设备利用率的角度分析，本文算法采用将对应设备与动态调整产生的叶节点工序进行组合的方法，是从工序和设备两个角度进行优化，对比分析表明本文算法不仅减少了各个设备的空闲时间段，而且提高了所有加工设备的利用率，进而提高了复杂产品加工的设备总体利用率。3 种算法的调度过程时间对比和设备利用率对比见表2。

表2 3 种算法的调度过程时间对比和设备利用率对比Tab.2 Comparison of scheduling process time and equipments utilization of three algorithms

4.3 3 种算法调度结果对比分析

对图1 中的复杂产品A，文献［13］的算法总加工用时为28 工时、文献［14］的算法总加工用时为31 工时，而本文算法总加工用时为27 工时。由此可知，本文算法更优，主要是因为：

文献［13］的紧密衔接工序组联动的算法虽然注重衔接紧密的工序组，但工序组中只由工序组成，不仅忽略了紧密衔接度不高的其他工序的相对位置等因素对调度结果的整体影响，而且没有充分利用设备的空闲时间段。例如，设备M2在t ＝17 至t ＝23时刻、设备M3在t ＝8 至t ＝14 时刻和设备M4在t ＝5 至t ＝11 时刻出现较长时间的空闲。

文献［14］ 中考虑串行工序紧密度的择时算法与紧密衔接工序组联动的算法相似，也是只以工序为主要优化对象，通过择时调度策略确定串行工序加工开始时间点，同样没有充分考虑到设备的利用率问题，忽略了设备因素在综合调度中的重要作用。例如设备M1在t ＝18 至t ＝29 时刻、设备M3在t ＝5 至t ＝14 时刻、设备M4在t ＝1 至t ＝8 时刻这些时间段一直处于空闲状态，没有加工工序，因此就给复杂产品加工过程造成一定的整体影响。

相对于紧密衔接工序组联动算法、考虑串行工序紧密度的择时算法，本文算法的设备利用率分别提高了0.8%、10.5%，实验表明本文算法在复杂产品的综合调度中效果更优，不仅为解决一般复杂产品的综合调度提供了一种新的方法，而且为进一步深入研究综合调度拓展了思路，具有一定的理论和实际意义。

5 结束语

综上所述，本文以优化复杂产品综合调度的时间成本目标，以复杂产品工艺树结构中具有重要作用的叶节点工序为优化对象，提出了基于动态调整叶节点工序的算法。实验对比分析表明，本文算法有效地提高了设备的利用率，为综合调度提供了一种新的研究方法。