疲劳载荷作用下无砟轨道混凝土轨道板碳化行为的数值模拟
陈宣东 章青 顾鑫 夏晓舟 林其武
河海大学 力学与材料学院,南京 211100
随着社会经济的飞速发展,温室气体的大量排放导致大气中二氧化碳(CO2)浓度显著增加,荷载与环境(CO2)耦合作用加速了高速铁路无砟轨道混凝土板的劣化进程[1-2]。环境中CO2通过混凝土的孔隙结构渗透到混凝土内部,与混凝土孔溶液中的氢氧化钙[Ca(OH)2]发生化学反应[3-4],生成碳酸钙(CaCO3),降低了混凝土的碱性,破坏了钢筋周围在碱性环境中形成的钝化膜,从而诱发了钢筋锈蚀,导致了轨道板保护层的开裂、剥落,劣化了轨道板的力学性能[5]。此外,高速列车的高频荷载促使混凝土内部的微裂纹成核和扩展,劣化了轨道板的微结构[6],加速了CO2在轨道板中的扩散和混凝土碳化进程。因此,研究疲劳荷载作用下轨道板的碳化行为对于保障轨道板在服役期内的安全运营具有重要意义。
国内外学者基于质量守恒定律、Fick 第二定律、化学反应律等,构建了各种经验和半经验的混凝土碳化理论模型[7-10]。其中,最具代表性的是Papadakis 模型[9]和Saetta 模型[10]。Papadakis 模型注重水泥水化以及CO2与混凝土矿物成分的化学反应过程,将CO2与水泥水化产物发生的化学反应耦合到水泥水化体系中,构建了基于化学反应平衡方程的混凝土碳化理论模型。Papadakis 模型不仅可以评估任意时刻水泥水化和碳化产物含量,如水化硅酸钙(CSH)、氢氧化钙(CH)等,还可以评估碳化产物对混凝土孔隙率的影响,但Papadakis模型参数众多且部分参数难以通过试验标定。Saetta 模型认为混凝土的水化反应在前期基本已经完成,主要考虑环境湿度、温度等因素对混凝土碳化速率的影响,并采用等效水化时间反映混凝土中的孔结构演化对CO2、水等物质传输的影响,极大地简化了混凝土碳化的建模过程。基于Saetta模型,Han等[11]通过引入混凝土随机骨料模型,研究了混凝土细观特征对混凝土碳化行为的影响;在此基础上,Shi等[12]则通过ABAQUS 模拟混凝土的破坏过程,研究了应力损伤对混凝土碳化行为的影响。研究表明:由于受载损伤区域存在微裂纹带,为CO2的扩散提供了快速通道,该类损伤区域出现了完全碳化现象。
尽管静载作用对混凝土碳化行为的影响已经取得了相关的研究成果,但疲劳荷载对碳化行为的影响不同于静载,具有显著的差异性[13-15]。在高速列车高频荷载作用下,随着荷载循环次数的增加,轨道板内部逐渐出现微裂纹,进而形成贯穿性的宏观裂纹[13]。疲劳裂纹极大促进了CO2的扩散并加速了轨道板的劣化进程。马昆林等[2]基于试验研究了碳化对CRTSⅢ型板式轨道板力学性能的影响,指出碳化降低了CRTSⅢ型板式轨道板的韧性,增加了疲劳荷载作用下CRTSⅢ型板式轨道板破坏的风险。Jiang 等[13]基于蒙特卡洛法建立了疲劳荷载作用下混凝土材料的碳化数值模型,研究表明,累计疲劳损伤将导致钢筋混凝土结构不同区域碳化深度差异明显。虽然现有研究对疲劳荷载作用下混凝土碳化行为做了一些理论及数值模拟研究[14-15],但是主要集中在基于试验数据对疲劳荷载CO2扩散系数的修正,缺乏列车荷载效应对碳化影响的研究。然而,轨道板不同位置对列车荷载的响应具有较大差异性,同时,混凝土细观结构具有非均质性[16-17],导致轨道板的碳化具有非均匀性。因此,有必要建立疲劳荷载作用下轨道板的碳化模型,以研究高速铁路疲劳荷载特性对轨道板碳化行为的影响。
本文考虑疲劳荷载对CO2扩散系数的影响,基于应力水平-疲劳寿命曲线(S⁃N曲线),构建以疲劳荷载作用次数为自变量的CO2扩散系数影响函数,修正Saetta 碳化模型的扩散项,建立一种新的疲劳荷载作用下轨道板混凝土的碳化模型,根据实测的位移时程数据进行有限元模拟计算,获得轨道板关键区域的荷载响应和碳化深度,分析疲劳荷载作用次数、应力水平、环境湿度等因素对轨道板碳化行为的影响。
1 疲劳荷载作用下混凝土的碳化模型
1.1 混凝土碳化的基本方程
基于Fick 第二定律、质量守恒和化学反应方程,Saetta 等建立考虑湿、热耦合效应的混凝土碳化反应控制方程[8]。
碳化过程方程为
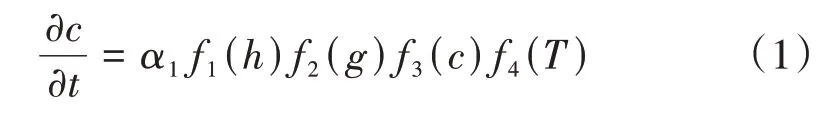
水分迁移方程为
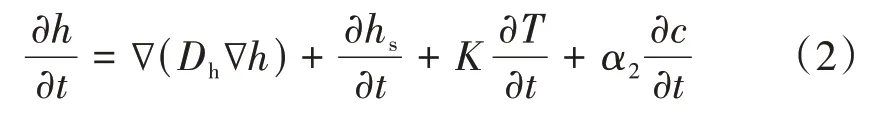
热传导方程为

式(1)—式(4)中:c、h、T和g分别为相对碳化度、湿度、温度和CO2体积分数;α1为理想状态下碳化反应速率;α2、α3和α4分别为碳化对水分、温度和CO2传输的影响系数;f1(h)、f2(g)、f3(c)及f4(T)分别为湿度、CO2体积分数、相对碳化度和温度对碳化速率影响函数,其详细表达式参见文献[8];∂hs/∂t为水泥水化消耗水分速率,由于混凝土在养护28 d 后,水泥水化度大于80%,与其他项相比,此项的值较小可以忽略不计;K为湿热系数;∂Qh/∂t为水泥水化放热速率,可以忽略不计;ρ为混凝土密度;Cq为混凝土比热容;b为传热系数;Dh和Dg分别为湿度和CO2的扩散系数;∇为梯度算子。
Dh和Dg与温度、湿度、相对碳化度、疲劳损伤等因素有关,可以表示为[7,11]
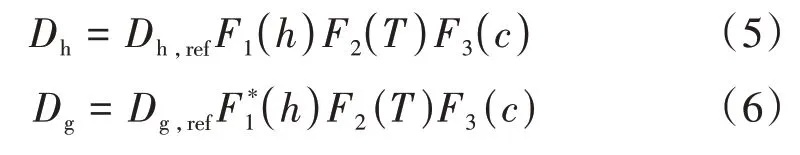
式(5)—式(6)中:Dh,ref、Dg,ref分别为参考湿度扩散系数和CO2扩散系数;F2(T)、F3(c)分别为温度及相对碳化度对湿度、CO2扩散系数的修正系数;F1(h)、F*1(h)分别为湿度对湿度扩散系数、CO2扩散系数的修正系数,具体可见参考文献[7,11]。
1.2 考虑疲劳损伤效应后扩散系数的修正
高速列车高频荷载对混凝土轨道板的劣化行为可以采用S⁃N曲线表征[18]。考虑到CRTSⅢ型板式轨道板的材料为C60 高强混凝土,其极限拉弯强度远小于抗压强度,故重点关注混凝土的拉弯疲劳损伤。虽然缺少轨道板的疲劳试验实测S⁃N曲线,但经文献调研采用如下S⁃N曲线[18]:
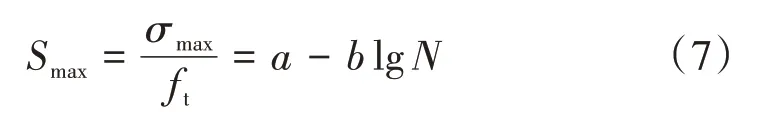
式中:Smax为应力水平;ft为混凝土抗拉强度;σmax为单次疲劳荷载循环过程中的最大应力;a和b为疲劳试验参数,本研究分别取0.942 和0.045[18];N为极限疲劳次数,即达到疲劳寿命时的最大疲劳次数。
在疲劳荷载循环0次和n次之后,有
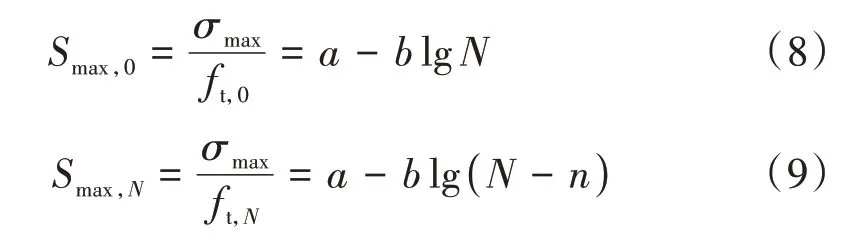
根据式(8)和式(9),得到
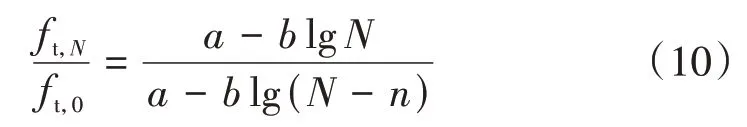
假定经过n次疲劳荷载循环,轨道板的疲劳损伤为dn,则有
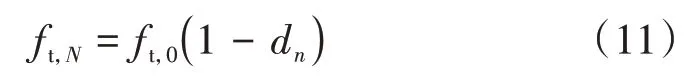
将式(11)代入式(10),有
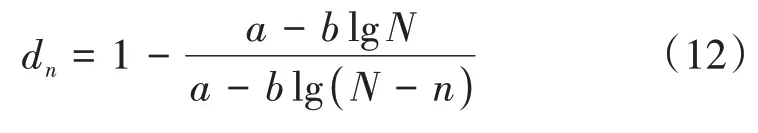
Ožbolt 等[19]基于连续介质力学的框架,遵循不可逆热力学的基本原理,建立了轨道板损伤与介质传输系数影响函数,模型经试验验证并被后续学者广泛采用。基于文献[19]提出的损伤标量与介质传输系数影响函数,对于n次疲劳荷载循环,疲劳损伤对湿度及CO2扩散系数的修正系数f(dn)可表示为[19]
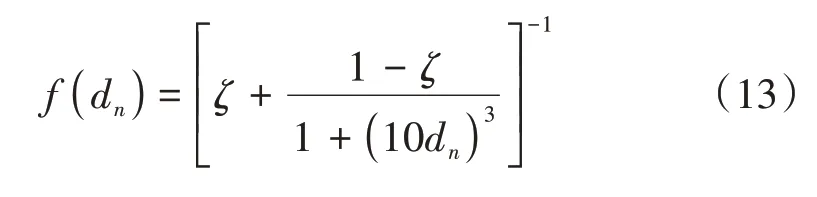
式中:ζ为混凝土完全损伤时的介质扩散系数与初始状态下介质扩散系数的比值。
2 疲劳载荷作用下轨道板碳化行为的数值模拟
2.1 研究对象
如图1(a)所示,以CRTSⅢ型板式轨道板作为研究对象,轨道板的几何尺寸为5.6 m × 2.5 m。由于混凝土的碳化深度在毫米级别,如对轨道板整体进行数值模拟计算,将会导致计算效率低下。为此,将轨道板简化为平面问题,并考虑轨道板、轨道板下方的自密实混凝土充填层和混凝土底座板的共同作用,并在混凝土底座板施加弹簧支撑约束,计算简图见图1(b)。
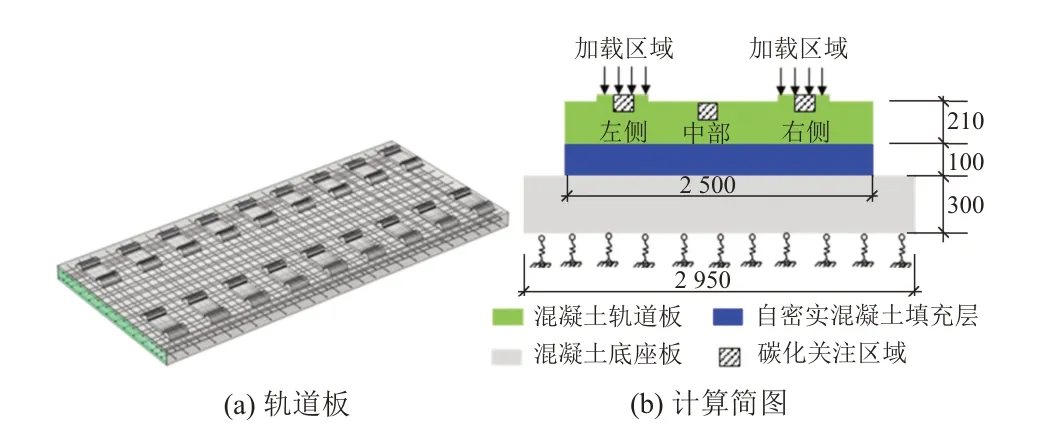
图1 CRTSⅢ型轨道板及计算简图(单位:mm)
2.2 计算条件和计算参数
在单次列车疲劳荷载作用下,混凝土的抗压强度远大于单次疲劳荷载的应力峰值,故可假定轨道板混凝土为线弹性材料。在进行碳化计算时,分别选取轨道板左侧轨道下方、中部和右侧轨道下方的100 mm ×100 mm 区域进行碳化分析,见图1(b)中的阴影部分。考虑混凝土细观结构对碳化行为的影响,采用混凝土随机骨料模型[20-22],骨料形态为随机凸多边形,骨料率为45%,骨料粒径为5~20 mm,钢筋直径为16 mm,相应的随机骨料模型见图2。计算中采用CRTSⅢ型板式轨道板的材料力学性能参数,见表1[23]。
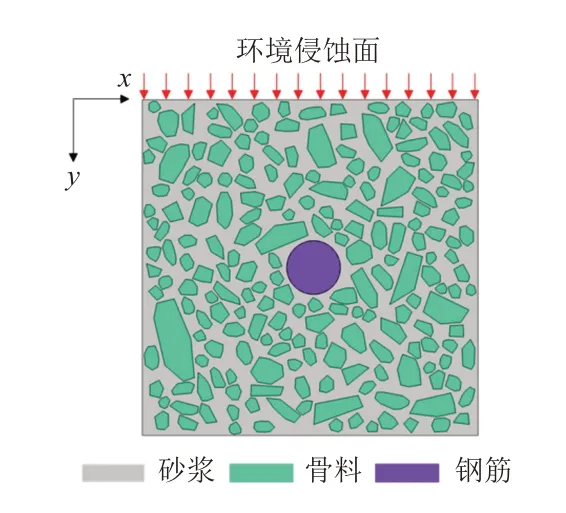
图2 关注区域混凝土的随机骨料模型
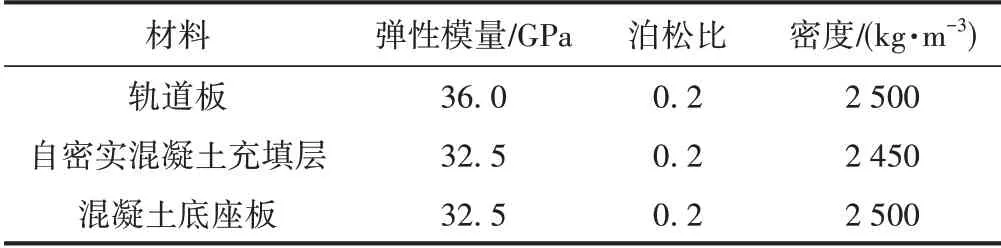
表1 材料力学参数
由于所取碳化关注区域中只有一侧是暴露在侵蚀环境中,因此,暴露在侵蚀环境中的温度边界条件采用随时间变化的周期性边界条件,CO2体积分数取0.035%[11],湿度取0.65,边界处的相对碳化度为1,侵蚀面的边界条件可以表示为

式中:t的单位为年。
对于轨道板而言,碳化深度是关注的重点,对于碳化关注区域的左右两侧边界处由于荷载相应的差异性及混凝土细观结构的随机性,会存在物质的交换,但是对碳化深度的影响可以忽略不计。同时,由于碳化是一个十分缓慢的过程[7],在轨道板服役寿命期内,碳化深度很难达到重点关注区域的底部。因此,除侵蚀面以外,其余边界条件均采用零通量边界条件。初始时刻,温度取293 K,CO2体积分数为0,湿度为0.85,相对碳化度为0,即未发生碳化。
碳化分析对象的应力水平通过在轨道顶部施加位移时程曲线,有限元分析轨道板力学响应获得。采用弹片式位移计实测,获得时速为155 km 的16 节车厢列车经过钢轨时,在左右轨道上产生的周期性位移荷载,见图3。
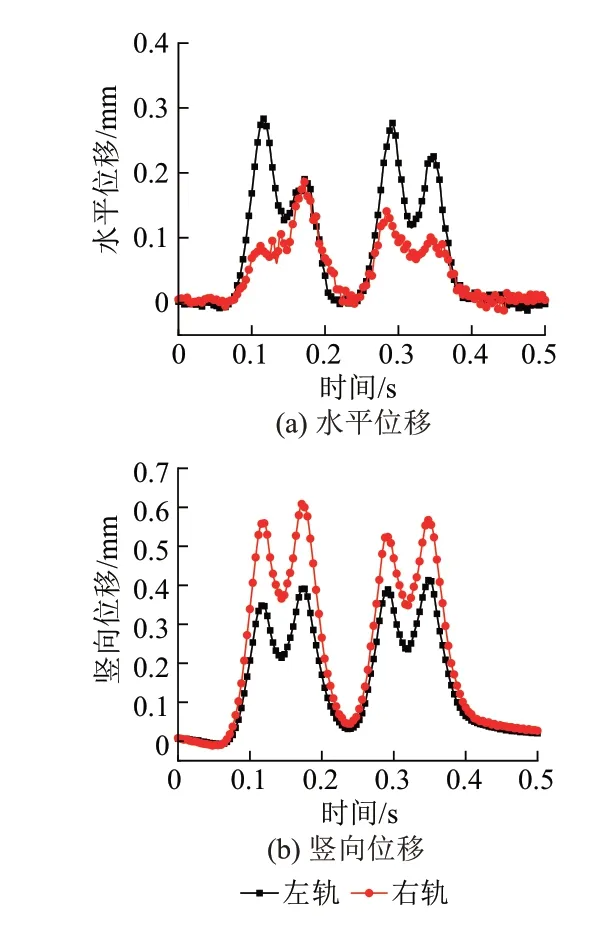
图3 轨道加载的位移时程曲线
2.3 计算流程
计算流程见图4,模型中计算参数取值见表2。
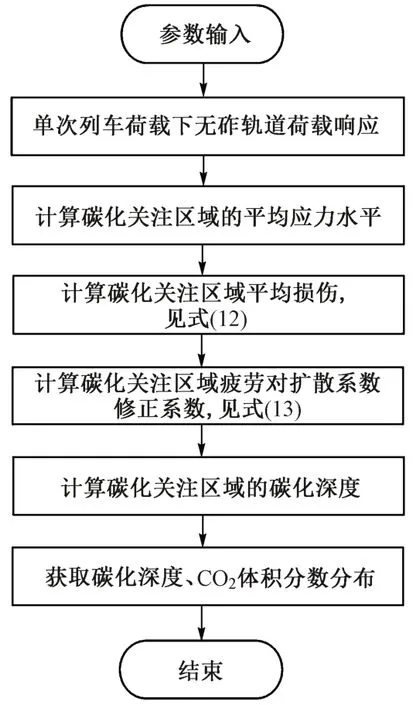
图4 计算流程
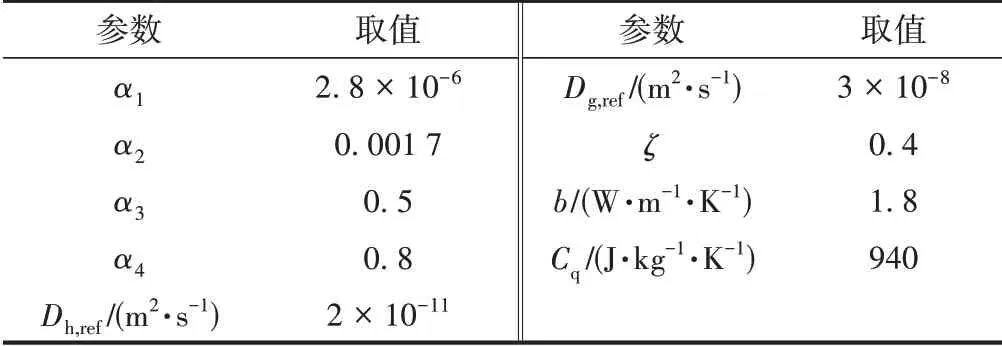
表2 碳化模型中计算参数取值
在数值模拟过程中,首先计算单次列车荷载作用下轨道板的力学响应,获取三个碳化关注区域的平均应力水平。其次,基于提出的以疲劳次数为自变量的CO2扩散系数修正模型,计算不同疲劳次数下碳化关注区域的CO2扩散系数。最后,计算湿度-温度-扩散-反应耦合方程组,以获取不同疲劳次数、不同侵蚀时间下,碳化关注区域的CO2体积分数、碳化深度分布,作为评估轨道板碳化的依据。
3 计算结果与讨论
3.1 轨道板不同区域的碳化深度
图5 给出了三个区域的平均应力时程曲线,最大应力分别为2.49、2.87、4.23 MPa。尽管荷载未直接作用在轨道板中部区域,然而,由于动力效应,轨道板中部区域的最大应力与左侧轨道下方最大应力差距较小。因此,轨道板中部区域依然是轨道板耐久性评估的重点关注区域。
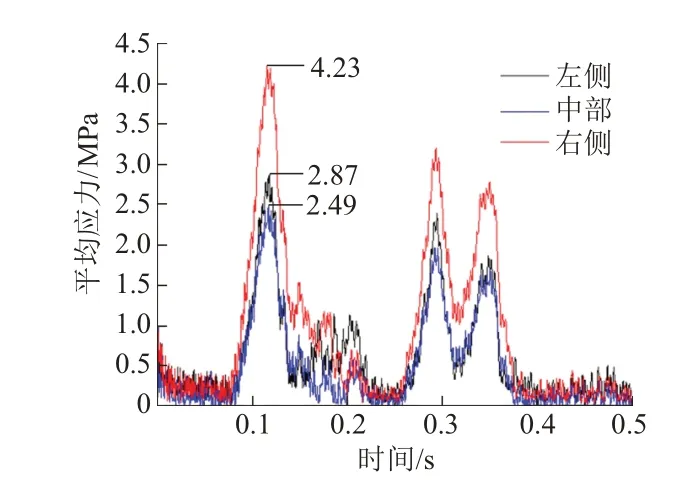
图5 计算区域内的平均应力时程曲线
图6 给出了碳化25 年三个区域的碳化深度,其中,施加的疲劳荷载次数为三个区域极限疲劳次数的最小值,其中极限疲劳次数依据式(7)计算。可知,右侧轨道下方碳化深度最为严重,碳化深度约为39.75 mm,左侧轨道下方及中部区域碳化深度几乎一致,约为28.76 mm。这主要是因为左侧轨道下方及中部区域的应力水平低于右侧轨道下方区域,施加的疲劳荷载次数远低于其极限疲劳次数,对混凝土产生的损伤很小,则两个区域的微小损伤对碳化的贡献比重可以忽略。由此可见,疲劳荷载循环次数及应力水平是影响轨道板碳化深度的关键因素。

图6 疲劳次数为三个区域极限疲劳次数的最小值条件下CO2侵蚀25年后相对碳化深度分布云图
3.2 疲劳荷载次数对碳化深度的影响
不同疲劳荷载次数下相对碳化度曲线见图7。可知,随着疲劳荷载次数增加,碳化深度先保持不变,然后逐渐增加。当疲劳荷载次数小于0.4N时,疲劳荷载对轨道板碳化行为的影响可以忽略不计;当疲劳荷载次数大于0.4N时,疲劳荷载显著地加速碳化速率。例如,当疲劳次数为0 时,在受环境中CO2侵蚀10 年时,轨道板碳化深度仅为17.25 mm;当疲劳荷载次数为0.9N时,CO2侵蚀10 年导致轨道板碳化深度为24.75 mm。与不考虑疲劳荷载效应相比,碳化深度增加了43.48%。因此,在对轨道板使用寿命后期健康状态评估时,应考虑疲劳荷载效应对碳化行为的影响。

图7 不同疲劳荷载次数下相对碳化度曲线
3.3 应力水平对碳化深度的影响
图8 显示了应力水平0.55 的疲劳寿命次数下,碳化25 年时,应力水平为0.50、0.55、0.60 工况下,轨道板的碳化深度分别为25.34、26.15、29.14 mm。与应力水平为0.65 的相比,应力水平为0.50 和0.55 的碳化深度降低了13.04%和10.26%,表明高应力水平的疲劳荷载极大地促进了轨道板的碳化。

图8 不同应力水平下轨道板相对碳化度云图
受环境中CO2侵蚀10 年后,不同应力水平下轨道板中CO2体积分数分布曲线见图9。可知,随着侵蚀深度的增加,CO2体积分数逐渐减小。结合图8 可以看出,在碳化和未碳化区域分界线(碳化前锋线)附近,CO2体积分数为0。

图9 不同应力水平下CO2体积分数分布曲线
3.4 湿度对碳化深度的影响
一方面,随着湿度的增加,湿度对碳化速率影响函数[f1(h)]值在逐渐增加;另一方面,随着湿度的增加,CO2在混凝土中扩散速率逐渐减小,混凝土中CO2体积分数在逐渐减小,导致CO2体积分数对碳化速率影响函数[f2(g)]值逐渐下降。f1(h)与f2(g)的乘积决定碳化速率,故湿度对碳化的影响具有双重效应。为了研究湿度对碳化深度的影响,模拟分析湿度为0.45~0.75时轨道板的碳化行为。
不同湿度下相对碳化度曲线见图10。可知,随着湿度增加,介于0 和1 之间的碳化过渡区在逐渐减小,这是较低的湿度下碳化反应速率较小而CO2扩散速率较高共同作用的缘故。
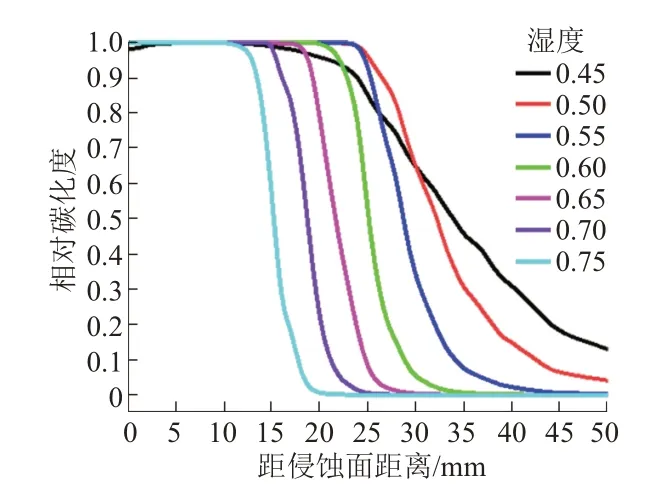
图10 不同湿度下相对碳化度
不同湿度下轨道板碳化深度见图11。可知,随着湿度增加,碳化深度逐渐减小,表明尽管湿度的增加促进了碳化反应,但湿度的增加也极大抑制了CO2的传输。因此,湿度在0.45~0.75 时,随着湿度的增加,碳化深度在逐渐降低。
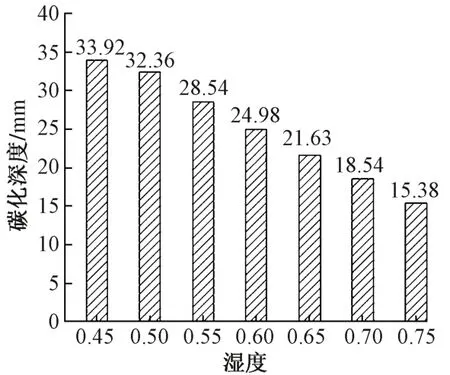
图11 不同湿度下碳化深度
4 结论
本文通过引入以疲劳次数为自变量的CO2扩散系数影响函数,修正了Saetta 碳化模型中扩散项,建立疲劳荷载作用下轨道板碳化模型,数值模拟了轨道板代表性区域混凝土二维细观结构的碳化行为,研究了疲劳荷载次数、应力水平及服役环境中湿度对轨道板碳化行为的影响。得到以下结论:
1)随着疲劳荷载次数的增加,碳化深度先不变,然后逐渐增加。因此,在对轨道板使用寿命后期服役健康状态进行评估时应当考虑疲劳荷载对碳化行为的影响。
2)在相同的疲劳荷载循环次数下,随着应力水平的增加,轨道板碳化深度显著增加,在实际工程中,应更加注重高应力水平区域疲劳荷载对轨道板的碳化行为的影响,必要时,可对高应力水平区域混凝土进行表面处理,以抑制混凝土碳化。
3)尽管湿度对混凝土碳化行为具有正负双重影响,但当湿度在0.45~0.75 时,CO2扩散性能对碳化深度起控制作用,随着湿度的增加,碳化深度在逐渐降低;因此,在实际工程中应当更加注重干旱地区轨道板的碳化行为。

