利用双晶格势进行硅的分子动力学模拟及其有效性
魏崇阳,张 辉,刘仲武,钟喜春,焦东玲,邱万奇,余红雅
(华南理工大学 材料科学与工程学院,广东 广州 510640)
1 前 言
硅(Si)是重要的半导体元素[1-8]。在过去的几十年中,基于实验理论的模拟计算方法在Si及其化合物的研究中发挥了重要作用[9]。随着研究对象尺度的不断减小,微/纳米尺度Si团簇的物理化学性质的实验研究变得越来越困难,原子尺度的计算模拟变得尤为重要。由于Si是共价晶体,原子之间由共价键结合,在原子尺度的计算中对共价键的描述十分困难。从理论上讲,密度泛函理论(DFT)计算可以给出最精确的计算结果,但即使是由数百个原子组成的系统也需要大量的计算时间以及非常高的计算能力,这使得量化计算适用范围受限。因此,在研究稍大系统的性质时,最常用的是基于相互作用经验势的分子动力学(MD)模拟方法,通过构造经验势,并且应用于分子动力学模拟中来计算系统的物性参数。
目前,Si的原子间作用势包括Tersoff势以及其修正势[10-13]、Stillinger-Weber(SW)势[14]、依赖于环境的原子间作用(EDI)势[15]、电荷优化多体(COMB)势[16]、修饰嵌入原子(MEAM)势[17]及其修正势等[18]。其中,Tersoff势、SW 势、EDI势和COMB 势是多体势。在这些作用势中,除了描述两个原子之间的相互作用的对势之外,还存在一个三体势,用以描述三个原子之间的相互作用或定义所谓的键角。此外,COMB势还考虑了电荷的影响。这些多体势可以为Si的某些物理性质提供适当的描述。许多研究者[10-18]通过计算基于不同作用势的Si的相关参数,例如弹性常数,结合能和径向分布函数等,来验证作用势的有效性。虽然这些物理参数反映了物质本身的某些属性,但最直接的验证标准应该是应用这些原子间作用势能否在分子动力学模拟中获得Si的金刚石结构。
研究表明,即使应用一个与实验数据非常符合的原子间作用势,在分子动力学模拟中也无法形成金刚石结构。例如,应用描述金属元素和合金中的嵌入原子(EAM)势[19],在分子动力学模拟中可以得到与实验一致的金属晶格结构[20-21]。然而在分子动力学模拟中应用上述原子间作用势,模拟系统却不能得到Si的金刚石结构,即上述作用势无法通过Si的晶体结构的验证测试。因此,本研究为Si构建了一个新的原子间作用势,利用该作用势在分子动力学模拟中得到了Si的金刚石结构,并据此获得了相关的物理参数,用以验证该作用势的有效性。
金刚石结构可以看作是两个面心立方(fcc)晶格的组合,其晶胞中有八个原子,因此可以从两个fcc晶格原子间作用势和两个晶格之间的原子间作用势出发构建金刚石结构。目前,用于fcc晶格的模拟主要为EAM 势[19-21],但是在EAM 势中引入的参数过多,很难定义两个fcc晶格之间的原子间作用。这里,仅考虑简单的Lenard-Jones(LJ)势。研究表明,在分子动力学模拟中LJ势的基态对应于六方密排(hcp)晶格(c/a≈1.633,a和c为hcp结构的晶格常数),这与计算结果一致[22-23]。在某些模拟情况下,系统还可以显示亚稳态fcc晶格[24]。将模拟结果与理想的hcp 和fcc晶格比较,可以鉴别出模拟系统的布拉格点阵。进一步的研究表明,在模拟系统中不设置任何初始布拉格点阵,利用几种LJ势的组合,构造出的双晶格(DL)势可以得到金刚石和石墨结构[25]以及更复杂的钙钛矿ABO3结构[26]。这些结果有助于理解和重新思考LJ势的重要性以及晶体结构的形成。
本研究在分子动力学模拟中通过构造双晶格势来获得Si的金刚石结构,并应用双晶格势获得了Si的结晶温度、晶格常数和弹性常数等物理参数,并与其他原子间相互作用势和实验测试结果进行了比较。
2 模型与模拟
2.1 模型
在双晶格作用势中,通过将两个fcc晶格原子间势和两个晶格之间的原子间势组合来描述晶体结构。用于描述fcc晶格的LJ势可表示为:

式中:ε是势阱的深度,σ原子间相互作用势为零的有限距离,r是原子之间的距离。
首先建立一个多原子相互作用的模型,在该模型中引入两种类型的原子,分别表示为S1和S2,它们在物理属性上彼此相同,对应于Si金刚石结构原子的两个自旋结构。例如,S1类型原子对应四个自旋向上,S2类型原子对应四个自旋向下。S1和S2原子的晶格和晶格常数相同。在其他模型中,所有Si原子都相同,而该模型中的S1和S2原子类型被视为两个可区分的Si原子类型。S1和S2晶格之间存在相互作用。在这里,LJ势应用于S1晶格,S2晶格以及S1和S2晶格之间的相互作用,原子之间的平衡距离和结晶温度由LJ势参数确定。
2.2 模拟过程
模拟过程中,在不设置任何初始布拉格点阵情况下,在模拟盒子中平均随机创建S1和S2原子。应用周期性边界条件,对于LJ势,截止距离表示为rc。系统的最高温度不高于温度T0(4 000 K),然后执行能量最小化过程。在T0温度下执行NPT 系综操作,时长为1 000 ps,时间步长为10-3ps。系统的温度从T0开始降低,步长为n。在每个温度T处执行一次NPT系综操作,持续时间为100~1 000 ps。在整个模拟过程中压力始终保持为零。表1列出了分子动力学模拟中LJ势的参数。

表1 分子动力学模拟中LJ势的参数Table 1 Parameters for LJ potentials in MD simulations
为了获得基于DL势的Si晶体应力与应变关系,在模拟系统中创建理想的Si晶体结构。S1和S2原子的初始fcc晶格具有相同的晶格常数(a=5.341Å),并且S1晶格相对于S2晶格在x,y和z方向上的相对位移分别为0.25、0.25 和0.25 个单位长度。在300 K的温度下执行NPT 系综操作,时长为1 000 ps。使晶体发生微小变形,之后计算由变形引起的应力值,并获得应力与应变的关系。由此,可以计算出弹性常数c11、c12和c44的值,计算代码参考文献[27]。
本研究还将基于DL势计算获得的物理参数与其他原 子 相 互 作 用 势(Tersoff、SW、EDI、COMB 和MEAM 势)的结果进行了比较。本次模拟的系统原子数分别为512、1 000和8 000。分子动力学模拟使用的软件为lammps[28],并通过VESTA[29]软件进行可视化分析。
2.3 模拟系统晶体结构识别
检查识别模拟系统显示为Si的金刚石结构是测试DL势有效性的首要条件。但是lammps软件缺乏识别模拟系统晶体结构的功能,因此本研究计算了模拟系统中原子之间的距离分布函数和原子与其最近邻原子之间的角度的分布函数,即ρ(d)和ρ(θ)。从lammps软件获得理想Si晶体结构,其分布函数由少量离散值组成。如果模拟的分布函数在这些相应位置显示为非零值,则可认为该系统具有与理想Si晶体相同的晶体结构,从而检查模拟系统与参考系统之间的差异以进行晶格识别。在模拟中,得到任一原子在特定时间和温度下的(x,y,z)坐标,可以计算出原子之间的距离及原子与其最邻近原子之间的角度。分布函数ρ(d)(或ρ(θ))表示距离d(或角度θ)在d-d+dd(或θ-θ+dθ)范围内的计数值或强度。在计算中,如果一个原子R及其最近邻原子之间的距离为dR,那么一个原子的最近邻原子数始终大于1,这些距离dR的最小距离为dm,并且dR的值不同。如果dR/dm<1.1,则该原子可被视为原子R的最近邻原子之一。
此外,分布函数ρ(d)与径向分布函数g(r)相似,但是它们的计算方法不同。角度θ是某些晶体结构(如金刚石结构)的键角。对于Si的晶格识别,为了计算分布函数,可将S1和S2原子视为同一种原子,也可将其单独用作S1(或S2)子系统。
3 结果与分析
3.1 晶体相变和结构识别
本研究根据DL 势和其他原子间势(Tersoff、MEAM、EDI、SW 和COMB势)计算了不同温度下Si原子系统的能量和体积。某些势会有一些修正版本,例如Tersoff的Tersoff-Mod(TM)势[12]和Tersoff-Mod C(TMC)势[13],以及MEAM 的MEAM-Spline(MEAMS)势[18]。图1 显示了每个原子的能量和每个原子的体积与温度的关系。图1(a)表明,对于所有作用势,系统的能量随着温度的降低而降低。特别是对于Tersoff势,模拟系统始终处于简单的结晶状态,一旦温度超过1 800 K,系统的体积就会迅速增加到无穷大,导致模拟失败。这意味着具有Tersoff势的系统将永远不会进入液态,并且始终显示金刚石结构。对于TM 势,系统可以进入液态。随着温度的降低,每个原子的能量不断减少,直到温度接近1 300 K,并且能量突然改变,表明存在相变。但是,在使用EDI、MEAM、MEAMS、SW 和COMB势进行的模拟中,系统体积随温度降低突然增加(见图1(b))。对于基于DL势的模拟还存在一个明显的热滞。从高温冷却时,能量和体积都会降低,并且存在液态晶态相变,这与实验现象一致。在DL 势的情况下,每个原子的能量在100 K 下约为2.18 eV,仅为其他作用势的一半。但是,该能量仍可以确保结晶温度与实验结果符合,体积值也与实验数据非常吻合(见表2)。
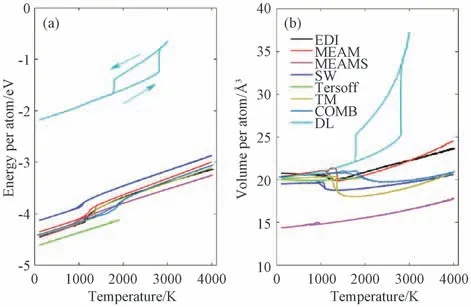
图1 基于不同作用势单原子的能量(a)和体积(b)与温度的关系Fig.1 Dependence of energy per atom(a)and volume per atom(b)on the temperature with different interatomic potentials applied
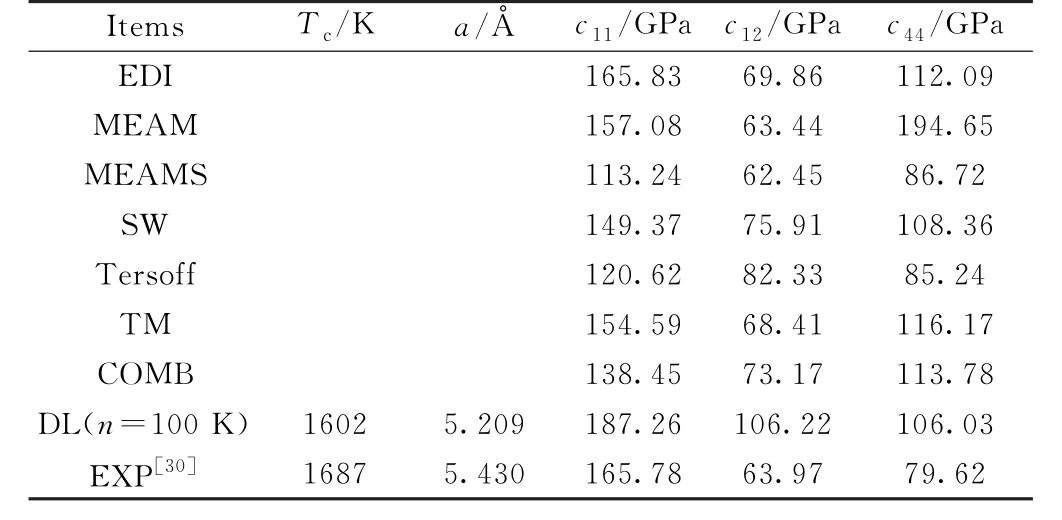
表2 基于不同原子间作用势获得的结晶温度T c、晶格常数a 和弹性常数(c 11,c 12,c 44)Table 2 Crystallization temperature T c,lattice constant a,and elastic constants(c 11,c 12,and c 44)obtained with different interatomic potentials applied
图2和3分别显示在T=100 K 和4 000 K 时,基于不同原子间作用势模拟得到的原子之间的距离ρ(d)和原子与其最近邻原子之间的角度ρ(θ)的分布函数。图2中,对于某些确定的d和θ,理想的金刚石结构的ρ(d)和ρ(θ)不为零。当系统冷却后,Tersoff势的ρ(d)和ρ(θ)与理想Si晶体结构的结构相匹配,表明Tersoff势有利于保持金刚石结构的稳定,而具有TM 势的系统显示出明显的不同。例如,在T=100 K时,ρ(θ)在109.5°处虽然有一个弱峰,但如图2(a)所示,它却不是晶态的,表明此刻Tersoff势模拟系统处于结晶状态和液态的混合状态。在T=4 000 K 时,所有的峰消失,所有系统都处于液态(见图3(a))。
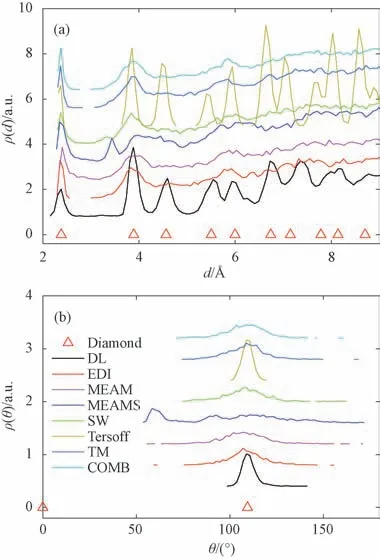
图2 基于不同作用势原子之间的距离ρ(d)和原子与其最近邻原子之间的角度ρ(θ)的分布函数(T=100 K;COMB势T=50 K)Fig.2 Distribution functions of the distances between atoms and the angles between the lines linking one atom with its nearest neighborsρ(d) (a)andρ(θ) (b)with different interatomic potentials applied at T=100 K.For COMB potential T=50 K
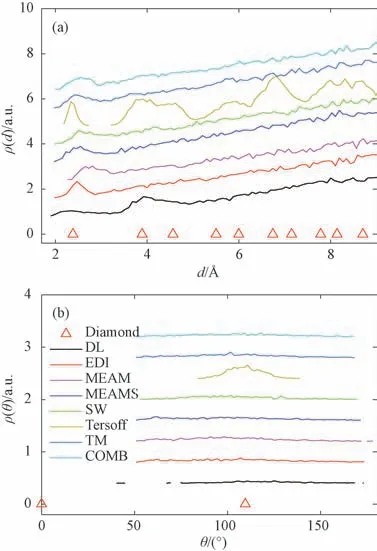
图3 基于不同作用势原子之间的距离ρ(d)和原子与其最近邻原子之间的角度ρ(θ)的分布函数(T=4000 K;Tersoff势T=1800 K;DL势T=3000 K)Fig.3 Distribution functions of the distances between atoms and the angles between the lines linking one atom with its nearest neighbor ρ(d) (a)andρ(θ) (b)with different interatomic potentials applied at T=4000 K.for Tersoff potential T=1800 K and for DL potential T=3000 K
图4显示了在T=100 K 时基于不同原子间相互作用势模拟所得到的原子排列。在图4(h)中,S1和S2原子分别由黑色和绿色点表示。图4(a)~(g)表明,具有Tersoff 势的系统始终是结晶的,具有MEAM、MEAMS、SW、EDI、TM 和COMB 势的系统显然是无序的。能量的异常变化可能意味着从一种液相转变到另一种非结晶相,如图1 所示。应用EDI、MEAM、MEAMS、SW 和COMB 势模拟时结果也与TM 势类似(见图2、3和4)。因此,从图1、2、3和4可以得出结论,使用MEAM、MEAMS、SW、EDI、TM 和COMB势,不能在分子动力学模拟中获得Si金刚石结构,也就没有晶格常数。

图4 基于不同作用势的原子排列(T=100 K;COMB势T=50 K)Fig.4 Atomic configurations with different interatomic potentials applied at T=100 K.For COMB potential T=50 K(a)EDI; (b)MEAM; (c)MEAMS; (d)SW; (e)Tersoff; (f)TM; (g)COMB; (h)DL
此外,在图2中,在DL势的情况下,即使ρ(d)的第七个峰显示出很小的偏差,ρ(d)和ρ(θ)也与参考的理想金刚石结构的数据一致。图3表明,在T=3 000 K时的ρ(d)和ρ(θ)与MEAM、MEAMS、SW、EDI、TM和COMB势相似。图4(h)表明,每个绿色原子拥有四个黑色最近原子,并且每个黑色原子也拥有四个绿色最近原子。然而,计算结果表明纤锌矿结构具有与金刚石结构相同的ρ(d)和ρ(θ),因此无法从ρ(d)和ρ(θ)分辨出确切的晶体结构。识别晶体结构需要检查子系统的晶格,对于金刚石结构,子系统显示为fcc晶格,对于纤锌矿结构,子系统显示为hcp晶格。
3.2 金刚石结构与fcc子晶格或hcp子晶格之间的关系
之前的研究表明,LJ 势的基态对应于hcp 晶格[24]。但是,由于fcc晶格的能量比hcp晶格的能量稍高[22-23],因此在LJ势下,系统还可以在某些模拟条件下显示fcc晶格[24]。在本研究的工作中,通过更改系统的冷却温度步长n,研究n对系统晶体结构的影响。图5为DL势的分子动力学模拟中,在不同温度步长n下,每个原子的能量和体积与温度的关系。当n=5 K时,系统显示出最低的能量和体积,以及最高的结晶温度(1 780 K)。体积随温度步长的增加略有增加。
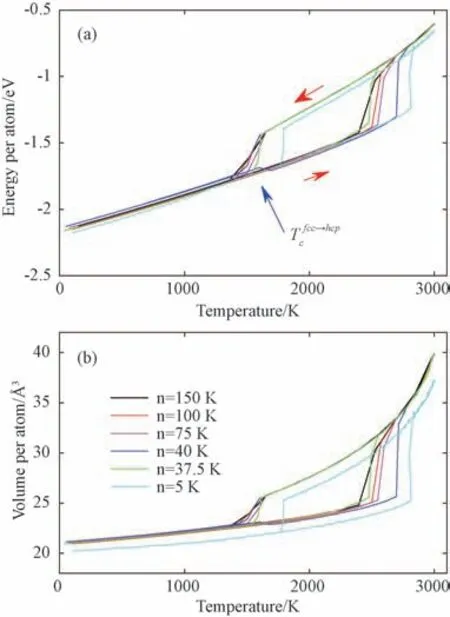
图5 基于DL势单原子的能量(a)和体积(b)与温度步长n 的关系Fig.5 Dependence of energy per atom(a)and volume per atom(b)on the temperature with different temperature steps n for DL potential
图6为在低温时基于DL势的分子动力学模拟中具有不同温度步长n时的ρ(d)和ρ(θ)分布函数。图6(a)、(c)和(e)中,ad和af分别代表金刚石结构和fcc晶格的晶格常数,如箭头所示。在图6(c)和(e)中,对于S1(或S2)子系统,晶胞的晶格常数为af,它对应于d2值,在该值处子系统在ρ(d)函数显示第二个峰值。d1值是原子之间的最短距离。从金刚石结构的ρ(d)函数来看,金刚石结构晶胞的晶格常数ad等于af。一个金刚石晶胞中有八个原子,因此,d2和d4分别是子系统的d1和d2,而d1和d3分别是S1和S2原子之间的距离。d1和d2已在DL 势中定义,但从模拟得出S1和S2原子之间的距离与DL势中定义的距离略有不同。对于fcc子晶格,存在的角度分别为60°,90°和120°,对于hcp 子晶格,存在的角度则分别为60°,90°,109.5°和120°。
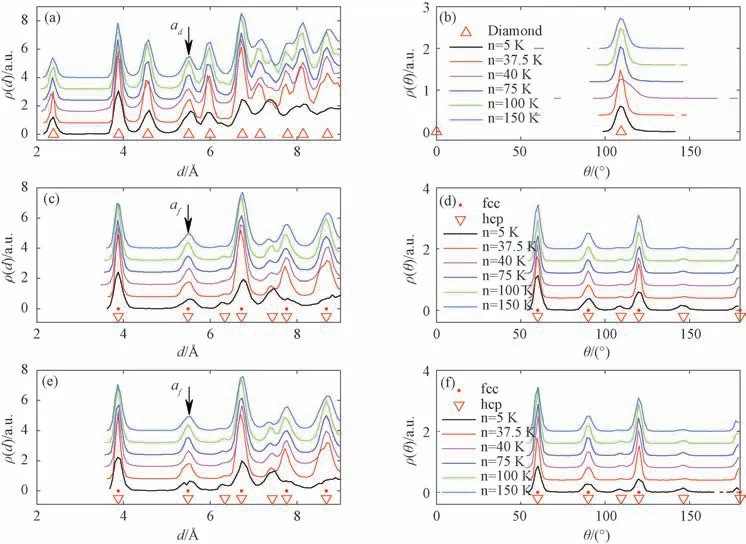
图6 低温时基于DL势得到的原子之间的距离ρ(d)和原子与其最近邻原子之间的角度ρ(θ)的分布函数(a)~(b)S1+S2 系统;(c)~(d)S1系统; (e)~(f)S2 系统Fig.6 Distribution functions of the distances between atoms and the angles between the lines linking one atom with its nearest neighborsρ(d)andρ(θ)with different temperature steps n applied at low temperatures for DL potential(a)-(b)S1+S2 system;(c)-(d)S1 subsystem; (e)-(f)S2 subsystem
当n=5 K 时,与其他冷却速率相比,S1和S2子系统均出现第三个d峰和θ=109.5°峰共存,显示出hcp晶格(图6)。但当温度步长增加时,S1和S2子系统中也有许多结构显示fcc晶格。例如,n=40 K时,在加热过程中,有一个fcc相向hcp相的转变(图5(a))。因此,并非所有模拟系统显示hcp晶格,而是同时存在fcc和hcp晶格。
图7显示了DL势在n=40 K 和T=50 K 时系统的原子排列。S1和S2的Si原子分别用黑色和绿色点表示,虚线框内展示的是ABAB…原子排列,而点线框内展示的是ABCABC…原子排列。Fcc点阵的原子排列是ABCABC…,而hcp点阵是ABAB…排列,其中A,B和C是密堆积的原子层,如图7中的虚线圈所示。在n=100 K时,模拟系统主要是金刚石结构(图5和6),晶化温度(液相转变为晶体相的温度)为1 602 K,晶格常数为5.209Å,与实验值1 687 K和5.430Å比较吻合[30]。
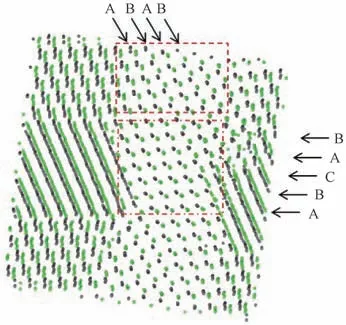
图7 在n=40 K 和T=50 K 时基于DL势得到的原子排列Fig.7 Atomic configurations for the system at n=40 K and T=50 K for DL potential
总之,应用DL 势的系统在冷却速率非常慢时得到纤锌矿结构,而冷却速率较快时得到金刚石结构。如果应用基态为fcc晶格的原子间势,则会形成金刚石结构。
3.3 DL模型与实验结果的比较
表2列出了在分子动力学模拟中应用不同原子间作用势获得的结晶温度,晶格常数和弹性常数。结果表明,晶体结构应该是原子间相会作用势有效性测试的第一个标准,只有基于DL 势的模拟才能得到金刚石结构;对于其他势,不能形成金刚石结构。另外,对于DL势,弹性常数c11约比实验数据大13%,并且c12=c44。与其他势的结果对比,DL 势模拟结果与实验数据之间的一致性证明了DL势的有效性。
目前,LJ势已广泛用于分子动力学模拟中,大多数研究人员认为LJ势仅适用于稀有气体或密堆积原子系统[22-23,30]。之前的研究表明,一个LJ势能仅得到hcp或fcc晶格,而不能得到其他晶格结构,例如体心立方(bcc)晶格[24]。然而在不设置任何初始布拉格点阵情况下,通过对LJ势的组合,可以获得金刚石结构和石墨结构[25]、CsCl(NaCl)结构和钙钛矿(ABO3)结构[26],这表明LJ势在构造原子间相互作用势中具有重要意义。
Tersoff和EDI势引入了三体势来定义键角,并在分子动力学模拟中形成109.5°的键角(如图2(b)所示)。但遗憾的是,引入三体势并没有获得金刚石结构;同样,COMB势即使考虑了电荷因素,也无法得到金刚石结构。
在基于DL势的分子动力学模拟中得到金刚石结构必须满足三个条件:首先,必须创建两种类型的原子,即使它们在物理上彼此相同;其次,这两种类型的原子必须具有各自的子点阵,在这里S1和S2原子可以显示hcp晶格或fcc晶格;第三,S1和S2原子之间的距离决定了所得的晶体结构。如果S1(S2)原子的最短距离是dA,S1和S2原子之间的最短距离是dAB,当dA/dAB之比在1.2~1.3的范围内时,可得到CsCl结构;dA/dAB之比在1.3~1.6范围内,可得到NaCl结构;dA/dAB之比在1.7~1.9之间得到金刚石结构;dA/dAB之比在1.9~2.1之间得到石墨结构。对于石墨结构,S1和S2原子可能显示hcp或fcc晶格,分别可得到α-石墨或β-石墨,每个单层对应石墨烯结构。
有趣的是,基于LJ势的分子动力学模拟中,即使基态对应于hcp晶格,当S1和S2原子之间的距离发生变化时,子系统的晶格也可以自适应以形成有序结构。对于CsCl结构,子晶格是dA/dAB=1.2 的简单立方(sc)晶格;对于NaCl结构,子晶格是dA/dAB=1.4的fcc晶格,这意味着在基于LJ势的分子动力学模拟中,系统可以自适应以形成能量上最低的有序结构。
4 结 论
本研究提出了适用于Si原子的分子动力学模拟的DL势,并测试了DL 势和其他作用势的有效性。DL势将LJ势进行组合为两个fcc晶格原子间势和两个晶格之间的原子间势来描述晶体结构。在不设置任何初始布拉格点阵情况下模拟Si的晶化过程,计算模拟系统中原子之间的距离和原子与其最近邻原子之间的角度的分布函数进行晶格识别。结果表明,只有应用DL势的模拟系统才能获得金刚石结构。通过应用DL势的模拟得到的晶化温度、晶格常数和弹性常数结果与实验数据相吻合。

