基于改进人工蜂群的高精度纵波慢度提取方法
陈立雄,董兴蒙
(1.中国石油集团测井有限公司天津分公司,天津 300280;2.中国电子科技集团公司第二十二研究所,河南 新乡 453000)
0 引 言
自从出现长源距声波测井以来,研究人员已经提出许多测井声波慢度处理方法,如小波变换法[1]、长短窗长比值法[2]、波形相干叠加法[3]等。其中,小波变换法和长短窗长比值法是对单道波形本身进行研究,对噪声比较敏感,当声波信号噪音干扰比较严重时,难以准确提取波形的慢度值。波形相干叠加法分为波形相似法[4]和n次方根法[5],其慢度值是对多维波形的全局特点进行研究,具有抗噪能力强、可靠性高的特点,在纵波慢度实时处理和阵列声波综合解释方面应用广泛。
随着油气勘探开发复杂程度逐年增高,油气勘探对声波测井提出了更高的要求。测井公司亟需对声波测井曲线进行高精度处理,以满足薄层、薄互层以及厚层细分的精细评价需求[6]。Tang等[7]基于波形相似法和声波测井深度组合处理技术实现了高分辨率慢度提取的目的。Ishikura等[8]通过全波形反演方法来提高声波测井慢度提取的精度,但是对于空间域采样严重不足的声波数据而言,上述方法由于相关性不足而导致精度下降。为了解决这个问题,李鹤升[9]探讨不同插值方法对声波测井慢度精度的影响。苏远大等[10]将频率—波数域相关滤波方法应用到数字声波慢度提取过程,通过改善地层纵波的相关性来提高慢度分辨率。上述方法技术难点多,计算复杂,并不适合纵波慢度的实时提取。郎晓政等[11]采用首波初至法计算声波测井的慢度,计算速度快,能够满足纵波慢度的实时提取,但是对波形的信噪比要求较高。
本文在李鹤升[9]研究的基础上,通过使用n次方根法和Akima 插值法提高实时测井中纵波慢度的精度。同时,为了降低慢度提取过程中的计算量,将改进的人工蜂群优化(Improved Artificial Bee Colony,IABC)算法与n次方根算法相结合,利用n次方根算法定义的相关函数作为适应度函数,通过智能算法的全局寻优特性获得最佳慢度值。与传统n次方根算法相比,本文所提的方法摆脱了时间步长和慢度步长的限制,能够有效提升纵波慢度实时提取的计算效率。
1 高精度慢度提取方法
1.1 n次方根法
n次方根法是Mcfadden等[12]在1986年提出的一种适用于多通道信号的非线性滤波方法,其定义的相关函数ρ(s,T)为
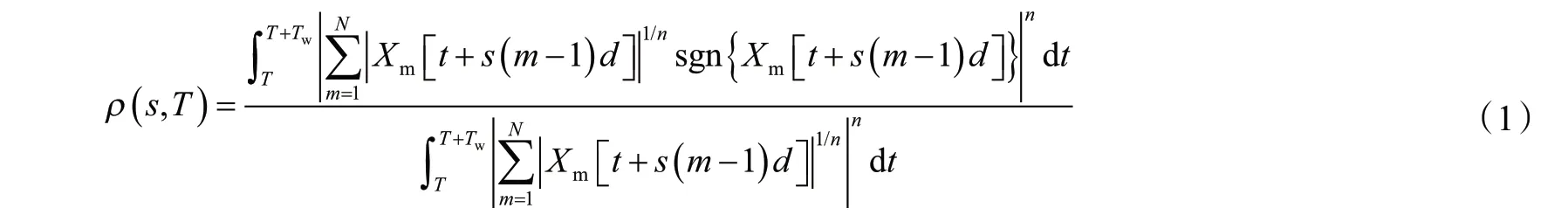
式中,sgn为符号函数;Xm(t)为N个接收换能器阵列中的第m个接收器数据向量;t为声波到时;T为起始数据点;Tw为数据的时间窗长,s;d为接收器之间的间距,m;s为声波慢度,s/m。
n次方根法属于纯粹数学运算,该方法利用指数n对波的振幅取n次方根将其缩幅,将缩幅后的数据进行叠加,再把叠加后的结果取n次幂方进行放大。在慢度提取的过程中,波形中波峰和波谷的振幅相对于其余部分保持不变,因而相干叠加后的相关函数峰值变得更尖锐,有助于慢度精度的提高。
图1给出了波形相似法(红线)和n次方根法(蓝线)的相关图,以及利用这2种方法计算得到的相关系数。通过对比两者封闭曲线的面积和相关系数值,可以看出利用n次方根法计算的结果更加精确。

图1 n次方根法与波形相似法对比
1.2 Akima 插值法
由于复杂地层中声速变化剧烈,并存在界面反射波叠加干扰的情况,声波测井仪的不同接收器在纵波波形幅度上具有明显差异,进而导致波形的相干性很差,使得慢度提取的精度降低。为了消除这类情况对慢度的干扰,采用Akima 插值法对声波测井的现场数据波形进行重采样。
Akima 插值法是一种五点求导分段三次多项式插值算法,用于二维平面曲线的插值与平滑[13]。该算法利用三次多项式在每2个数据点间拟合出1条曲线,最终由这些曲线连接而成的总曲线保证一阶导数连续。
给定D个不等间距样本点(ui,vi)(i= 0,1,…,D-1),u0<u1<…<uD-1,若在区间[ui,ui+1]上的2个端点满足式(2)。

则在任意2个邻近点(ui,vi)和(ui+1,vi+1)之间,可以确定唯一的三次多项式[见式 (3) ],三次多项式的系数a0、a1、a2和a4计算方法为式(4)。

其中,gi为(ui,vi)和(ui+1,vi+1)之间线段的斜率,其计算公式为式 (5),则(ui,vi)点处的切线斜率hi为式 (6)。

图2为数字声波实际测井数据在Akima插值前后的实际波形和慢度对比。从图2中可以看出,插值后的纵波波形一致性得到一定程度的改善,波形在部分相位处的幅值也有明显改善,因而Akima插值法对慢度精度的提高有一定帮助。

图2 Akima插值前后实际波形和慢度对比
2 基于改进人工蜂群的慢度提取方法
考虑到纵波慢度实时提取对算法高效性的要求,将人工蜂群(Artificial Bee Colony,ABC)算法引入到n次方根的慢度计算中,通过克服时间步长和慢度步长的限制降低了算法的计算量。此外,为了加快人工蜂群算法的收敛速度和提高全局寻优能力,本文在人工蜂群算法的搜索阶段进行改进,实现收敛速度和收敛精度的动态平衡。
2.1 人工蜂群优化算法
ABC算法是一种可用于解决多维多峰优化问题的智能算法,具有结构简单、调节参数少以及收敛速度快等特点[14]。ABC算法分为雇佣蜂、跟随蜂和侦察蜂这3个种群。3个种群的蜜蜂通过分工协作实现最优蜜源的寻找和开采。ABC算法搜索蜜源位置的阶段对应优化问题的寻优过程,蜜源的质量则通过优化问题的适应度值衡量。
ABC算法的整个流程分为初始阶段、搜索阶段和选择阶段。在初始阶段,人工蜂群算法随机产生初始可行解。

式中,sij为蜜源位置,j∈{1 , 2, ···,D}为D维解向量的分量;smax,j和smin,j分别为当前维度的最大值和最小值;r0为[0,1]的随机数。
在搜索阶段,雇佣蜂或侦察蜂在当前解的邻域内创造一个新解,并对跟随蜂的当前蜜源位置进行更新。

式中,k为蜂群发现的第k个蜜源,i、k∈{1 , 2, ··· ,N};yij为邻域内搜索得到的新蜜源位置;skj为邻域内随机选择的蜜源位置;r1为[-1,1]的随机数。
在选择阶段,跟随蜂采用轮盘赌方式对蜜源进行选择,其概率计算公式为
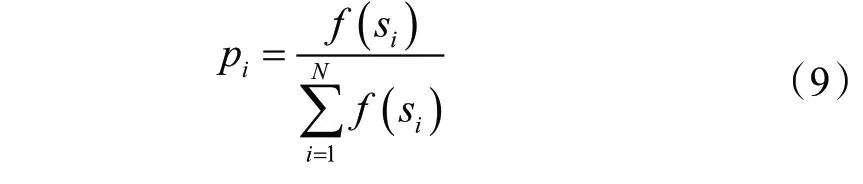
式中,f(si)为第i个蜜源的适应度值;pi为蜜源对应的概率,其值越大,被选择的机率越大。
2.2 改进的人工蜂群算法
考虑到搜索阶段的雇佣蜂与跟随蜂都在所寻找蜜源的邻域内进行寻优,其搜索范围的局限性降低了算法全局搜索能力。为了提高ABC算法的收敛速度与全局寻优能力,本文提出了一种改进的人工蜂群算法,通过引入全局最优解和自适应惯性因子来改善人工蜂群算法的性能。
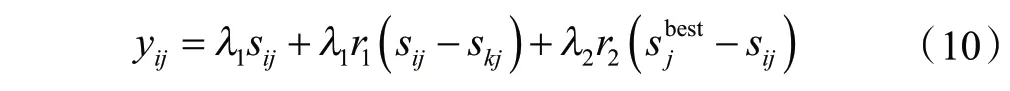
式中,r2为[0,1.5]上的随机数;为全局最优解的第j维值;λ1和λ2为自适应惯性因子,λ1和λ2定义见式(11)。
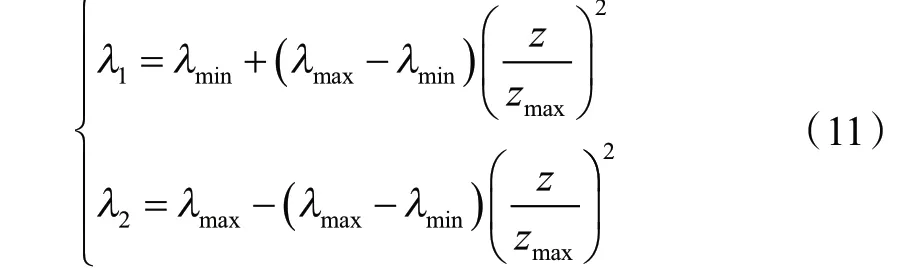
式中,z和zmax分别为当前迭代次数与最大迭代次数;λmax和λmin分别为惯性因子的最大值和最小值,本文取0.8和0.5。
通过上式发现,当z= 0时,λ1和λ2分别为惯性因子的最小值和最大值;当z=zmax时,λ1和λ2分别为惯性因子的最大值和最小值。这样设计的优势:在算法迭代早期,λ2的值较大,保证ABC算法能够以较快的速度寻找蜜源全局最优解,从而大幅提高收敛速度;随着迭代次数的增加,λ1逐渐增大,使得种群的多样性得以保证,从而跳出局部最小值,获得更高的收敛精度。
2.3 基于IABC算法的慢度提取
将IABC算法与n次方根算法相结合,用于优化n次方根的计算效率。设n次方根的相关函数为目标函数,人工蜂群算法中的蜜源表示给定时间区间和慢度区间内的相关值,蜂群根据适应度函数找寻最优蜜源即搜寻最优解。在慢度提取过程中,最优蜜源即真实慢度对应的最大相关值。基于IABC算法的慢度提取流程图见图3。
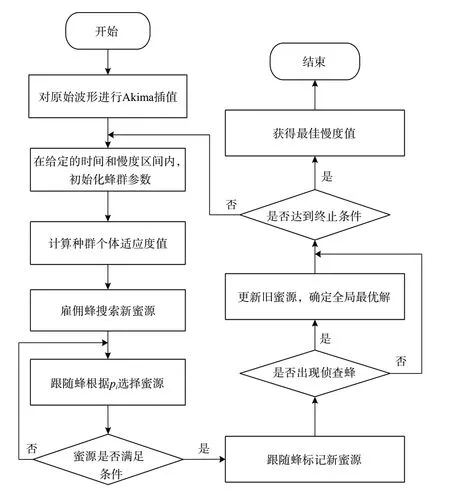
图3 基于IABC算法的慢度提取流程图
由于现场采集软件注重资料的实时处理能力,对算法的准确性和稳定性要求较高,需要对n次方根法和IABC算法的参数设置进行优化,保证算法能够满足现场解释的需求。对于n次方根法的参数,将n值设定为4;起始时间设定为噪声门;时间窗长设置为100 ~200 μs,需要根据现场的井眼和仪器因素动态调整;慢度区间设置为[s0-50,s0+50] μs/ft** 非法定计量单位,1 ft =12 in =0.304 8 m,s0表示前一个深度点的慢度值。对于IABC算法的参数,种群规模设置为100,最大迭代次数为40,最大开采度设置为1 000。
3 实际资料分析
选取大港油田A井的实际测井数据为测试数据,测试井段为4 150 ~4 200 m。数字声波测井仪的采样点数为256,采样间隔为2 μs。利用IABC算法和ECLIPS-5700软件分别对测试数据进行纵波慢度提取,并将测试曲线进行对比(见图4)。从图4中可见,相较于ECLIPS-5700软件对现场数据提取的慢度结果,基于IABC的纵波慢度提取方法的结果精度更高,慢度曲线对厚度约1 m的薄层具有较好的响应。
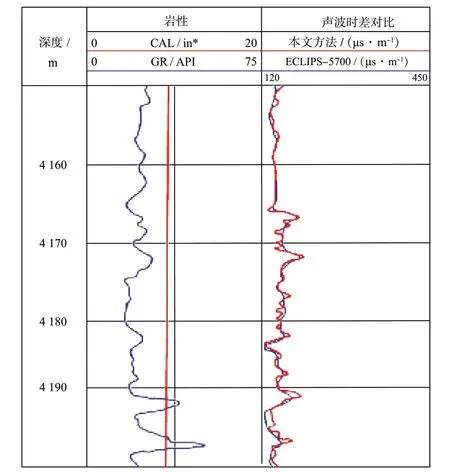
图4 大港油田A井纵波慢度曲线
实时采集处理方法不仅需要满足测井现场对纵波慢度精度的要求,还需要注意算法效率。利用同一口井的测井数据,对比基于IABC的纵波慢度提取方法与传统的慢度—时间相关(STC)方法在不同深度时的计算时间(见图5)。通过对比发现,由于n次方根复杂的计算量和Akima插值运算,使得本文方法在深度1 000 m以下的计算时间略大于STC方法。但是,随着深度的增加,本文方法的计算效率略有提升,计算时间略小于STC方法,这充分说明改进人工蜂群算法和参数设置能够在一定程度上优化计算速度,提升算法的性能。

图5 不同慢度提取算法的时间对比
4 结 论
(1)利用Akima 插值技术对声波测井波形进行重采样,能够改善地层纵波相关性,对地层纵波慢度精度的提高有一定的帮助。
(2)基于改进人工蜂群的n次方根慢度提取方法具备高精度、高效率和高稳定性的特点,能够满足测井现场对纵波慢度实时提取的要求。
(3)通过现场测井实验,该算法能够明显提高复杂地层井段的纵波慢度精度,清晰地刻画地层的薄互层特征。

