驱动端不对中对核心机单元体动平衡影响的理论研究

杨法立，刘 超，林大超，陈文超

(1.中国航发沈阳发动机研究所，辽宁 沈阳 110300；2.杭州集智机电股份有限公司，浙江 杭州 310000)

1 引 言

由高压压气机、燃烧室和高压涡轮组成的发动机核心机，是航空发动机研制的主要难点和关键技术最集中的部分[1]。核心机单元体的高压转子由压气机转子和高压涡轮转子组成，若高压转子残余不平衡量没有达到要求，在工作过程中会引起较大的机械振动，严重影响航空发动机的工作性能，直接影响航空发动机的使用寿命。尽管高压转子在加工装配过程中会采用各种技术手段减小转子的不平衡量[2]，并且严格按照设计要求完成多步平衡[3]，但在将高压转子装入机匣的过程中，还是会引入不平衡量。首先，核心机单元体的机匣包括中介机匣、高压压气机机匣、主燃烧室机匣、高压导向器机匣等，这些机匣的同轴度会影响高压转子的支承情况；其次，整体装配后引入了刚性或弹性支承，与高压转子单独做动平衡时的支承不同。因此，有必要在完成核心机单元体的整体装配后，在尽可能接近发动机真实工作状态下使用平衡机再做一次动平衡。

对核心机单元体的动平衡测试而言，为了保证测量精度及有效性，首先要对外界引入的不平衡量进行分析，而驱动端连接转子处的不对中所引入的不平衡成为不可忽视的一部分。本文对连接处不对中进行受力计算，使用ANSYS有限元分析软件对某型号核心机单元体及平衡机摆架进行一体化有限元建模，分析驱动端的不对中对核心机单元体动平衡测量带来的影响，为高精度动平衡提供理论依据。

2 不对中动力学计算

本文研究的核心机单元体的转子与驱动主轴端之间使用万向联轴器连接，如图1所示。两构件不对中一般分为平行不对中和偏角不对中。对于本文所研究的万向联轴器，平行不对中和偏角不对中是同时存在的，下面分别对这两种不对中情况进行力学分析。

图1 万向联轴器

2.1 平行不对中力学分析

一般情况下，图2所示的平行不对中坐标系可以表示出两个连接的单元体(单元体1和单元体2)在平行不对中状态下的力及力矩的情况[4]。平行不对中包括在x轴方向的不对中和y轴方向的不对中。

图2 平行不对中坐标系

可以将驱动端和转子端沿轴线方向投影，形成图3所示的联轴器不对中受力模型。图3中，O1和O2分别为驱动端输出轴和转子轴的旋转中心，P点是可以视为连接处上的螺栓连接点，ΔE是可视为将不对中全转化在y状态下的不对中度，ω为连接处在不对中旋转方向上旋转速度，R是旋转中心O1到连接点P的距离，r是旋转中心O2到连接点P的距离，Fx和Fy是作用在螺栓上连接点的力F在x轴和y轴方向的分力。

图3 平行不对中受力模型

在图3中，万向联轴器转动时，旋转半径R>r，万向联轴器的左右两端会发生变形，产生将驱动端和转子端往同轴心方向的拉力。在图3中，O2B垂直于O1P，因为实际中的不同心量很小，所以O2P的距离r远大于ΔE，因此可视为PB=r，两旋转半径的差值可视为O1B，即：

O1B=R-r=ΔEcosωt

(1)

又因万向联轴器左右两端为对称结构，可视为两端的变形量也相同，因此有单边的变形值d为O1B的一半，即：

(2)

设万向联轴器在O1P方向的刚度为kR，有：

(3)

沿x向和y向分解，可得：

(4)

(5)

从平行不对中条件下的受力计算式可以看出，在联轴器连接点处受到沿x向和y向的激振力，激振力频率与两倍转速相同，其大小与平行不对中度和径向刚度有关。本文所建立的摆架-核心机不平衡、不对中振动响应计算模型是线性的，即满足叠加性条件。式(4)和式(5)所示的不对中力或者是常数，或者是转速的二倍频简谐力，与工频的不平衡力无关。根据线性叠加原理，二者可以分别计算后再叠加，结果是一样的。也就是说，式(4)和式(5)所示的不对中力对不平衡响应没有影响。

2.2 偏角不对中力学分析

图4所示为偏角不对中情况下系统的受力模型[5]，T为驱动端的驱动扭矩。由于联轴器处的不对中可以分解成TZ和TR，其中TZ是沿转子中心轴方向的分量，因此有：

图4 偏角不对中受力模型

TR=Tsinα

(6)

TZ=Tcosα

(7)

其中，TZ沿转子轴线，弯矩TR垂直于TZ，弯矩TR在x轴和y轴方向的分量为Tx和Ty，对应关系如下：

Tx=Tsinαcosωt

(8)

Ty=Tsinαsinωt

(9)

两不对中的轴之间存在α夹角情况下的相对速比计算如下：

(10)

(11)

(12)

(13)

角度不对中引起的扭矩计算如下：

(14)

x和y方向的扭矩为：

(15)

(16)

综合上面的计算，引起的转子端面上不对中附加力(Fx，Fy，Fz)及附加力矩(Tx，Ty，Tz)汇总如下：

(17)

2.3 万向联轴器处不对中力学分析

对于本研究系统所使用的万向联轴器而言，由于万向联轴器在x轴、y轴方向可以自由活动，因此联轴器x轴、y轴的等效刚度Kx和Ky基本为0，由平行不对中带来的核心机转子上的附加力(Fxa，Fya，Fza)基本可以忽略，即在微小平行不对中情况下产生的附加力可以忽略，万向联轴器处微小平行不对中的影响可以忽略不计。但由于微小偏角不对中引起的附加力矩依然存在，该力矩作用在核心机转子的最左端，如图5所示。

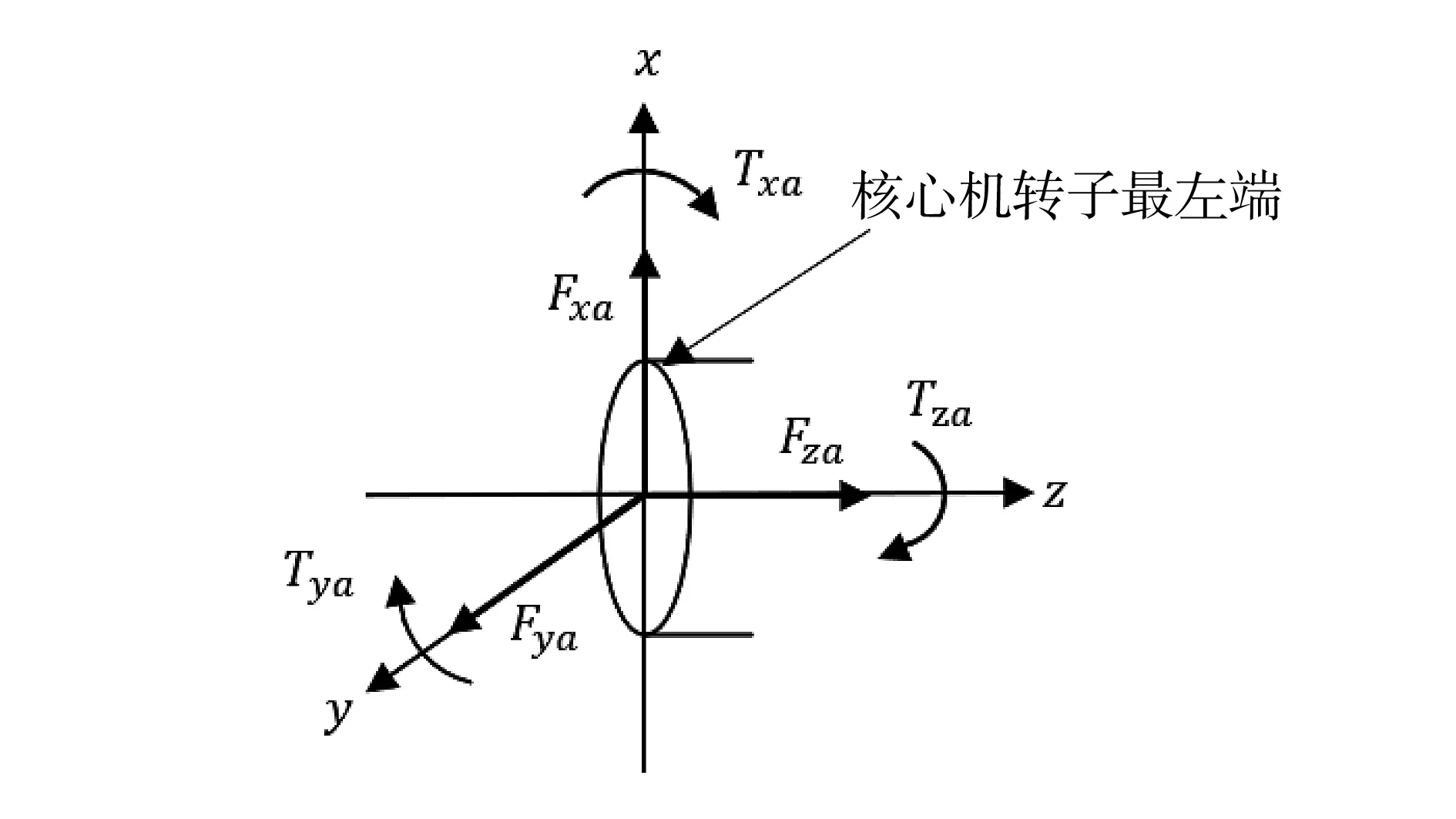
图5 核心机转子左端受力模型

由式(17)及已知条件可得：

Fxa=0,Fya=0,Fza=0

驱动端与核心机转子之间的偏角不对中α引起的核心机转子上的附加力矩Tza，Txa，Tya计算如下：

(18)

Txa=Tzatanαcosωt

(19)

Tya=Tzatanαsinωt

(20)

其中，Iza为核心机转子整体的极转动惯量，由已知的转子参数可知，Iza为8.39kg·m2。万向联轴器活动段截距为215mm,在偏角不对中α约为0.5°、1°、3°的情况下，计算出的参数如表1所示。

表1 计算参数

由表1可知，因为不对中偏角α很小，所以C2≪1。由三角函数公式可得：

(21)

(22)

由此可得：

Tx=IZtanα·2C1C2ω2sin2ωtcosωt=IZtanαC1C2ω2(sin3ωt+sinωt)

(23)

Ty=IZtanα·2C1C2ω2sin2ωtsinωt=IZtanαC1C2ω2(cos3ωt-cosωt)

(24)

由上面公式可知，当不对中偏角α很小时，会导致频率与转频一致的不对中振动响应，这部分振动与不平衡引起的振动混在一起，会对动平衡测试造成一定的影响。此外，还会引起频率为转频3倍的不对中振动响应，根据线性系统叠加原理，这部分振动独立于不平衡响应，不会对核心机单元体平衡测试精度造成影响。

3 系统有限元计算模型

本文所研究的系统包括平衡机摆架结构与核心机单元体，其中，核心机单元体由转子部分(高压压气机转子和高压涡轮转子)、轴承支承(球轴承和滚棒轴承)、静子部分(中介机匣、高压压气机机匣、主燃烧室机匣、高压导向器机匣等)构成。

对于此平衡机摆架-核心机单元体系统比较复杂的情况，如果直接用ANSYS还原整个系统的几何模型，不仅极大地增加了工作量，而且在进行网格划分及设立边界条件时会造成很大问题，极易产生错误，因此有必要对整个系统模型进行合理的简化。对于系统中使用螺栓或者其他配合进行刚性连接的部分，可以划分为统一整体进行建模。因此，摆架部分、转子部分及机匣静子部分可以各自简化为一个整体，使用ANSYS建立模型、划分网格及建立约束条件，系统整体ANSYS有限元模型如图6所示。

图6 系统整体ANSYS有限元模型

核心机单元体选择分析类型为Harmonic，边界条件在建模时已经确定，两轴承支承的刚度分别为5×107N/m和25×107N/m。由于该核心机单元体在动平衡设备上转子的测量转速为20Hz，所以设置仿真频率范围取值为0～25Hz。根据表1的计算参数，使用F指令在核心机单元体转子上施加力矩，转子受力云图如图7所示。计算求解提取出摆架上测量传感器位置处在20Hz转速下的幅值响应，所得结果见表2。

图7 转子受力云图

表2 摆架上测量传感器位置处的幅值响应

根据本研究对象核心机单元体的不平衡量要求，同样使用F指令在转子上施加合格不平衡量大小的不平衡力，进行谐响应分析，计算出在20Hz转速下平衡机摆架上测量传感器位置处的幅值响应，其结果为4.38×10-8m。与表2中的3种偏角不对中情况对比可知，在联轴器处的偏角不对中达到3°时，振幅响应的数量级才与之接近；在偏角不对中为0.5°、1°时，摆架上两个测量位置的响应值远小于合格不平衡量状态下的响应，对测量而言，其影响几乎可以忽略，这主要是因为在计算附加力矩时，C2及tanα值受偏角α的影响很大。

根据所研究对象核心机单元体的动平衡测试要求，在实际条件下，驱动端联轴器处安装不同心度不超过0.05mm，转化为偏角不对中约为0.013°，远远小于0.5°。可见，在现有的安装标准条件下，其驱动端的不对中对该核心机单元体动平衡测试的影响可以忽略。

4 结 论

本文通过建立平行不对中和偏角不对中受力模型，对所研究的万向联轴器处不对中给核心机单元体带来的影响进行理论计算分析，同时配合使用ANSYS有限元分析软件对核心机单元体及平衡机摆架进行一体化有限元建模。通过对计算结果的分析发现，在线性系统假设下，不对中有可能引起工频、2倍频和3倍频等振动响应。其中，工频振动与摆架测量不平衡响应频率一致，有可能影响动平衡测量精度；2倍频和3倍频等高阶倍频不对中振动响应，理论上不影响动平衡测量精度。对于本试验研究的核心机单元体在平衡机摆架上的动平衡测试而言，在驱动端联轴器的安装要求为不同心度不超过0.05mm的状态下，由不对中带来的影响对此动平衡测量几乎可以忽略，即现有的标准下核心机单元体的动平衡可以正常进行。