整体径向传输线谐振特性分析

周 全，邹晓兵，王新新

(1. 清华大学 电机工程和应用电子技术系，北京 100084；2. 国防科技大学 前沿交叉学科学院，长沙 410005)

1997年，Z箍缩研究取得了突破性进展[1]。据估计，当Z箍缩装置的驱动电流达到60 MA时可望实现聚变点火[2]。然而，现阶段世界上最大的Z箍缩驱动源为美国的Z Refurbishment(ZR)装置，电流峰值仅为26 MA。近些年，各国纷纷提出了一系列新型Z箍缩装置的概念设计，如美国圣地亚国家实验室提出的Z-800装置[3]及我国提出的CZ-30装置[4]等。在这些设计中，通常采用整体径向传输线(monolithic radial transmission line, MRTL)将许多脉冲发生器产生的脉冲汇聚并传输至负载。为实现阻抗匹配，MRTL一般为非均匀传输线，波阻抗沿传输方向单调变化。

以往对于MRTL的研究大多采用电路仿真模型，将其等效为足够多段的均匀传输线的级联[5-9]。电路仿真结果显示MRTL具有高通特性，这一特性有利于缩短主脉冲上升沿。然而，电路仿真的基本假设是电磁波以准TEM模式传播。Z箍缩装置中使用的MRTL尺寸巨大、结构复杂，准TEM假设需进行验证。2008年，Welch等[10]对MRTL进行了2维电磁场模拟，发现2维电磁场仿真结果与电路仿真结果基本相同。2015年，毛重阳等[11]对MRTL进行了3维电磁场时域仿真，发现MRTL的最大功率传输效率比电路仿真结果低约15%，表明准TEM模假设对Z箍缩装置中使用的MRTL并不成立。2019年，本文作者团队[12]构建了完整Z箍缩装置的仿真模型，仿真结果表明，与MRTL电路模型相比，采用3维电磁场模型时，负载电流幅值更低且上升时间更长，该研究进一步说明准TEM假设对Z箍缩中的MRTL并不成立，研究MRTL时应采用3维电磁场模型。

2020年，本文作者团队[13]首次利用3维电磁场模型获得了MRTL的频域传输效率曲线，并发现了MRTL的谐振频率现象，即由于非TEM模的存在，MRTL并不呈现以往电路仿真中得到的高通特性，反而非TEM模谐振将在高频段造成一系列传输效率接近0的特殊频率点。由于MRTL内非TEM模不可忽略这一现象发现时间较近，且MRTL结构复杂、尺寸巨大，3维电磁场仿真分析难度大、耗时长，目前并未有其他学者利用3维电磁场模型对MRTL传输特性进行分析。

然而，上述研究只是提出了谐振频率现象，并未深入研究MRTL谐振频率的影响因素。研究谐振频率的影响因素对MRTL的设计和使用具有重要的实践指导意义，可使MRTL的工作频率远离这些谐振频率点。根据电磁场模型，众多因素都可能对谐振频率存在影响，部分因素的影响可通过理论计算公式进行分析，而理论计算公式中未考虑的因素包括输入结构、线型和挖孔设计。因此，本文首先从谐振频率的理论计算公式出发，分析公式所包含因素对谐振频率大小的影响，接着分析上述剩余3个变化因素的影响。

1 理论计算公式中的影响因素

由于分析谐振频率大小影响因素的意义在于指导MRTL的设计和使用，使MRTL的谐振频率远离其工作频率范围，因此本文重点关注第一个谐振频率点的变化。第一个谐振频率点为所有谐振频率点中频率最低的[13]，只要第一个谐振频率点的频率大于MRTL最大工作频率，那么所有谐振频率点都不处于MRTL的工作频率范围内，谐振频率现象就不会影响MRTL工作时的传输性能。对于Z箍缩，其电流脉冲上升时间在百纳秒量级。图1为MRTL输入脉冲等效波形及对应的频谱。由图1可见，输入脉冲的频域分量主要集中在0～10 MHz。因此，第一个谐振点的频率需大于10 MHz。

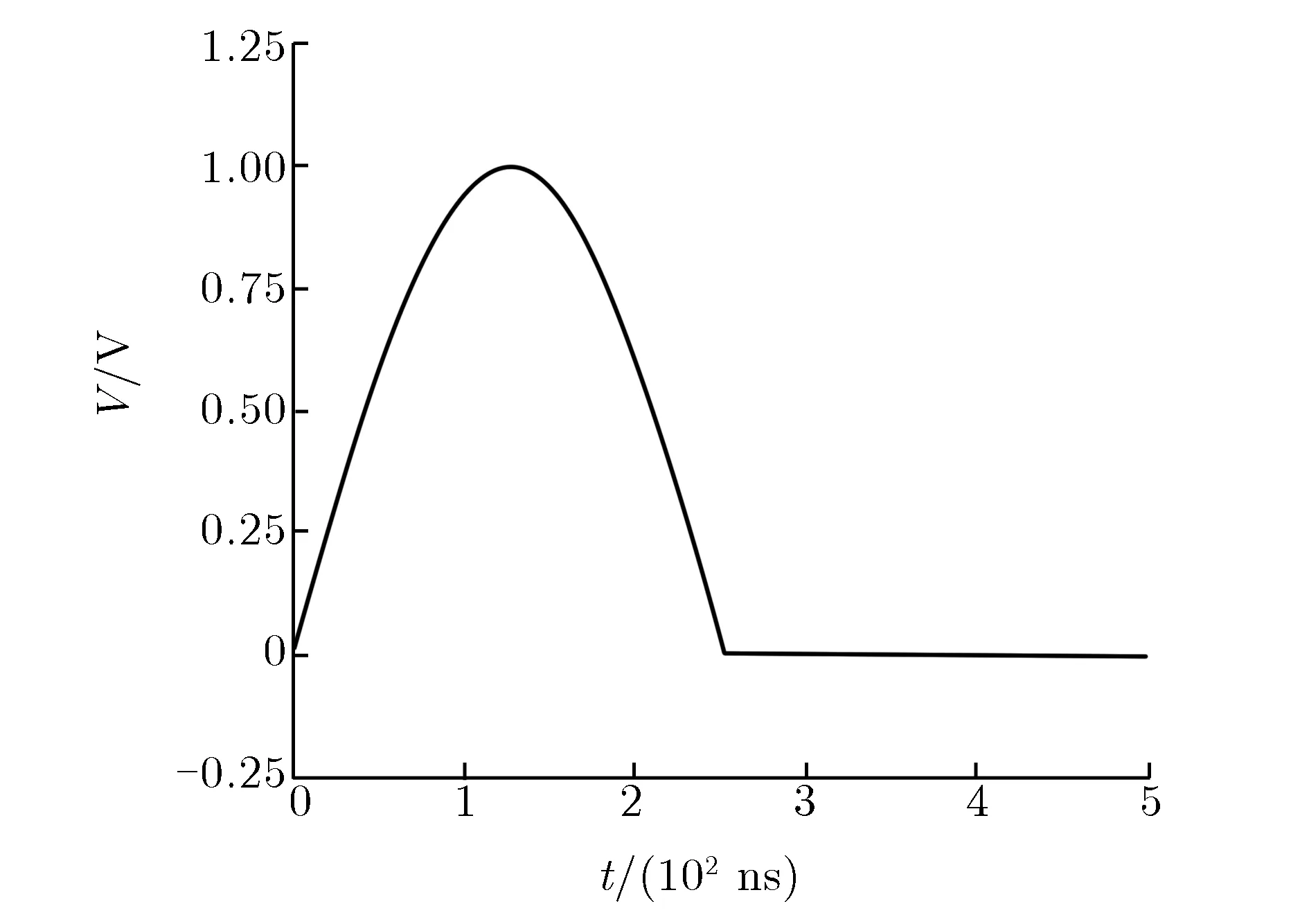
(a) Waveform

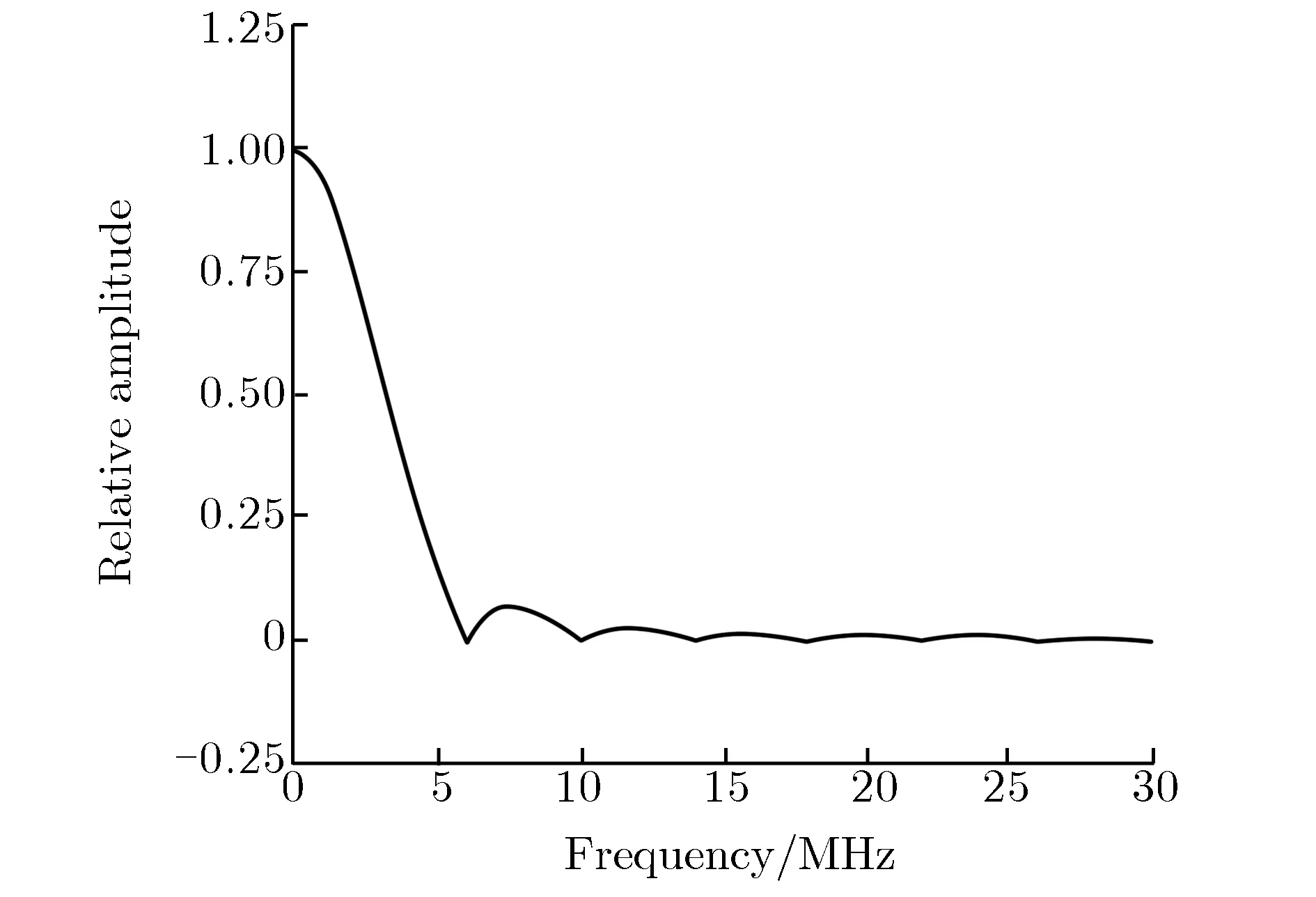
(b) Spectrum

研究表明，MRTL谐振频率可由磁壁模型计算[13]，表示为

(1)

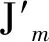
式(1)中存在的变量有贝塞尔函数的阶数m、外圈半径ri、内圈半径ro、绝缘介质的相对介电常数εr和相对磁导率μr。由于MRTL内圈一般与磁绝缘线相连，内径很小且可变范围不大，因此本文不考虑内圈半径ro对谐振频率大小的影响。常规绝缘介质的相对磁导率μr一般为1，因此也不考虑μr的影响。从前文的分析可知贝塞尔函数的阶数m是输入同轴线数N的整数倍，因此分析贝塞尔函数的阶数对谐振频率大小的影响，其实就是分析输入同轴线数对谐振频率大小的影响。综上，对式(1)中出现的变量，本文仅讨论输入同轴线数N、外圈半径ri和绝缘介质的相对介电常数εr对谐振频率大小的影响，下面将对这些变量一一进行理论分析和电磁场模拟研究，仍使用Z-800装置中的MRTL为仿真案例。

1.1 输入同轴线数

对一个输入同轴线数为N的MRTL，其谐振模式为TEm,n,0，其中，m为N的正整数倍，n为正整数。当N变化时，谐振模式也将变化，即式(1)第一个方程的解k将会变化。根据文献中给出的磁壁模型的模式图[14]，当n相同时，贝塞尔函数的阶数m越大则k解越大。因此，对第一个谐振模式TEN,1,0，N越大则k越大，进而f越大，即谐振频率大小和N成正相关。为验证这一分析，建立不同N下MRTL的3维电磁场模型，除N外其余参数都不变，仿真得到前3个谐振频率及对应的谐振模式，如表1所列。由表1可知，随着N的增大，虽然谐振模式不同，但第一个谐振频率在变大。其余位于同一次序的谐振模式由于n值相同，因此谐振频率也随着N的增大而增大。为使谐振频率规避Z箍缩电流所在的主频范围，输入同轴线数应大于22。

表1 改变MRTL输入同轴线数后谐振频率仿真值对比Tab.1 Comparison of the resonant frequencies after changing the number of MRTL inputs

1.2 外圈半径

当外圈半径ri变化时，MRTL内的谐振模式并不改变，只是对应的谐振频率大小发生变化。对MRTL而言，ro/ri很小，因此，为简化分析，认为当ri变化时，ro/ri近似不变。那么，对某一谐振模式，式(1)第一个方程的解k近似不变。由k的表达式可知，为保证k不变，当ri增加时f应减少。因此，对任一确定的谐振模式，ri与对应的谐振频率呈负相关。为验证这一分析，建立不同ri下MRTL的3维电磁场模型，除ri外其余参数都不变，仿真得到前3个谐振频率及对应的谐振模式，如表2所列。由表2可知，随着ri的增大，同一个谐振模式对应的谐振频率在减少。对需重点关注的第一个谐振频率，随着ri的增加而减少。为使谐振频率规避Z箍缩电流所在的主频范围，MRTL外圈半径应小于17.5 m。

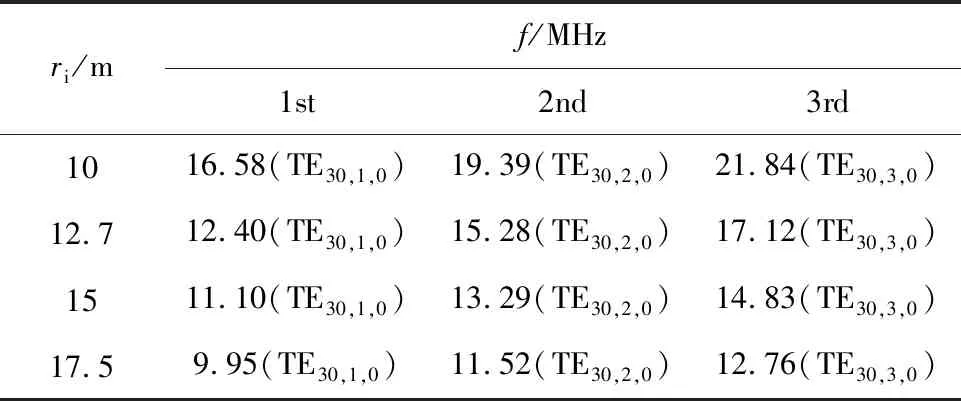
表2 改变MRTL外圈半径后谐振频率仿真值对比Tab.2 Comparison of the resonant frequencies after changing the outer radius of MRTL

1.3 绝缘介质相对介电常数

与外圈半径变化时的分析类似，当绝缘介质的相对介电常数εr变化时，MRTL内的谐振模式不变，且k解不变。由k的表达式可知，对任一确定的谐振模式，εr与对应的谐振频率呈负相关。为验证这一分析，建立采用不同εr的绝缘介质时MRTL的3维电磁场模型，除εr外其余参数都不变，仿真得到前3个谐振频率以及对应的谐振模式，如表3所列。

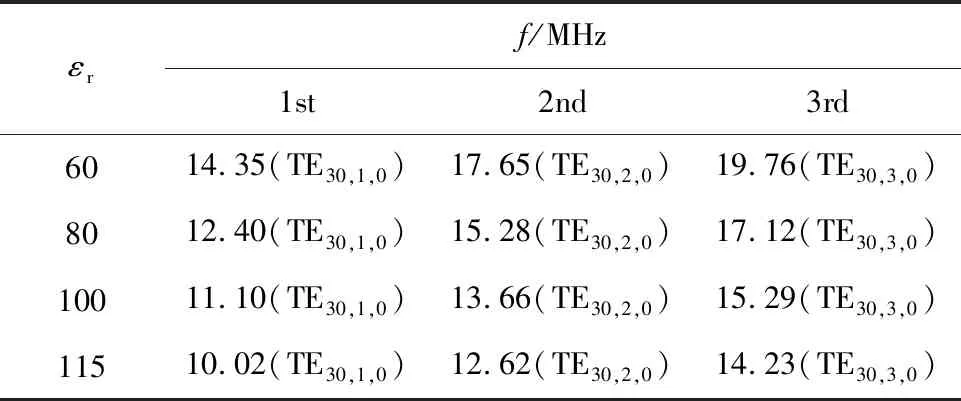
表3 改变绝缘介质相对介电常数后谐振频率仿真值对比Tab.3 Comparison of the resonant frequencies after changing the relative permittivity of insulating medium

由表3可知，随着绝缘介质εr的增加，同一个谐振模式对应的谐振频率在减少。需重点关注的是，第一个谐振频率随着绝缘介质εr的增加而减少。为使谐振频率规避Z箍缩电流所在的主频范围，绝缘介质相对介电常数应小于115。

上述因素对谐振频率的影响也可通过谐振频率形成的物理机制进行定性认识。对于第一个谐振频率点，对应的波长约等于MRTL外圆周上相邻脉冲源间的角向距离[13]。因此，输入同轴线数越大，相邻脉冲源间的角向距离越小，对应的第一个谐振频率越大；外圈半径越大则相邻脉冲源间的角向距离越大，对应的第一个谐振频率越小；绝缘介质相对介电常数增大时，虽相邻脉冲源间的角向距离不变，但由于波速变慢，因此，对应的第一个谐振频率减少。可见，通过物理机制的分析，同样可得到输入同轴线数与谐振频率大小成正相关，外圈半径和绝缘介质相对介电常数与谐振频率大小成负相关。

从理论计算公式出发，分析了上述因素对谐振频率的影响后，下面将讨论输入结构、线型和挖孔设计等理论计算公式中未考虑的因素对谐振频率的影响。

2 剩余影响因素

2.1 输入结构

根据式(1)得到的Z-800装置谐振频率理论值与3维电磁场模拟得到的仿真值的对比，如表4所列。

表4 Z-800装置谐振频率理论值与仿真值对比Tab.4 Comparison between theoretical value and simulation value of resonant frequencies of Z-800 facility

由表4可知，谐振频率仿真值都小于理论值。这是由MRTL和输入同轴线连接处的转换结构造成的。图2为MRTL和输入同轴线连接处的转换结构。与波长相比，同轴线内导体相对外导体的额外长度较小，因此可忽略其影响，仅考虑同轴线内外导体表面电场的影响。根据微波理论，同轴线内外导体上垂直表面的电场可等效为一个并联电容[14]，因此输入端转换结构的电磁场最终等效为一个并联电容。在谐振频率点，输入端的电压幅值最大，因此MRTL内的谐振可视为并联谐振。输入端转换结构等效的并联电容相当于增加了这个谐振系统的电容，因而降低了谐振频率。

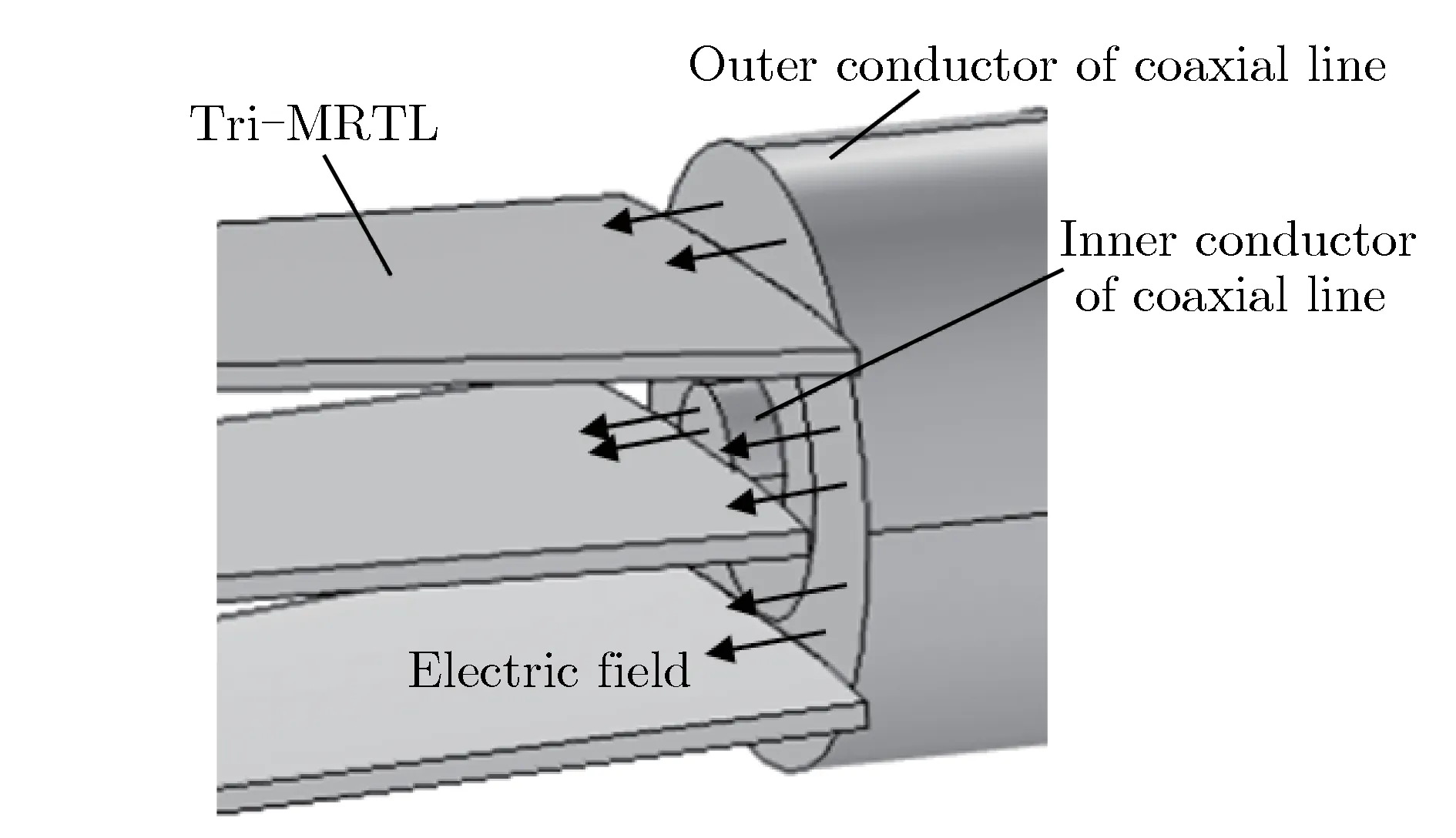
图2 MRTL和输入同轴线连接处的转换结构Fig.2 Input structure at the junction of MRTL and input coaxial line

为验证这一猜测，本文将输入同轴线外导体的厚度由Z-800装置设计的0.6 m减少为0.05 m。在减少同轴线外导体厚度后，由外导体表面电场带来的影响范围缩小，输入端转换结构处等效的电容值减少，因此，谐振频率的3维电磁场仿真值应更接近磁壁模型得到的理论值。表5为减少外导体厚度后，前3个谐振频率及其谐振模式的仿真值和理论值对比。由表5可知，前3个谐振频率对应的谐振模式仍相同，且谐振频率理论值和仿真值的相对偏差变小。

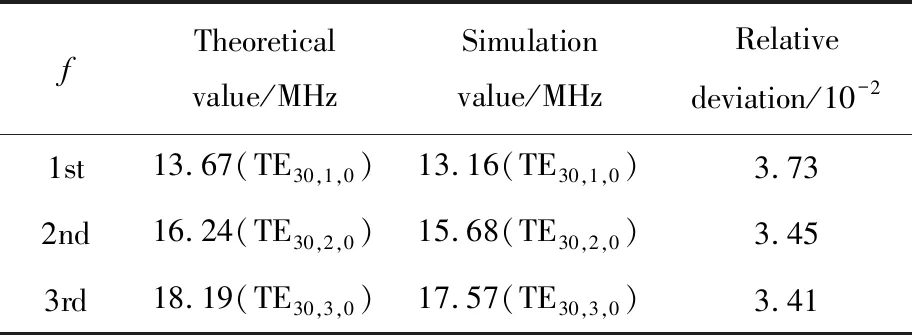
表5 减少同轴线外导体厚度后Z-800装置谐振频率理论值与仿真值对比Tab.5 Comparison between theoretical value and simulation value of resonant frequencies of Z-800 after reducing the thickness of the outer conductor of the input coaxial line

2.2 线型

Z箍缩装置中常用的MRTL线型有线性线、指数线和双曲线。Z-800装置中使用指数线型。不同线型MRTL的区别在于阻抗变化规律，线性线、指数线和双曲线的波阻抗分别沿着径向位置呈线性、指数和双曲线规律变化。阻抗变化反映在几何结构上则是极板间距随径向位置的变化规律不同。图3为不同线型MRTL极板间距h(r)随径向位置r的变化关系。

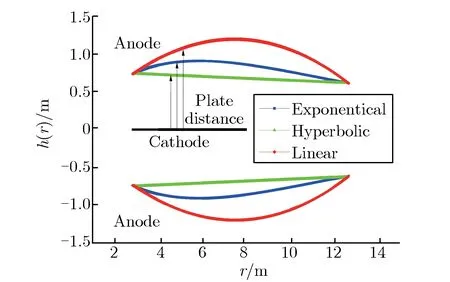
图3 不同线型MRTL极板间距随径向位置的变化关系Fig.3 h(r) vs. r in different line type of MRTLs

为分析MRTL线型对谐振频率大小的影响，本文分别建立了不同线型MRTL的3维电磁场模型，通过频域仿真得到了前3个谐振频率及对应的谐振模式，如表6所列。

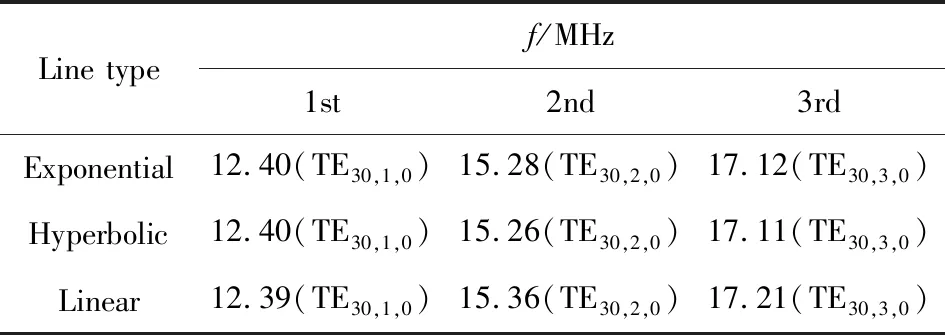
表6 不同线型MRTL的第一个谐振频率对比Tab.6 Comparison of the first resonant frequency in different type line of MRTLs

由表6可知，不同线型MRTL的谐振频率大小基本相同，即线型对谐振频率大小基本没有影响。这是因为不同线型MRTL的区别在于极板间距，而引起谐振现象的原因是角向电流，与极板间距变化无关。此外，极板间距变化造成的非TEM模可忽略，这在对MRTL的2维电磁场仿真中已得到证明[7]，因此，不同极板间距的MRTL都可等效为平板电极的磁壁模型，可利用磁壁模型估算谐振频率。鉴于此，MRTL线型对谐振频率基本没有影响。

2.3 挖孔设计

第2.2节讨论的MRTL的极板都是完整的，依靠极板间距变化实现不同的线型。对Z-800装置所用的指数三板MRTL而言，为实现极板间距的变化规律，中间极板为平面，上下极板为曲面。然而，在实际应用中，为便于多个MRTL叠放，希望MRTL上下极板也是平面。因此，挖孔设计MRTL被提出。在挖孔设计中，MRTL的极板都为平面，为达到希望的线型，会在相邻输入端间挖孔。挖孔后，MRTL波阻抗可表示为

(2)

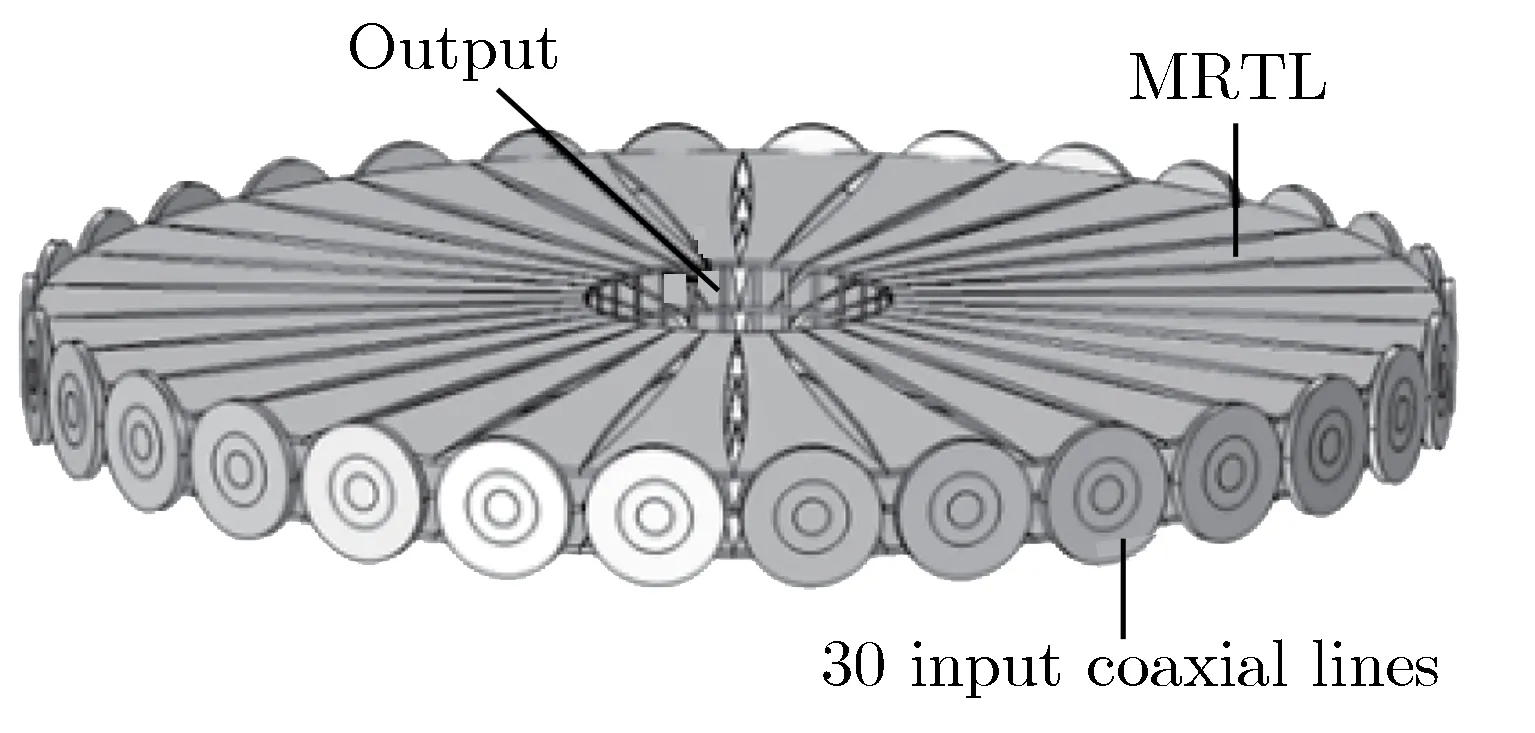
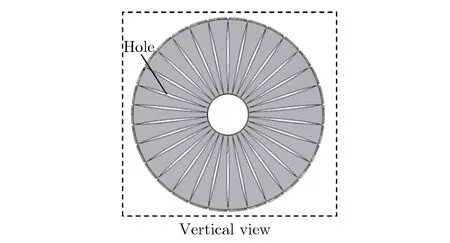
其中，θ(r)为极板在径向位置r处对应的圆心角。通过改变挖孔面积的大小，进而改变θ(r)，这样就算使用平板电极，也可实现不同的线型。对于Z-800使用的指数线，挖孔设计的MRTL结构如图4所示。

(a) Waveform

(b) Spectrum

本文建立图4挖孔设计MRTL结构的3维电磁场模型，频域仿真得到的挖孔和非挖孔设计MRTL的传输效率S21随谐振频率的变化关系如图5所示。

图5 挖孔和非挖孔设计MRTL的传输效率S21随谐振频率的变化关系Fig.5 S21 of the MRTL with and without digging holes vs. f

由图5可见，与非挖孔设计MRTL类似，挖孔设计MRTL的S21曲线上同样存在一系列传输效率接近0的特殊频率点。通过观察挖孔设计MRTL工作在每个特殊频率的电磁场时空分布可见，挖孔设计MRTL在每个特殊频率点也发生了谐振。挖孔设计和非挖孔设计MRTL的前3个谐振频率和对应的谐振模式如表7所列。

表7 挖孔设计和非挖孔设计MRTL的前3个谐振频率和对应的谐振模式对比Tab.7 Comparison of the first three resonant frequency of the MRTL with and without digging holes

由表7可知，挖孔设计MRTL的谐振模式与不挖孔MRTL的谐振模式相同，且对应的谐振频率十分接近。这是因为，对于MRTL的任一谐振频率，相邻输入端的中间部分都是电荷聚集区，也就是电压幅值最大点。谐振时，电流是在相邻的电压幅值最大点间流动。由于挖孔部分即是在相邻输入端的中间部分，所以挖孔部分在谐振模式下是没有电流流过的。因此，是否挖孔对谐振现象的产生没有影响。由于挖孔面积占总面积的比例一般不大，因此挖孔设计对谐振频率大小影响也较小。

3 结论

(1) 谐振频率大小的影响因素有输入同轴线数、外圈半径、绝缘介质相对介电常数和输入结构，其中输入同轴线数与谐振频率大小成正相关，外圈半径和绝缘介质相对介电常数与谐振频率大小成负相关，而输入结构将使谐振频率值降低。各因素的影响机制为：输入同轴线数和外圈半径的影响机制相同，均是通过改变相邻输入脉冲源间的角向距离来改变谐振频率对应的波长；绝缘介质相对介电常数则是通过改变波速来改变频率；输入结构产生的非TEM模可等效为一并联电容，减小了谐振频率。

(2) 可通过增加输入同轴线数，减小外圈半径或绝缘介质相对介电常数及合理设计输入结构，使谐振频率远离其工作频率范围。对Z-800装置而言，在原有设计基础上各参数单独变化的范围为：输入同轴线数应大于22；外圈半径应小于17.5 m；绝缘介质相对介电常数应小于115。