钢管约束型钢混凝土圆柱承载力的神经网络分析模型研究*

刘 坚 招 渝 王飞程 刘长江 曾嵘森 周观根 戚玉亮 任 达 陈 原 肖海鹏 彭林苗

(1.广州大学土木工程学院， 广州 510006； 2.广东省复杂钢结构工程技术研究中心， 广州 510006；3.浙江东南网架股份有限公司， 杭州 311200； 4.广州建筑产业研究院有限公司， 广州 510000)

钢与混凝土组合结构是以钢筋混凝土结构与钢结构为基础发展而来，具有承载能力高、刚度较大、耐火性能好等优点[1]。在原有钢管混凝土结构的基础上又发展了钢管钢筋混凝土结构与钢管型钢混凝土结构，其理念都是进一步提高对核心混凝土的约束效果[2-3]。由此理念，钢管约束型钢混凝土能有效结合钢管约束混凝土和型钢混凝土结构的优点，混凝土受钢管的约束效应，能有效提高其延性及变形能力，钢管上下两端断开，不直接承担纵向荷载，仅受环向拉应力，避免了钢管局部屈曲，可充分发挥钢材强度。与钢管约束混凝土结构相比，由于存在型钢，其刚度与承载力大幅提升；相比于型钢混凝土结构，则无需绑扎钢筋，可避免型钢混凝土施工量大和施工复杂的问题，且在相同含钢率下，钢管约束型钢混凝土具有更高的承载能力[4-6]。

影响钢管约束型钢混凝土受压承载力的参数众多，且相互耦合，呈现非线性特征；其次内部型钢对于混凝土起约束作用，且不同截面形式的型钢对混凝土约束效应也存在差异，受力机理十分复杂；使用假定主要变量的经验或解析公式，再通过试验结果进行回归模拟的传统方法，难以准确计算钢管约束型钢混凝土的承载性能。

BP人工神经网络由多个神经元组成，能模拟人脑神经系统对输入的外界信息进行处理及输出信号的过程，在BP人工神经网络模型中被简化为使用数学方法对输入数据进行运算并输出特定信号的过程。BP人工神经网络可以通过增加输入参数来考虑更多的主要影响因数，且可模拟高度非线性的系统，适用于理论模型建立有较大困难的情况。该方法在土木工程领域已有众多应用[7-11]。

目前，已有国内外学者使用BP人工神经网络对钢管混凝土构件承载力进行模拟，文献[12-13]使用BP人工神经网络对圆钢管混凝土柱进行模拟，结果显示，与解析模型相比BP神经网络模型具有更好的预测效果，Naderpour等[14]分别使用数据分组处理、基因表达式编程、BP人工神经网络三种方法对FRP约束混凝土的抗压强度进行预测，结果表明，BP人工神经网络模型的预测精度最高。张清允等[15]对矩形钢管混凝土柱承载力建立两种BP人工神经网络预测模型，并与规范计算值进行比对验证，结果表明BP人工神经网络有较好的预测精度和可靠性，Wang[16]基于神经网络对偏心荷载作用下方钢管混凝土柱进行建模，预测与试验值吻合较好。Tran等[17]开发了一种实用的人工神经网络工具来预测超高强圆钢管混凝土柱轴压性能，结果表明，人工神经网络的预测精度比传统公式计算方法有所提高。Du等[18]构建了2个人工神经网络模型(ANN1、ANN2)以预测矩形钢管混凝土柱的轴压承载力。ANN1与ANN2的输入层参数分别为5个和10个。ANN1与ANN2的预测结果表明神经网络模型具有良好的预测和泛化能力，最后用ANN1和ANN2进行了参数研究。

神经网络在组合结构承载力预测中取得了一定的进展，但发展中仍有阻碍，其中如何选取较优的隐含层节点个数及增强网络的可理解性亟待解决。

针对现有钢管约束型钢混凝土计算公式准确性不足，收集已有试验数据，建立了基于BP人工神经网络算法的神经网络分析模型，为优化网络模型采用试凑法优化隐含层节点个数，对H形和十字形型钢的圆钢管约束型钢混凝土轴心受压和偏心受压柱的峰值承载力神经网络分析模型进行了研究，同时对网络模型进行敏感性分析，研究各参数对承载力的影响程度，增强神经网络的可理解性。

1 钢管约束型钢混凝土承载力神经网络分析模型的建立

1.1 神经网络结构

BP人工神经网络采用基于多层网络的误差反向传播学习算法，由输入层、隐含层和输出层组成，见图1，计算预测结果时，各层节点之间通过权值w和阈值b进行逐层计算与传递数据，得到输出值，然后计算输出值与目标值的误差，通过反向传播计算每一层误差的影响梯度，从而更新权值和阈值，重复正向与反向过程，实现减小计算值与目标值误差，以此达到训练神经网络分析模型的目的。

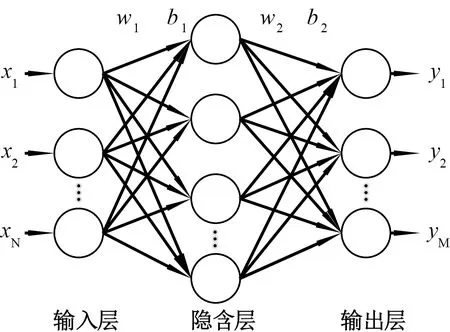
图1 三层BP人工神经网络Fig.1 Three-layer artificial neural network

1.2 10参数神经网络分析模型

输入层参数选取采用Mander公式计算约束混凝土的抗压强度，并结合试验提出了钢管约束混凝土短柱的轴压承载力公式。同时考虑偏心荷载的影响，选取钢管高度、钢管直径、钢管厚度、钢管屈服强度、型钢含钢率、型钢截面形式、型钢屈服强度、混凝土轴心抗压强度、截面偏心距和开槽方式，10个参数作为BP人工神经网络的输入值，以TSRC圆柱受压承载力作为输出值，各参数的数值范围通过整理现有试验研究[19-22]中收集的54组试验数据(其中TSRC柱轴压试验为39组，偏压试验为15组，分别依据峰值承载力从小到大进行编号)进行确定，各参数数值、钢管的开槽方式和型钢截面见表1和图2，开槽方式见图2a、b、c，其中图2a在钢管两端分别切开1个环形条带，使钢管与两端分离，不直接承受纵向荷载，避免局部屈曲，图2b在钢管两端及钢管中间共切开3个环形条带，图2c在钢管两端处及钢管中部共切开5个环形条带，随着开槽数越多，钢管与混凝土之间的摩擦力及黏结力越小，纵向应力也随之减小，环向应力能更充分发挥，对混凝土的约束能力越强。型钢截面如图2d、e所示分为H型钢和十字型钢。

a—m=1； b—m=2； c—m=3； d—n=1； e—n=2。图2 TSRC柱开槽方式和型钢截面形式Fig.2 Slotting methods and steel section shapes for TSRC columns

表1 输入参数数值Table 1 Input parameter values

1.3 神经网络分析模型样本选择与分类

收集TSRC圆柱轴压和偏压的试验数据，需要剔除偶然数据的影响，即排除影响参数接近，但峰值承载力却大幅偏离的少数试件样本。依据人工神经网络的内插性特点，选择具有代表性的试验作为样本。其中代表性是指影响参数的数值范围尽可能大，代表的情况越多，包含的信息范围越广，BP网络训练精度也就越高。将整理出的54组试验数据[19-22]分为训练集、验证集和测试集三部分，各样本集分别占比为0.7∶0.15∶0.15，即38∶8∶8，其中训练集分别选取不同径厚比、不同强度等级钢材、不同截面形式、不同偏心距和不同长细比等不同特征的试验构件，以保证神经网络分析模型对各种情况的适用能力，测试集和验证集从测试集外的样本中随机选取。通过训练集训练BP人工神经网络，验证集确定误差较低的权值和阈值，再使用测试集评估选出模型的好坏，确保模型具有较好的泛化能力。

1.4 训练参数设置及隐含层个数选取

为加快收敛速度和避免数值问题，对数据进行归一化处理，大小在0.1～0.9范围内，采用对数sigmoid函数作为传递函数，学习率lr为0.001，控制误差为0.000 1，最大训练步数为1 000，学习算法采用LM算法，适用于中等网络，占用内存大，学习速度快，其权值修正根据式(1)计算：

dX=-([jX]T[jX]+[I]*mu)-1[jX]T{E}

(1)

式中：jX为误差对权值微分的Jacobian矩阵；I为单位矩阵；mu用于确定是根据牛顿法还是梯度法进行计算的调整值；E为误差向量。

为避免symmetry breaking(对称失效)问题，初始权值采用随机数初始化，不同的初始权值可能收敛于局部最优而非全局最优，为选取合适的隐含层节点个数，采用试凑法，使用式(2)对隐含层节点数进行初步估算[23]。

(2)

式中：p为隐含层节点数；n为输入层节点数；q为输出层节点数；a为系数，取 [1,10]。

以上述公式作为参考，适当扩大试凑范围，将隐含层节点数取为5～20，分别对不同隐含层节点数进行1 000次训练，此时各结果较稳定，取1 000次训练中总训练数据的均方误差MSE最小的模型作为比较对象，分别比对不同隐含层节点数的MSE及相关系数R，相关系数R与隐含层节点数的关系见图3，均方误差MSE与隐含层节点个数的关系见图4，根据图3和图4，隐含层节点数为12的BP人工神经网络模型的训练集、验证集和测试集具有较高的相关系数，各样本集相关系数的大小相差较小，比较稳定，且均方误差MSE最小，该BP人工神经网络模型具有最好的性能。因此取10个节点数作为BP人工神经网络模型输入层，隐含层节点数为12，输出层节点数为1，用N10-12-1表示该模型。

图3 各隐含层节点数对应的相关系数RFig.3 Correlation coefficient R corresponding to the number of nodes in each hidden layer

图4 各隐含层节点数对应的均方误差(MSE)Fig.4 Mean square error (MSE) corresponding to the number of nodes in each hidden layer

2 目前钢管约束型钢混凝土承载力公式计算结果及对比分析

TSRC圆柱轴压构件依据JGJ/T 471—2019《钢管约束混凝土结构技术标准》的承载力计算式，见式(3)。

Nu=fccAc+Aafa

(3a)

(3b)

式中：fa为型钢屈服强度；fcc为约束混凝土抗压强度；fco为混凝土轴心抗压强度；fr为恒侧压；fy为钢管屈服强度；Ac为混凝土截面面积；Aa为型钢的截面面积。

文献[22]在型钢混凝土偏压构件承载力公式的基础上，给出了圆钢管约束型钢混凝土构件偏压承载力公式，见式(4)：

N=fccbx+faAa-σsAa

(4a)

Ne=fccbx(h0-x/2)+faAa(h0-a)

(4b)

(4c)

式中：f′c为混凝土圆柱体抗压强度；θ为套箍指标；ρ为配钢指标；e为型钢受拉翼缘合力点与轴向力作用点间的距离；a为型钢受拉翼缘至截面受拉边缘的距离；h0为受拉型钢翼缘至截面受压边缘的距离；x为受压区高度。

采用TSRC圆柱轴压式(3)对54组样本中39组轴压样本进行计算研究，使用偏压式(4)对15组偏压样本进行分析，计算结果见图5、6。54组样本的最大误差为36.2%，平均误差为10.4%。

a—中长柱； b—短柱。图5 式(3)计算值与试验值轴压承载力对比Fig.5 Comparisons of axial bearing capacity between formula (3) calculated values and experimental values

a—中长柱； b—短柱。图6 式(4)计算值与试验值偏压承载力对比Fig.6 Comparison of eccentric-loaded capacity between formula (4) calculated values and experimental values

图5a、6a显示，对于中长TSRC圆柱，由公式计算的轴压和偏压的峰值承载力结果普遍高于试验值。由图5b、6b可见，就轴压和偏压TSRC圆短柱的峰值承载力而言，公式的计算结果大部分低于试验，偏向保守。

3 神经网络分析模型承载力计算结果及对比分析

采用N10-12-1神经网络分析模型(简称：N10-12-1模型)对54组TSRC圆柱样本峰值承载力进行计算研究，将N-10-12-1模型计算值、现有公式计算值与试验值进行对比(图7、8)。N10-12-1模型总样本最大误差6.08%，平均误差为1.78%，训练集最大误差6.08%，平均误差1.52%，验证集最大误差5.80%，平均误差1.85%，测试集最大误差5.25%，平均误差2.94%。

图7 各种计算值与试验值轴压承载力对比Fig.7 Comparison of axial compression capacity between calculated and tested values

图8 各种计算值与试验值偏压承载力对比Fig.8 Comparisons of eccentric-loaded capacity between calculated values and tested values

N10-12-1模型的预测结果总体看误差较小，可以较充分考虑中长柱加载过程中因发生的侧向挠度和弯曲，所产生的稳定性问题。且内部型钢对于核心混凝土的约束效应、构件的高度、钢材进入塑性强化阶段、不同的荷载情况对于TSRC柱承载力的影响，从预测结果上看，也都考虑到了，可见模型在参数最大数值范围内能较好地预测钢管约束型钢混凝土的极限承载力，具有良好的计算能力。

由公式计算的TSRC短柱轴压和偏压承载力均普遍低于试验值，在工程应用中偏于安全；而TSRC中长柱的轴压和偏压承载力公式计算结果数值均高于试验值，主要是由于没能在公式中反映中长柱稳定问题对受压承载力的影响。

综上，N10-12-1模型不论对于TSRC短柱还是TRSC中长柱的轴压、偏压承载力预测都能获得良好的精度，能较为充分地考虑各主要参数的影响，具有较强的适应性，是一种较好的计算方法。

尚需指出，BP神经网络具有泛化能力，但该能力一般仅在输入参数在最大数值范围内有效，对于超出参数最大数值范围的输入，会随着超出范围的增大，产生越大的计算误差[24]，即一般BP神经网络具有内插值特性，而不具备外推能力。目前，随着TSRC结构试验进一步开展，可不断添加新的试验样本，提高学习样本数据的完备性，促进神经网络分析模型不断学习完善，进一步扩展神经网络分析模型计算承载力的应用范围并提高计算精度。

神经网络分析模型不具备可视化公式或操作,为增强神经网络分析模型的可复制性，表2给出了训练后神经网络的连接权值矩阵，其中iw、b1为输入层到隐含层的连接权值和阈值，lw、b2为隐含层到输出层的连接权值和阈值，其中b2=-0.734 1。

表2 神经网络连接权值和阈值Table 2 Neural network connection weights and bias

4 神经网络分析模型敏感性分析

敏感性分析可用于研究和预测假设模型的输入值对输出值的影响程度，衡量影响程度大小的值称为敏感性系数，其值越大，对神经网络分析模型的输出值的影响程度越大，通过分析敏感性系数，可研究BP人工神经网络各输入参数对钢管约束型钢混凝土峰值承载力的重要性，增强BP人工神经网络的可理解性[25-27]。采用基于BP人工神经网络连接权的敏感性分析Garson算法，通过使用连接权值的乘积来计算输入值对输出值的影响程度。因为连接权值有正有负，原本的公式会弱化输入值xi对yk的影响，因此采用改进后的Garson算法，输入值对输出值的敏感性系数计算见式(5)。

(5)

式中：N为输入层节点个数；L为隐含层节点个数；wij为输入层i节点与隐含层j节点连接权值；vjk为隐含层j节点与输出层k节点连接权值。

通过对神经网络分析模型进行敏感性分析，可以得到如图9所示的各输入特征对TSRC圆柱峰值承载力的影响程度和重要性，分析结果表明，截面偏心距对TSRC圆柱峰值承载力神经网络分析模型影响最大，钢管直径、型钢含钢率和型钢的截面形式次之，均对计算结果有较大影响，而高度对采用神经网络分析模型计算TSRC圆柱峰值承载力的影响最小。由此可知各影响参数对TSRC圆柱承载力的贡献大小。参考相关文献试验研究[22]，径厚比和偏心率变化对构件承载力影响较显著，对应敏感性分析系数中的直径、钢管厚度、偏心距三个参数，其中直径的变化还将影响构件的截面面积，因此敏感性系数较大，参考钢管混凝土，长细比对承载力影响较大，其中由于现有试验数据中长细比范围在3～6之间，取值范围较小，导致影响程度较小，因此高度的敏感性系数偏小。综合上述分析，敏感性分析对TSRC圆柱构件设计具有一定的参考意义。

图9 N10-12-1模型敏感性分析结果Fig.9 Sensitivity analysis results of N10-12-1 model

5 结束语

在已有的TSRC圆柱试验数据和承载力计算式的基础上，提出10参数TSRC圆柱承载力神经网络分析模型，并将神经网络分析模型的计算结果与现有公式的计算结果进行对比，主要结论如下：

1)采用神经网络分析模型对钢管约束型钢混凝土的轴心受压及偏心受压的承载能力进行研究，通过均方误差MSE及相关系数R确定了最优的隐含层节点个数，提出10参数N10-12-1神经网络分析模型。

2)通过对比分析，神经网络分析模型的计算结果与试验结果吻合较好，能合理地计算钢管约束型钢混凝土的承载力性能。可见神经网络分析模型模拟钢管约束型钢混凝土受力中各变量复杂非线性关系的可行性。但要想实现更为广泛的应用，还需扩大输入参数的覆盖范围，增加更多具有代表性的训练样本，以此进一步优化该神经网络分析模型。

3)通过改进的Garson算法对10个参数进行敏感性分析，定量描述10个参数对输出值的重要性程度，得到各参数对神经网络分析模型的影响规律，发掘出各参数间的非线性关系，可作为改进神经网络分析模型的参考条件，并在一定程度上供实际设计参考。