考虑SSI 效应的核电厂直立翼墙与排水沉管交叉体系静动力响应分析1
尹训强 付忠余
(大连大学, 建筑工程学院, 大连 116622)
引言
核能是优化能源结构的重要清洁能源,已然成为实现碳中和、碳达峰的重要选项。在核电的不断更新换代中,工程构筑物的抗震能力依旧是保障核电安全的首要问题(孔宪京等,2013;Onitsuka 等,2019)。
压水堆核电机组的联合泵房及两侧翼墙要保证循环冷却水系统供水,属于抗震I 类物项,尤其是非常规的交叉设计,考虑土-结构动力相互作用(简称SSI)效应的影响是开展其抗震安全性评价的关键内容。目前,国内外学者针对考虑SSI 效应的核电厂抗震分析开展了广泛的研究。Wang 等(2017)采用透射边界分析了SSI 效应对核电厂工程结构在垂直入射地震激发下响应的影响。陈少林等(2020)提出一种模态叠加和时步积分结合的土-结相互作用分区算法,开展了CAP1400 核电结构的地震响应分析。尹训强等(2020)提出基于施加高阻尼并逐步移频抽取思想的阻尼溶剂逐步抽取法考虑SSI 效应,并分析了某核岛厂房的地震响应规律。金煜皓等(2015)通过在地基有限域外边界施加粘性边界的方式考虑无限地基辐射阻尼的影响,开展了对核岛厂房结构地震响应影响的研究。赵密等(2020)基于黏弹性人工边界和斜入射地震动输入方法研究了非基岩场地中核岛结构地震响应规律。上述研究中的研究对象基本为单一核电厂工程结构,针对核电厂抗震I 类物项且为交叉设计工程结构的地震响应分析较少。
本文以国内某核电厂的联合泵房两侧直立翼墙-排水沉管交叉体系为研究对象,精细化模拟地基材料的力学特性及交叉体系的空间分布形态,考虑静动力荷载联合作用、无限地基辐射阻尼以及地基非均质特性等影响,基于ANSYS 平台建立翼墙-沉管交叉体系-地基动力相互作用分析模型,进而探究交叉体系结构的应力、变形及加速度峰值等响应的变化规律。
1 工程概况
取水工程构筑物包括联合泵房、直立翼墙、取水导流堤以及内护岸。联合泵房西侧直立翼墙长35 m,东侧直立翼墙长25 m,采用现浇沉箱结构,与两侧内护岸连接,翼墙顶高程为9.1 m。
依据提供的设计方案,翼墙结构共由9 个沉箱构成(图1),沉箱平面布置与排水沉管相对位置如图1 所示,1~6 号翼墙结构尺寸为30.75 m×7.45 m×17.9 m(长×宽×高),4~9 号翼墙尺寸为37.45 m×7.45 m×17.9 m (长×宽×高),并且7~9 号直立翼墙直接坐落于排水沉管之上,该部分翼墙承重于沉管并与排水沉管垂直交叉接触,各个沉箱之间预留50 mm伸缩缝,沉箱内部依次填充堤心石、碎石、二片石垫层至密实;排水沉管采用一机一洞,双孔共壁的结构形式,排水沉管长670 m,单孔尺度为5.3 m×5.3 m,外壁厚1.5 m,内壁厚0.5 m,其上部承受厂区回填土、海水重力以及翼墙结构重力作用。翼墙底部与沉管结构皆承重于微风化花岗岩地基。
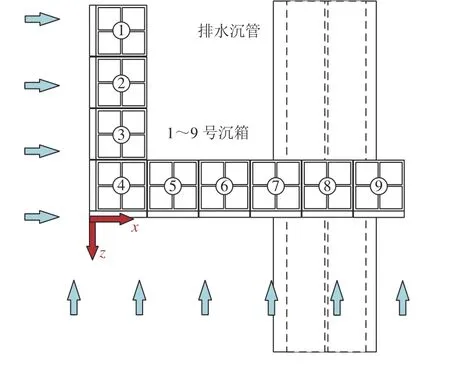
图1 翼墙-沉管交叉体系平面布置图Fig. 1 Plan layout of wing wall-immersed tube crossover system
2 静动力分析模型
翼墙-沉管交叉体系-地基静动力分析模型由直立翼墙、排水沉管、近场地基以及半无限地基构成,如图2 所示。强地震作用下,土-结构相互作用、静动耦合荷载作用以及动水压力等是需要考虑的关键技术问题。
2.1 SSI 效应的模拟
粘弹性人工边界模型具有空间解耦特性、便于与通用有限元程序整合的特点,且计算效率高,易于掌握,近年来在核电工程结构的抗震安全分析中得到广泛发展和应用。本文通过在截断边界处设置粘弹性人工边界考虑SSI 效应,如图2 所示,核心思想是借助弹簧阻尼器的作用耗散反射波波动能量,而弹簧单元可提供竖向约束及弹性恢复力,并通过施加等效节点荷载力的形式实现地震动的输入,三维分析中等效节点力的计算公式为:

图2 翼墙-沉管交叉体系-地基静动力分析模型Fig. 2 Wing wall-immersed tube crossover system-soil static and dynamic analysis model


2.2 静动力分析方法
翼墙-沉管交叉体系会受到水压力、土压力等静力荷载及地震动荷载的联合作用,传统的静动荷载通常将静力与动力荷载分开考虑后进行工程叠加,这种做法很难保证静、动模型的统一。本文采用尹训强等(2016)提出的基于极大初始时间步法的静动力耦合分析算法,可保证结构在静动荷载耦合激励下获得合理的地震响应。该方法基于Newmark 积分算法的隐式求解特点,对初始动力分析时间步进行极大化处理,弱化时间效应的影响,其计算表达式与静力分析类似,仅在边界刚度有一定差别,如式(3)所示。

式中,Kb为Kn与Kt所组成的边界刚度矩阵,下标“ss”和“bb”分别为广义结构内部节点和边界节点,下标“sb”和“bs”为内部节点和边界节点耦合项;Fa为所施加静荷载。
2.3 基于UPFs 的用户单元
基于ANSYS 软件二次开发能力,通过修改FORTRAN 接口子程序,采用User Programmable Features(简称UPFs)编程方式实现用户单元功能的嵌入。为模拟SSI 效应,通过子程序UserElem.F 编译创建粘性人工边界单元,具体流程及验证参考李浩然等(2017)文献。
另外,按照Westergaard(1933)公式计算顺流向地震动水压力,并采用施加附加质量单元的方式模拟,本文所用具体表达式如下:

式中,ah表示地震动加速度幅值;ρw表示海水密度;h表示海平面至直立翼墙底部的总高度;y表示某节点处的水深。
2.4 计算模型的建立
通过ANSYS 中嵌入的粘弹性人工边界单元模拟SSI 效应,建立翼墙沉管结构-地基土体系统三维有限元模型(图3),地基模拟范围从结构两侧向外各延伸40 m,从底板向下延伸40 m,沿东侧翼墙轴向方向各延伸40 m。翼墙与沉管交叉结构有限元模型如图4 所示,采用SOLID185 实体单元模拟,大部分为六面体单元,少部分五面体用于适应局部复杂的结构形状或作过渡用;考虑地基土剪切波速与地震最高振动频率等影响,取结构部分单元尺寸不超过1.5 m,地基部分单元尺寸不超过4 m。

图3 交叉体系-土相互作用分析模型Fig. 3 Analytical model for crossover system-soil interactions

图4 翼墙与沉管结构有限元模型Fig. 4 Finite element model of wing wall and immersed tube structure
本次计算分析所用材料参数如表1 所示。地基岩体主要为微风化花岗岩,并有部分中风化花岗岩层,基础之上翼墙支护部分厂区回填土为凌体石块与厂区回填料,边坡采用1~300 kg 开山石放坡。交叉体系结构及地基的材料阻尼采用 Rayleigh 阻尼,振型阻尼比为 0.05。静动力参数的修改可通过ANSYS 中的重叠单元和生死单元实现。
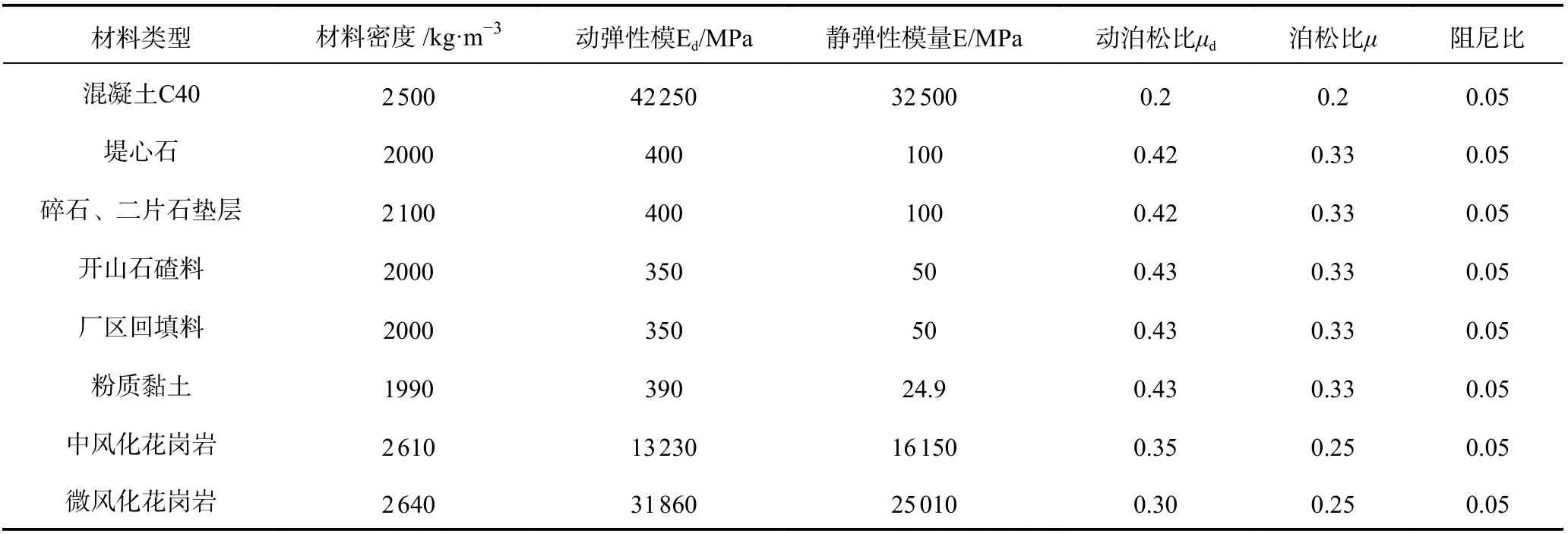
表1 三维抗震模型分析材料计算参数Table 1 The material calculation parameters of 3D seismic model analyzes
3 交叉体系-地基系统静动力耦合分析
采用本文建立的翼墙-沉管交叉体系-地基静动力分析模型,开展多荷载联合作用下交叉体系静动力响应分析。
3.1 荷载作用
依据《核电厂抗震设计标准》(GB 50267−2019)(中华人民共和国住房和城乡建设部,2019)规定,抗震计算中主要考虑正常运行作用与严重环境作用或极端环境作用的作用效应组合,本文采用SL-2 地震动对交叉体系进行校核。主要考虑的荷载效应包括结构自重、静水压力(设计高水位为2.26 m)、固定设备荷载、侧向土压力及地震作用。SL-2 级基岩水平峰值加速度设计值取0.15g,竖向峰值加速度取0.10g,时间步长为0.01 s,持时25 s,相应的地震动时程如图5 所示。

图5 输入地震动时程曲线Fig. 5 Time history curve of the seismic wave
3.2 计算结果分析
3.2.1 应力分析
图6 给出翼墙与沉管交叉体系的第一主应力与第三主应力分布云图。由图可知, 第一主应力与第三主应力在翼墙与沉管接触部位的变化均较为明显,且7~9 号翼墙与沉管的交叉部位出现较强的应力集中现象。第一主应力最大值为4.44 MPa,位于交叉部位前部,第三主应力最大值为−10.70 MPa,位于交叉部位后方两侧位置。由此可知,在强震作用下,翼墙结构受后侧土体侧向压力作用,在翼墙后方产生拉应力区域,同时翼墙结构为抵抗后侧土体的侧向压力,而在底部边界部位产生反弯矩,从而在交叉部位前部产生较大应力,导致接触位置边缘区域出现应力集中现象。
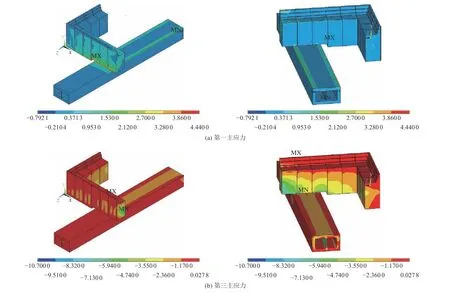
图6 交叉体系结构应力云图(单位:兆帕)Fig. 6 The principal stress of crossover system(Unit: MPa)
3.2.2 加速度响应分析
为研究翼墙与沉管结构的加速度响应变化规律,选取4~9 号翼墙结构不同高程及沉管结构沿线处的监测点,其分布如图7 所示。

图7 交叉体系加速度监测点分布Fig. 7 Crossover system acceleration monitoring point distribution
提取不同翼墙结构在不同高程处的节点加速度峰值变化,如图8 所示。从图中看出,翼墙加速度峰值随高度增大而增大,在同一高程下,位于沉管上部的8 号翼墙与沉管接触部位水平方向的加速度峰值较小,分别为0.803 m/s²与0.927 m/s²,而在竖直方向8 号翼墙底部加速度峰值最大,为0.823 m/s²。由此可知,排水沉管对翼墙接触部位水平向加速度影响较小,而对竖向加速度影响较大。
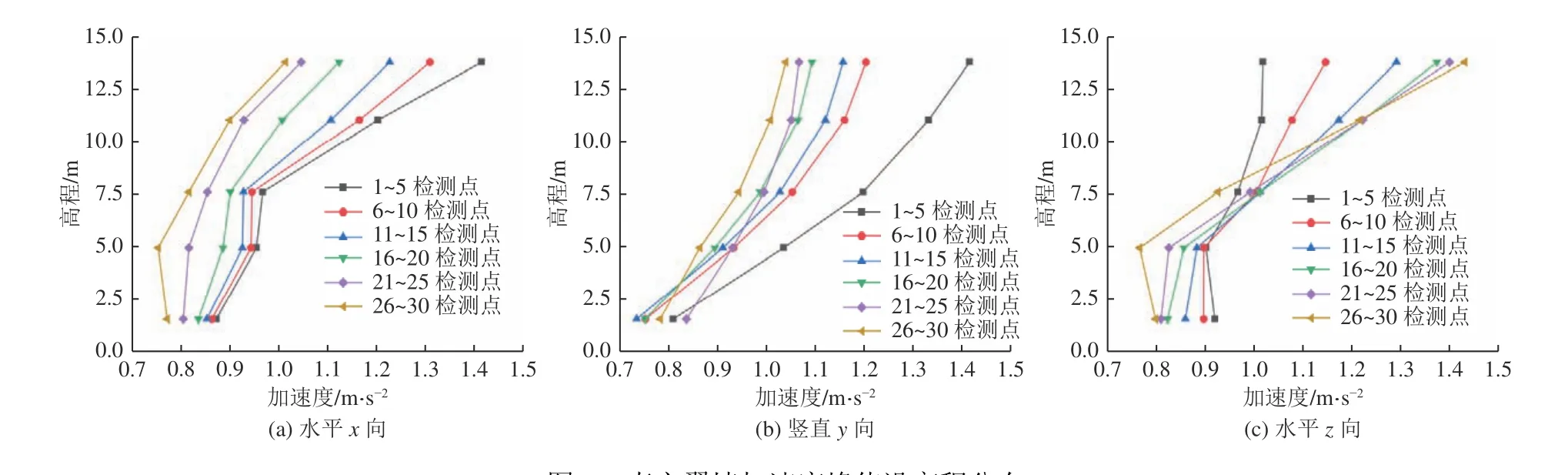
图8 直立翼墙加速度峰值沿高程分布Fig. 8 Peak acceleration distribution along the elevation of the upright wing wall
提取沉管不同水平位置处的节点加速度峰值变化,如图9 所示。从图中看出,沉管结构三向加速度峰值在交叉部位有显著增加,其中x向加速度最大值出现在交叉部位,为0.881 m/s²;y轴竖向加速度峰值在交叉部位增大,最大值为0.821 m/s²;z向加速度最大值位于交叉部位后方,为0.980 m/s²。由此可知,水平方向上加速度峰值受到翼墙相互作用而增大,且在接触范围内增加幅度较大,而对于竖直方向,由于沉管上部翼墙质量远大于沉管上部回填土,在翼墙部分迎水面正下部的沉管部分,加速度峰值明显增大。
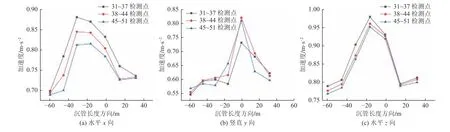
图9 排水沉管加速度峰值顺管线分布Fig. 9 Peak acceleration distribution along the tube line of drainage immersed tube
3.2.3 位移响应分析
交叉体系位移变形分布如图10 所示。由图可知,交叉体系最大位移变形发生在翼墙结构顶部,分布范围为[−7.74 mm, −2.08 mm],x方向最大位移变形出现在2、3 号翼墙顶部以及9 号翼墙上部,为7.50 mm;y方向最大位移变形出现在7~9 号翼墙后方顶部边缘,为3.68 mm;z方向最大位移变形出现在8 号翼墙前顶部边缘,为7.74 mm。另外,在同一高程下,位于沉管上部的翼墙位移变化更为明显,由此可知,与岩性地基相比,排水沉管在强震作用下对直立翼墙位移变形影响更大。

图10 交叉体系位移变形分布云图(单位:毫米)Fig. 10 Cloud map of displacement deformation distribution of crossover system(Unit: mm)
4 结语
本文聚焦直立翼墙与排水沉管交叉体系,基于UPFs 创建了粘弹性人工边界单元考虑SSI 效应,建立了翼墙-沉管交叉体系-地基静动力分析模型,并开展了交叉体系在多荷载耦合效应下的静动力响应分析,主要结论如下:
(1)翼墙与沉管交叉体系的主应力在两结构接触处的变化明显,且主拉应力的最大值出现在翼墙挡水侧底部与沉管的交界处,有较强的应力集中现象。
(2)沉管上方8 号翼墙结构水平向加速度峰值受沉管影响较小,与其他变化规律基本一致,而竖向加速度峰值在底部有较大变化;沉管结构的三向加速度峰值在交叉位置处有显著增加。
(3)沉管上方8 号翼墙结构的位移变形有较大变化,且竖直y向与水平z向的最大值出现在此翼墙顶部区域;沉管在交叉部位的响应同样也有较显著的增大。

