面向微观仿真参数敏感区间的参数选取——以交织区为例

聂欣月， 单籽跃， 周晨静*， 刘莲莲

(1.北京建筑大学土木与交通工程学院， 北京 100044； 2. 北京交科公路勘察设计研究院有限公司， 北京 100191)

微观交通仿真技术可描述复杂多变的交通流现象，在工程实践与科学研究中得到了广泛的应用，其中微观仿真模型参数标定是微观交通仿真技术应用的前提。在以往研究与实践中，国内外学者对微观交通仿真模型参数标定流程有了统一的认识，且应用智能优化算法[1-2]开展参数寻优成为常见手段。对于参数寻优标定工作，张月[1]开发了一个高效准确的参数校正程序，在此基础上，研究者通过研究参数集选取及确定[3]、校核指标选定[4-5]、参数取值[6]等步骤优化参数标定流程；或基于现有寻优算法自身缺陷，引入其他方法改进算法[2，7]，以期得到更加高效、准确的仿真标定方法。梳理文献发现若仅关注改进智能算法，而不探讨选取的参数集类型及其取值范围的合理性，标定的仿真模型输出结果可移植性差。

2004年Cohen[8]发现个别参数对仿真结果产生较大影响，提出关键参数的概念，成为研究仿真参数敏感性的开端。参数的敏感性研究是指通过分析模型参数对宏观交通流特性参数的敏感性，定量描述模型输入参数变量对输出变量重要性程度来达到求算的目的。随着对仿真标定流程的深入研究，越来越多的学者[9-10]发现微观仿真参数的敏感性研究对参数标定工作的重要性。通过参数的敏感性研究可以排除对校核指标灵敏度低的参数，从而减少标定参数数量，有效降低参数标定工作量。因此，研究者聚焦于参数敏感性的校核指标选取[3,9-10]以及如何高效求解敏感性参数方法[2,11-14]。

刘洪启[9]研究了基本路段和交织段等不同道路设施对速度敏感性的评估，并采用速度变化百分比反映敏感程度，用以指导城市道路模型的校正。周晨静等[3]通过比对不同宏观参数的敏感参数个数，得出选用车均延误作为校核指标最为合适。 Chaudhari等[10]提出根据轨迹数据校准模型参数标定，基于微观性能指标加速度、速度和轨迹曲线估计校准参数，与已有混合交通校准方法更为准确。众多学者在敏感性分析方法的技术使用上也进行了多样化且先进的探索。朱林波等[11]基于反向传播(back propagation，BP)神经网络对模型参数进行灵敏度分析，利用改进的Garson公式计算各输入变量对评价指标的相对敏感度系数，校准具有较高灵敏度系数的参数，从而降低参数校准的复杂性。Siddarth等[12]使用拉丁超立方采样技术用于减少需要测试的样本数量，利用方差分析与初级效果(elementary effects，EE)进行敏感度分析，最终确定灵敏参数。Jehad等[13]利用EE方法以均值、标准差、绝对均值作为敏感性指标，对VISSIM仿真参数进行敏感性分析，得出影响驾驶行为最为显著的6个参数，应用于高速公路异构交通的研究。张建旭等[14]规定模型参数选取区间划分和交叉组合的规则，应用改进LH-OAT(improved Latin-Hypercube-one factor at a time，ILH-OAT)算法实现参数的灵敏度分析，保证高精度条件下，达到有效简化模型的目的。 Liu等[2]基于机器学习(machine learning，ML)和粒子群优化(particle swarm optimization，PSO)的方法校准微观仿真模型参数，对比4种机器学习模型，最终采取具有最好预测精度的人工神经网络嵌入PSO中，从而提高计算效率。

然而在以往研究中，微观仿真模型参数集及取值范围的选取并没有统一的准则，梳理现有文献选用的敏感性参数集以及参数范围发现其选取不尽相同，且取值空间相差很大。既有研究对参数敏感性分析给出了一定的方法性借鉴，但是不同参数具有不同的敏感特性，例如有些参数在全部取值空间均对结果具有敏感性影响，而其他参数在一定的取值空间才对结果具有敏感性影响，若超出该空间范围表现出较弱敏感性甚至成为非敏感参数。因此在参数范围选取没有科学合理的依据的情况下仅进行敏感性分析是不合理的。现通过微观仿真实验得出仿真结果随参数变化情况，以仿真结果特性为分析依据，充分考虑参数取值空间不同对仿真影响程度不同的情况，构建敏感性分析方法，确定参数的敏感区间，为参数敏感性分析提供方法和理论依据。

1 实验设计

1.1 参数取值空间求取方法设计

为求取微观仿真模型参数取值空间，研究以微观仿真实验为基础设计如下方法步骤。

步骤1确定较大范围的参数仿真取值区间。在该区间内寻找参数变化对校核指标的敏感区段。

步骤2以步骤1中确定的区间为范围，逐步变化仿真参数取值，开展微观仿真实验，获取参数变化与输出指标的量化关系。

步骤3以输出指标的变化特性为聚类标准，对数据进行聚类分析，并设计判定指标，明确敏感性分布。

1.2 实现过程

研究以快速路交织区作为仿真场景，以微观仿真软件VISSIM为平台，选取车均延误[3]作为评价指标开展仿真实验。仿真场景交织区具体构成为：A型交织区、交织长度100 m、车道数为5、交织车道数为2、匝道为单车道，车道宽度均为3.5 m。主线入口断面流量为4 000 辆/h，匝道入口断面流量为500 辆/h，车辆构成为100%小客车，交织流量比为24.4%。仿真输出评价指标选取主线车均延误，每隔300 s进行评价一次，评价时间为300～3 600 s，结果取其均值，仿真场景如图1所示。

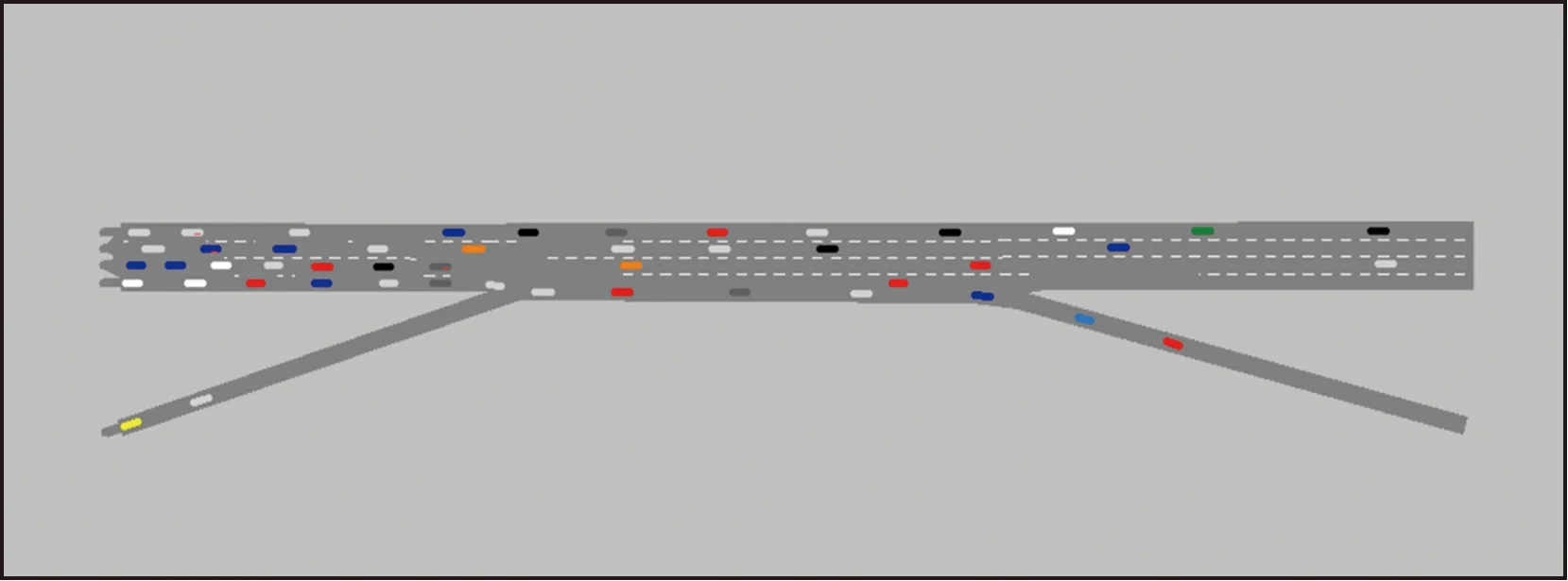
图1 仿真场景图Fig.1 Simulation scene

为分析单个参数变化对仿真结果的影响情况。采取单一变量分析法，每次只变化1个参数的取值。微观交通仿真实验仿真结果的变化由随机种子、仿真参数变化两部分因素导致。随机种子不同，仿真结果也会有差异。因此为消除随机种子造成的随机误差，每个参数选取10、30、50、70、90共5个随机种子进行实验，取其均值作为最终仿真结果。

1.3 实验参数及参数范围

为明确参数大致取值空间，对国内该领域文献中所采用的参数取值范围进行梳理，将张月[1]、周晨静等[3]、李美影[7]、胡婷[15]、章玉等[16]、金成英[17]对仿真参数取值范围进行并集计算，作为参数取值的研究空间。文献中未涉及的参数，以VISSIM仿真软件中默认值的0.5倍为研究范围左边界，默认值的1.5倍为研究范围右边界。

对适用于城市快速路和高速公路的Wiedemann99模型参数进行分析，其参数主要包括停车间距(CC0)、车头时距(CC1)、跟车变量(CC2)、进入跟车状态的阈值(CC3)、消极跟车状态的阈值(CC4)、积极跟车状态的阈值(CC5)、车速震动(CC6)、加速度波动幅度(CC7)、停车时的加速度(CC8)、80 km/h 车速时的加速度(CC9)、最大前视距离(Pobd)、最大后视距离(Robd)、可观察到的车辆数(n)，跟驰模型参数实验范围及步长如表1所示。

表1 跟驰模型参数Table 1 Car following model parameters

车道变换模型采用的是Rule-based算法，改变换道车辆和受影响车辆的减速能力，其参数主要包括：最大加速度(ACCmax)、-1 m/s2(D)、可接受加速度(ACCac)、消失前的等待时间(Tdis)、最小车头空距(GAPmin)、安全折减系数(ABX)、协调刹车的最大减速度(ACCX)，换道模型参数实验范围及步长如表2所示。

表2 换道模型参数Table 2 Lane change model parameters

2 仿真结果分析

2.1 结果特性基本分析

研究分别对20个驾驶行为参数进行实验，共开展8 270次仿真实验。对各参数仿真结果变化情况进行分析，选取代表性参数CC1、ABX、CC9、CC5变化趋势图进行阐述。参数趋势变化图如图2～图5所示。

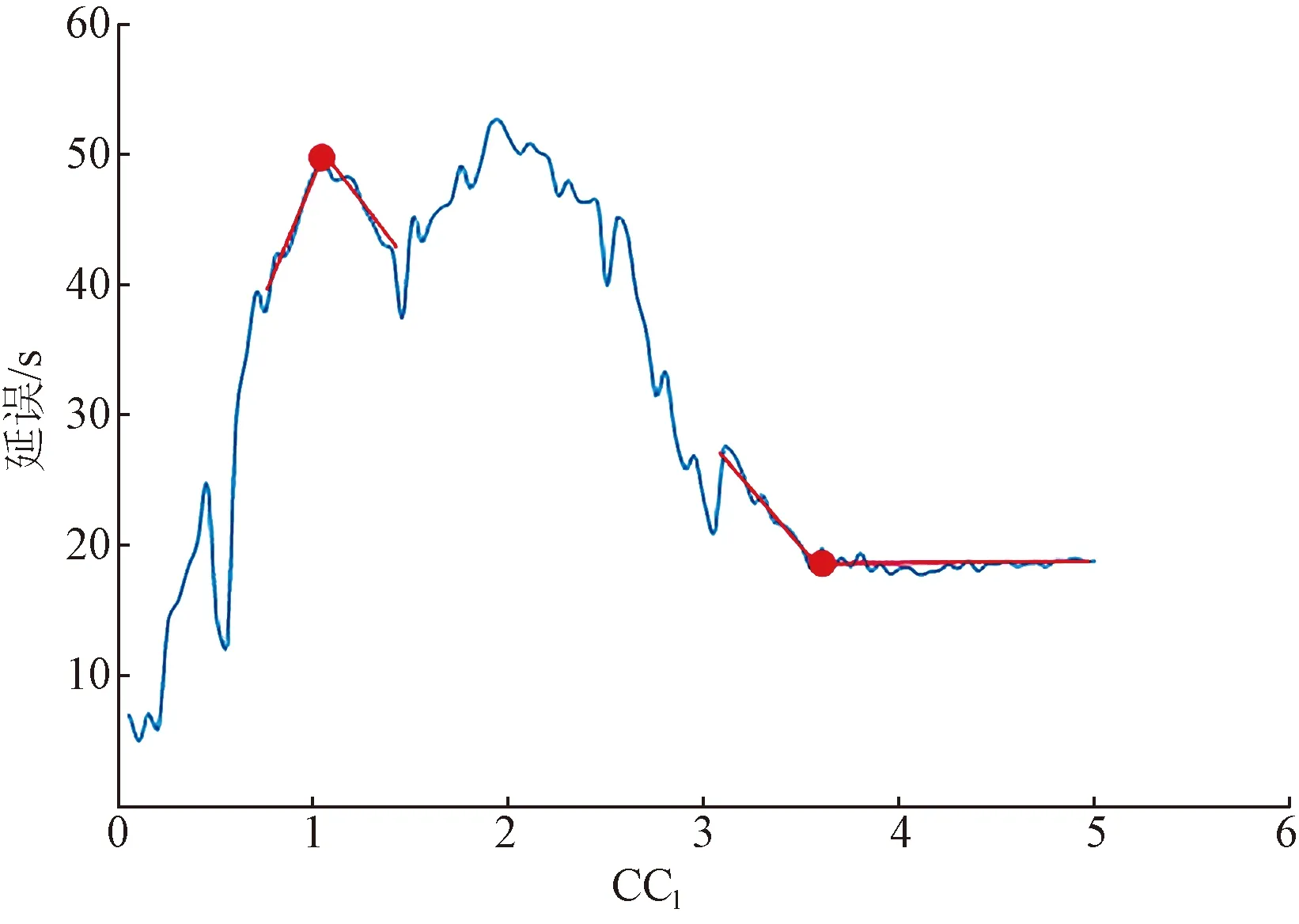
图2 参数CC1仿真结果Fig.2 Simulation results of parameter CC1

图3 参数ABX仿真结果Fig.3 Simulation results of parameter ABX

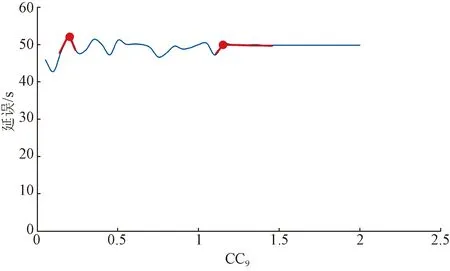
图4 参数CC9仿真结果Fig.4 Simulation results of parameter CC9

图5 参数CC5仿真结果Fig.5 Simulation results of parameter CC5

从参数变化趋势上看，不同参数的仿真结果变化趋势有所不同。参数CC1整体上呈现先上升后下降最后趋于平缓的趋势，参数ABX仿真结果的变化趋势由缓慢上升转换为急速上升的趋势，参数CC9仿真结果和其他参数相比，整体上趋于平缓，参数CC5的仿真结果在整个研究空间上变化具有相似性。虽然各个参数的仿真结果整体变化趋势不同，但变化趋势呈现为一定的阶段性，仿真结果变化趋势在参数某一局部取值空间内具有相似性。以ABX为例，仿真结果在参数取值空间(0, 0.40)和(0.40, 0.50)上，具有不同的变化趋势。在取值空间(0, 0.40)上，仿真结果变化趋势基本相似，均呈现缓慢增长趋势，而在取值空间(0.40, 0.50)上仿真结果为急剧增长趋势。同时仿真结果变化波动的剧烈程度不同，以参数CC9为例，在取值空间(0,1.20)上仿真结果具有波动性，而在取值空间(1.20, 2.00)上，仿真结果几乎无波动。

由此可得，随着参数取值的变化，仿真结果的变化趋势不同，趋势变化可总结归纳为以下6种：由上升趋势转为下降趋势，由下降趋势转为上升趋势，由比较缓慢变化趋势转为较剧烈的上升或下降趋势，由较剧烈的上升或下降趋势转为较缓慢的变化趋势。趋势变化示例如图6(a)～图6(f)所示，趋势变化点可分为极值点和拐点两类。

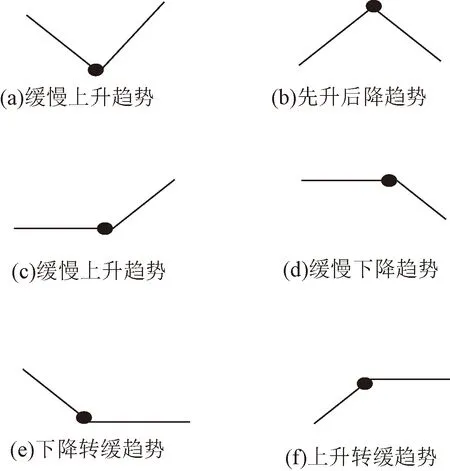
图6 趋势转折点Fig.6 Trend turning point

2.2 聚类量化分析

从以上分析可知同一参数在不同取值空间内变化趋势不同，不同参数对校核指标的影响区间长度不同。为确定参数的敏感范围，需对变化趋势相似的仿真结果进行聚类研究，以分割敏感与非敏感区间。

将数据空间分割为一系列互不重叠的子序列，并且子序列的区间长度存在差异，使得子序列内的数据元素变化趋势相近。传统的系统聚类均是面向无次序关系的数据集不适用于研究，连续空间的动态聚类分析可以基于特征点、基于斜率变化、基于面积变化对连续空间进行分类[18]，可以作为研究的分析方法。在实验结果中，数据轻微的波动不影响数据整体趋势，因此数据轻微波动是允许存在同一影响范畴内。而既有连续空间动态聚类分析容易忽略在更大范围内相同或相似趋势的合并，提出一种基于特征点与波动界限的数据聚类方法，以此来寻找趋势变化特征点。趋势变化点具体寻找流程如下。

步骤1为方便对数据的观察分析，将数据进行归一化预处理，公式为

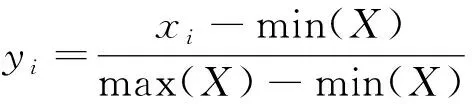
(1)

式(1)中：yi为每个数据xi的归一化结果；X为样本数据；min(X)为样本数据的最小值；max(X)为样本数据的最大值。

步骤2对于连续序列数据xi，对每个数据xi计算方差值，即xi+1-xi，保存到集合A中，即Ai=xi+1-xi，i=1,2,…,n-1。

步骤3依据阈值计算公式计算上升波动U和下降波动D。波动阈值计算公式[19]为

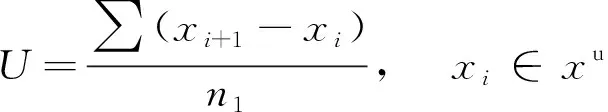
(2)

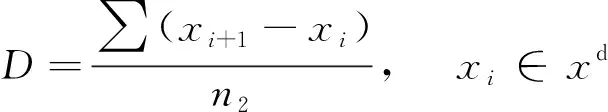
(3)

式中：n1为A中Ai>0的个数；n2为A中Ai<0的个数；xu为Ai>0的数据集；xd为Ai<0的数据集。

步骤4寻找极值点。当数据保持上升趋势时，Ai≥0，且Ai不连续为0，向前搜索，若出现下降点xd，即Ai-1<0，则波动范围val=val+Ai-1，初始val=0。当val0，则波动范围val=val+Ai-1，初始val=0。当val>U，则停止搜索，并在搜索中寻找最小点作为右侧边界点。

步骤5寻找拐点。当|Ai|≤1，且∑i≥n/10时，则认为出现拐点，则第一个方差值小于1的点即为拐点。

步骤6将寻找出的极值点和拐点从小到大依次排序即该连续序列的数据分段点。

由于参数不同取值空间对应的仿真结果的波动情况不同，为量化研究仿真结果的波动情况，因此本文采取基于空间连续序列数据聚类与信息熵的方法对参数敏感区间进行分析研究。信息熵指标来度量本段影响程度。信息熵是信息量大小的度量，是度量样本集合纯度的一种指标[20]。样本纯度越大，数据分布越集中，信息熵越小。分析各样本仿真结果信息熵变化情况，确定信息熵阈值，当信息熵小于该阈值时则认为波动较小。假设当前样本集合B中第k类样本所占的比例为pk(k=1,2,…,|y|),其中y为样本数据集数量，则B的信息熵定义为

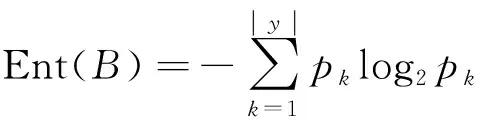
(4)

2.3 结果分析

以参数CC1仿真结果为例。通过对参数CC1的仿真结果进行连续取值空间数据聚类，使每段的数据变化趋势大致相同，最终确定了8个趋势转折点，其中0.45、0.55、1.05、1.45、1.95、2.55、3.10为极值点，3.65为拐点，仿真结果聚类情况如图7所示。可以看出仿真结果聚类后每段数据变化趋势相似，且可以很好地保持原数据的变化特性。

为判断参数CC1变化对校核指标延误影响的曲线波动情况，以上述分段结果作为样本长度计算各段的信息熵，各段对应的信息熵如表3所示。由于(0.50,0.55)中包含两个数据，计算此区间信息熵无意义，因此忽略此段信息熵的计算。由表3可知，(0.05,3.65)区间内各段信息熵均大于2，区间(3.70,5.00)信息熵为0.92，与其他区间内信息熵相差较大，结合图7，区间(3.70,5.00)内的波动比较小，数据基本稳定，因此认为(3.70,5.00)区间内参数CC1对校核指标延误不敏感。最终确定参数CC1的敏感区间为(0.05,3.65)。由以上分析可知当信息熵小于1时，曲线基本稳定，因此选取信息熵1为阈值，当信息熵小于1时则认为参数对校核指标不敏感。

表3 各区间信息熵Table 3 Information entropy of each interval

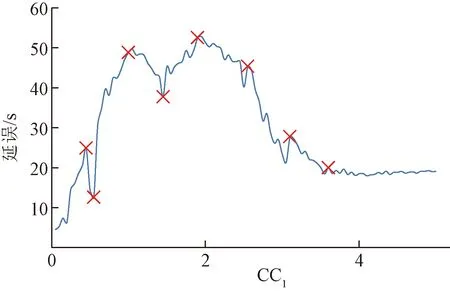
图7 参数CC1数据分段Fig.7 Data segmentation of parameter CC1

通过以上分析步骤，分别对20个驾驶行为参数进行敏感性分析。通过观察参数图像变化趋势以及对数据进行基于连续序列数据的分段的计算，发现在信息熵均大于1的情况下，有些参数并非仅存在单一区间，在合理区间范围内有若干个相似子区间均可取得峰值和谷值，比如参数CC5，参数化CC5在区间(0,2)上信息熵均大于1，且存在若干相似子区间，因此，为减少后续标定工作的计算量，选取其中一个子区间即可。

敏感性参数范围的选取总结概括为两类：一类为在合理的取值区间内存在对校核指标有影响的一个区间，例如参数CC1、CC7、CC8、ACCX、ACCmax等；第二类为在合理的取值区间内有多个对校核指标有影响的相似子区间，这种情况下，在合理区间内选取其中一个可取得峰值和谷值的区间即可，例如参数CC4、CC5、Pobd等，最终得出敏感参数集与参数敏感区间。选取参考文献[11，15]中标定参数集及取值范围与研究结果进行对比，如图8和图9所示，可以发现所确定的敏感参数及参数范围与以往研究有所不同，且所确定的敏感参数更加全面。

图8 各个参数取值范围对比Fig.8 Comparison of value ranges of various parameters

图9 Pobd参数取值范围对比Fig.9 Comparison of Pobd parameter value range

3 结论与展望

参数敏感性分析是微观仿真模型标定的关键步骤，准确地选取待标定参数集以及参数的取值范围是提高微观仿真模型参数标定结果可移植性的潜在前提，但在标定的过程中参数集和参数范围的选取具有一定的盲目性，不同的敏感性分析工作，在对相同的交通设施进行标定时会使标定结果出现很大的差异。通过VISSIM仿真平台进行实验，基于变化趋势，提取趋势变化点，将仿真结果按照变化趋势进行聚类分析。进而利用信息熵法定量分析仿真结果每段变化幅度。得到如下结论。

(1)通过分析确定了信息熵阈值为1，当信息熵小于1时则认为参数区间对校核指标延误不敏感。

(2)通过对仿真结果变化趋势分析，发现存在多个相似敏感子区间的参数，例如参数CC5，为减少标定工作量，敏感区间仅取其中一个敏感子区间即可。

(3)通过聚类量化方法可以精确的确定敏感参数及其范围，排除了因实验范围选取不合理造成参数敏感性分析不准确的情况。

虽然本文对象只是针对快速路的交织区场景，但研究方法及结果可以推广到不同的仿真对象，为参数集和参数范围的选取提供科学理论基础，在以后的研究中可直接在本文参数敏感范围基础上进行研究。仿真模型参数标定的最终目的是对参数进行校正求解，使模型更加符合仿真对象的实际运行情况。因此本研究仅是前序工作，是参数优化的基础，在本研究的基础上将会进一步研究，求解出模型的合理参数值。