不同厚度充填体-围岩组合体力学性质及损伤本构

李胜， 熊自明， 刘一鸣， 李志浩

(陆军工程大学爆炸冲击防灾减灾国家重点实验室， 南京 210007)

在地下矿产开采中，通常采用由尾砂、水、硅酸盐水泥配制的胶结充填体对采空区进行回填支撑采场周围岩体，形成共同承载的充填体-围岩层状组合体。可以有效改变围岩中的次生应力场，降低岩体应力能量释放速度，减轻采场围岩的变形和片落，预防采场冲击地压与变形的发生[1-3]。但充填体-围岩层状组合体所处环境复杂，在高地应力条件下，组合体仍存在失稳风险，造成大规模的巷道崩塌或冲击地压，造成巨大的经济损失[4]，因此研究在荷载作用下充填体-围岩层状组合体的损伤演化规律，对评估深部采场的稳定性至关重要[5]。

鉴于充填体-围岩层状组合体的重要性，科研工作者进行了大量研究。在理论研究方面，汪杰等[6]针对水平分层充填体，基于全微分方法提出了考虑分层效应的充填体强度准则。王旭一等[7]结合基于 Weibull 分布的二维非均质线性平行黏结模型和非均质光滑节理模型，提出了一种新的层状岩体细观非均质接触力学模型，探究层面均质度、间距、倾角对层状岩体力学特性的影响；史越等[8]结合柯西转轴方程和随机损伤理论建立了一种考虑荷载损伤的本构模型，揭示了单轴压缩条件下层理倾角变化对岩体力学性质的影响，并利用炭质千枚岩进行单轴压缩试验验证了模型的准确性。程爱平等[9]进行单轴压缩下充填体-围岩组合体的声发射试验，并基于累积声发射振铃计数构建组合体损伤本构方程。侯永强等[10]开展了处于不同养护龄期下的充填体的单轴压缩试验，并建立了考虑养护龄期的分段式损伤本构模型。

在试验研究方面，宋卫东等[11]开展了充填体-围岩组合体的侧限压缩试验，指出加载过程中组合体破坏模式由拉伸破坏向剪切破坏转变。赵康等[12]利用两种不同灰砂比组合体进行单轴压缩试验，指出组合体的整体峰值强度取决于灰砂比较小的试件。刘晓云等[13]利用水泥、砂和石膏作为相似材料制作不同强度材料组合试件进行单轴压缩试验，指出组合体整体强度受较高强度材料体积占比的变化的影响较为显著。曹帅等[14]制得不同灰砂比三分层柱状组合充填体试样并进行单轴压缩试验，指出破坏时组合体主要表现为中部首先发生破坏，顶部和底部伴随拉伸和剪切破坏。柴少波等[15]分析了充填节理岩样在累积冲击作用下损伤演化规律，指出充填节理岩样在累积损伤后动力强度不断降低，且降低程度与充填材料和充填厚度相关。

在充填开采过程中，充填厚度不同，对整体的协同变形机制与围岩支撑效果影响较大。针对厚度变化对整体性能影响规律研究，在前人研究的基础上，现采用相似材料制作不同厚度水平状充填体-围岩组合体模型进行室内单轴压缩试验，结合数字散斑技术(digital image correlation，DIC)，分析在破坏过程中试样表面应变场变化，探究含不同厚度充填体试件的力学特性与损伤破坏演化特征的差异。同时建立考虑峰后应变软化特征的分段式损伤统计本构模型，对因充填引起的初始损伤与因加载引起的损伤变化进行分析，利用试验实测数据与文献数据对模型进行验证。以期为充填厚度不同的采矿工程的稳定性分析和设计提供理论方面的参考。

1 试验过程

1.1 试件制备

充填体-围岩层状组合体具有多相不均匀性、各向异性与层间界面力学性质，在选择模型材料时其力学性质应与工程实际相近。在张波等[16]、张桂民等[17]、赵康等[18]学者的研究结果的基础上，结合钻孔触探实验室与井下测试数据[19]，选用砂岩与质量比为4∶1.5∶1.5∶1的细河沙、P·Ⅱ52.5硅酸盐水泥、硫酸钙白粉、水的砂浆制作试件。其中，砂岩为深部矿场中常见的岩体，相较现地开采岩样，试验选用的砂岩受开采扰动较小，质地更为均匀，离散性小；砂浆为常用充填体材料，可与砂岩充分胶结，且充分振捣后内部缺陷更少。

考虑到选用方形试件利于图像采集与应变场分析。采用浇筑方式制成100 mm×100 mm×100 mm立方体试件。首先在100 mm×100 mm×100 mm亚克力模具内对称放入一定厚度的红砂岩作为围岩层，红砂岩中间预留空间；随后将按比例调配的水泥砂浆填入预留空间，同时不断用橡胶锤敲击模具，使得水泥砂浆均匀充填；最后将充填好的试样放入振捣机充分振捣5～10 min，确保砂浆内空气充分排出，保证试样均匀性，将振捣后的试样置于恒温箱(温度19.9 ℃，湿度97%)中养护7 d后进行试验。按照上述方法，根据充填体厚度不同共设计0、10、30、50、100 mm共5种不同工况，其中0 mm试样为完整红砂岩试件，100 mm试样为完整水泥砂浆试件。为保证试样的均匀性，选用产自山东日照的同一批次红砂岩，水泥砂浆严格控制材料用量、搅拌时间、振捣时间，防止因试验条件差异导致试验结果离散。

图1(a)为模型试件图像。为防止因试验数量较少而导致测量结果离散化，每种工况进行3组对比试验，共15组有效试验。如图1(b)所示，试验前在试件表喷涂随机生成的散斑，在试验过程中利用便携式工业相机记录，并利用数字散斑技术分析试件表面应变场变化。

H、h分别为红砂岩层与水泥砂浆层厚度图1 模型试件及随机散斑Fig.1 Model specimen and random speckle

1.2 试验设备与过程

试验设备分为加载系统与测量系统。试验采用准静态单轴压缩加载方式，加载系统采用HUT160D微机控制电液伺服万能试验机，规格为1 000 kN，准确度等级为0.5级，在试验中均采用力控制方式进行加载，加载速率为500 N/s。测量系统包括便携式工业相机与图像收集系统，设置图像采集速率为1 帧/s，图像分辨率为 2 488 pixel×2 048 pixel，灵敏度约为0.01个像素大小。试验前，调节便携式工业相机位置与镜头焦距，保证图像采集质量满足精度要求；试验开始后，同步开始拍摄与加载，直至试件破坏，停止加载并收集图像。

试验设备布置如图2所示。

图2 试验设备Fig.2 Experimental equipment

2 充填体厚度的影响

2.1 充填体厚度对试件力学参数的影响

根据单轴压缩试验结果，可得含不同厚度充填体试件的应力-应变曲线，如图3所示。在加载速率一定的条件下，随着充填体厚度的增加，试件的抗压强度减小，试件变形破坏过程在充填体厚度不同情况下的阶段特征基本相似，体现充填厚度增加对组合体试件力学特性的损伤作用。利用图3试验数据，分别绘制峰值应力σmax、峰值应变εf、弹性模量Eh随充填体厚度h变化曲线，如图4所示。

σa、εa为线弹性阶段过渡的转折点A对应的应力、应变；σc、εc为峰值点C对应的应力、应变(b)变形全过程示意图图3 应力-应变曲线与变形全过程示意图Fig.3 Stress-strain curve and schematic diagram of the whole deformation process

分析图3、图4曲线变化规律，充填体厚度的增加对组合岩体的力学性质影响显著。充填体厚度为0 mm时(完整砂岩试件)，试件的抗压强度为94.6 MPa，达到峰值应力后出现明显应力跌落；充填体厚度为10 mm时，试件抗压强度下降为56.1 MPa，相较完整砂岩试件下降约40%，达到峰值应力后，应力跌落较小。分析其原因为此时峰值荷载已经超过材料抗压强度，材料性能已经失效，但整体结构未完全破坏，仍有一定承载性能，应力突降相对较小；充填体厚度为30 mm时，试件抗压强度下降为25.4 MPa，此时应力-应变曲线开始出现明显的弹性屈服，呈现弹性变形-连续非线性应变硬化-应变软化形式；充填体厚度为50 mm时，试件抗压强度继续下降为14.8 MPa，试件延性破坏特征更加明显；完整砂浆试件峰值强度为10.1 MPa。分析峰值强度变化规律，充填体厚度的增加显著弱化了组合岩体的整体强度，当达到50 mm后，这种弱化趋势变缓，此时试件强度已趋近于完整砂浆试件强度。对比不同厚度充填体情况下试件的峰值应变与弹性模量，完整砂岩试件峰值应变为3%，弹性模量为3.76 GPa，含10 mm充填体试件峰值应变为2.4%，弹性模量为2.57 GPa，含30 mm充填体试件峰值应变为2.1 %，弹性模量为1.73 GPa，含50 mm充填体试件峰值应变为1.5%，弹性模量为1.55 GPa，完整砂浆试件峰值应变为0.9%，弹性模量为2.01 GPa。随充填体厚度的增加，试件的峰值应变呈单调减小的变化规律，而弹性模量呈先减小后增大的抛物线变化规律，分析原因如下：一是随着砂浆层厚度增加，试件整体强度降低，当应变较小时便开始发生破坏；二是砂浆层与夹板间摩擦力相较高于砂浆层与红砂岩层间摩擦力，因此完整水泥砂浆试件承受层间作用更加明显，表现出更“硬”的现象，相较充填体厚度为50 mm试件，弹性模量存在一定的上升，但由于整体强度较低，在较低应力峰值与应变时便开始破坏。

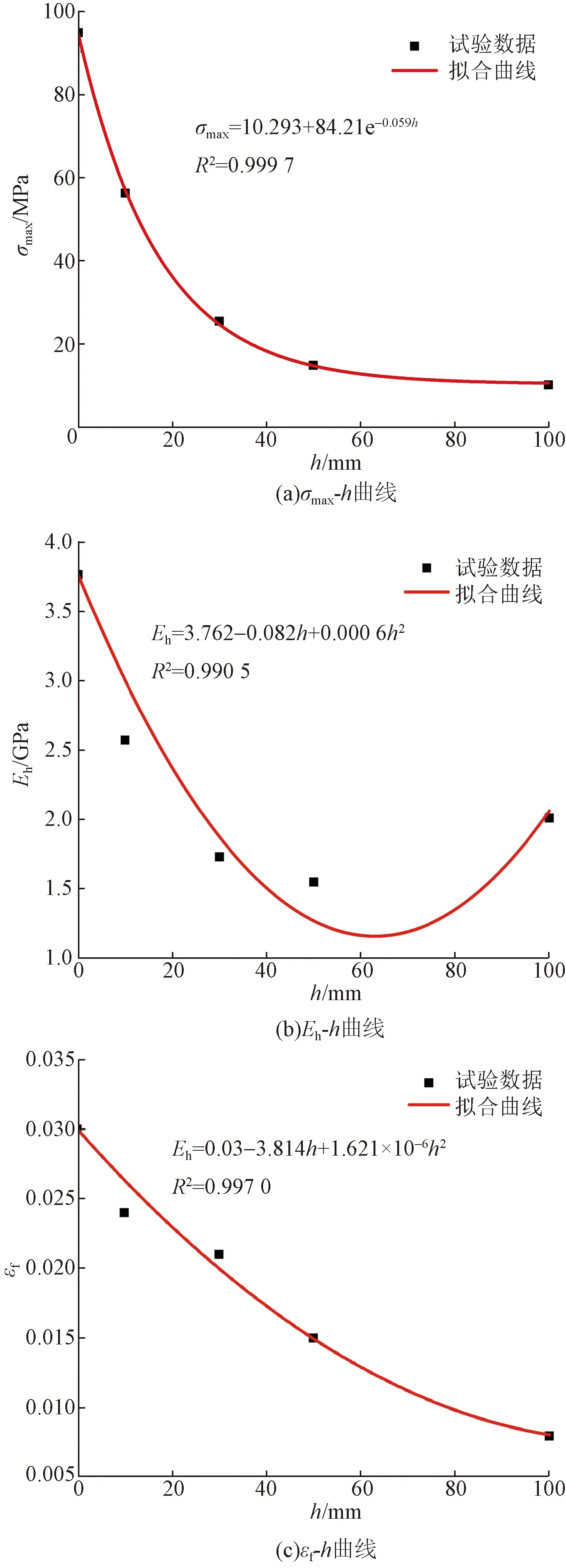
图4 力学参数与充填体厚度的关系Fig.4 Relationships between mechanical parameters and the thickness of backfills

2.2 试件破坏模式分析

组合体单轴压缩全过程应力-应变曲线可分为OA、AB、BC、CD共4个阶段，如图3(b)所示，分别对应初始压密阶段-线弹性变形阶段-塑性变形阶段-峰后破坏阶段的全过程。利用数字散斑技术对水平正应变场进行分析，首先将工业相机获取的图像导入GOM Correlate 软件，经过定义距离-创建平面组件-定义平面坐标系-正应变场分析等步骤，得到试件表面对应水平正应变场演化图如图5、图6、图7所示。

由图5、图6、图7可发现，裂纹均是从充填体开始发育并逐步延伸到砂岩层，最终贯通整个试件。

图5 含10 mm充填体试件表面水平正应变场演化图Fig.5 Evolution diagram of horizontal positive strain field on the surface of specimen with 10 mm filling body

图6 含30 mm充填体试件表面水平正应变场演化图Fig.6 Evolution diagram of horizontal positive strain field on the surface of specimen with 30 mm filling body

图7 含50 mm充填体试件表面水平正应变场演化图Fig.7 Evolution diagram of horizontal positive strain field on the surface of specimen with 50 mm filling body

(1)初始压密OA阶段。试件初始应变场分布都较为均匀；随着应力的增加进入线弹性变形AB阶段，充填体内微裂纹发育，裂纹稳定拓展，含10 mm与含30 mm充填体试件中红褐色拉剪应变局部化带由充填体向上或向下发育，在砂岩层中形成拉伸应变局部化带，相较于含50 mm充填体试件裂纹拓展缓慢，仅存在少许斜向剪切应变局部化带，尚未向砂岩层发育，从图3(a)中可看出屈服点前试件应力-应变曲线基本呈线性关系。因此，屈服点前阶段组合体在荷载作用下的变形可近似视为弹性变形，由荷载增加而产生的损伤变量值可视为 0。

(2)塑性变形BC阶段。含10 mm与含30 mm充填体试件中拉剪应变局部化带加速发展，当荷载接近峰值应力时，第二道水平拉应变局部化带均已在砂岩层中拓展，而含50 mm充填体试件充填体中斜向剪切应变局部化带进一步发育形成X形剪切裂纹，并向上延伸在砂岩层中产生局部拉应变局部化带。

(3)峰后破坏CD阶段。达到峰值应力后，试件失稳破坏，承载力下降，不同工况下破坏模式不同。含10 mm充填体试件破坏时，砂岩中存在竖向拉伸裂纹与斜向剪切裂纹，充填体边缘砂浆压碎剥落较多，综合可判断试件为拉剪复合破坏。含30 mm充填体试件破坏时，试件达到峰值应力状态时上下层砂岩中出现局部张拉裂纹，而斜向剪切裂纹较少，裂纹开展程度较小，进一步加载，试件沿裂纹拓展使得整体失稳破坏，具有明显延性破坏特征，综合可判断为从充填体开始的劈裂破坏；含50 mm充填体试件破坏时，试件峰值应力很低，上下砂岩层中仅1～2道竖向张拉裂纹，充填体中存在X形剪切主裂纹并与砂岩层中张拉裂纹相连，综合判断试件是从充填体开始的劈裂破坏。

试件的破坏模式受层间作用[20]的影响较大，在承受轴向荷载时，砂岩与充填体变形能力不同，上下层约束不协调，充填体率先变形起裂，进而导致砂岩中产生沿垂直方向的拉伸裂纹。随着充填体厚度的增加，此时加载状态类似于刚性板直接加压完整砂浆试件，充填体内部发生X形剪切破坏，进而引起整体破坏。

3 考虑峰后应变软化阶段的损伤本构模型

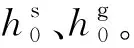
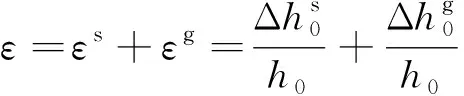
(1)

式(1)中：εs、εg分别为岩石骨架部分与空隙部分的应变。

如图3(b)所示，假设岩石骨架在压密阶段发生弹性变形，满足广义胡克定律且线弹性变形阶段试件已经被压密，则可忽略微小波动，对线弹性变形阶段进行回归分析，表达式为

σ=Eε-c

(2)

得到的直线斜率即为试件弹性模量E，拟合直线与试验曲线交点可定为压密阶段向线弹性阶段过渡的转折点A与屈服点B，拟合直线与坐标横轴的截距c/E即为在压密阶段试件空隙部分总应变Δεa。

3.1 损伤变量模型

根据 Lemaitre 提出的应变等价原理，综合考虑损伤变量D由充填体厚度变化引起的损伤变量Dh与轴向荷载作用引起的损伤变量DS耦合得到[23]，即

D=Dh+DS-DhDS

(3)

式(3)中：Dh、DS为耦合项，它总是使得总损伤变量D减小。根据宏观唯象损伤力学概念，利用不同充填体厚度情况下弹性模量的差异来表示试件因充填体厚度变化而受到的损伤Dh，表达式为

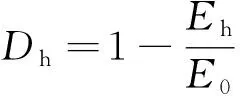
(4)

式(4)中：Eh为软岩层厚度为h的试件的弹性模量。

从宏观角度DS可定义为已损伤单元数Nf与总单元数Nt的比值，即

将采收后的大葱就地薄而均匀地铺在沟间，经风吹日晒后，使茎株的泥土脱落，待葱白表层呈半干状态，然后扎成重7～10千克的葱捆，再一捆捆地直立排列在地势高燥有见光能遮雨的地方晾晒，每隔半月翻检一次，以防腐烂。冬天气温下降至冰点时，移入地窖贮藏。贮藏过程要加强管理，每隔一定时间，打开葱捆查看，如有发热腐烂要及时剔除，如发现潮湿现象，可及时通风调节或将葱搬到日光下摊晒，然后再入窖。

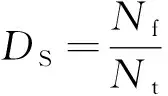
(5)

考虑到初始缺陷的随机性和非均匀性，试件应力-应变曲线为典型的稳定断裂传播型曲线[24]，采用幂函数分布模型描述岩石微元强度F的分布规律，可较好地描述岩石全过程变形破坏关系曲线。曹文贵等[25]指出在线弹性阶段，荷载增加不会使岩石发生损伤，只有达到屈服阶段，荷载增加才会使得岩石发生损伤。同时对于水平层状岩体这类准脆性材料，F采用应变ε表示可以较好地度量破坏全过程中的损伤演化情况。因此，假设在线弹性变形阶段，忽略荷载增加产生的损伤[26]，则微元强度F的概率密度函数的P(F)为

(6)

式(6)中：F为微元强度分布变量；m、S0为分布参数；h为B点对应应变。

进而可认为轴向荷载作用引起的损伤变量h在屈服点B之后也满足幂函数分布规律，则DS的表达式为

(7)

考虑到试件破坏后仍然存在一定的残余强度，引入荷载损伤修正系数q对荷载作用引起的损伤变量DS进行修正，最终得到损伤演化模型如式(8)所示。

(8)

3.2 岩石损伤本构模型建立

假设组合体试件在线弹性变形阶段符合广义胡克定律，得到损伤本构模型[27]，如式(9)所示。

[σ]=E0εs(1-D)

(9)

式(9)中：D为损伤变量；[σ]为有效应力；E0为完整砂岩弹性模量；εs为岩石骨架应变 。综合式(1)、式(8) 、式(9)，得到考虑后续损伤阶段的分段损伤本构模型为

(10)

式(10)中：εa为A点对应应变。由于压密阶段对分析试件全过程变形关系影响较小，当ε≤εa时，可直接连接OA，近似模拟压密阶段，拟合结果表明这种方法对分析结果无影响。

3.3 理论模型验证与讨论

为说明所推导的不同充填体厚度试件分段损伤本构模型的正确性与合理性，将试验参数代入损伤本构模型，绘制模型曲线并与5种不同厚度充填体试件的试验曲线进行对比。表1为损伤本构模型的参数值。

表1 损伤模型参数Table 1 Parameters of statistical damage model

将上述试验数据代入式(10)计算得出含充填体试件分段损伤本构模型理论曲线如图8所示。在峰前阶段，不同工况下的试验曲线和理论曲线呈现较好的一致性，在峰后应力跌落阶段，试验曲线与理论曲线的峰值应力和峰值应变的数值基本一致，体现所建立模型的合理性。在残余强度阶段，随着变形的进一步发展，试件仍然具有一定的承载能力，从理论曲线和试验曲线的变化趋势来看，理论曲线较好地表征试件变形破坏过程的阶段特征。

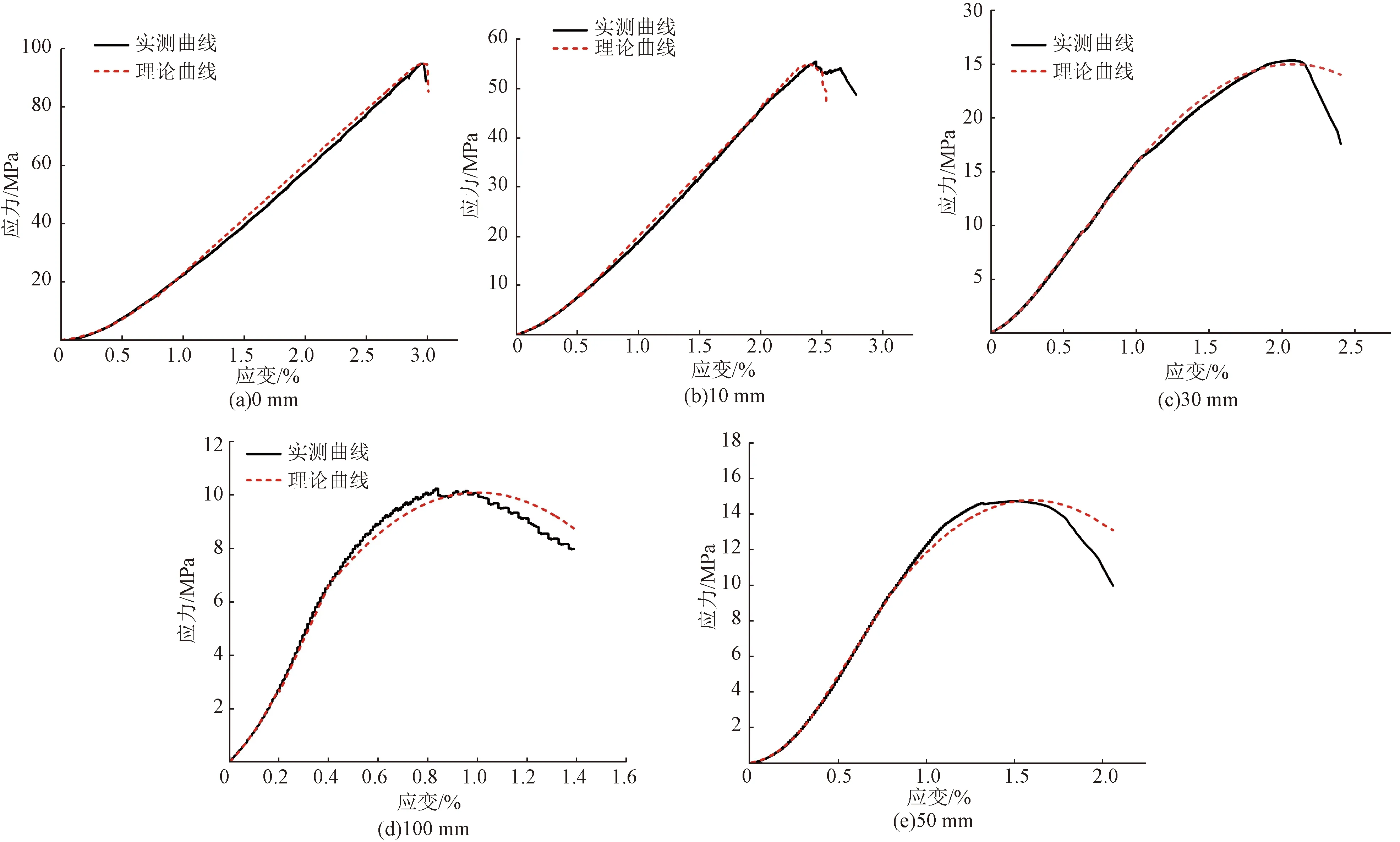
图8 模型计算曲线与试验曲线的比较Fig.8 Comparison between model calculation curves and experimental curves

为验证本文模型的准确性，利用文献[28]单轴压缩试验数据对模型进行验证。文献[28]采用一种与天然赋存的含夹层盐岩单轴力学性能相似的相似材料制得模型试件，其中夹层厚度分别为10、15、20 mm，与所研究工况较为吻合，可以用于模型验证。表2为对应损伤模型参数。

表2 文献[28]损伤模型参数Table 2 Parameters of statistical damage model of literature [28]

将文献[28]参数代入本文模型，得到理论计算结果与试验曲线对比结果如图9所示。应用效果较好，证明本模型对于描述含不同厚度充填体-围岩层状组合体试件的变形破坏过程具有较好的适用性。

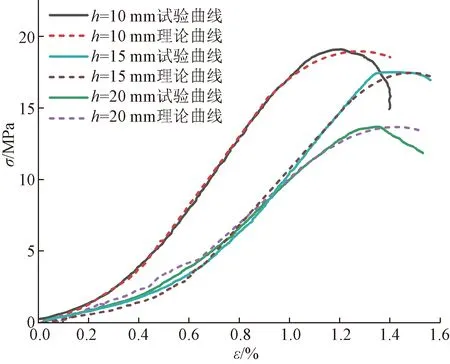
图9 文献[28]理论计算曲线Fig.9 Theoretical calculation curves of Literature [28]

4 损伤变量演化

将表1中试验参数代入式(8)，得到不同充填体厚度情况下总损伤变量D的演化曲线如图10所示，为便于表述，取应变ε与峰值应变εf比值作为横坐标。由图10可知，随着应变增加，开始时不同厚度充填体试件总损伤量保持不变，此时为初始压密与线弹性变形阶段；随着应变进一步增加，总损伤量近似呈线性单调递增。充填体厚度越大，由充填体引起的初始损伤越大。

图10 不同厚度充填体-围岩组合体的损伤演化曲线Fig.10 Damage evolution curve of backfill-surrounding rock combination with different thickness

充填体厚度为0 mm与10 mm，由充填体存在而引起的初始损伤相对较小，分别为0与0.295。当应变达到峰值应变的90%时，总损伤量才迅速上升，这与各自应力-应变曲线相对应。它们的应力-应变曲线均无明显屈服点，在峰值应力前，应力-应变曲线近似为直线；达到峰值应力后，应力突降，表现在总损伤量上便是保持初始损伤不变，当接近峰值应力时，总损伤量突然上升并达到1，试件崩碎。

充填体厚度为30、50、100 mm时，由充填体存在而引起的初始损伤相对较大，分别为0.539、0.587与0.465。它们的屈服点较为明显，当应变达到峰值应变的50%时，试件开始屈服，总损失量开始呈线性上升，当达到峰值应力时，总损伤量未达到1，表明微元单位破坏后承载能力并未完全失去，仍能够承受部分压应力和剪应力，对应于应力-应变曲线峰后存在应变软化，未发生应力突降。

充填体厚度的增加使得试件变形过程中微元的损伤程度差异明显。由图10可知，软弱夹层厚度越大，对应峰值应变越小，即达到相同的总损伤变量D时，充填体厚度越大的试件所对应变形越小，试样更快出现破坏。当总损伤变量D达到 0.75，充填体厚度h为 0、10、30、50、100 mm的试样对应的轴向应变分别为 3.30%、2.64%、2.39%、1.76%、1.12%，表现出随着充填体厚度h增大而逐渐减小。

5 结论

针对充填体厚度变化对充填体-围岩组合体的力学特性与损伤演化特征影响的问题，利用砂岩-砂浆模拟试件，结合数字散斑技术开展了分析探究，并建立考虑峰后应变软化特征的分段式损伤本构模型，得到结论如下。

(1)充填体厚度变化对试件力学性能有显著影响。试件峰值强度随着填充体厚度增加呈指数式下降，峰值应变随充填体厚度呈抛物线式单调下降，弹性模量随充填体厚度增加呈抛物线式先减小后上升的规律。总体来看，充填体厚度的增加对组合体的力学性能是不断削弱的。

(2)通过DIC数字散斑技术分析试件表面应变场变化，充填体厚度增加，对试件破坏模式影响较大。随着充填体厚度增加，破坏模式由完整砂岩试件的脆性剪切破坏过渡到拉剪复合破坏，最终发展为充填体内部发生X形剪切破坏而引起的拉伸劈裂破坏。

(3)建立考虑空隙压密与峰后应变软化阶段的分段式损伤本构模型得到的应力-应变曲线与实测曲线吻合程度高。通过对比分析不同数值模型参数q和m，q主要影响试件峰前塑性变形与残余变形的趋势，m反映峰值应力与残余强度的数值大小，综上所述，参数q和m共同决定了所建立模型的变化趋势与理论数值大小。

(4)充填体厚度越大，由充填体存在而引起的初始损伤越大，试件变形过程中微元的损伤程度越明显。表现在总损伤变量D相同时，充填体厚度越大，对应所需轴向应变越小。同时充填体厚度越大，达到峰值应变时，损伤变量D未达到1，试件延性破坏特征越明显，破坏后残余强度越高。

因此，为确保在复杂地应力、开采扰动等因素的影响邻近采场及矿柱的安全，采空区较大时回填后仍应进行一定的支护，避免因开采过程中的应力突变而引发工程灾害。