岛礁三维SWASH模型的时空敏感性分析

陈汉宝，钟 生，陈松贵*，时 健

(1.交通运输部天津水运工程科学研究所，天津 300456；2.河海大学 港口海岸与近海工程学院，南京 210098)

珊瑚礁主要是由珊瑚虫、钙化藻、有孔虫等造礁生物的灰质骨骼残体世代堆积形成。我国的珊瑚礁主要分布于中国大陆南方沿岸、海南岛和台湾岛[1]，以及南海的西沙、东沙、中沙和南沙群岛。珊瑚礁生态系统为人类社会提供了多种多样的服务，发挥着重要的作用，如海洋生物资源、渔民生计、建筑材料和海洋药物以及文化旅游娱乐等。因此，如何在维持原有生态环境情况下提高珊瑚礁系统的多样性，就需要对珊瑚礁地形上的水动力特性有充分的了解和研究[2]。

由于珊瑚礁地形是一种坡度急剧变化的陡变地形[3]，在此类复杂地形条件下，研究波浪在珊瑚岛礁地形上的波高、流速、增减水等变化规律，对珊瑚礁系统的生态环境保护和利用起着至关重要的作用。目前针对珊瑚岛礁地形下的波流研究主要方法包括：现场观测、物理模型试验和数值模拟等。对于现场观测而言，通常只能针对特定区域或测站，并且投入时间长、资金多，同时极易受到自然因素的影响。另外，物模试验的试验设计以及试验开展需要投入较多的人力、物力和财力等，还可能会受到场地限制和试验材料等因素的影响，并且模拟的试验工况也会相对受限，特别是极端工况下的水动力模拟非常困难。为了获取更多类别及工况的试验数据，开展数值模拟试验既能解决以上所面临的问题，还能够节约大量的试验成本。

随着计算机性能的不断提高，计算方法的不断进步，促进了波浪数值模拟技术的研究与应用的发展[4]。其中，非静压波浪模型得到快速发展，其中基于非线性浅水方程的非静压波浪模型SWASH，采用单值函数对自由表面进行追踪[5]，可以对较为复杂地形下的波面和浅水流进行大范围、长时间的模拟。并且，Suzuki等[6]通过SWASH模拟结果与试验数据的对比，验证SWASH模型在波浪变形和越浪计算的适用性；Guimaraes等[7]通过SWASH对巴西Tramandaí海滩波浪进行了模拟，并对其爬坡模拟值进行了验证，得出SWASH可以很好地模拟该海域的波浪状况。白志刚[8]对基于Boussinesq方程的FUNWAVE模型和基于非线性浅水方程的SWASH模型从计算精度和运行速度等方面进行分析对比，得出SWASH模型比FUNWAVE模型更具有实用性；王良才等[9]将SWASH模型模拟结果与物理模型的实测数据进行对比后发现，SWASH模型可以对近海岸及港口区域的多种物理现象如浅水变形、绕射、折射、反射、破碎等现象进行有效的模拟。不过，诸多涉及SWASH模型的文章并没有特别关注SWASH模型模拟下空间步长和时间步长的变化对试验结果的影响，因此本文将采用SWASH模型对岛礁进行三维模拟，并选取不同的空间步长和时间步长模型模拟的试验数据进行SWASH模型的时空敏感性研究。

1 非静压模型SWASH简介

1.1 控制方程

SWASH (Simulating Waves till Shore)模型由代尔夫特理工大学的Stelling、Zijlema和Smit等学者开发完成的一款浅水非静压数值模型[10-12]。模型考虑了波浪运动中的非静压影响，适用于深海至浅水条件下波浪和水流运动的模拟，特别是对于复杂地形如三维地形下的波浪破碎所引起的波浪增水和波生流有着较好的适用性。特别地，SWASH的控制方程里特别考虑到垂向动量方程和水平动量方程中附加的非静压项，在求解时把控制方程分解为静压项和非静压项两部分分别求解[13]，其控制方程如下

(1)

(2)

(3)

(4)

式中：t为时间；x、y和z方向的速度分量分别为u、v、w，水平向粘滞系数为vH，垂向粘滞系数为νv。ξ代表自由面；g代表重力加速度；q代表非静水压力。

1.2 边界条件

自由面的压力边界条件为

q|z=ξ=0

(5)

当垂向流速满足式(5)的边界条件时水平流速满足

(6)

在SWASH中关注入流边界位置，其边界条件的设定，需要明确速度参数，同时考虑弱反射问题

(7)

式中：ub为入流边界的流速；边界入射波的波幅由ξb表示；式(7)中边界位置是通过正负号来描述的，+号表示入流边界为西、南边界，-号表示入流边界为东、北边界。并且采用干湿处理技术来描述动边界，模型通过给定最小水深值限制网格点计算过程中出现的负水深，在计算的单位时间步长内对网格点进行干湿判断，当计算的网格点水深低于最小水深时，将最小水深设为该网格点的水深，避免模型计算中出现负水深引起模型运行中断。

1.3 数值求解

SWASH模型计算采用有限差分格式进行空间离散，垂向采用σ分层网格，变量通过交错网格方式布置。非静水压力q定义在单元边中心，如图1所示。

图1 网格垂向分层和变量布置示意图Fig.1 Schematic diagram of grid vertical stratification and variable layout

2 物理模型简介及数模参数设置

2.1 物理模型简介

图2 模型尺寸及试验仪器设置Fig.2 Model size and test instrument setting

整体物理模型建于交通运输部天津水运工程科学研究院综合试验厅的波浪水池中，水池长60 m，宽42 m，深1 m，水池一侧的造波系统由9台推板式造波机和微机控制系统组成。在距造波机34 m处设置坡度为1:8的斜坡模拟礁前斜面，水平投影长3.2 m，斜面后接长度为14 m的水平平台模拟礁坪，其顶高程为0.4 m。在两个礁坪中间存在宽度为6 m的裂口，礁坪后存在宽度为5 m的潟湖，最后在潟湖后设置坡度为1:3.3的礁后斜坡，其余斜坡坡度均为1:1。物理模型底部用砂石填充，表面进行光滑水泥抹面。试验中采集波面使用的是LG1型电容式浪高仪，浪高仪量程为0.6 m，绝对误差小于1 mm，采集单点流速分布使用的是ADVs(超声多普勒流速仪)和螺旋桨式流速仪。由于该礁坪-潟湖-裂口系统物理模型对称分布，因此所有的仪器主要布置在裂口的一侧。具体的试验模型尺寸和试验分析所用到的仪器编号位置如图2所示，其中G3、G5等表示波高仪布设位置，1#、2#、3#，ADV1、2，LXJ-1、3等表示流速仪布设位置。

2.2 SWASH模型参数设置

根据邹国良等[14]的研究，在模拟波浪传播时，非静压模型的水平网格选取ΔX=L/30便可较为精确地模拟波面、流速等结果。本文选取物理模型一组特征工况为：礁坪淹没水深hr=0.04 m，外海入射波高H0=0.04 m，周期T0=2 s，通过计算可得到波长L=3.847 m，因此选用模型网格尺寸为ΔX=0.1 m，ΔY=0.1 m。波浪入射为垂直左边界入射，在右边界处设置5 m宽的海绵层，模型垂向取4层，糙率通过设置曼宁粗糙系数实现。考虑到计算网格尺寸会影响到模型的空间分辨率，因此本文以模型网格尺寸为上限，选取精度介于Δx=L/100～L/30间的七组不同计算网格尺寸0.04 m、0.05 m、0.06 m、0.07 m、0.08 m、0.09 m、0.1 m进行模拟研究，并将模拟数据进行分析对比。此外，SWASH使用手册提到SWASH中的时间步长应足够小，以解决计算出波场本身的时间变化，因此选取介于0.005～0.03 s的0.005 s、0.01 s、0.02 s、0.03 s四组不同计算时间步长进行模拟研究，以此来分析模型值随计算网格尺寸和计算时间步长的敏感性变化。

3 敏感性分析及方法简介

本文主要选取与物模流速测点和礁坪中线对应位置的平均流速和有效波高进行敏感性分析，现针对本文数学模型所用的敏感度分析法做如下简介：

3.1 流速随计算网格尺寸的敏感性变化

图3展示了不同计算网格尺寸、计算时间步长均为△t=0.01s下裂口中线和礁坪中线在x方向各测点数值模拟和物理模型的向岸平均流速，平均流速取造波稳定后30个周期内的平均值。通过对比可以发现，当△x在0.04 m附近时，这三个测点位置向岸平均流速吻合度最高。对比礁坪上测点的向岸平均流速也可以发现，各个测点的数值模拟值与实测值吻合度也较好，在礁坪上数值模拟值与实测值有微小差距，分析原因在于，波浪传播至礁缘处时，波浪发生破碎，波浪形态和流速发生改变，并且实际物理模型与数值模拟的地形条件不可能完全相同，因此模拟结果也会存在相应的差异，不过其最大误差仍在允许范围内。

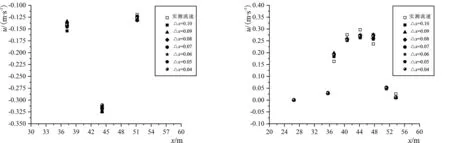
3-a 裂口中线测点平均流速 3-b 礁坪中线测点平均流速图3 不同△x下裂口和礁坪中线测点平均流速Fig.3 Average flow velocity at the measuring points in the middle line of crack and reef flat under different △x

表1 不同△x下各测点向岸平均流速Tab.1 Average velocity of each measuring point towards the shore under different △x m/s

表2 不同△x下各测点向岸平均流速敏感度Tab.2 Sensitivity of shore average velocity of each measuring point under different △x %

3.2 波高随计算网格尺寸的敏感性变化

图4展示了不同计算网格尺寸、计算时间步长均为△t=0.01 s下裂口中心线和礁坪中心线在x方向各测点数值模拟和物理模型的有效波高，波高选取造波稳定后30个周期内的波高值。通过对比可以发现，在裂口通道G39及以前各测点数值模拟的有效波高值与实测值吻合度较好，在潟湖内和靠近礁后斜坡处G40、G41测点的有效波高值随计算网格尺寸的改变也发生变化，并且其影响不可忽略。此外，通过对比礁坪上测点的有效波高值也可以发现，自外海向潟湖内部，各个测点的有效波高值与实测值吻合度也较好，礁坪中部G12测点数值模拟值与实测值有微小差距，在靠近礁后斜坡G15测点的有效波高值随着计算尺寸的改变也发生变化，并且其影响也不可忽略，分析原因在于波浪发生破碎后，波流形态发生紊动，并且礁后斜坡处存在强烈的反射现象，因此物理模型和数值模拟的流速和波高在靠近礁后斜坡处附近存在相应的差异，不过可以发现，当△x在0.05 m附近时，各测点的有效波高值与实际物理模型值吻合度较好。

4-a 裂口中线测点有效波高 4-b 礁坪中线测点有效波高图4 不同△x下裂口和礁坪中线测点有效波高Fig.4 Effective wave height at the measuring points in the middle line of the crack and reef flat under different △x

表3是不同计算网格尺寸、计算时间步长均为△t=0.01 s时各测点有效波高值，波高选取造波稳定后30个周期内的波高值。以最高精度计算网格尺寸△x=0.04 m为基准组，应用敏感性分析方法对不同计算网格精度下所有测点的有效波高值敏感度S(Hsi,xi)=(△Hsi/△xi)/(Hsi,xi)进行计算，其计算结果如表4所示，其中：△Hsi表示每组计算网格尺寸下的有效波高相对于基准组△x=0.04 m的有效波高的差值；△xi表示每组计算网格尺寸与基准组△x=0.04 m的计算网格尺寸的差值；Hsi表示每组计算网格尺寸下对应测点各自的有效波高值；xi表示基准组参数，此处为基准计算网格尺寸△x=0.04 m。由表4可以发现，裂口中线测点G40以前的各测点位置的敏感度都小于10%，潟湖内测点G40和靠近礁后斜坡的测点G41的有效波高值对计算网格尺寸的变化表现得比较敏感，再对比礁坪中线上有效波高值也可以发现，测点G12以前的各测点位置的敏感度几乎都小于10%，测点G12至测点G15，有效波高值也对计算网格尺寸变得比较敏感。分析原因，在复杂三维地形下，低精度网格尺寸在输出时因读取不到相邻网格点间某些较大的数值而导致结果偏小，因此利用非静压模型SWASH模拟近岸复杂地形时，计算网格精度是一个不可忽略的重要因素，高精度的计算网格对模型的准确性起着至关重要的作用。

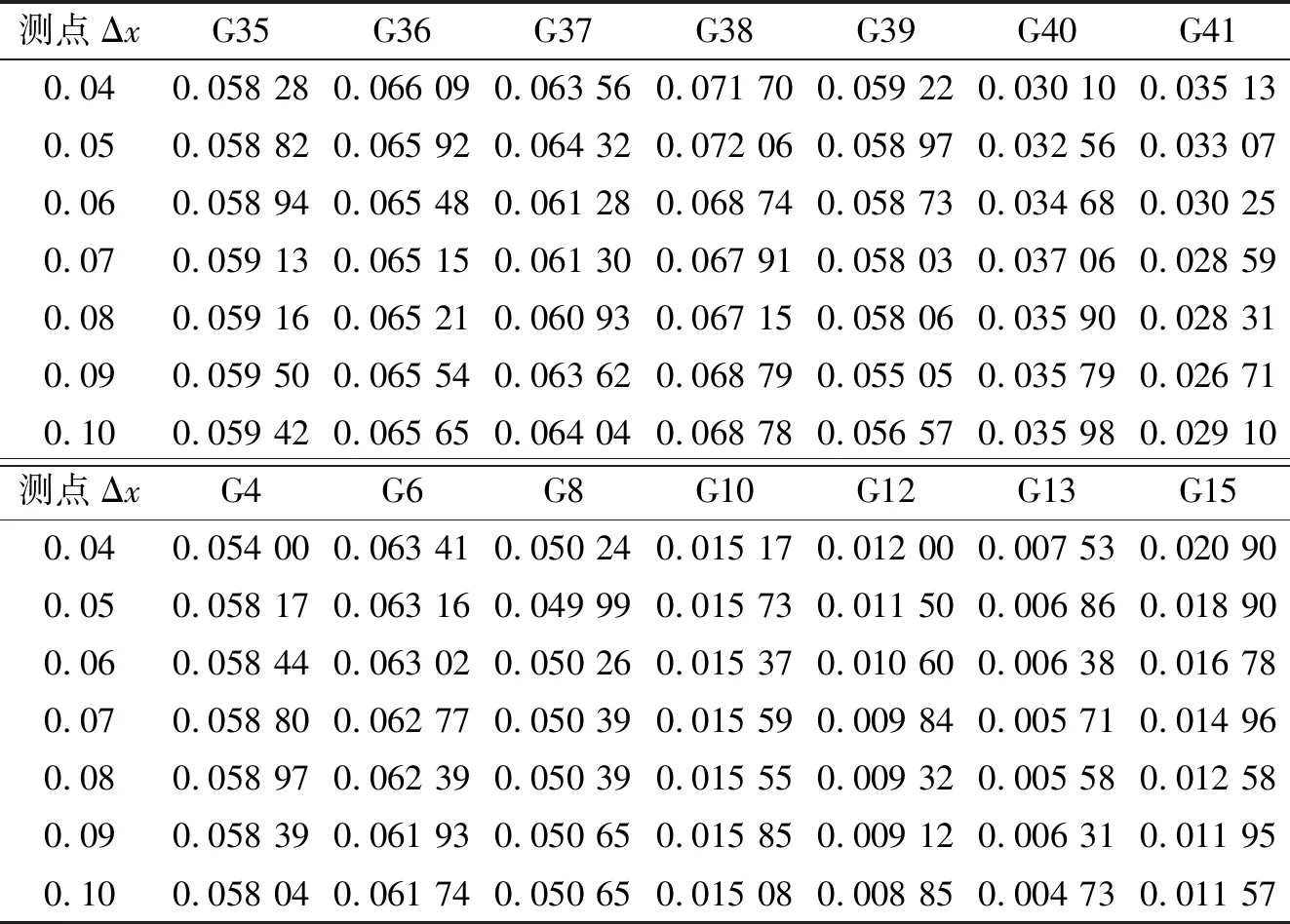
表3 不同△x下各测点有效波高值Tab.3 Effective wave height of each measuring point under different △x m

表4 不同Δx下各测点有效波高值敏感度Tab.4 Sensitivity of effective wave height value of each measuring point under different Δx %

3.3 流速随计算时间步长的敏感性变化

图5展示了不同时间步长、计算网格尺寸均为Δx=0.04 m下裂口中心线和礁坪中心线在x方向各测点数值模型的向岸平均流速。通过对比可以发现，改变时间步长，数值模型的流速值没有明显的变化，其影响可忽略不计。

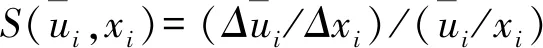
5-a 裂口中线测点平均流速 5-b 礁坪中线测点平均流速图5 不同Δt下裂口和礁坪中线测点平均流速Fig.5 Average flow velocity at the measuring points in the middle line of crack and reef flat under different Δt

表5 不同Δt下各测点向岸平均流速Tab.5 Average velocity of each measuring point towards the shore under different Δt m/s

表6 不同Δt下各测点向岸平均流速敏感度Tab.6 Sensitivity of shore average velocity of each measuring point under different Δt %

3.4 波高随计算时间步长的敏感性变化

图6展示了不同时间步长、计算网格尺寸均为Δx=0.04 m下裂口中心线和礁坪中心线在x方向各测点数值模型的有效波高值。通过对比可以发现，时间步长对有效波高值的影响程度很低，在计算时间步长为0.005～0.03 s，改变时间步长，对模型输出的有效波高值几乎没有影响。

6-a 裂口中线测点有效波高 6-b 礁坪中线测点有效波高图6 不同Δt下裂口和礁坪中线测点有效波高Fig.6 Effective wave height at the measuring points in the middle line of the crack and reef flat under different Δt

表7是不同时间步长、计算网格尺寸均为Δx=0.04 m时各测点有效波高值，波高选取造波稳定后30个周期内的波高值。以最高精度时间步长Δt=0.005 s为基准组，应用上述方法对不同计算网格精度下裂口和礁坪中线上测点的有效波高值敏感度进行计算S(Hsi，xi)=(ΔHsi/Δxi)/(Hsi/xi)，其计算结果如表8所示，其中：ΔHsi表示每组计算时间步长下的有效波高相对于基准组Δt=0.005 s的有效波高的差值；Δxi表示每组计算时间步长与基准组Δt=0.005 s的计算时间步长的差值；Hsi表示每组计算时间步长下对应测点各自的有效波高值；xi表示基准组参数，此处为基准计算时间步长Δt=0.005 s。由表8可以发现，裂口中线测点以及礁坪中线上测点的有效波高值敏感度均小于10%，说明在计算时间步长0.005～0.03 s对模型的有效波高值影响并不显著，其影响可以忽略不计。

表7 不同Δt下各测点有效波高值Tab.7 Effective wave height of each measuring point under different Δt m

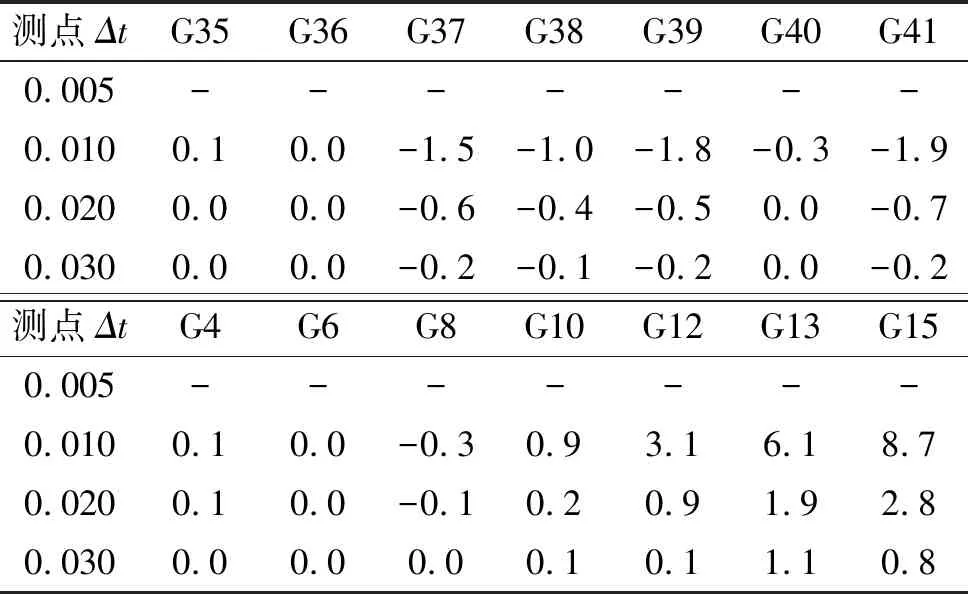
表8 不同Δt下各测点有效波高值敏感度Tab.8 Sensitivity of effective wave height value of each measuring point under different Δt %

4 结论

采用非静压时域波浪模型SWASH，研究了特征规则波工况入射条件下，珊瑚岛礁水域内的平均流速和有效波高随模型中的计算网格尺寸和计算时间步长的变化情况，也可称之为时空敏感性分析。综合以上分析表明：SWASH可以较好地模拟近岸复杂地形下的波流特性；数值模拟结果中流速随计算网格尺寸的变化敏感度较低，有效波高值随计算网格尺寸的变化表现得较为敏感，特别是当波浪发生破碎变形之后，其敏感程度较高；数值模拟结果中的流速和波高随计算时间步长的变化表现得并不敏感，其影响可以忽略不计。因此，采用SWASH模型模拟珊瑚礁水动力时，在高精度计算时间步长范围内，只需选取合适的计算网格尺寸便可以较好地模拟复杂地形下的波流传播特性。