不同坡度扭王字块体斜坡堤胸墙受力的数值模拟

孙大鹏，相才康*，邢晨曦，董 胜，刘 飞

(1.大连理工大学 海岸与近海工程国家重点实验室，大连 116024；2.中国海洋大学，青岛 266100；3.长春中海地产有限公司，长春 130000)

采用人工块体护面并设置堤顶胸墙是斜坡堤设计的通常结构型式，因胸墙波浪力事关结构的稳定性而成为诸多学者研究的热点课题。数值模拟试验因其有成本低、操作性强、不受比尺效应影响等优点而渐受青睐。GUANCHE[1]和LOSADA[2]为对COBRAS-UC模型进行验证，在物模试验的基础上对斜坡堤胸墙受力进行数值模拟，经过试验值的对比后，验证了该模型的有效性和准确性；王鑫钰[3]采用SWASH模型，通过等效底摩阻系数的方法，模拟了波浪在人工护面块体斜坡堤上的作用过程；张九山[4]通过在动量方程中添加阻力源项建立了多孔介质模型，基于物理模型试验和数值模拟，验证了在动量方程中添加多孔介质源项模拟护面块体的可行性；LU[5]考虑护面斜坡护面的消能影响，应用多孔介质模型进行模拟，建立了规则波与人工护面块体斜坡堤相互作用的数值模型；王鹏[6]采用多孔介质模型在FLUENT平台上模拟了块体护面防波堤与波浪的相互作用过程，得到了多孔阻力系数与多种异形块体糙渗系数的关系。上述学者在进行数值试验时，数值模拟中的特征参数(如多孔介质区的惯性阻力系数)通常借助专门的物模试验予以确定，使得此类数值模拟将依附于物模试验，数模成果只局限于物模试验的指定工况而不具备普适性。孙大鹏[7]与孙文豪[8]通过引入多孔介质模型，综合考虑多种因素对惯性阻力系数的影响，开展了扭王字块体带胸墙斜坡堤越浪量的数值模拟。

鉴于《港口与航道水文规范》[9]未明确给出扭王字护面块体斜坡堤胸墙波浪力的计算方法，刘飞[10]在引入多孔介质的基础上应用FLUENT对不规则波作用下扭王字块体斜坡堤胸墙水平波浪力开展了数值研究，以物理模型试验的胸墙最大水平波浪力为基准，先期得到相应试验工况惯性阻力系数C的率定值，进而综合考虑斜坡堤结构和水动力等多种因素对于惯性阻力系数C的影响，拟合得到C在坡度m=1.5情况下的计算公式，使得应用FLUENT软件对扭王字块斜坡堤胸墙受力的数值模拟独立于物模试验。但刘飞[10]研究成果亦仅适用于坡度m=1.5的扭王字护面块体斜坡堤胸墙波浪力的数值模拟，而坡度作为惯性阻力系数C的一个重要影响因素未在刘飞[10]C计算公式中予以体现，极大限制了该数值方法的应用范围。

本文基于刘飞[10]的数值构想，增加了坡度m=2.0、2.5情况下扭王字块斜坡堤胸墙水平波浪力的物模试验及数值研究，利用数值模拟率定得到相应试验工况的C值，经回归分析，并给出了不同坡度下惯性阻力系数C的计算公式。

1 数值水槽及其性能测试

1.1 控制方程

基本控制方程采用二维粘性流体的连续性方程和动量方程，湍流效应的模拟选用RNGk-ε模型，对流体自由表面的捕捉选用VOF方法。基本控制方程如下：

(1)

(2)

(3)

式中：ρ为流体密度；u为x方向的速度；w为z方向的速度；μ为动力粘性系数；p为压强；g为重力加速度；Fx和Fy为附加动量源项。

图1 数值波浪水槽示意图(单位：cm)Fig.1 Sketch of numerical wave sink

1.2 数值波浪水槽

选用王键[11]与唐蔚[12]基于FLUENT软件建立的消除造波端二次反射的主动吸收式二维不规则波浪数值水槽，数值水槽的结构如图1所示。水槽全长25 m、高0.8 m，左端为主动吸收式造波边界，消波区长度为6 m，设置在水槽右端。

1.3 数值水槽的性能测试

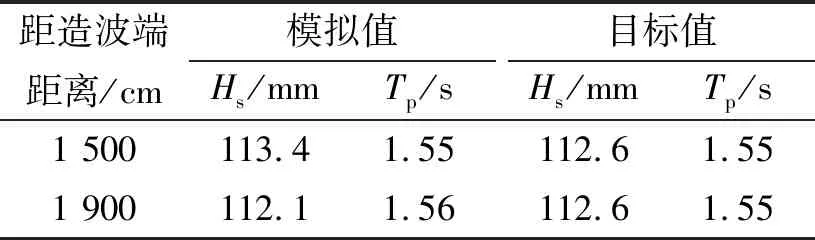
表1 数值水槽波浪特征要素对比Tab.1 Comparison of wave elements in numerical sink

不规则波浪谱采用JONSWAP谱(γ=3.3)，验证波况(本文的主要波况)：水深为d=45 cm，有效波高为Hs=112.6 mm，谱峰周期为Tp=1.55 s。模拟时长为180 s(确保波数大于100)，在距造波端x=1 500 cm和x=1 900 cm处设置检测线获取波面数据，而后处理得到模拟波谱与相应波浪特征要素，将模拟波浪谱与靶谱对比如图2，将波浪特征要素的目标值与模拟值对比如表1所示。

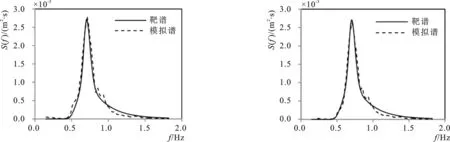
2-a 距造波端1 500 cm 2-b 距造波端1 900 cm图2 波浪的模拟谱与靶谱Fig.2 Simulated spectrum and target spectrum of wave

图3 模型断面示意图Fig.3 Schematic sketch of model section

2 惯性阻力系数的率定

2.1 工况组合

物模及数模试验(坡度m=2.0、2.5)采用的工况如表2所示共15种，模型断面结构如图3所示。在满足稳定要求的前提下，斜坡堤模型护面采用三种尺寸的扭王字块体(h=42 mm、60 mm、78 mm)铺设，块体尺寸如图4所示。共计进行试验90组次。

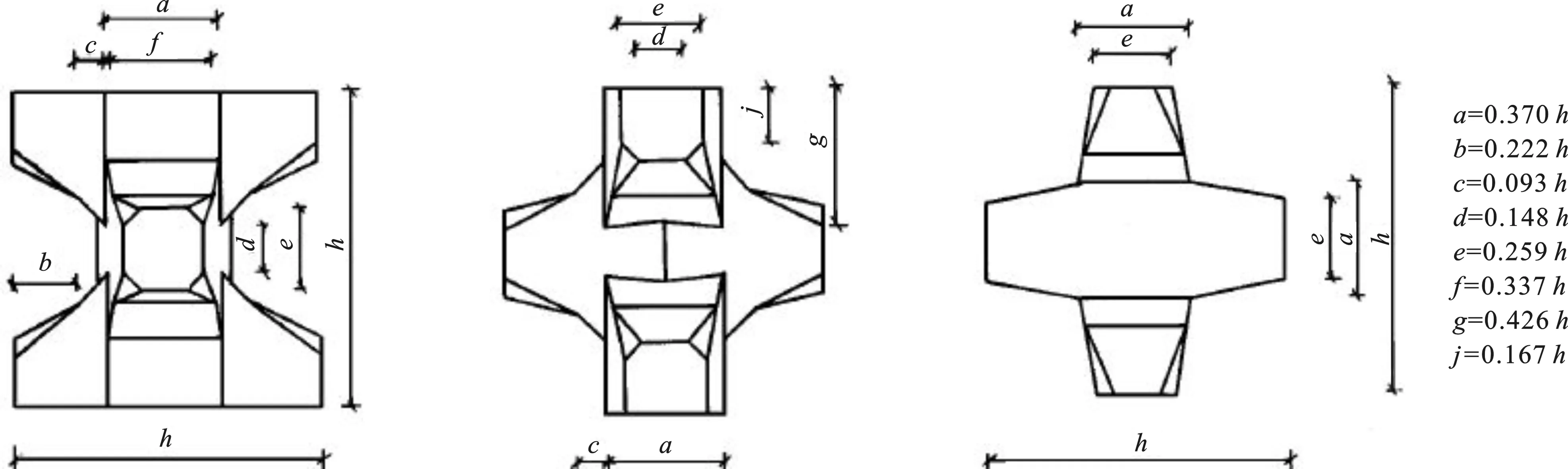
图4 护面块体示意图Fig.4 Sketch of armour blocks

表2 工况组合Tab.2 The combination of experimental conditions

2.2 多孔介质区

在数值模型中，多孔介质区设置为物理模型中的扭王字块体铺设区，利用多孔介质区惯性阻力源项的惯性阻力系数C来刻画扭王字块体铺设区的消波作用。其原理是在多孔介质区的动量方程中添加惯性阻力源项，忽略粘性阻力后，其表达式

(4)

式中：C为惯性阻力系数；v为流体的速度矢量；vi(i=1、2)分别为x、z方向的速度分量。

2.3 率定惯性阻力系数C的方法

以表2中试验序号为01，坡度m=2.0、块体尺寸h为42 mm的试验工况为例，对C值的率定过程进行介绍。第一步，设置C为5.0、2.0、1.0、0.5、0.1等值，分别进行数模计算，得到相对应的胸墙最大水平波浪力的数模计算值；第二步，绘制该实验工况下胸墙最大水平波浪力数模计算值与C值的变化趋势线，如图5(试验序号01)所示；第三步，利用该试验工况下的物模试验胸墙最大水平波浪力值从相应趋势线图5(试验序号01)上读出该工况的C率定值。按照上述方法获得了坡度m=2.0，块体尺寸h=42 mm时的15种试验工况C值率定结果如图5-a～5-o。

5-a 试验序号015-b 试验序号025-c 试验序号03

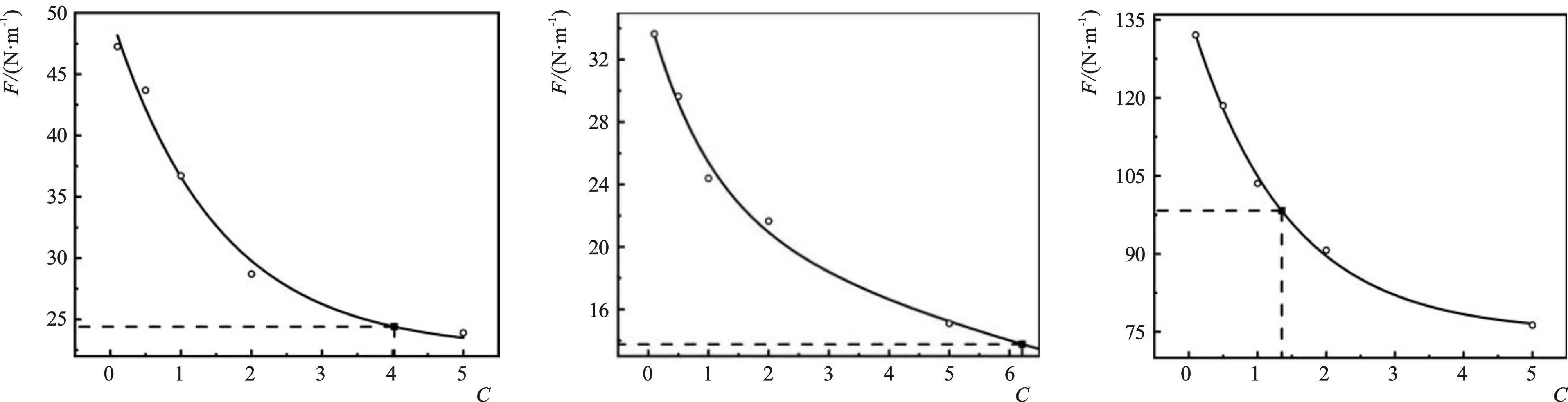
5-d 试验序号045-e 试验序号055-f 试验序号06

5-g 试验序号075-h 试验序号085-i 试验序号09

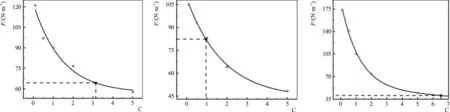
5-j 试验序号105-k 试验序号115-l 试验序号12

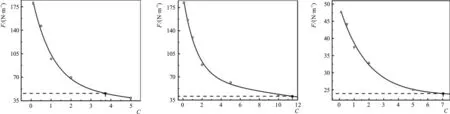
5-m 试验序号135-n 试验序号145-o 试验序号15图5 m=2.0、h=42 mm的C值趋势线Fig.5 Trend of C with m=2.0 and h=42 mm

坡度系数为m=2.0、2.5的扭王字块护面C值率定结果如表3和表4所示。

表3 惯性阻力系数率定值(m=2.0)Tab.3 Calibration value of inertia resistance coefficient (m=2.0)

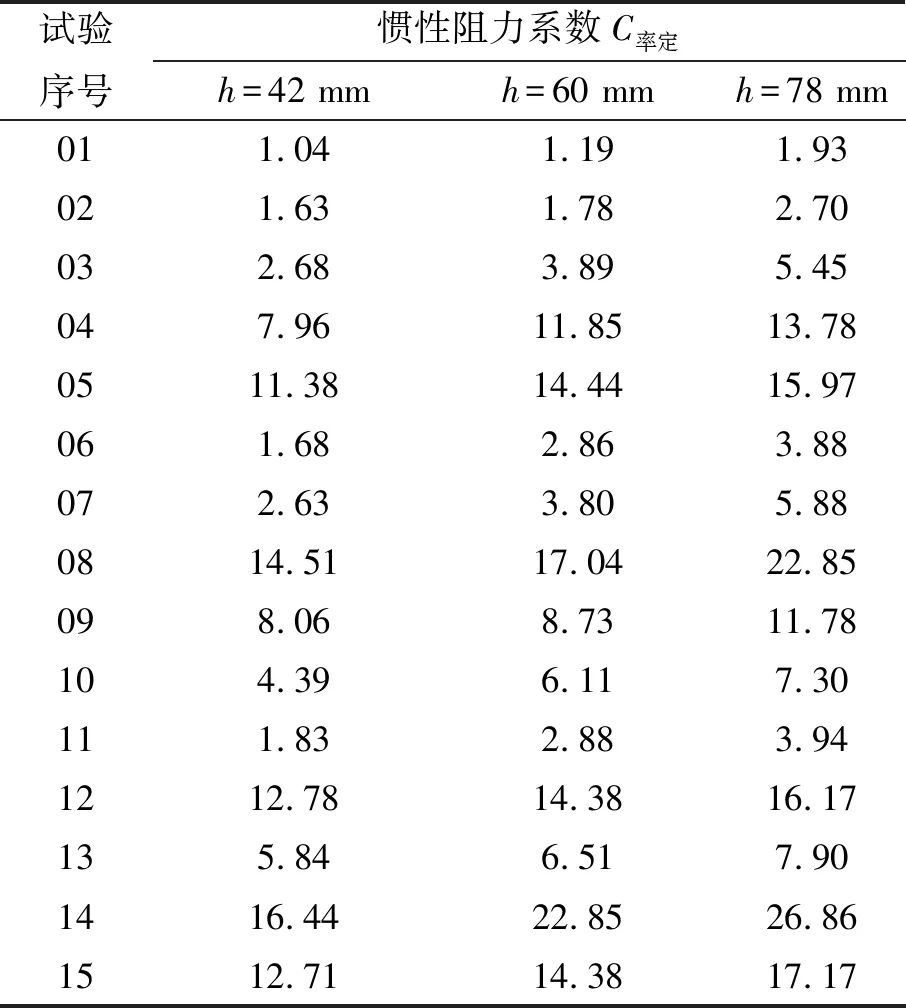
表4 惯性阻力系数率定值(m=2.5)Tab.4 Calibration value of inertia resistance coefficient (m=2.5)

取表3和表4的C率定值进行数值模拟得到的胸墙最大水平波浪力的计算值F数模，与相应工况下的物模值F物模进行比较如图6所示。由图可看出二者吻合程度较好，可知本文率定C率定值的方法可靠程度较高。

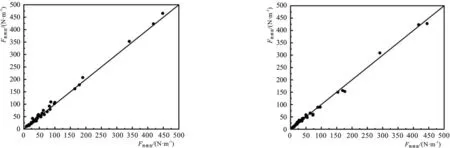
6-a m=2.06-b m=2.5图6 胸墙最大水平波浪力物模值与数模值对比图Fig.6 Comparison of measured and numerical values3 扭王字块体护面惯性阻力系数C的计算公式

基于本文的试验数据，发现坡度对惯性阻力系数C值的影响较大，且在进行单因素分析时不同坡度的C值与各影响因素间的函数形式有明显不同，为保证拟合精度，本文对坡度m=2.0或m=2.5单独分析并分别给出不同坡度C值的计算公式。

(5)

3.1 试验结果分析与C的计算公式拟合(m=2.0)

(1)Hs/L对C的影响。

固定其余因素数值，只变更Hs/L的数值，图7为C值的变化趋势。在图示区间内，C与Hs/L呈正相关性，选用线性形式函数进行拟合。

(2)d/Hs对C的影响。

固定其余因素数值，只变更d/Hs的数值，图8为C值的变化趋势。在图示区间内，C与d/Hs呈正相关性，选用线性形式函数进行拟合。

图7 Hs/L对C的影响Fig.7 Effect of Hs/L on C图8 d/Hs对C的影响Fig.8 Effect of d/Hs on C

(4)b1/Hs对C的影响。

固定其余因素数值，只变更b1/Hs的数值，图10为C值的变化趋势。在图示区间内，C与b1/Hs呈正相关性，选用指数形式函数进行拟合。

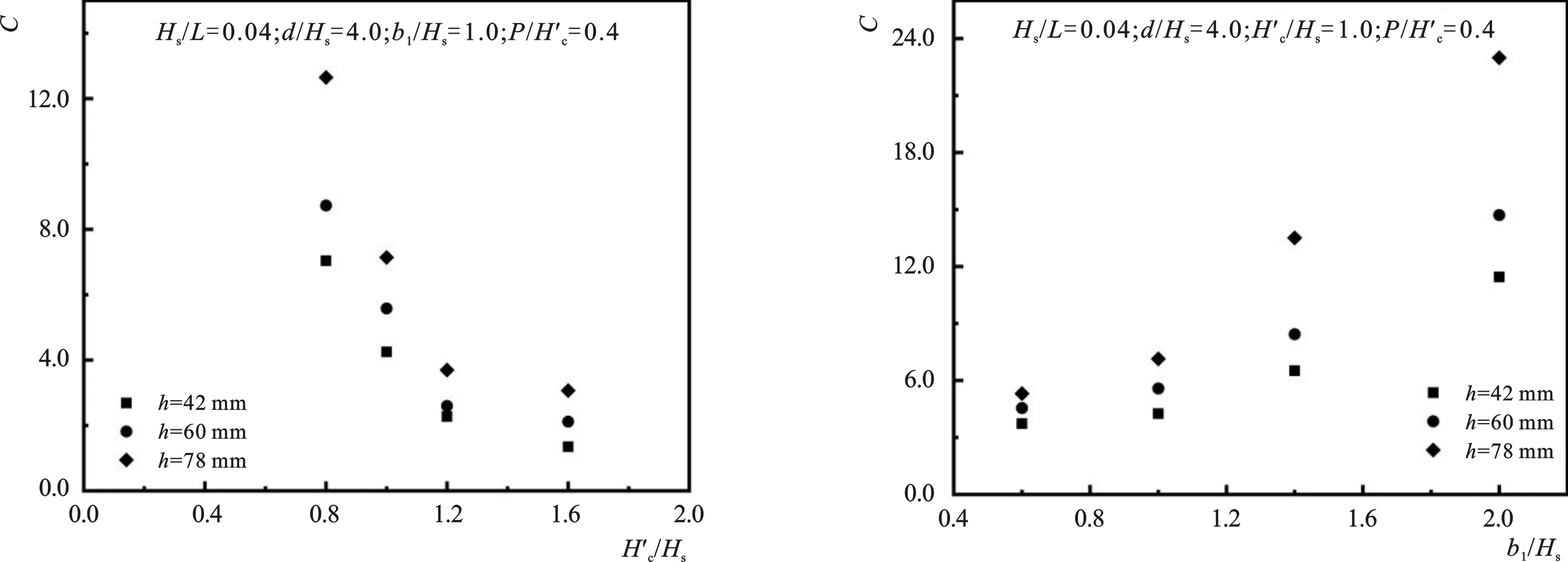
图9 H′c/Hs对C的影响Fig.9 Effect of Hc′/Hs on C图10 b1/Hs对C的影响Fig.10 Effect of b1/Hs on C

(6)h/Hs对C的影响。

固定其余因素数值，只变更h/Hs的数值，图12为C值的变化趋势。在图示区间内，C与h/Hs呈正相关性，选用指数形式函数进行拟合。

图11 P/H′c对C的影响Fig.11 Effect of P/H′c on C图12 h/Hs对C的影响Fig.12 Effect of h/Hs on C

(7)C的计算公式(坡度m=2.0)。

基于3.1(1)～(6)的分析，采用多元回归分析的方法，拟合出C在坡度m=2.0时的计算公式

(6)

3.2 试验结果分析与C的计算公式拟合(m=2.5)

(1)Hs/L对C的影响。

固定其余因素数值，只变更Hs/L的数值，图13为C值的变化趋势。在图示区间内，C与Hs/L呈正相关性，选用指数形式函数进行拟合。

(2)d/Hs对C的影响。

固定其余因素数值，只变更d/Hs的数值，图14为C值的变化趋势。在图示区间内，C与d/Hs呈正相关性，选用对数形式函数进行拟合。

图13 Hs/L对C的影响Fig.13 Effect of Hs/L on C图14 d/Hs对C的影响Fig.14 Effect of d/Hs on C

(4)b1/Hs对C的影响。

固定其余因素数值，只变更b1/Hs的数值，图16为C值的变化趋势。在图示区间内，C与b1/Hs呈正相关性，选用指数形式函数进行拟合。

图15 H′c/Hs对C的影响Fig.15 Effect of H′c/Hs on C图16 b1/Hs对C的影响Fig.16 Effect of b1/Hs on C

(6)h/Hs对C的影响。

固定其余因素数值，只变更h/Hs的数值，图18为C值的变化趋势。在图示区间内，C与h/Hs呈正相关性，选用线性形式函数进行拟合。

图17 P/H′c对C的影响Fig.17 Effect of P/H′c on C图18 h/Hs对C的影响Fig.18 Effect of h/Hs on C

(7)C的计算公式(坡度m=2.5)。

基于第3.2节式(1)～式(6)的分析，采用多元回归的方法，拟合出C在坡度m=2.5时的计算公式

(7)

3.3 惯性阻力系数计算公式的验证

(1)准确性验证。

将按计算式(6)、(7)计算得到的C计算值与表3、表4的C率定值进行对比如图19所示，C计算值与C率定值大致分布于直线y=x上，有较高的吻合度，表明按计算式(6)、(7)得出相应试验工况的C计算值结果准确性较高。

(2)有效性验证。

采用计算式(6)、(7)得到的C计算值进行数值模拟得出胸墙最大水平波浪力数模值F数模与相应的物模值F物模进行对比如图20所示，二者有较好的匹配度，说明应用计算式(6)、(7)对胸墙最大水平波浪力进行数值模拟可靠度较高。

19-a m=2.019-b m=2.5

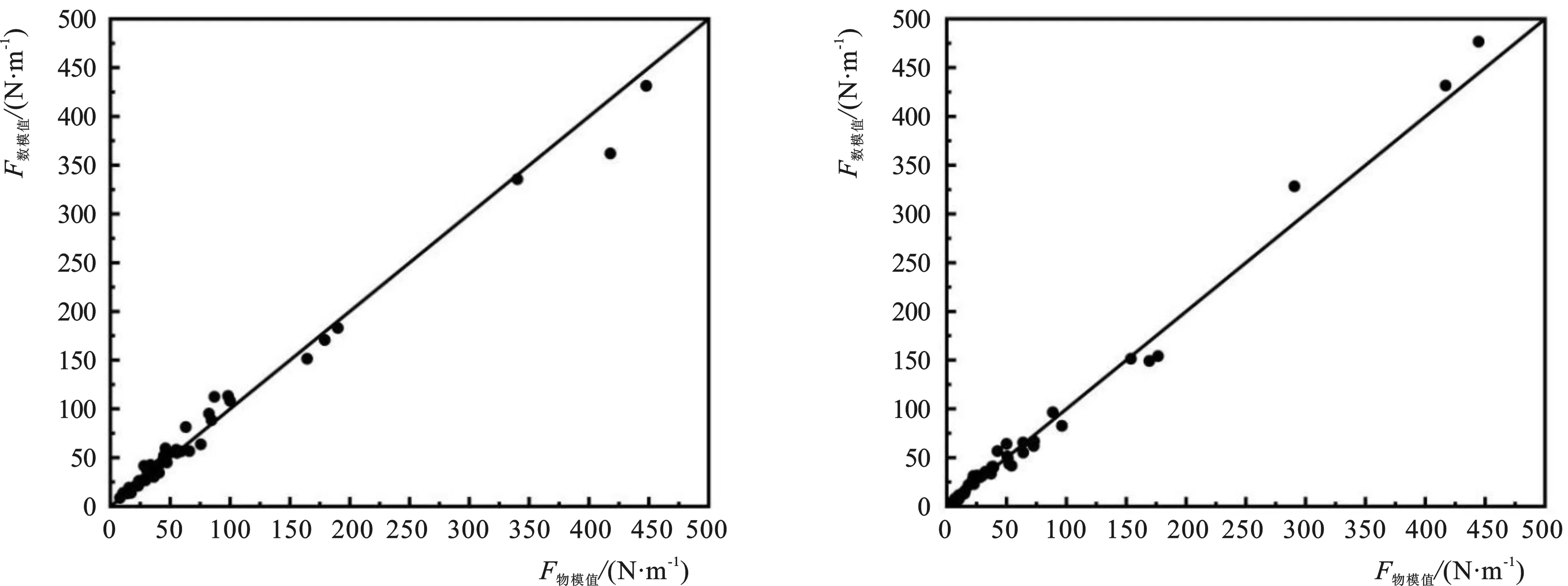
20-a m=2.020-b m=2.5图20 胸墙最大水平波浪力F的物模试验值和数模试验值对比Fig.20 Comparison between measured and numerical values of F

4 结论

(1)基于FLUENT软件开展了坡度m=2.0或m=2.5情况下的相关数值模拟研究，以物模试验的胸墙最大水平波浪力为基准，综合分析了相对块体尺寸、相对胸墙高度、相对堤顶超高、相对坡肩宽度、波陡、相对水深等因素对于惯性阻力系数C的影响，而后采用多元回归分析的方法，拟合了C在不同坡度下的计算公式，并对公式的有效性进行了验证。

(2)结合刘飞[10]的研究成果及本文研究，得到了惯性阻力系数在三个常用坡度(m=1.5或m=2.0或m=2.5)下的计算公式，使得通过引入多孔介质区模拟扭王字块斜坡堤胸墙水平波浪力的数值模拟成为一种独立的试验手段，为扭王字块体情况下斜坡堤胸墙水平波浪力的计算提供了一种新的方法，并对相关的工程设计具有一定的参考价值。