例说平方根与算术平方根
2022-02-03 11:23:00李中清
初中生世界 2022年46期
文/李中清
通过平方根的学习,我们知道,如果x2=a(a≥0),那么x叫作a的平方根,也称为二次方根。正数a的正的平方根记为,负的平方根记为;0 的平方根为0;负数没有平方根。其中,正数a的正的平方根也称为a的算术平方根,0 的算术平方根为0。下面,我们通过几道例题加深对平方根与算术平方根的理解。
例1已知一个正数a的两个平方根分别是x+3和2x-15,求x和a的值。
【分析】根据正数的平方根互为相反数列方程求解即可。
解:由题意得x+3=-(2x-15),
解得x=4。
∴a=(4+3)2=49。
故x的值为4,a的值为49。
例2求式中的x的值:(x+3)2=16。
【分析】根据平方根的定义解方程即可。
解:(x+3)2=16,
解得x=-7或x=1。
例3化简=( )。
A.±2 B.-2
C.4 D.2
【分析】根据算术平方根的意义计算即可。
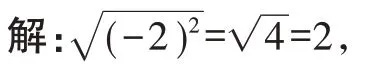
故选D。
例4若实数m、n满足|m-n-5|+=0,则3m+n=______。
【分析】根据非负数的性质求出m和n的值,再代入3m+n计算即可。

∴m-n-5=0,2m+n-4=0,
解得m=3,n=-2。
∴3m+n=9-2=7。
故答案为7。
【分析】根据非负数的性质求出x,进而求出y,再根据平方根的概念解答即可。
解:由题意得x-4≥0,4-x≥0,则
x≥4,x≤4,即x=4。
∴y=7。
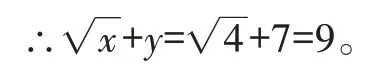
∵9的平方根是±3,

猜你喜欢
中学生数理化·七年级数学人教版(2022年3期)2022-03-16 05:55:42
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:15
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:15
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:50
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:50
小天使·二年级语数英综合(2017年9期)2017-10-20 21:09:35
广东教育·高中(2017年9期)2017-09-27 20:09:10
中学生数理化·七年级数学人教版(2017年11期)2017-04-18 12:13:43
小雪花·小学生快乐作文(2016年12期)2017-03-08 00:50:58
小天使·一年级语数英综合(2016年5期)2016-05-14 23:32:12

