基于不同分段方式和速度类型的赛艇配速策略研究

易 清 ，吴 添，刘鸿优，黎涌明*

在高水平赛艇比赛中，奖牌的争夺只在不到1 s之间，任何有助于获得1%优势的策略对于力争在比赛中实现突破的运动员来说都值得尝试（资薇 等， 2013）。运动员在比赛中的做功或能量消耗的分配被称为配速策略（Abbiss et al.， 2008）。研究发现，不同运动水平的运动员所采用的配速策略不同（Konings et al.， 2016），采用不同的配速策略可以给运动员竞技表现带来显著改变（Hettinga et al.， 2011）。

赛艇项目要求运动员以最短的时间完成2 000 m的比赛距离，在5～8 min的比赛中，运动员既需要避免冲过终点时还有能量节余，也需要避免过早出现疲劳而后程出现明显降速（黎涌明， 2013；黎涌明 等， 2017）。Kleshnev等（2001）对悉尼奥运会上赛艇项目的配速策略进行研究指出，4个比赛分段（4×500 m）相对于全程平均速度的百分比分别为+2.8%、-1.2%、-1.3%和-0.1%。有研究采用此方法围绕赛艇项目的不同运动形式（水上划vs测功仪）（Garland， 2005）、比赛轮次（决赛 vs 非决赛）（Muehlbauer et al.， 2011）、艇种（Kleshnev et al.， 2001），以及运动员的运动水平（Brown et al.， 2010）、性别（Muehlbauer et al.，2010）、国家（Kleshnev et al.， 2001）进行了配速策略的探究。然而研究结果显示，不同比赛轮次、艇种、运动水平和性别之间均不存在显著差异，这很大程度上降低了配速策略在赛艇项目中的重要性。导致这一局面的原因可能与研究所采用的分段方式（4×500 m）和速度类型（相对速度）有关。

国际赛艇比赛竞争日趋激烈，运动员在2 000 m中任何一个细小赛段（如起航和冲刺）的表现对最终比赛名次都可能有决定性影响（陈小平 等，2011；韩炜 等，2013）。然而，将2 000 m距离粗略分为4段可能会掩盖诸多关键赛段的信息。Foster等（1994）建议在进行配速策略研究时采用比赛全程的5%～10%的距离来进行分段，而5%～10%的分段在赛艇比赛中对应为100～200 m，但国际赛艇联合会（Fédération Internationale des Sociétés d’Aviron，FISA）官方网站对于2010年以前的比赛只提供500 m分段的数据，使得这一分段方式难以实现。自2010年起，FISA提供的比赛数据细化到每50 m分段，这为采用更细分段对赛艇配速策略进行研究提供了可能。然而，已发表的文献中鲜见有关赛艇项目不同分段方式的比较研究。

传统配速策略研究选用的速度类型大多为相对速度，即各分段速度占全程平均速度的百分比。对相对速度数据进行分析能够将同一运动项目在不同时空（如不同场次、比赛地点）下的比赛数据进行比较，也可以对不同运动项目的配速策略进行比较。对于受气象条件影响较大的运动项目（如赛艇项目），采用相对速度还能最大程度消除不同场次气象条件（如风速）对速度的影响。然而，在赛艇项目中，采用相对速度得到的结论似乎不足以区分不同水平的运动员（Brown et al.，2010）。在这种情况下，试图通过比较不同水平运动员的配速策略为运动员参赛提供指导就难以实现。事实上，赛艇比赛成绩是完成相同距离的时间，最先冲过终点的艇对应的绝对速度更快。因此，绝对速度数据能够保留不同艇的名次或运动水平信息。此外，以往针对不同运动水平运动员的配速策略研究大都涵盖了一个较大的能力范围，如Brown等（2010）和 Garland（2005）分别以第 1～23名和第 1～170名参赛队伍为研究对象对奥运会、世锦赛和英国室内锦标赛赛艇数据进行了分析。尽管上述研究能够为运动员长期发展提供参考，但对于具备进入决赛A组能力的前6名运动员（或参赛队伍）而言，配速策略研究针对一个更小的能力范围才能为其争金夺牌提供有价值的建议。

由于历届奥运会赛艇比赛只提供每500 m分段的比赛数据，未进行更为细致的赛段划分，本研究选取2010—2019年世界赛艇锦标赛（以下简称“赛艇世锦赛”）决赛A组（第1～6名）参赛队伍的比赛数据，基于不同分段方式（500、200、50 m）以及不同速度类型（绝对速度、相对速度）对高水平赛艇比赛中不同运动水平队伍（第1名、第2～3名、第4～6名）的配速策略进行比较。提出以下假设：1）相比于500 m分段，200、50 m的分段方式能够提供更为详细的配速策略信息，不同运动水平队伍之间的差异在更精细的分段方式中体现得更为具体；2）不同运动水平队伍在不同的速度类型中呈现出的差异不同，将两者结合能够发现不同运动水平队伍的更多配速特征。

1 研究对象与方法

1.1 研究对象

以2010—2019年赛艇世锦赛6个艇种（W1x、W2-、W2x、M2x、W4x和M4x）决赛A组所有参赛队伍的配速策略为研究对象，数据样本包括各参赛队伍每50 m比赛平均速度数据。剔除出现以下任意情况的比赛数据：1）弃赛或比赛被判犯规的艇；2）最终比赛成绩或50 m分段成绩中任意一个比赛分段的数据为0、异常值或者缺失值的艇。最终有266条艇的比赛分段数据被纳入分析。数据来源于FISA官方网站，实时比赛数据由Omega Timing获得授权采集。

1.2 数据处理

1）基于各艇每50 m平均绝对速度，换算出各艇每500、200 m的平均绝对速度。2）为了比较基于绝对速度和相对速度的配速策略研究结果的差异，对每500、200、50 m分段的绝对速度数据进行标准化转换，计算出每500、200、50 m分段的相对速度。计算方式为：各艇的分段绝对速度除以该艇全程平均绝对速度。3）根据比赛排名，将决赛A组的参赛队伍分为3个实力水平（水平1：第1名；水平2：第2～3名；水平3：第4～6名），比较3个水平队伍在配速策略上的差异。

1.3 统计分析

本研究采用数据级数推断的非临床推断方法对3个水平的队伍的绝对速度和相对速度在各比赛分段的差异进行统计学推断。均值差异被转换成标准化效应值（ef‐fect size，ES），推断结果以效应值±90%置信区间的形式呈现，并根据如下标准对ES的大小进行划分：ES＜0.2，微小无意义差异；0.2＜ES＜0.6，小程度差异；0.6＜ES＜1.2，中等程度差异；1.2＜ES＜2.0，大程度差异；ES＞2.0，非常大程度差异（刘鸿优 等，2017； Batterham et al.， 2006； Hop‐kins et al.， 2009）。ES=±0.2被确定为最小显著意义阈值，当效应值的90%置信区间未同时包含-0.2和0.2时，该差异值则被确定为是清晰的。同时，差异值为清晰的正值、负值或微小无意义值的可能性按如下标准进行界定：可能性＜0.5%，极其不可能；0.5%＜可能性＜5.0%，非常不可能；5.0%＜可能性＜25.0%，很不可能；25.0%＜可能性＜75.0%，可能；75.0%＜可能性＜95.0%，很可能；95.0%＜可能性＜99.5%，非常可能；可能性＞99.5%，极其可能（刘鸿优 等，2017； Hopkins et al.， 2009）。

2 研究结果

基于3种分段方式得到的3个水平队伍在各个比赛分段中的绝对速度（图1a～1c），不论何种分段方式，水平1和2间均无显著差异，水平1和3在中程和后程差异显著（ES： -0.31±0.29～-0.20±0.29；可能性：可能），水平2和3在后程差异显著（ES： -0.30±0.23；可能性：可能～很可能；图2）。具体来看，500 m分段时，水平1和3在500～2 000 m间差异显著（ES：-0.24±0.29～-0.20±0.28；可能性：可能），水平2和3在1 500～2 000 m间差异显著（ES：-0.26±0.23；可能性：可能）；200 m分段时，水平1和3在800～2 000 m间差异显著（ES：-0.25±0.29～-0.20±0.29；可能性：可能），水平2和3在1 400～2 000 m间差异显著（ES： -0.27±0.23～-0.21±0.23；可能性：可能）；50 m分段时，水平 1和 3在 200～250 m、500～550 m、650～700 m、800～850 m、950～1 950 m间差异显著（ES：-0.31±0.29～-0.20±0.29；可能性：可能），水平2和3在 1 150～1 200 m、1 450～2 000 m 间差异显著（ES：-0.30±0.23～-0.21±0.23；可能性：可能～很可能）。

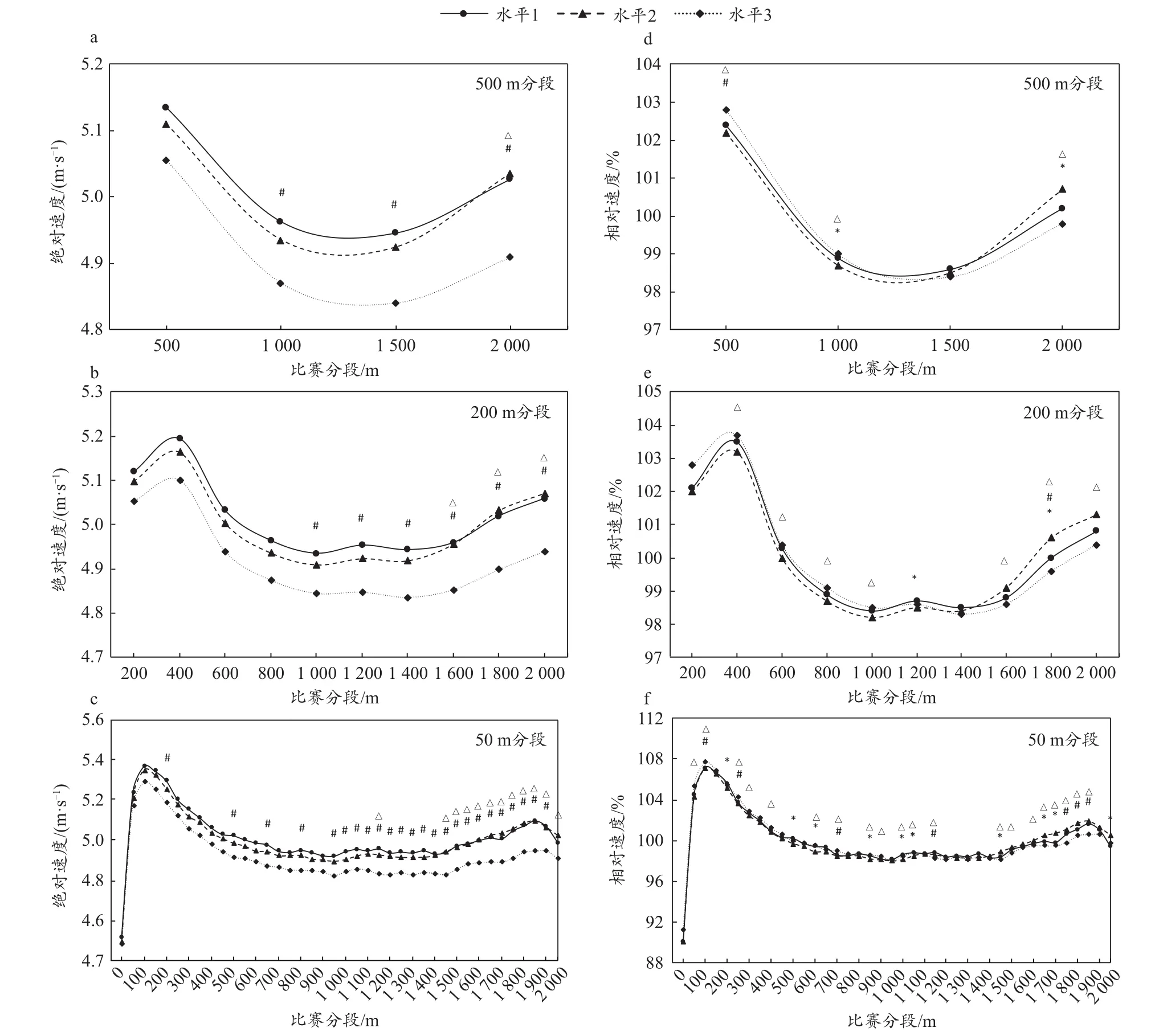
图1 3种分段方式中3个水平队伍的绝对速度和相对速度在各比赛分段的比较Figure 1. Comparisons of Absolute and Relative Speed of Three Levels of Teams in Each Racing Stage under Different Splitting Methods

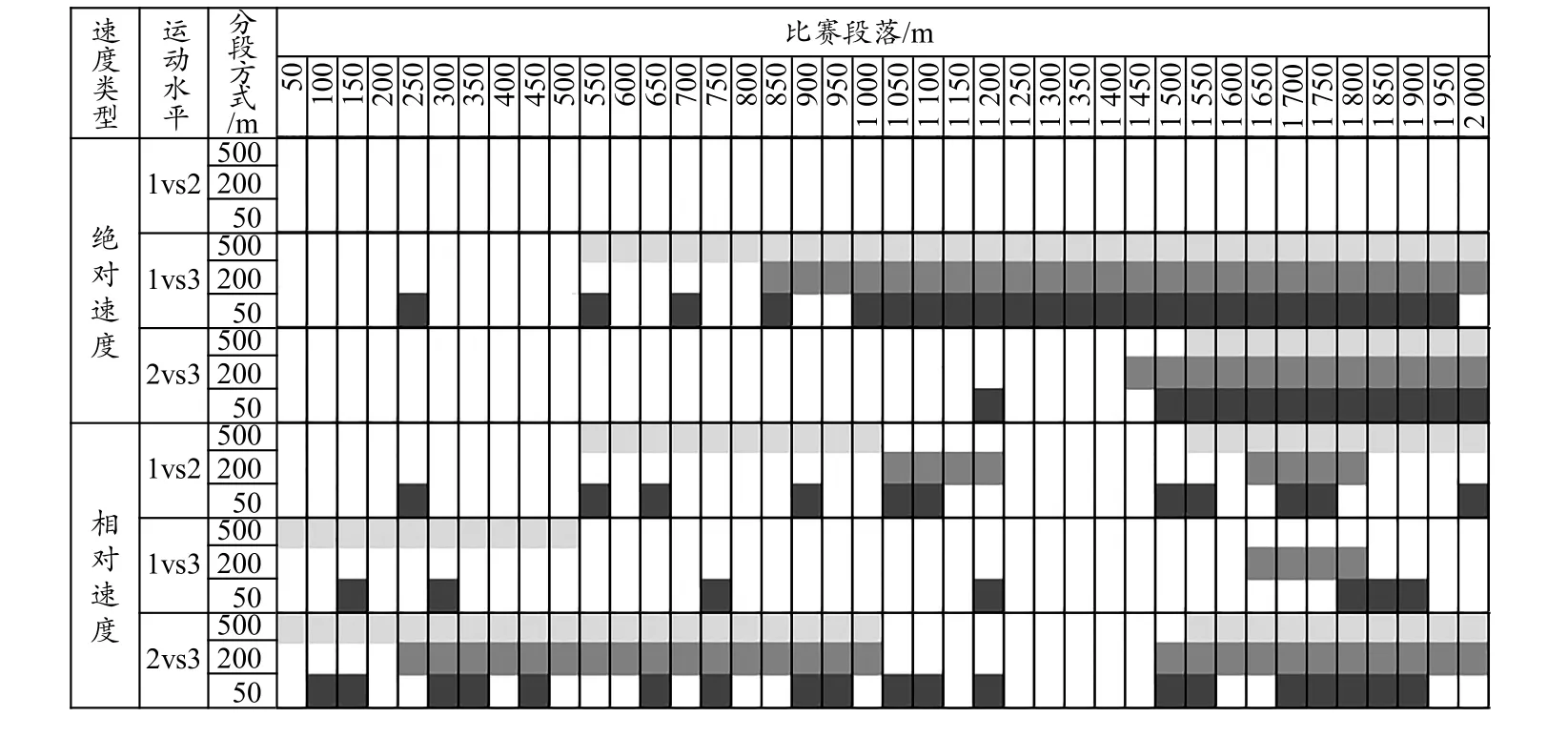
图2 3个运动水平队伍之间的绝对速度、相对速度差异Figure 2. Differences in Absolute and Relative Speed between Three Levels of Teams

基于3种分段方式得到的3个水平队伍在各个比赛分段中的相对速度（图1d～1f），不论何种分段方式，水平1、2和3两两间在部分分段差异显著（图2）。3个水平间在不同分段方式中呈现出的差异不同，500 m分段时，水平1和2在500～1 000 m、1 500～2 000 m间差异显著（ES： -0.22±0.30～0.25±0.30；可能性：可能），水平1和3在0～500 m间差异显著（ES： 0.23±0.27；可能性：可能），水平2和3在0～1 000 m、1 500～2 000 m间差异显著（ES： -0.43±0.23～0.28±0.22；可能性：可能～非常可能）；200 m分段时，水平1和2在1 000～1 200 m、1 600～1 800 m间差异显著（ES： -0.21±0.30～0.31±0.30；可能性：可能），水平1和3在1 600～1 800 m间差异显著（ES： -0.22±0.28；可能性：可能），水平2和3在200～1 000 m、1 400～2 000 m间差异显著（ES：-0.50±0.23～0.21±0.22；可能性：可能～非常可能）；50 m分段时，水平1和2在200～250 m、500～550 m、600～650 m、850～900 m、1 000～1 100 m、1 450～1 550 m、1 650～1 750 m、1 950～2 000 m 间 差 异 显 著（ES： -0.32±0.30～0.38±0.30；可能性：可能～很可能），水平1和3在100～150 m、250～300 m、700～750 m、1 150～1 200 m、1 750～1 900 m间差异显著（ES： -0.34±0.30～0.25±0.28；可能性：可能～很可能），水平 2和3在 50～150 m、250～350 m、400～450 m、600～650 m、700～750 m、850～950 m、1 000～1 100 m、1 150～1 200 m、1 450～1 550 m、1 650～1 900 m 间差异显著（ES： -0.51±0.23～0.30±0.23；可能性：可能～非常可能）。

3 分析与讨论

研究结果表明，分段方式和速度类型能够影响不同运动水平队伍配速策略比较的结果。研究结果支持研究假设，即更细的分段能够提供更为详细的配速策略信息，基于绝对速度的配速策略能够更为直观地展现不同运动水平间的差异。

3.1 不同分段方式对基于绝对速度的配速策略分析的影响

绝对速度直观反映了3个运动水平配速策略的差异，不同分段方式对绝对速度下3个运动水平的配速策略分析的影响较小。不管差异是否显著，水平1和2各分段的速度均快于水平3；水平1在前75%赛段的速度快于水平2，在后25%赛段与水平2几乎相同。对3个水平绝对速度在各分段差异的统计学推断表明，水平1和2在各分段的差异均不显著，这反映了赛艇世锦赛中竞争的激烈程度；水平1和3在比赛中程和后程的分段差异显著，水平2和3在比赛后程的分段差异显著，这反映决赛A组中低水平与高水平队伍的主要差异不在比赛的前程（前25%），而在中程和/或后程，这与对赛艇模拟比赛能量代谢动态过程的研究发现一致（吴昊 等， 2004）。Mader（1977）和Nolte（2005）通过能量代谢过程的测试和计算机模拟发现，在6.0～7.0 min的模拟比赛中，无氧供能主要发生在比赛开始的前1.5 min（前500 m），而之后的能量供应方式主要为有氧供能。有氧供能能力的差异可能是水平3在中程和/或后程速度显著较低的主要原因（资薇， 2015）。低运动水平队伍在后程的绝对速度与高水平队伍差异更大或更明显，这与中/长跑（Hettinga et al.， 2019）、短道速滑（Konings et al.， 2016）、速度滑冰（李博 等，2020）、游泳（Robertson et al.， 2009） 和自行车（Abbiss et al.， 2013）等项目的相关研究结果类似。

尽管不同分段方式带来的影响较小，但更小的分段提供了不同运动水平绝对速度差异更详细的信息。1）水平1和3，以及水平2和3之间存在显著差异的分段分布于比赛的中程和/或后程。但当分段方式细化至50 m时，原来未出现显著差异的赛段中的个别分段出现了显著差异。如，在500、200 m分段方式中（图1a、1b），水平1和3的绝对速度在比赛开始阶段无显著差异，但在50 m的分段方式中（图1c），水平1和3在200～250 m分段出现了显著差异。这说明随着分段方式的不断细化，其所提供的信息变得更加丰富，更多细小分段的差异能够显现出来。2）更加精细的分段方式所能提供的比赛细节信息还体现在更加精确地确定差异显著的分段所在的位置。在3种分段方式中，水平1和3的绝对速度在比赛中程和后程均出现了显著差异，但500 m分段方式对应的中程是500～1 000 m，而200、50 m的分段方式对应的中程能够进一步细化为800～1 000 m和950～1 000 m。对于参加赛艇世锦赛的队伍来说，能够将某一关键分段由500～1 000 m细化为950～1 000 m有助于更为精细地调控自身的配速策略。3）在200 m和50 m的分段方式中，3个水平队伍在出发之后经过100～150 m这一比赛分段，其绝对速度和相对速度开始出现下降趋势。且在比赛冲刺阶段，3个水平在1 800～1 900 m这一比赛区间段均出现了减速趋势。这也表明了更加精细的分段方式能够为不同水平队伍在比赛出发和冲刺阶段的速度结构的调整提供更加准确的参考。

3.2 不同分段方式对基于相对速度的配速策略分析的影响

不同分段方式对相对速度下3个运动水平配速策略分析的影响较大，3个运动水平之间出现显著差异的分段随分段方式的不同而不同。水平1和2的相对速度在某些分段出现显著差异，但这种差异在500 m分段方式中对应500～1 000 m和1 500～2 000 m这2个分段，在200 m分段方式中对应1 000～1 200 m和1 600～1 800 m，在50 m分段方式中对应200～250 m、500～550 m、600～650 m、850～900 m、1 000～1 100 m、1 450～1 550 m、1 650～1 750 m、1 950～2 000 m。这些由不同分段方式得到的有显著差异的分段既存在共性也存在区别。500、200 m分段方式由于是多个50 m的平均速度（即10×50 m和4×50 m），可能会掩盖个别50 m分段的差异（即在更小的分段方式中差异显著，但在更大的分段方式中差异不显著），或者将多个50 m分段的差异叠加迁移至其他50 m分段（即在更小的分段方式中差异不显著，但在更大的分段方式中差异显著）。这种掩盖或迁移可能导致运动员和教练员对一些关键赛段的错误判定。同样的情况也存在于水平1和3，以及水平2和3的比较当中。

尽管3个运动水平之间出现显著差异的分段随分段方式的不同而不同，但3种分段方式得到的配速策略都为抛物线型，与前人研究结果一致（Garland， 2005； Muehl‐bauer et al.， 2010）。此外，忽略差异显著与否，3个水平的相对速度在不同的比赛阶段有着不同的差异，且未受到分段方式的影响。水平2和3的差异最大，水平1的相对速度在绝大部分比赛分段中都介于水平2与3之间。水平2在前半程有着最低的相对速度，但是其在后半程则比水平1和3更高。水平3则出现了与其相反的特征，其在前半程高于水平1与2，但是其在后半程则显著落后于水平1和2。水平1在比赛中采取了相对更加均匀的配速策略，这也可能是其最后获胜的重要因素之一。水平2在前半程相对更加保守，从而使得其在后程有着更好的冲刺速度，但可能由于在前半程落后于水平1太多，后程全力加速也无法弥补差距。而水平3在前半程采用过于激进的策略，导致后程体能储备不足而失去竞争奖牌的机会。这一结果表明，当前世界高水平赛艇比赛中水平更高的队伍的配速策略出现了向均匀型发展的趋势，更加均匀的配速策略更有可能带来比赛成绩提升，这与Nolte（2011）的研究结论一致。

3.3 不同速度类型对不同运动水平队伍配速策略分析的影响

配速策略是指比赛过程中体力或能量的分配，其选用的指标主要为速度和功率（Thompson， 2014）。一些功率方便测量的运动项目（如自行车）往往采用功率指标（Granier et al.， 2018），而对于功率不易测量的运动项目（如跑步），或比赛中不允许采用设备进行功率测量的运动项目（如赛艇），速度是研究配速策略的替代指标（裘艺 等，2002）。现有赛艇配速策略的研究大都从FISA官网获取比赛的时间数据，并进一步将其转化为绝对速度（Nolte， 2011）和相对速度（Garland， 2005）。绝对速度能够直观反映运动员的水平，但相对速度有助于比较不同运动水平（Brown et al.，2010）或不同运动子项（Muehlbauer et al.， 2011）的配速策略。大部分研究对应的受试者运动水平跨度较大，或涉及了不同艇种的比较，因此主要采用的速度类型为相对速度（Garland， 2005； Muehlbauer et al.， 2010，2011）。

尽管采用相对速度数据进行分析实现了不同运动水平或艇种的比较，但基于这种速度类型得到的配速策略信息可能与基于绝对速度得到的信息存在较大差异。1）在基于相对速度的分析中，水平1和2在部分分段差异显著，而在基于绝对速度的分析中，二者在所有分段中的差异均不显著。2）在基于绝对速度的分析中，不同分段方式得到的有显著差异的分段较为类似，但基于相对速度的分析中，不同分段方式得到的有显著差异的分段区别较大。3）在基于绝对速度的分析中，水平1和3之间存在显著差异的分段数量最多，水平2和3之间其次，水平1和2之间最少；但在基于相对速度的分析中，水平2和3之间存在显著差异的分段数量最多，水平1和2之间其次，水平1和3之间最少。4）基于不同速度类型进行不同水平的比较时，有显著差异的分段所在的赛程位置不同。例如，基于绝对速度的分析中，水平2和3之间存在显著差异的分段主要在后程（最后25%），但是基于相对速度的分析中，这2个运动水平存在显著差异的分段存在于前半程（前50%）和后程（最后25%）。

3.4 研究的局限性

1）由于比赛是连续不间断进行的，相邻分段之间的速度会存在较大关联性，而传统的统计方法很难解决这种非独立数据对最终分析结果造成的影响。未来的研究可在充分考虑相关影响变量的基础上建立数学模型，从而减少甚至控制其对配速表现分析结果的影响。

2）尽管本研究采用了数据级数推断法分析3个水平在各分段差异的显著性，但是仍未发现水平1和2在绝对速度的统计学差异，但在实际比赛中，获得金牌的艇与其他艇之间存在着一定差异，因此研究结果对于具备夺得奖牌实力的运动员冲击金牌的参考价值有限。

3）由于本研究是将所有比赛项目的数据合并进行的整体分析，未来通过对各艇种进行单独分析，可能会发现更多具有实际参考价值的信息。

4 结论

1）更加精细的分段方式能够提供更多信息来探析比赛的动态发展过程。相比于传统的500 m分段方式，200、50 m的分段方式能够提供更多有价值的配速结构信息。未来随着赛艇比赛中数据采集系统的不断升级，更加复杂的比赛数据将有利于研究人员建立更加科学的配速策略分析模型。

2）绝对速度能够更为真实地反映不同运动水平的艇的实力差异。未来可考虑纳入更多生物力学和生理学指标进行分析，进一步探究赛艇运动员配速策略属于主动战术选择还是生理学结果。