基于开源软件的无人机飞行仿真

鹿珂珂， 刘登攀， 王超

(海军航空大学航空作战勤务学院， 烟台 264001)

无人机(unmanned aerial vehicle，UAV)飞行控制的算法设计和验证是无人机研制的关键环节[1]，无人机外回路的飞行控制算法应用较为广泛的是经典控制算法，如比例-积分-微分(proportion-integration-differentiation，PID)[2]，但是该算法的参数一般固定不变，在变量多、非线性的情况下控制效果不佳。目前，还存在很多非线性控制方法，这些方法可以很好地实现无人机的飞行控制并且自适应速率较小[3]，比如文献[4]针对无人机滚转控制提出了非线性L1控制算法，但是并没有对其纵向控制算法进行设计，仅仅采用了MATLAB对算法本身进行了仿真验证。文献[5]和文献[6]中提出了实现油门和升降舵控制解耦的总能量控制(total energy control system，TECS)算法，并在纵向通道分别对飞机和导弹的高度与速度进行了解耦控制。文献[7]则在对固定翼无人机数学模型进行分析基础上，基于MATLAB对纵向飞行控制律进行了设计仿真。文献[5]和文献[7]未提及横侧向通道的算法设计，文献[6]在横侧向通道上则采取了比例式控制律，相关仿真验证均为基于MATLAB对算法性能的验证。文献[8]指出，飞行仿真可以对无人机的稳定性和可操作性、飞行控制系统性能进行检验并改进，降低在实际飞行中的操作风险，并对无人机全系统进行了仿真和测试，但系统设计基于商业研发用途，难以复现，并且不包含实时的视景展示。文献[9]针对无人机的飞行控制仿真采用了硬件在环仿真的形式，将无人机真实的控制器与无人机机体等虚拟部分联合组成的仿真系统，但这种仿真方式如果没有加上真实的转台进行测试，与软件在环仿真[10]没有很大的区别，即完全用计算机就可以模拟出无人机飞行时的状态。基于上述研究，现针对无人机的飞行控制算法设计和仿真问题，研究无人机横侧向L1控制和纵向总能量控制算法的集成与具体实现，并基于开源软件，采用软件在环仿真的方式开发无人机的飞行仿真系统，用于验证所设计无人机飞行控制算法性能，并且可以通过视景仿真进行直观显示和分析。

1 无人机轨迹控制算法

1.1 L1算法

L1算法是指在无人机期望路径上选取一个参考点，根据这个参考点和无人机当前水平速度计算出水平期望加速度的算法。而L1指的就是期望路径上的参考点与无人机当前水平位置的距离，定义η为速度V与L1之间的夹角。如图1所示，根据这个参考点和当前水平速度可以计算出水平期望加速度，公式为

图1 L1算法示意图Fig.1 L1 algorithm diagram

(1)

无人机在当前时刻的期望运动是一个半径为R、速度为V的圆周运动。所以在航向控制上也应该给一个相应的期望偏航角速率前馈，表达式为

(2)

如图2所示，当无人机跟踪直线时的期望加速度为

η1为目标路径与L1之间的夹角；η2为速度V与目标路径之间的夹角图2 无人机跟踪一条直线示意图Fig.2 Schematic diagram of UAV tracking a straight line

(3)

如图3所示，当无人机跟踪圆弧时的期望加速度为

Ψ为速度V的航向角；θ为无人机的方位角；η3为无人机位置和圆弧路径中心连线与圆弧路径交点处的弦切角图3 无人机跟踪一条圆弧的路径示意图Fig.3 Path diagram of UAV tracking an arc

(4)

跟传统基于侧偏距的比例-微分(proportion-differentiation，PD)算法相比，L1算法中会根据V的速度不同，计算出的期望加速度也不同，这对于实际飞行时不同的期望飞行速度以及环境风的干扰都有很好的适应能力。

算法在具体实现时，需要改动和调校两个数值，一个是该系统的周期L1-P，另一个是该系统的阻尼比L1-D，两者满足关系式L1=L1-PL1-DV/π 。阻尼比参数L1-D一般设置在0.65～0.8，周期参数L1-P用来调试系统的自然频率。根据式(3)所示二阶系统，可以计算得到自然频率为

(5)

可见，不同的周期参数下系统会有不同的自然频率，从而得到不同的跟踪效果。

1.2 总能量控制(TECS)

TECS是运用能量控制与分配的方法，将速度控制与高度控制(切向加速度与纵向航迹角)进行解耦，用油门来控制总能量，用升降舵(俯仰角)来控制动能和势能之间的能量转换。

如图4所示，无人机纵向上的运动方程为

图4 飞机纵向受力示意图Fig.4 Schematic diagram of aircraft longitudinal force

(6)

式(6)中：x为水平距离；H为高度；T和D分别为推力和阻力；γ为航迹倾角；m为无人机质量；g为

重力加速度；V为无人机速度。

航迹角较小时，有sinγ≈γ，得

(7)

无人机质点总能量方程表示为

(8)

式(8)中：ED和ES分别为无人机的动能和势能。单位总能量为

(9)

对式(9)微分得

(10)

综合式(7)和式(10)得

(11)

假设作用飞机上的空气阻力是一个定值，则推力控制增量为

(12)

式(12)中：ΔT为推力增量，下标e表示参数的偏差量。由此，得到飞机总能量变化来控制推力Tc公式为

(13)

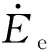
能量分配率用于保证动势能二者的同等控制优先级，它的含义是动势能变化率的差值，即

(14)

据此，得到升降舵偏角δec的控制律为

(15)

动能：

SKE = 0.5VTASVTAS

(16)

重力势能：

SPE=gH

(17)

动能变化率：

Erate=VTASVrate

(18)

势能变化率：

Prate=gVz

(19)

式中：VTAS为真实空速；Vrate为真实空速变化率；H为高度；Vz为高度变化率。

对于油门控制，建立一套油门和能量变化率之间的线性对应表，油门包括最小油门、平飞巡航油门和最大油门，分别对应了能量减小最大速率、0、能量增加最大速率。通过计算总能量变化率，即可线性计算出目标油门值。在此基础上，利用目标能量和当前能量，通过PID控制器对目标油门动态修正。

对于升降控制，将动能和重力势能进行分配，建立一个能量分配权重W，W可在0～2变化。即当W=0时，放弃速度控制，只控制高度；W=2时，放弃高度控制只控制速度；W=1时，既控制速度也控制高度，二者的权重是1∶1。然后根据目标能量分配和实际能量分配经过一个PID控制器，对刚才计算出来的目标俯仰角继续修正。

2 开源无人机软件

如图5所示，无人机的飞行仿真主要使用开源飞控软件PX4[11]，开源地面站QGroundControl[12]和开源飞行模拟器Flightgear[13]。

图5 无人机飞行仿真软件Fig.5 UAV flight simulation software

开源飞控就是建立在开源思想基础上的自动飞行控制器项目(open source auto pilot)，同时包含开源软件和开源硬件，而软件则包含飞控硬件中的固件和地面站软件两部分。

Pixhawk是近些年面世的一款开放源代码的无人机飞行控制系统的硬件部分，PX4是Pixhawk的原生固件，它的架构非常清晰，容易维护，主要优点是高效灵活，其传递消息的延时也相对低，主要使用C++开发，代码的封装比较复杂，理解上有一定的难度，支持非常丰富的无人设备，如多旋翼、固定翼、VTOL、小车、水下航行器、飞艇等。

QGroundControl是一款适用于非业余人员使用的无人飞行器的地面站软件，如果无人机采用MAVlink[14]，就可以使用QGroundControl制定航线、改变航路点和遥控飞行状态等功能。该软件功能完备，可以在飞行地图上显示出无人机的实时位置，便于用户掌握实时飞行状况，同时可以显示飞行轨迹、各个航点、飞行仪表盘、飞行速度高度等飞行参数，还可以叠加仪表视图的视频流显示，并且可在Linux、Windows、IOS、OSX、Android等系统上运行。

FlightGear是一个始于1997年多平台飞行模拟器、自由软件项目，它的源代码是开放的。使用OSG和C++语言开发，从最初粗糙的空气动力学模型开始，逐渐引入了自然特性(阳光、月光和星光等)、天气特性(云、雾和风等)、平显、仪表板、电子导航系统、机场与跑道以及网络互联操作等众多的特性。

3 无人机飞行仿真

3.1 仿真配置及实现

在仿真的环境中，仿真模拟器中允许PX4 飞行代码来控制计算机建模的无人机。可以与模拟的无人机进行交互，就像可以使用 QGroundControl与真正的无人机进行交互一样。PX4 支持软件在环(software-in-the-loop，SITL)仿真，此时PX4飞行软件运行在电脑上，支持硬件在环(hardware-in-the-loop，HITL)仿真。采用HITL时，PX4软件运行在真实的飞行控制电路板上。故仿真采用SITL仿真。

仿真模拟器使用仿真模拟的MAVLink 应用程序接口与之通信。该应用程序接口定义了一组MAVLink消息，用于提供从仿真世界中获取到的传感器数据到PX4，同时返回来自飞行控制代码的油门和操纵舵面数值，并应用于仿真的无人机。通常，PX4使用建立起来用于MAVLink的UDP端口，与地面控制站进行通联，地面站采用QGroundControl。PX4的远程UDP端口使用14450端口，QGroundControl地面站则默认监听该端口。

启动PX4的仿真，只需要下载PX4源码，并编译执行仿真模拟器对应的代码即可，对应于Flightgear的仿真模拟器运行代码如下：

make px4_sitl_nolockstep flightgear_rascal。

随后，Flightgear启动，并自动加载标准构型的固定翼飞机Rascal RC模型。再启动QGroundControl地面站，绘制无人机航线，上传到PX4飞行软件当中，如图6所示。然后，通过QGroundControl启动飞行仿真即可。此仿真系统的具体配置如下：Ubuntu 18.04操作系统，PX4固件版本为v1.11.0，QGroundControl版本为稳定版本4.0，Flightgear版本为1:2020.3.8-0ubuntu1～ppa1～21.04.1。

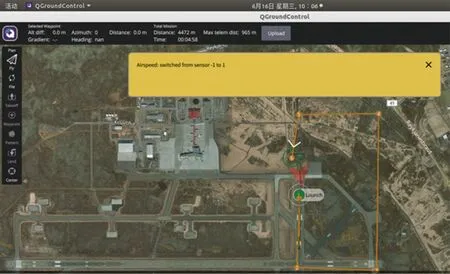
图6 使用QGroundControl地面站规划无人机航线并上传PX4飞行软件的界面Fig.6 Use QGroundControl ground station to plan UAV routes and upload PX4 flight software

飞行控制仿真主要参数设定见表1和表2。

表1 L1控制参数Table 1 L1control related parameters

表2 TECS控制参数Table 2 TECS control related parameters

3.2 仿真结果

图7所示为无人机飞行仿真的效果图，图7(a)是QGroundControl上实时显示的无人机沿航线飞行情况，图7(b)是Flightgear中无人机飞行视景实时显示。

图7 飞行仿真效果图Fig.7 Flight simulation renderings

如图8所示，定义无人机起飞点为坐标原点，北向为X轴，东向为Y轴，绘制得到无人机横向航线与实际飞行轨迹的对比图，能够直观显示无人机的横向L1的控制效果。

图8 无人机横向控制效果直观显示Fig.8 Intuitive display of UAV lateral control effect

结果显示，L1控制和总能量控制均达到了较为理想的控制效果，所构建的飞行仿真系统能够有效地对飞行控制算法进行验证，具有源代码可控、显示直观、数据分析方便的特点，包括对无人机姿态控制算法的改进以及参数的显示。

通过采集飞行仿真数据，可以进一步分析无人机的飞行参数。如图9所示为无人机三维轨迹的变化曲线，采用的是无人机相对起点距离。飞行数据均为无人机自动执行任务模态下产生。可以看到，所采用的轨迹控制算法控制效果较好，高度仅在爬升到指定高度时略有超调，在无人机转弯时，有轻微波动。

图9 无人机相对起点的三维轨迹变化Fig.9 The three-dimensional trajectory change of the UAV relative to the starting point

如图10所示为无人机的姿态控制效果图，可以看到，无人机在起飞前，飞行控制器估计的俯仰角与设定值存在10°的误差，起飞后逐渐恢复正常，这导致无人机跟踪出现超调。

图10 无人机姿态控制曲线Fig.10 UAV attitude control curve

如图11所示为无人机空速的跟踪效果和TECS算法对无人机高度变化率的跟踪，无人机起飞时，由于俯仰角的估计误差，导致高度变化率跟踪过程出现震荡。

图11 无人机速度和高度变化率控制Fig.11 UAV airspeed and height rate control

4 结论

通过分析设计无人机侧向和纵向的轨迹控制算法，完全使用开源系统和软件，采用软件在环的仿真技术，搭建了一套固定翼无人机飞行仿真系统，并通过该系统验证了无人机轨迹控制算法，取得了理想的实验效果。其中，仿真系统完全自主可控，显示直观，数据分析便捷，为后续无人机复杂飞行控制算法的仿真验证提供了基础平台。