非饱和土广义有效应力三剪强度准则及验证
路祥,胡小荣
(南昌大学工程建设学院,江西 南昌 330031)
非饱和土的强度准则与所采用的有效应力原理有关,张常光等[1-2]在双剪强度准则的基础上采用双应力变量法提出了双应力变量法的非饱和土双剪强度准则,该准则对真三轴试验数据取得了很好的计算预测结果,但存在双重破坏角现象[3]。鉴于三剪强度准则[4-5]所具有的优点,陈昊等[6]基于单应力变量法和双应力变量法提出了非饱和土的三剪强度准则,并验证了所提准则的合理性。单应力变量法[7]存在有效应力系数难以确定并且和饱和度对应关系不唯一的问题[8-9]。Burland等[10]还发现非饱和土在基质吸力减小的过程中会发生湿陷变形,但如果采用单应力变量法则会得到土体发生体积膨胀的结果。双应力变量法[11]最明显的缺点就是无法考虑饱和度的影响[12]且无法描述土体从非饱和状态到饱和状态间的平稳过渡[13-14],原因是双应力变量有效应力原理在非饱和土基质吸力为零时不能与饱和土的有效应力原理相衔接。赵成刚等[15-17]提出了非饱和土的广义有效应力原理,在非饱和土总的变形功表达式中得到了与土骨架位移在功上对偶的有效应力表达式,能考虑饱和度对非饱和土体性质的影响。广义有效应力(也称为平均土骨架应力[18])是基于混合物理论和多相孔隙介质力学推导而来,具有科学的理论基础[19]。
为克服上述屈服准则、单应力变量法和双应力变量法的不足,本文采用广义有效应力变量法,将其与三剪强度准则[4-5]相结合,得到非饱和土广义有效应力三剪强度准则。新的强度准则可以反映土体的中间主应力效应、拉压不等效应、区间效应,还可以考虑黏聚力、基质吸力、饱和度对土体强度的影响,能够更好地反映土体的真实情况,并进一步拓宽非饱和土破坏强度理论。最后对该强度准则进行π平面极限线和在p′-q平面子午线特征分析及正确性验证。
1 非饱和土广义有效应力三剪强度准则及特征分析
1.1 强度准则表达式
将非饱和土广义有效应力[15]代入到三剪强度准则[4-5]中,得到基于广义有效应力的非饱和土三剪强度准则为
(1)
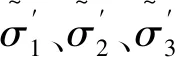
非饱和土广义有效应力具体表达式[15]为
(2)
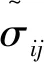
(3)
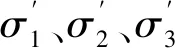
(4)
净主应力及其相关的应力不变量关系式[20-21]为
(5)
式中:p′为平均净主应力;q为广义剪应力;ρ为π平面上极限线上的点到静水压力轴的垂直距离。将式(5)代入式(4),得
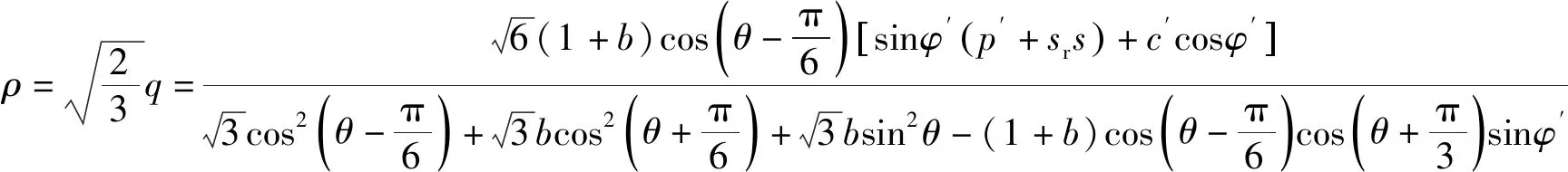
(6)
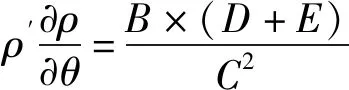
(7)
其中
由式(6)得到强度准则p′-q子午线表达式为
q=A[(p-pa+srs)sinφ′+c′cosφ′]=
Asinφ′p′+A(srssinφ′+c′cosφ′)
(8)
其中

1.2 强度准则特征分析
由式(6)和文献[22]的相关数据可作出强度准则在π平面上的极限线,如图1所示。其中,图1(a)是在s=100 kPa,sr=34.5%,p′=300 kPa,不同b值影响下的π平面极限线;图1(b)是在b=0.25,s=100 kPa,sr=34.5%,不同平均净主应力p′影响下的π平面极限线;图1(c)是在b=0.50,s=100 kPa,sr=34.5%,不同平均净主应力p′影响下的π平面极限线;图1(d)是在b=0.25,p′=300 kPa,不同基质吸力s影响下的π平面极限线;图1(e)是在b=0.50,p′=300 kPa,不同基质吸力s影响下的π平面极限线。
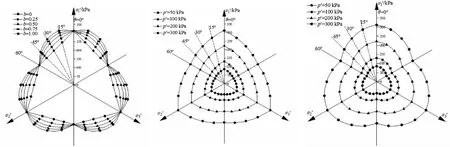
(a) 不同b值影响 (b) b=0.25,s=100 kPa (c) b=0.50,s=100 kPa
由图1(a)可知,当只有中主应力影响系数b值改变时,不同的b值所对应的π平面极限线在三轴拉伸状态(也即是θ=60°时)通过60°坐标轴线上的同一点Q。其中的某一个b值所对应的π平面极限线在Q点与60°坐标轴线相垂直,这时的中间主应力影响系数b值设为b0。当b0≤b≤1.00时,这时的b值所对应的π平面极限线就是非外凸型极限线[20],当0≤b≤b0时,这时b值所对应的π平面极限线就是外凸型极限线[20]。根据条件b0值所对应的π平面极限线与θ=60°坐标轴相交于Q点,且在Q点与60°坐标轴相垂直,方程式如下
(9)
将θ=60°代入到式(9)中得
(10)
由式(10)得
ρ′=0
(11)
由式(7)和式(11) 得到b0为
(12)
将φ′=27.92°代入到式(12)中计算得到b0=0.15。
由图1(b)和图1(c)可知,在中间主应力影响系数和基质吸力一定的情况下,随着平均净主应力的增大,π平面极限线逐渐向外扩展延伸,即平均净主应力越大,所对应的破坏应力也就越大,这与实际净平均主应力的增大可以提高土体的强度的土体受力情况一致。不同的平均净主应力所对应的π平面极限线离得很远,说明平均净主应力对土体的破坏强度影响程度非常大。同时不同的平均净主应力所对应的π平面极限线形状一致,也即平均净主应力只改变π平面极限线的大小,而不改变它的形状。由图1(d)和图1(e)可知,在中间主应力影响系数和平均净主应力一定的情况下,随着基质吸力的增大,π平面极限线逐渐向外扩展延伸,即基质吸力越大,所对应的破坏应力也就越大。由图1(d)和图1(e)对比可知,基质吸力和平均净主应力相同的情况下,b取不同的值,所对应的π平面极限线不仅大小不一样,形状也会发生变化。
由式(8)和文献[22]数据可作出强度准则在p′-q平面上的子午线,如图2所示。在基质吸力s=100 kPa,饱和度sr=34.5%,中间主应力影响系数b值分别取0.25和0.50和在基质吸力s=200 kPa,饱和度sr=25.4%,b=0.25这3种不同的情况下,根据式(8)计算后分别作出强度准则在p′-q平面上的子午线,如图2所示。

p′/kPa(a) b=0.25,s=100 kPa
由图2可知,在p′-q平面中,随着θ角的增大,子午线的斜率相应变小。不同的lode角所对应的子午线在p′负半轴相交于同一点。当基质吸力s和饱和度sr保持为定值而b值不同的情况下,中间主应力影响系数b值的改变对θ=30°子午线产生影响。当b=0.25时,纯剪切(θ=30°)p′-q平面子午线非常接近于常规三轴拉伸(θ=60°)p′-q平面子午线;当b=0.50时,纯剪切(θ=30°)p′-q平面子午线靠近于常规三轴压缩(θ=0°)p′-q平面子午线。
2 强度准则真三轴验证
为了验证本文新建立的广义有效应力变量法非饱和土三剪强度准则的正确性,将文献[22-24]中的真三轴数据分别与本文的计算结果进行对比验证,来验证所提准则的正确性。
基质吸力s=100 kPa,平均净主应力p′分别为100,200,300 kPa,有效黏聚力c′=5.3 kPa,有效内摩擦角φ′=27.92°。根据文献[20]计算可得s=100 kPa时所对应的饱和度sr=34.5%。本文所提出的新准则预测值与试验结果对比,如图3~图5所示。
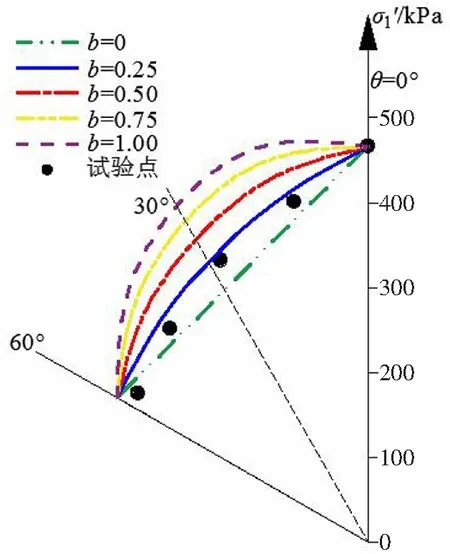
图3 不同b值π平面极限线Fig.3 Limit lines in the plan of π plane with different b values
由图3可知,在平均净主应力和基质吸力一定的情况下,随着中间主应力影响系数的增大,π平面极限线逐渐向外扩展延伸,当b=0.25时所对应的π平面极限线最接近试验的结果,所以取b=0.25最适合。
由图4可知,取b=0.25的非饱和土广义有效应力三剪强度准则计算预测结果与试验结果较为吻合,验证了本文所推导的新准则的正确性。新准则采用了广义有效应力原理,具备广义有效应力原理的优点,考虑了饱和度的影响,可以更全面地描述非饱和土的力学特性。

图4 广义有效应力变量法计算结果和试验数据对比图Fig.4 Comparison diagram of calculation reults of generalized effective stress variable method and test data
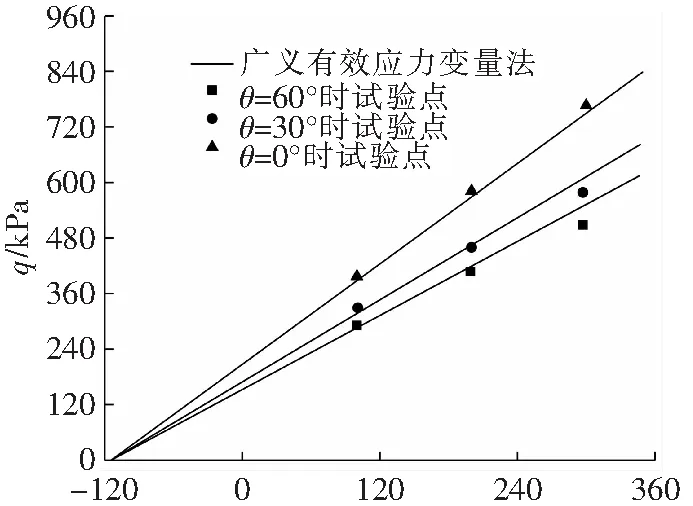
p′/kPa图5 子午线计算结果与试验数据对比图Fig.5 Comparison diagram of meridian calculation results and experimental data
由图5可知,广义有效应力法预测的p′-q子午线与试验点相比对,试验点基本与广义有效应力法下的p′-q子午线吻合,新准则取得很好的预测效果。
Hoyos等[23-24]对非饱和黏土砂做了真三轴试验,试验所用的黏土砂有效黏聚力c′=0 kPa,有效内摩擦角φ′=30°,基质吸力s=200 kPa,根据文献可得平均饱和度sr=37.5%,平均净主应力p′=100 kPa。本文所提出的新准则预测值与试验结果对比,如图6~图8所示。
由图6可知,基质吸力和平均净主应力相同的情况下,b取不同的值,所对应的π平面极限线形状会发生变化,并且随着b值的增大逐渐向外扩展延伸。试验点介于b取0.75和1.00的π平面极限线之间,虽然实验点更接近于b取1.00时的π平面极限线,但出于安全考虑,取0.75更能保证安全。所以b取0.75最适合。
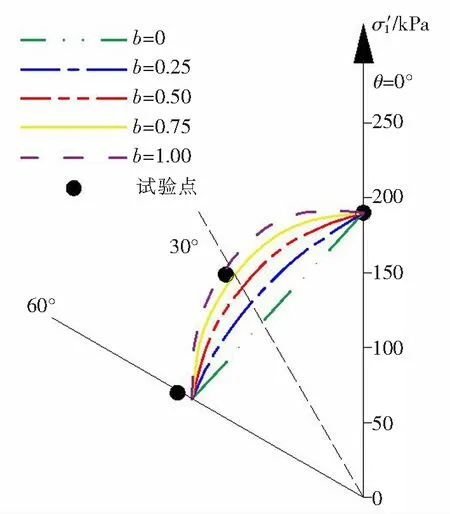
图6 不同b值的π平面极限线与试验点对比图Fig.6 Comparison diagram of π plan limit lines with different b values and test data

图7 广义有效应力变量法计算结果和试验数据对比图Fig.7 Comparison diagram of calculation reults of generalized effective stress variable method and test data

p′/kPa图8 子午线计算结果与试验数据对比图Fig.8 Comparison diagram of meridian calculation results and experimental data
由图7可知,将本文所推导的破坏准则预测结果与单应力变量法和双应力变量法的三剪强度准则预测结果相比较,可以得到广义有效应力变量法最为吻合试验结果,同时和双应力变量法比较接近。单应力变量法预测误差更大。新准则虽未对双应力变量法三剪强度准则产生明显的优势,但其采用了广义有效应力原理,能更全面地描述非饱和土的力学特性。
由图8可知,将广义有效应力法预测的p′-q子午线与试验点相比对,文献中的试验数据点比较少,试验点基本与θ=0°的广义有效应力法下的p′-q子午线吻合,新准则取得很好的预测效果。
3 结论
将广义有效应力原理与三剪强度准则相结合,推导了非饱和土广义有效应力三剪强度准则,并对其进行了π平面极限线和在p′-q平面子午线特征分析及正确性验证。结论如下:
(1)用非饱和土广义有效应力表达式代替三剪强度准则中的有效应力,从而推导得出基于广义有效应力变量法的三剪强度准则。根据非饱和广义有效应力三剪强度准则表达式作出了它在π平面上的极限线和p′-q平面上的子午线,并对其进行了特征分析,并通过计算得到了它在π平面外凸型极限线和非外凸型极限线的分界b0值。
(2)将本文所推导的非饱和土广义有效应力三剪强度准则对文献[22]的非饱和黄土真三轴试验数据和文献[23-24]的非饱和黏土砂真三轴试验数据进行验证,取得了很好了验证效果,预测结果和试验数据基本吻合,证明了所推导准则的正确性。
(3)非饱和土广义有效应力三剪强度准则计算预测结果接近试验的结果,能够很好地反映土体的真实情况,有效地扩宽了非饱和土破坏强度理论。同时它继承了三剪强度准则的优势,能更好地描述非饱和土破坏强度,是一系列统一破坏准则,只要通过取不同的b值就可以得到不同的准则,其他准则都可以通过该准则作非线性逼近。
(4)b值是非饱和土广义有效应力三剪强度准则中非常重要的参数,该参数可以反映中间主应力对土体强度的影响。通过真三轴试验、非饱和土物理力学特性指标、真三轴应力角θ、p′-q平面子午线方程可以进行求解b值大小。

