地铁列车荷载作用下密接下穿隧道顶板结构动力响应分析

郑龙超

（中铁隧道局集团建设有限公司，广东 佛山 528299）

0 引言

城市地铁逐渐跨入“环线+放射线”网状化运营时代，三线以及四线换乘车站日益增多，导致地铁轨行区下穿既有运营地铁车站，运营列车荷载频繁作用影响了下穿隧道顶板结构的安全。

地铁列车振动荷载是一种长时间往复施加的特殊循环荷载，部分学者通过改变单或双列车动载、隧道空间形式等，得出了不同工况下隧道的结构动力响应特征及规律[1-3]。陈行等通过改变围岩等级及隧道间距等因素，得出了交叉隧道振动加速度大小、损伤区域及主应力变化等[4]；晏启祥等通过改变隧道净距，得出了拟合列车荷载下交叉隧道动力响应影响区等[5]。国内外学者虽然已对交叉隧道列车振动影响特征进行了研究[6-9]，但多为近距离交叉隧道，运营隧道间夹有岩土体，具有消减列车振动荷载的作用，而对地铁列车循环荷载作用下，密接下穿地铁车站动力影响的研究较少。

因此，该文依托成都地铁倪家桥站，采用有限元动力学计算方法，进行了不同地铁列车运行速度对密接正交下穿隧道顶板结构动力响应特征的分析。

1 工程概况

1.1 下穿隧道与既有车站的位置关系

成都地铁8号线倪家桥站位于人民南路和倪家桥路交汇处，其轨行区及换乘通道密接下穿既有1号线车站，平面布置图如图1所示。8号线换乘通道结构形式为矩形，宽度为23.4m、高度为9.05m，既有运营1号线车站长163.5m、宽18.7m。地铁1号线采用中车四方车辆有限公司制造的4动卡2拖卡6节编组B型列车，每节列车高度为3.8m、宽为2.8m，长度为19.52m，车辆定距为12.6m，固定轴距为2.1m，轴重14t，列车运行振动对下穿隧道顶板结构的动力响应尚不明确。

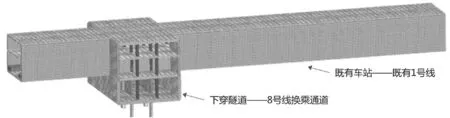
图1 下穿隧道与既有车站位置关系

1.2 工程地质

工程场地基岩为白垩系灌口组紫红色泥岩，下穿隧道上半部分位于中密卵石土层，下半部分位于强风化泥岩，底板下2m~3m为中风化泥岩。地下水赋存于基岩裂隙中，含水量较小。

2 数值计算概况

2.1 模型建立

动力分析模型尺寸的确定：综合考虑三维有限元模型中土体与结构的位置关系，取土体的边界至隧道侧壁的距离尺寸为隧道直径的3倍~6倍，振动波可均匀向外传播扩散。

模型边界范围：水平方向取既有1号线车站长度，宽度取8号线下穿通道与上部车站相交的长度，底部边界至下部车站底板距离30m，土体采用摩尔-库伦模型，其余结构均采用弹性模型。模型范围为X×Y×Z＝160m×38.1m×56m，有限元模型如图2所示。

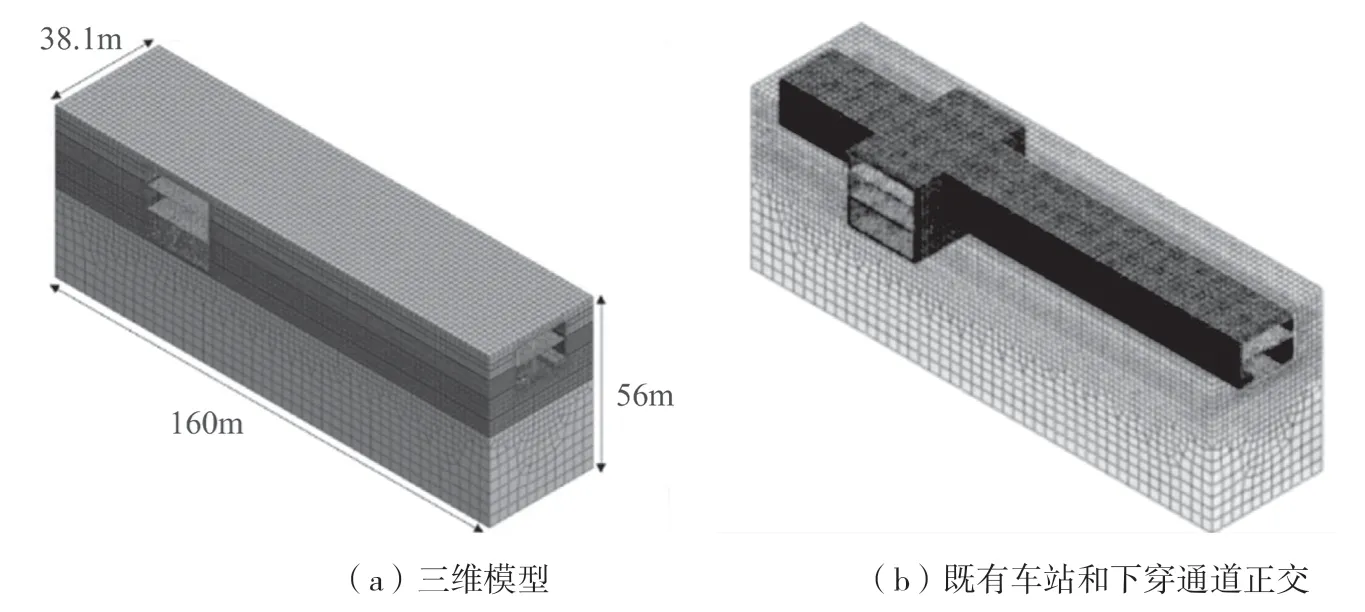
图2 三维数值计算模型

2.2 计算参数选取

地层及车站结构的物理力学参数见表1。

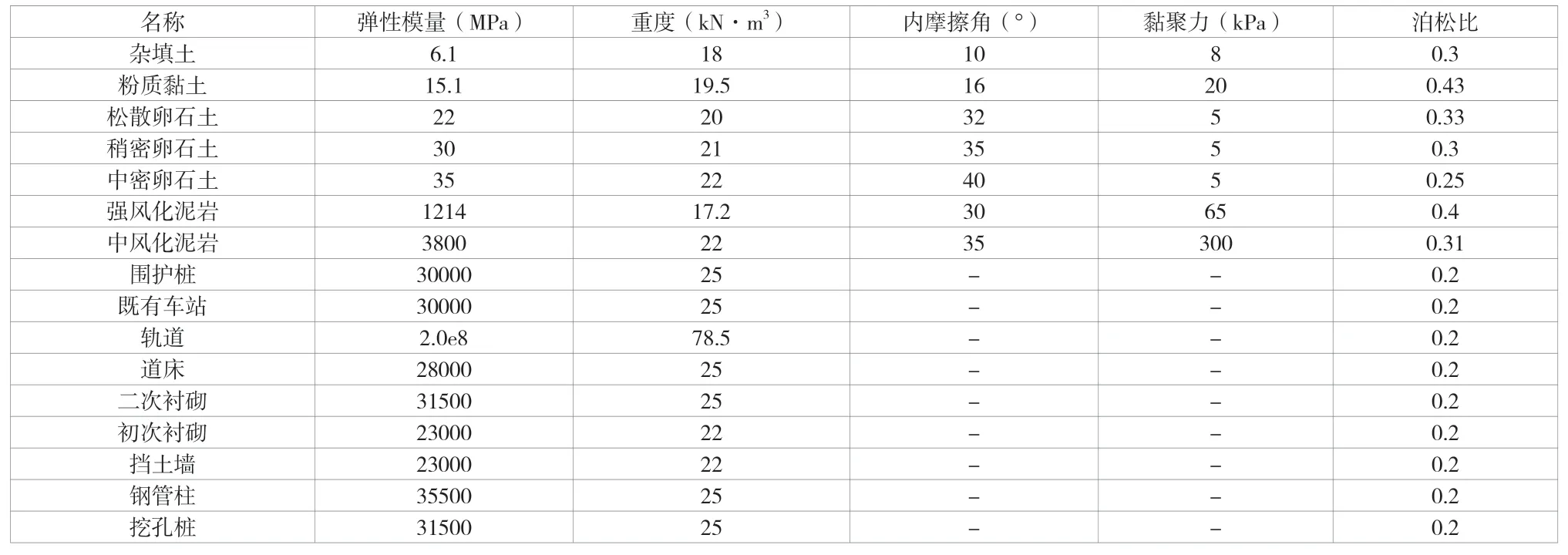
表1 模型主要力学参数

2.3 边界条件及阻尼比确定

2.3.1 边界条件

计算模型采用黏性边界来模拟无限地基，在模型周边和底部设置阻尼元件，并在土体底部生成限制X、Y、Z三个方向平动自由度的约束。计算了整体三维有限元模型的前100阶特征周期值，得到特征值分析的第一和第二主振型的周期，分别为0.672s和0.466s。

2.3.2 阻尼比

为实现建筑物的阻尼效果，采样模态阻尼，取阻尼比为0.03，结合第一和第二主振型的周期，取瑞利型阻尼的阻尼质量系数a=0.3313，b=0.0026。

2.4 列车荷载确定

成都地铁1号线采用中车四方车辆有限公司制造的4动卡2拖卡6节编组B型列车，生成列车荷载如图3（a）所示。动力分析时取10s时长加载，考虑右轨线地铁匀速行驶，将列车动荷载施加在右轨线轨道上，施加形式如图3（b）所示。

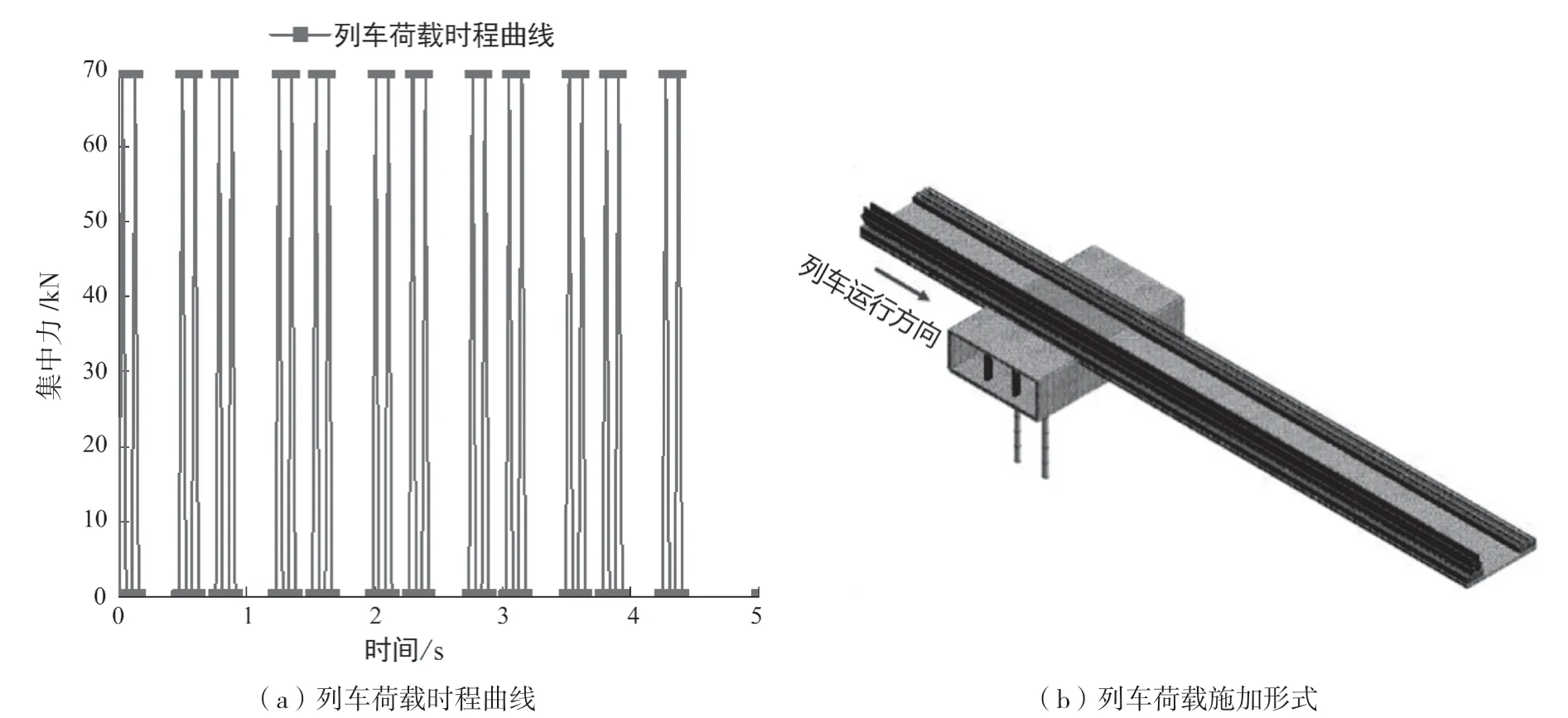
图3 地铁列车荷载特征

2.5 模拟工况

针对地铁行驶速度建立不同工况，对比分析不同地铁列车时速对下穿隧道顶板的动力响应特性，各工况列车时速分别为80km/h、100km/h、120km/h、140km/h。

3 下穿隧道顶板结构动力响应特征

3.1 特征点的选取

选取下穿隧道衬砌顶板进行分析，并选取3个特征点位，分别为8号线车站中轴线与1号线车站左轨线、中线和右轨线交叉处，即A、B和C处，如图4所示。并把特征点A在列车时速80km/h的动力响应为“A-80”，其他特征点表示方法相同。

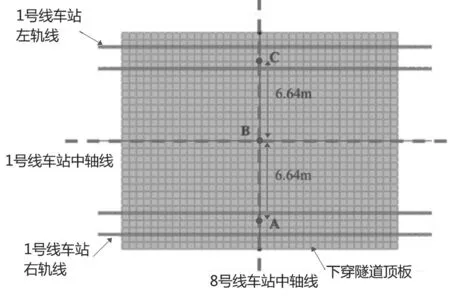
图4 特征点位选取

3.2 位移响应特征

根据不同地铁时速计算结果，绘制不同速度工况下各特征点的竖向变形时程曲线和竖向位移峰值，如图5和表2所示，正值为向上位移，负值为向下位移。

由图5和表2可知，各特征点竖向变形时程曲线变化规律相似。特征点越靠近列车运行轨线，受列车振动影响就越大。从列车运行开始，特征点开始受到列车振动，到第一个车轴经过特征点时，顶板沉降变形增量较大，到最后一个车轴经过特征点时，沉降增大量减少；特征点A受列车动载影响最大，竖向位移峰值为-0.035mm，是特征点B的2.5倍，特征点C的5.8倍。在地铁运行10s内，由于列车作用力相同，因此地铁时速越快，各特征点作用时间就越短，也就会使特征点在越短时间内的变形量达到最大值。

表2 各特征点的竖向位移峰值（mm）

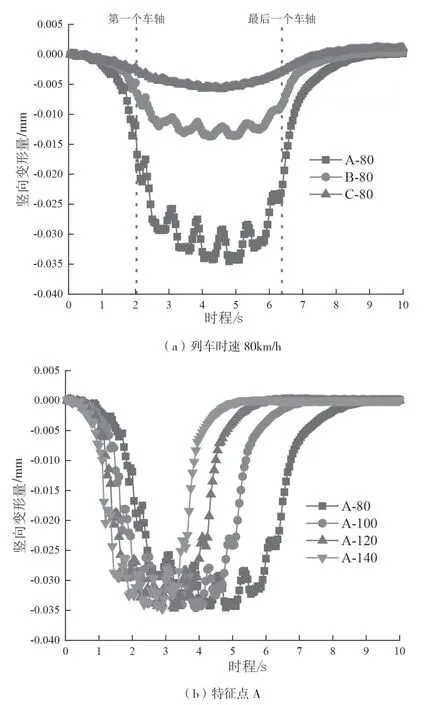
图5 各特征点的竖向变形时程曲线

3.3 速度响应特征

根据不同列车时速下模型计算结果，绘制不同工况下各特征点的竖向速度时程曲线和竖向速度峰值，如图6和表3所示，正值为向上移动，负值为向下移动。

由图6和表3可知，各特征点竖向速度时程曲线变化规律相似。从列车开始出发，特征点竖向速度幅值开始增长，当第一个车轴经过特征点时竖向速度幅值最大，到达峰值，然后降至一定幅值后保持稳定，到最后一个车轴经过特征点时，竖向速度幅值逐渐降低趋于零值。特征点越靠近列车运行轨线，受列车振动影响就越大，其幅值也就越大，特征点A受列车动载影响最大，峰值为-0.165mm/s，是特征点B的2.95倍，特征点C的11倍。

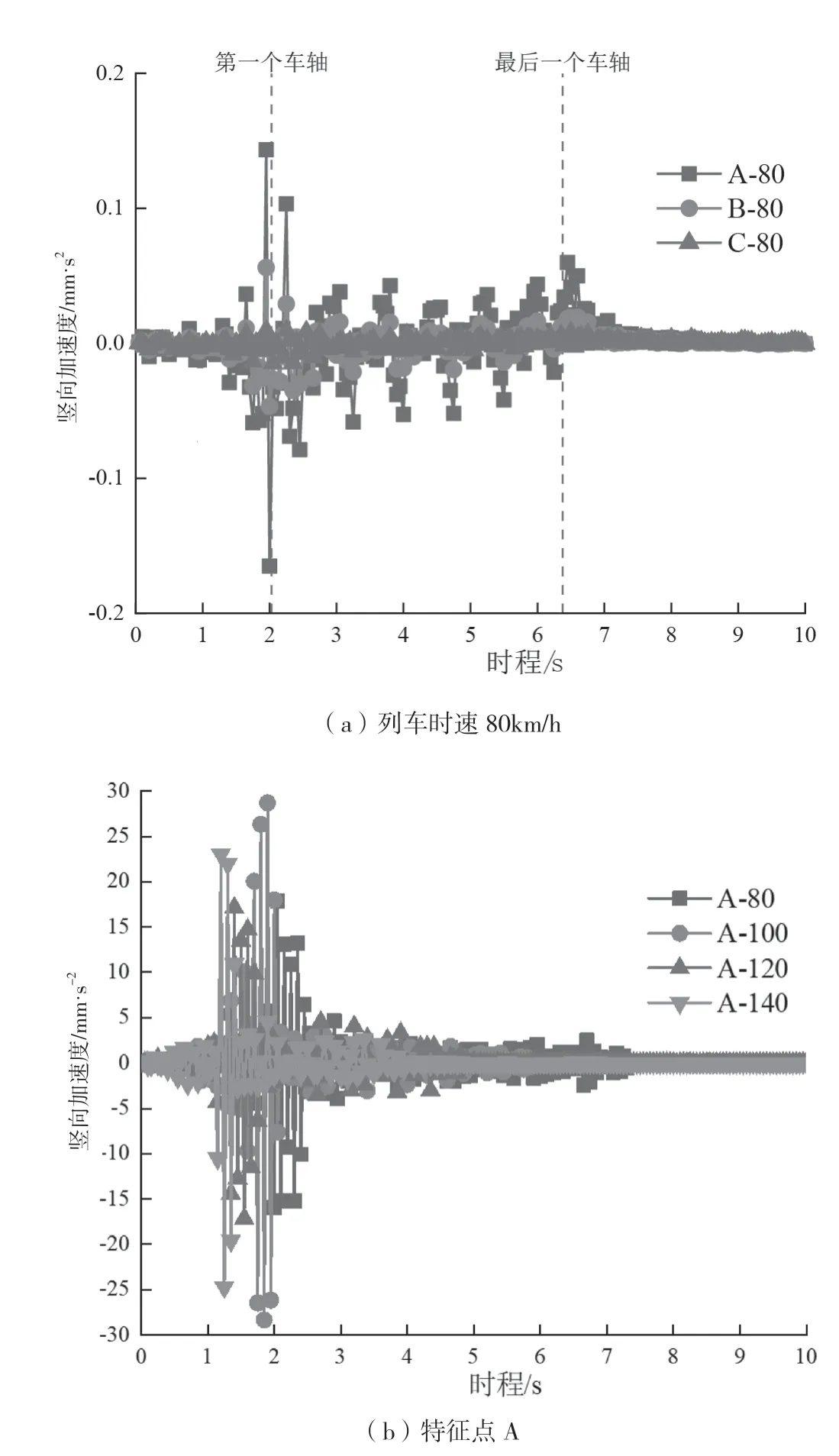
图6 各特征点竖向速度时程曲线

表3 各特征点的竖向速度峰值（mm·s-1）

不同时速情况下各特征点的竖向速度峰值均较小，相同时速时靠近列车运行轨线的特征点A峰值最大。当列车速度为100km/h时，峰值最大为-0.285mm/s，远小于容许值1mm/s，在顶板结构安全范围内。

3.4 加速度响应特征

不同列车速度工况下各特征点的竖向加速度时程曲线和加速度峰值如图7和表4所示，正值为向上振动，负值为向下振动。

表4 不同工况下各特征点的竖向加速度峰值（mm·s-2）

由图7和表4可知，各特征点时程竖向速度曲线规律相似。从列车开始移动，特征点竖向加速度增长，当第一个车轴经过特征点时竖向加速度幅值最大，然后降低至一定幅值后保持稳定，到最后一个车轴经过特征点时，竖向加速度幅值逐渐降低趋于零值；特征点越靠近列车运行轨线，受列车振动影响就越大，其幅值也就越大，特征点A受列车动载影响最大，峰值为-17.84mm/s2，是特征点B的3.25倍，特征点C的24.44倍。

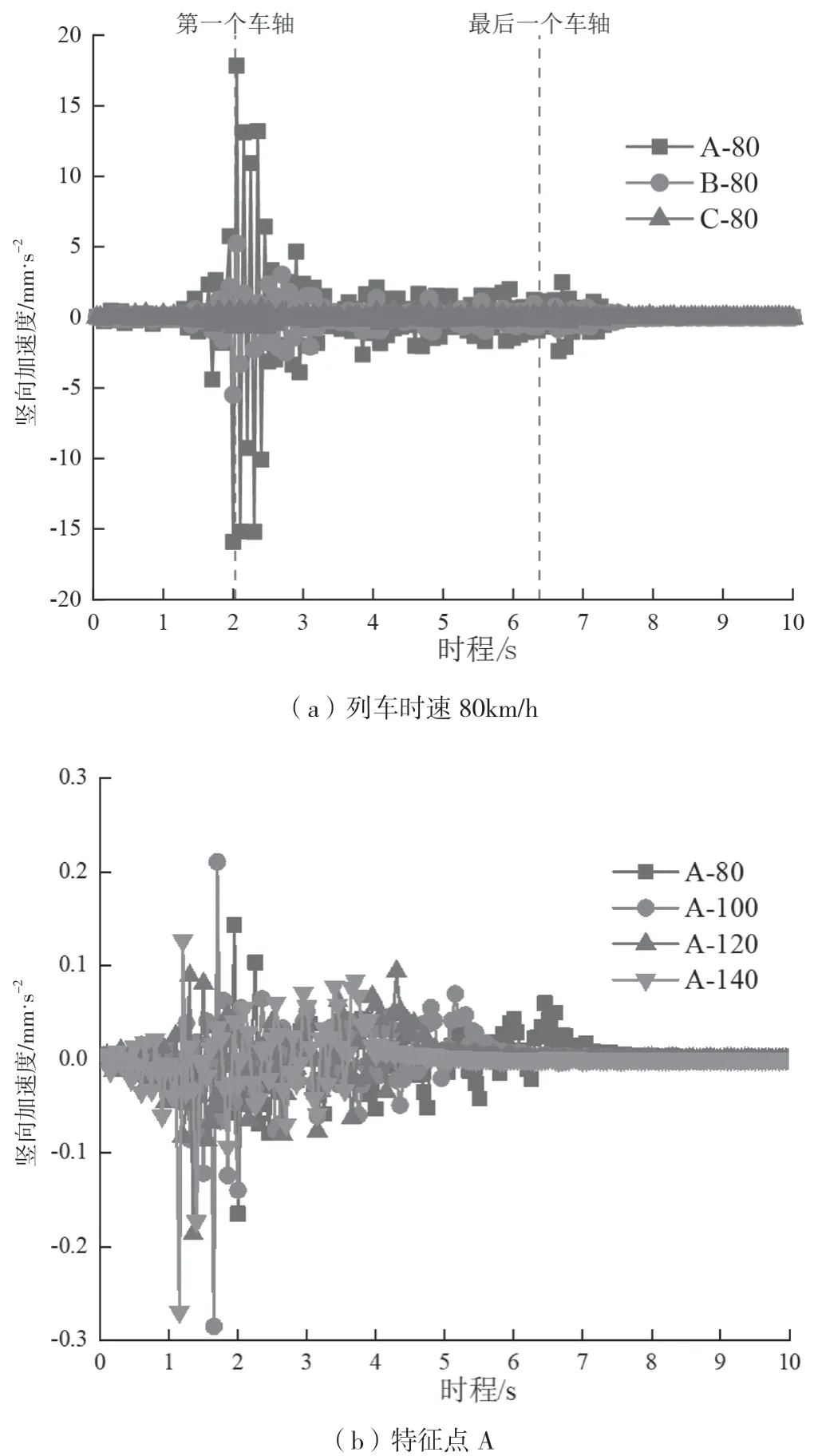
图7 不同工况下各特征点的时程竖向加速度曲线

各特征点的竖向加速度峰值均较小，靠近列车运行轨线的特征点A峰值最大。当列车速度为100km/h时，A点加速度峰值最大为-28.71mm/s2，远低于容许值500mm/s2，下穿隧道顶板结构在安全范围内。

3.5 应力响应特征

下穿隧道顶板应力最大主应力云图如图8所示。

由图8可知，当列车速度为80km/h时，隧道顶板最大主应力较大，量值为0.43MPa；当列车速度为120km/h时，顶板最小主应力峰值最大，值为-0.112MPa，满足混凝土强度要求。

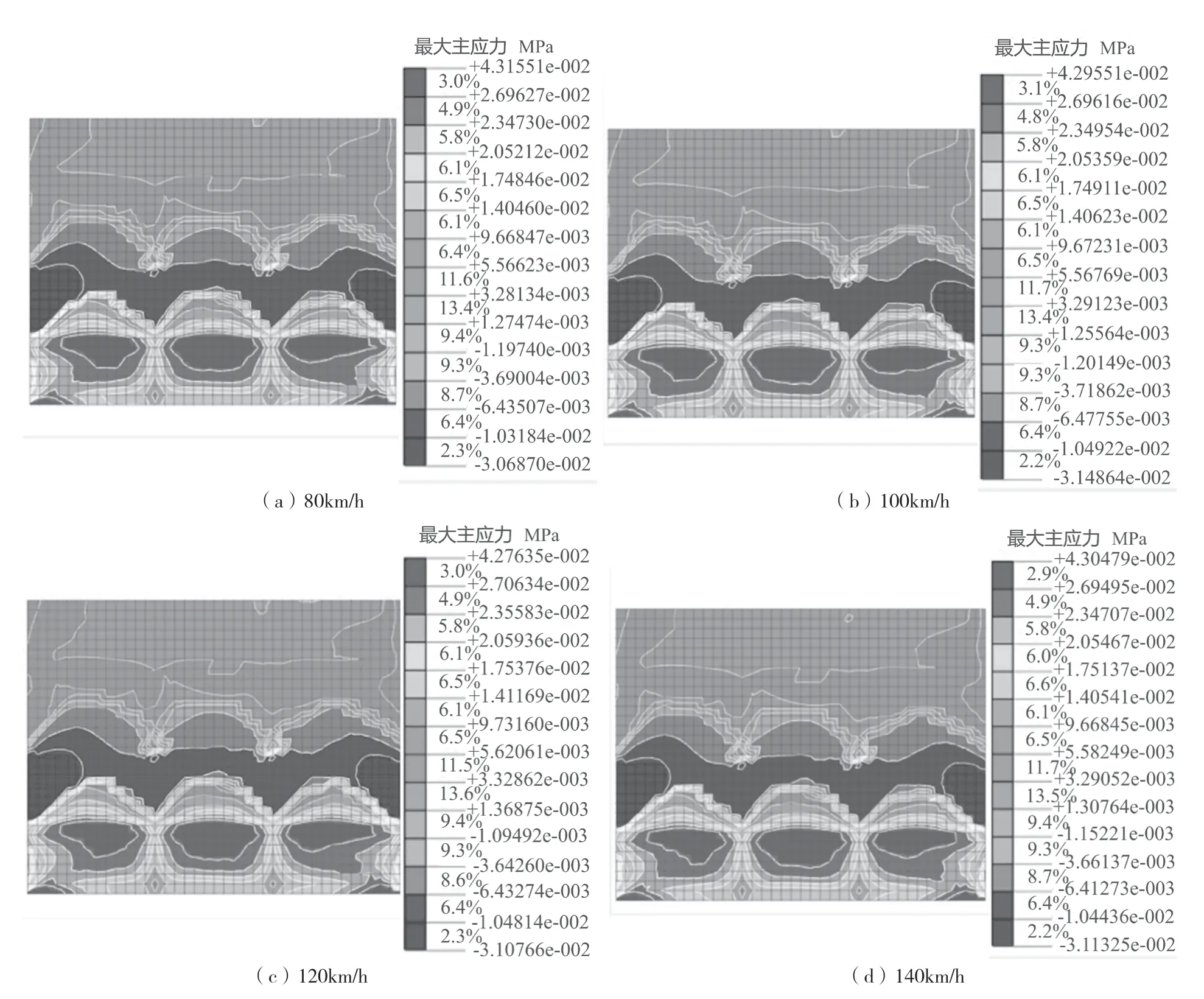
图8 下穿隧道顶板最大主应力云图（MPa）

4 结论

该文分析了不同地铁列车运行速度对密接下穿成都地铁1号线车站的隧道顶板结构动力响应特性，获取了下穿隧道顶板竖向位移、速度、加速度及应力等响应特征，得出的主要结论如下：1）当地铁列车运行速度为80km/h、100km/h、120km/h及140km/h等工况时，位于地铁车站底板下方隧道顶板振动力学响应均在容许值以内，隧道结构处于安全状态。2）下穿隧道顶板分析特征点越靠近列车运行轨线，受列车振动影响越大，且当第1对车轴作用达到特征点时动力响应最大，最后车轴作用后特征点动力响应逐渐消减。3）不同地铁列车运行速度对下穿隧道顶板结构最大响应特征影响不同，运行轨线下方动力响应明显，位移响应特征影响顺序为140km/h＞80km/h＞100km/h＞120km/h，最大变形位于下穿顶板跨中部；最大主应力响应特征影响顺序为80km/h＞140km/h＞100km/h＞120km/h，最大拉应力位于下穿隧道顶板中部，最大压应力位于顶板与侧墙相交处。