基于XGBoost与SHAP模型的特征分析在PM2.5浓度预测中的应用

张士杰，窦 燕

（新疆财经大学 统计与数据科学学院，新疆 乌鲁木齐 830012）

引言

现今，我国社会主义经济经历了飞速的发展。工业化和城市化也处于一个快速发展的阶段，与此同时能源的消耗也在大幅提升，致使空气中颗粒物的含量有了明显的增加，雾霾天气的出现也变得更加频繁[1]，严重阻碍着城市生态文明的建设。2019年《世界空气质量报告》中提出了空气污染仍是全球人口面临的最重要的环境健康风险之一，而大气颗粒物作为空气污染的首要物质，将直接对公民的健康和良好的生态环境造成巨大的威胁[2,3]。根据2012年我国生态环境部发布的《环境空气质量标准》（GB3095-2012），PM2.5可长时间悬浮于大气中，且具有吸收和散射可见光的能力，能够明显降低大气可见度[4]，致使区域性雾霾天气时常发生，进而影响区域空气质量甚至造成气候的变化[5]。PM2.5浓度作为评价空气质量的重要指标，不仅与大气污染息息相关，还对人体健康造成了重大危害[6]。因此，进一步提升PM2.5浓度的预测精度以及预测模型的可解释性，不仅可为区域空气质量预测和预警奠定基础，还可以减少PM2.5污染给社会造成的危害。

近年来，随着区域大气污染防治攻坚，协调推动经济高质量发展的提出，对PM2.5浓度的预测方法，主要可归纳为三类：确定性模型、经典的统计学模型和机器学习模型[7]。统计学预测方法主要有多元线性回归[8]、自回归移动平均[9]等模型。传统的统计学方法虽具有简易的结构和模型解释能力强等优点，但PM2.5浓度受到各种污染物的影响及其复杂的物理成因，这使得PM2.5浓度具有很强的非线性和时空分异性[10]。因此，单一的传统统计预测方法在处理非线性时序数据时，已无法得到较为理想的结果。

机器学习模型凭借自身优越的预测性能得到了广泛应用[11]，如支持向量机[12]和神经网络算法[13,14]等。其中，杜续等在解决神经网络预测模型中存在的易过拟合和低效率问题时，发现调整参数后的最优随机森林模型可对PM2.5进行有效地预测并具有较好的运行效率[15]。为进一步提高模型的预测性能，Park S等通过建立ANN模型，对地铁站的PM10浓度进行预测，精度达到了67%-80%[16]。康俊锋等提出XGBoost-LSTM的组合模型，研究发现该模型可以很好地结合PM2.5浓度数据的时序特征和非线性特征，进而提升模型的预测精度[17]。

以上研究只关注了模型的预测性能，而在模型可解释性方面的关注较少。已有利用集成算法和组合模型的预测研究相比传统的统计预测模型，性能更为出色，但同样存在两点不足之处：（1）随着预测模型复杂度的增加，当数据样本量不足时，容易出现模型泛化能力较差的问题。（2）随机森林、神经网络及XGBoost-LSTM均为黑箱机器学习模型，这使得建立的预测模型缺乏可解释性。为了解决以上研究存在的两点不足，在对原始数据进行预处理、模型迭代训练、超参数调优、模型泛化和性能分析以及模型解释等工作的基础上，本文基于XGBoost建立了PM2.5浓度预测模型，通过对比实验，验证了本文模型性能的优越性，并利用Grid Search CV技术进行超参数调优，进一步提高了PM2.5浓度预测的精度。同时由各模型的学习曲线对比结果，证明了在样本量较少时，本文模型同样拥有良好的泛化能力。为增强模型的可解释性，在利用XGBoost算法确保模型性能的基础上，引入SHAP模型，综合各特征的SHAP值识别出了PM2.5浓度的关键影响因素。其结论可为区域空气污染治理提供有价值的决策参考。

1 模型与方法

1.1 问题模型分析

设X为预测因子样本集合(包括：PM10、SO2、NO2、O3、CO等特征)，Y为PM2.5浓度，给定数据的训练集为：D={(xi,yi),(x2,y2),…,(xn,yn)}，其中，xi=(xi(1),xi(2),…,xi(p))和p分别表示为输入的样本实例和特征个数，i=1,2,…,n，n为样本个数。使用均方误差∑(yi,y^i)2表示预测误差，由Min_MSE准则求解最优输出值。将原数据集进行数据预处理后，将训练样本输入XGBoost模型进行迭代运算。XGBoost算法是由陈天奇等人近年研发的Boosting库[18]，拥有线性规模解析器和CART算法，已应用于许多的实际场景且具有良好的性能[19,20]。该算法在运行过程中的关键在于不断地添加树，每添加一棵树的实质相当于学习一个新的函数，来拟合前一次预测的残差。它是在传统的GBDT算法（只利用一阶倒数）上的改进，可选用CPU进行多维并行计算，完成更高的精度需求。为了改善目标函数的下降和模型的复杂度，XGBoost对损失函数进行了合理的二阶泰勒展开，同时引入正则项，对算法整体求其最优解，进而避免过拟合。为了训练得到PM2.5浓度预测模型，融合XGBoost算法建立模型，其中关键的模型构建步骤如下：

（1）给定n个样本，p个特征的PM2.5预测因子数据集：D={(xi,yi)}(|D|=n.xi∈R），利用迭代K次的输出结果作为提升树模型。对于第i个PM2.5浓度样本xi的预测浓度表示为，表达式为：

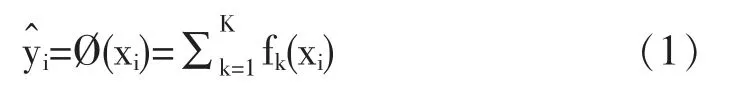
（2）PM2.5浓度预测模型训练过程中的损失函数的计算公式如下式(2)(3)所示：

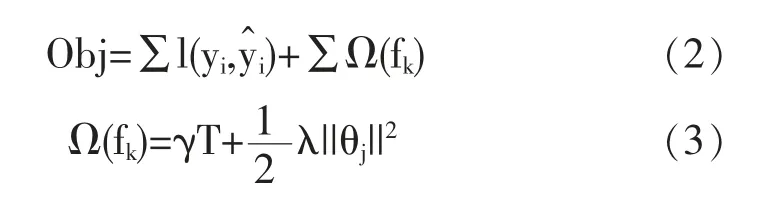
上述(2)式中，∑l(yi,)、∑Ω(fk)分别表示损失函数、正则化项，其中，yi表示PM2.5浓度的真实值，为预测输出值，T、θj、γ分别为树叶子节点数、叶子权重和叶子树惩罚正则项，λ为子权重惩罚正则项。

（3）在模型训练中采取梯度提升策略，保存已形成的模型，每次在模型中添加一个新的回归树，假设第i个PM2.5浓度样本在第t轮迭代的预测结果为，fi(xi)为引入的新回归树，其推导过程如下：

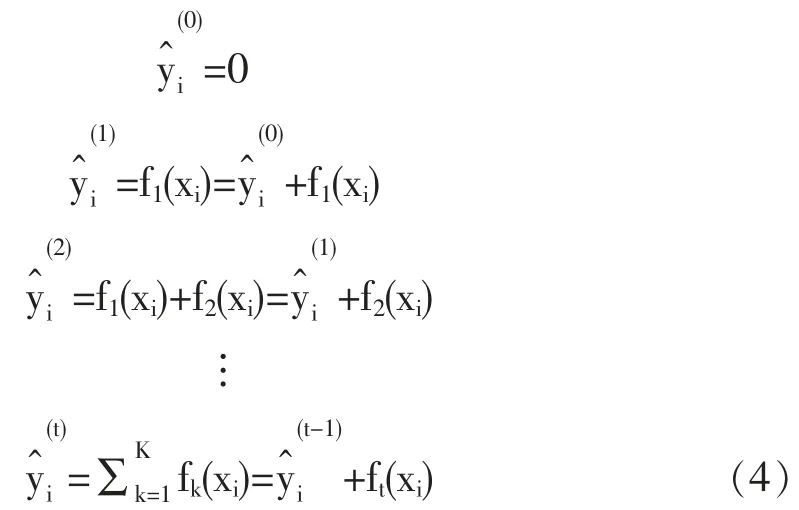
（4）将(4)式代入(2)式可得：

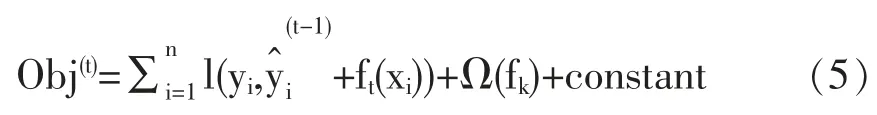
（5）将目标函数进行二阶泰勒展开，并且加入正则项：

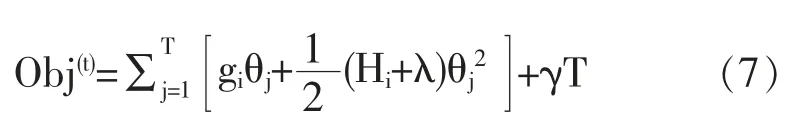
上述(7)式中，θj表示为一个不确定的叶子节点的值。因此Obj(t)（目标函数）对θj求一阶导数便可求出叶子节点j的最优值θ*j，其值如下所示：

将上述(8)式所得θ*j代入目标函数可得Obj(t)的最小值为：

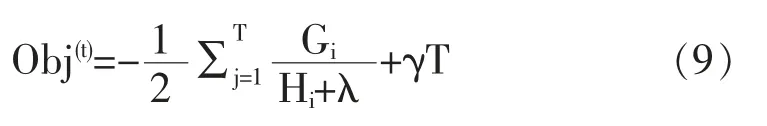
1.2 模型解释

在上述问题模型分析与算法推导的基础上，利用XGBoost算法可以获得预测精度较高的PM2.5浓度预测模型，但该模型与传统的线性模型相比，几乎是一个黑箱模型，针对该问题，本文采用SHAP值对模型中PM2.5浓度的影响因素进行解释分析。SHAP模型在2017年由Lundberg S等提出[21]，可用于提升分类以及回归模型的可解释性。在实际问题中，对于特定的预测样本，预测模型都能得到一个相应的预测值，SHAP value则是该样本中每个特征所获得的数值。

SHAP模型的核心思想,在所有样本中，若第i个样本为xi，第i个样本的第j个特征为xij，特征的边际贡献为mcij，边的权重为wj，f(xij)是样本xij的SHAP值，例如第i个样本的第一个特征的SHAP值计算如下：

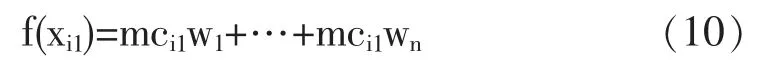
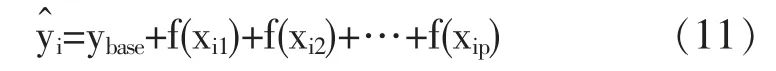
上述（11）式中，f(xij)是样本xij的SHAP值。f(xi,1)是第i个样本中第一个特征对最终预测结果的贡献程度。每个特征的SHAP值则表示的是以该特征为条件时相应模型预测结果的变化。其中，f(xi,1)>0，说明该特征提升了模型的预测值，相反，则说明该特征使得贡献程度降低。XGBoost模型自身的“feature importance”只能体现特征的重要性，但并不能准确地反映该特征是如何影响目标变量的预测结果。而SHAP value的一个最明显的特点是SHAP值能体现每一个样本中的影响因素对预测结果的影响程度，而且还可以说明影响的正负。

1.3 建模流程及模型评价指标

本文对选取的数据指标进行预处理、缺失值填充，具体流程包括各指标数据及目标变量的统计描述、特征变量重要性分析、变量之间的相关性分析。建模流程图如图1所示。

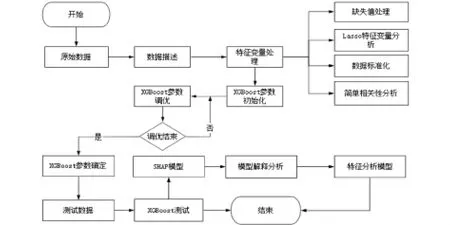
图1 XGBoost与SHAP建模流程图

本文中评价预测模型的指标分别为均方根误差（RMSE）、平均绝对误差（MAE）、拟合程度（R2），其中，模型预测精度高，说明RMSE、MAE的数值越小，R2的数值越大，计算公式如下：

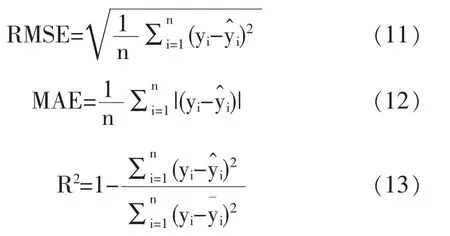
上式中yi表示第i个训练实例PM2.5浓度的真实值，表示第i个训练实例PM2.5浓度的预测值，表示训练实例PM2.5浓度真实值的平均值，n为样本个数。

本文中以XGBoost算法为例，在该算法设定的参 数 中，‘n_estimators、learning_rate、subsample、colsample_bytree、max_depth、tree_method’分 别 表示：迭代次数、学习率、训练模型的子样本占整个样本集合的比例、建立树时对影响因素的随机取样比例、树的最大深度、树的约束算法。算法的核心超参数项的设置情况为：n_estimators=100,learning_rate=0.09,gamma=0,subsample=0.75,colsample_bytree=1,max_depth=7,tree_method=’approx’。

2 数据概括和预处理

2.1 研究区及数据概况

乌鲁木齐作为古丝绸之路的重要通道，位于东经86°37′33”—88°58′24”，北纬42°45′32”—44°08′00”，是典型的干旱区绿洲城市。其东、南、西三面环山，深居我国内陆，海洋气流不易到达。根据2020年中国社会统计年鉴数据显示，2019年乌鲁木齐市PM2.5的年平均浓度为50.0μg·m-3，在31个主要城市PM2.5的年平均浓度排名中位居第24位，同时空气质量等级处于二级的天数排名也相对靠后[22]。目前，乌鲁木齐市在坚决打赢“蓝天保卫战”的号召下，积极践行绿色可持续发展理念，而PM2.5的排放对该地区的环境和人民生活有着重要的影响，因此，进行更为准确的PM2.5浓度预测研究，对城市的绿色发展及干旱内陆城市的可持续发展具有一定的现实意义。PM2.5浓度观测数据及空气污染物数据来源与国家环境在线监测平台（https://www.aqistudy.cn/historydata）公布的全年（2020）逐时监测数据。同时，气象条件随时监测指标：最高气温（℃）、最低气温（℃）等。来源于中国气象数据网（data.cma.cn）。

2.2 缺失值、异常值及目标变量处理

实验过程需要对数据集进行标准化处理。同时，对获得的原始数据集经过整理后发现存在一定的缺失。其中Wind_pow和Tem_low缺失程度最大，其缺失比例达到了0.69%和0.24%。对于缺失特征数据的填充，本实验将数据集分为污染特征因子和气象特征两类，根据气象特征类别的中位数进行填充。最终得到的样本总量为8746，15个特征变量。原始数据集的统计描述结果如表1所示。

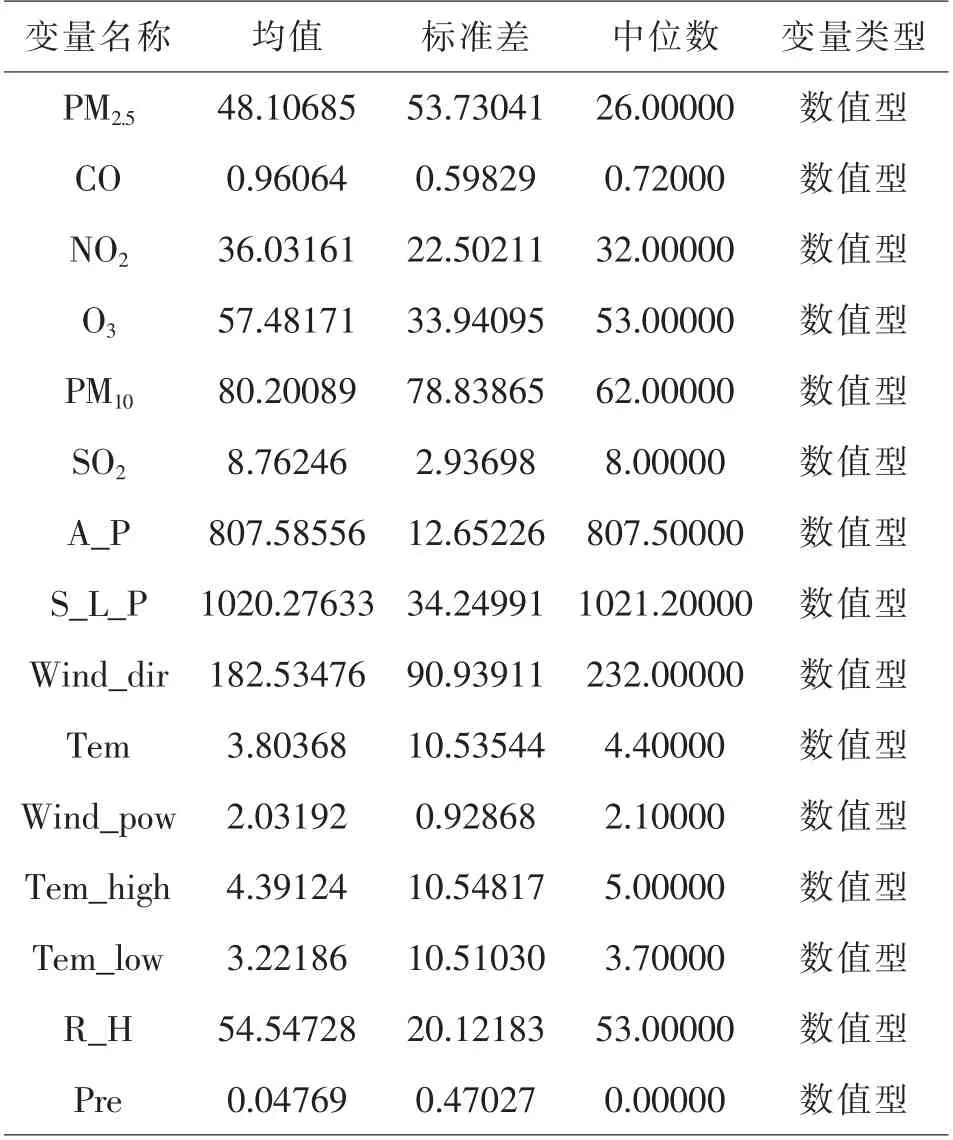
表1 特征变量描述

由表1数据可得：目标变量PM2.5的平均浓度为48.12（μg·m-3），其中，PM2.5浓度的中位数为26.00（μg·m-3），标准差为53.73（μg·m-3）。在目标变量（PM2.5）的统计描述中得到，原始数据集的PM2.5浓度在4.00—360.00（μg·m-3）之间，同时，如图2（a）所示，PM2.5的浓度分布存在严重的右偏，这会显著影响最后的预测结果。因此，本文针对该问题，利用Boxcox变换法来转换PM2.5浓度变量值，以便在平衡的数据集下训练模型。不难发现，变换之后其具有较好的正态分布，如图2（b）所示。

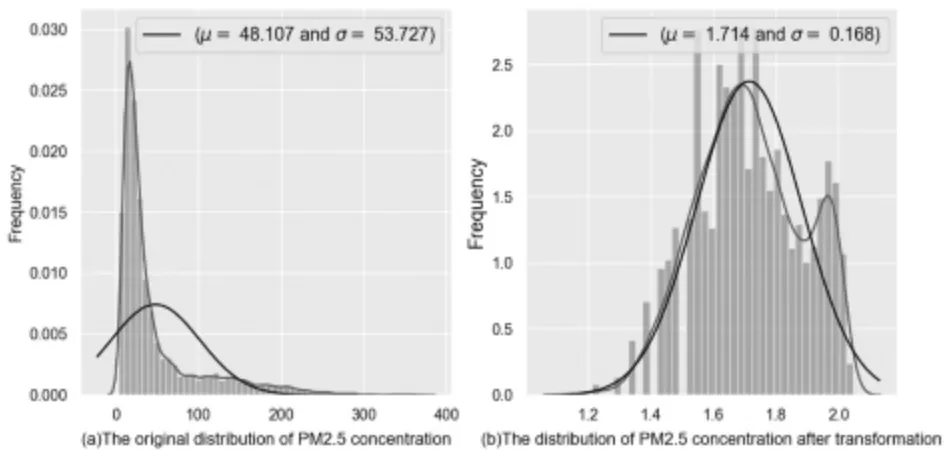
图2 PM2.5浓度分布图

2.3 Lasso特征变量重要性分析

在实际操作中，Lasso的参数值越大，参数的最终目标解个数越少，选出的特征变量数目也越少。本文模型的RMSE值是由交叉验证方法计算所得，然后利用其极小值点来确定最终的参数值。最终的特征变量重要性分布如图3所示。

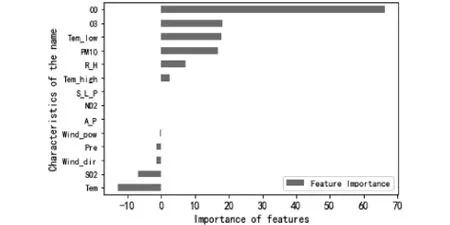
图3 Lasso特征变量重要性分析

3 实验与结果分析

3.1 特征因子分析

3.1.1 污染因子对PM2.5浓度的影响

PM2.5浓度与空气污染物之间存在复杂的转化和传输过程，并且各污染物之间也存在显著的影响。为此，本文进行了研究区域内PM2.5浓度与各变量之间的相关性分析。如图4所示，PM2.5与空气污染因子之间都有一定的相互影响关系。其中PM2.5浓度与CO浓度之间的相互关系最强，与NO2和PM10之间存在一定的正相关，而SO2与PM2.5的相关性较低，所以可以忽略其对PM2.5的影响。

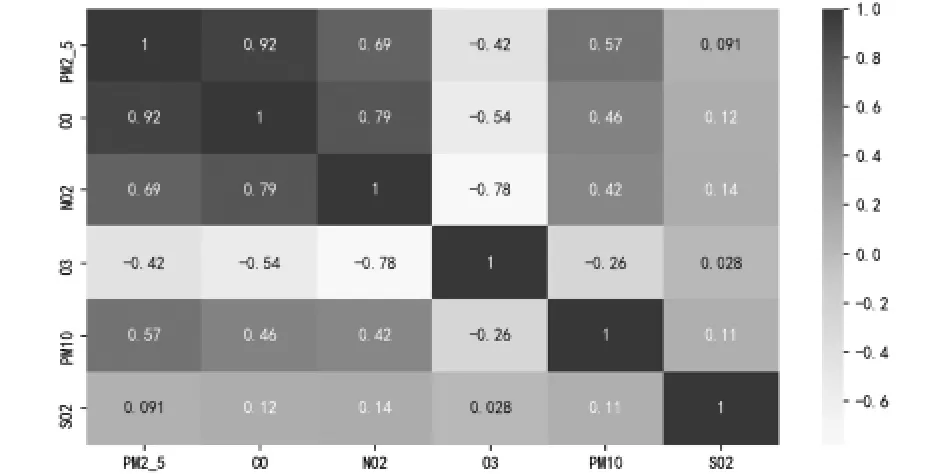
图4 空气污染因子与目标变量（PM2.5）热力图

3.1.2 气象因子对PM2.5浓度的影响

气象因子也是引起空气中PM2.5浓度变化的一个重要因素，如图5 PM2.5浓度与气象因子热力图所示，PM2.5浓度与气象因子之间存在一定的相互影响关系，其中，PM2.5浓度与气温（最高气温、最低气温）存在较强的负相关，与相对湿度、气压和降水量之间从在一定的负相关。

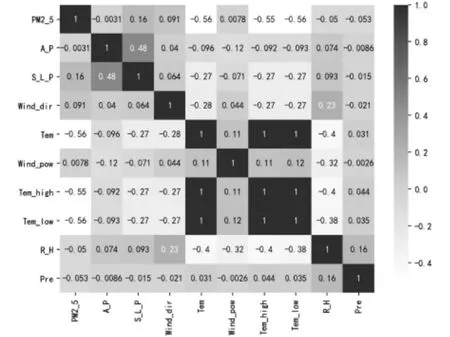
图5 气象因子与目标变量（PM2.5）热力图

3.2 模型预测与对比分析

本文在预测模型性能方面与同类研究进行了对比实验，实验结果如表2所示。由表中的数据可以得出，基于XGBoost算法的RMSE、MAE及R2的值分别为0.205、0.129、0.960，本文算法在各评价指标上都得到了最好的结果，同时该算法在性能方面比LR和BPNN优势显著，主要体现在R2指标上。XGBoost算法能够在评价指标上达到最优的原因在于：一是目标函数中引入了正则项，起到控制和优化预测模型的复杂程度；二是从权衡方差偏差的角度来看，由于其算法降低了模型的方差，使训练的模型更加简单，进而防止模型过拟合的问题；三是该算法采用了梯度提升来获取局部最优解。

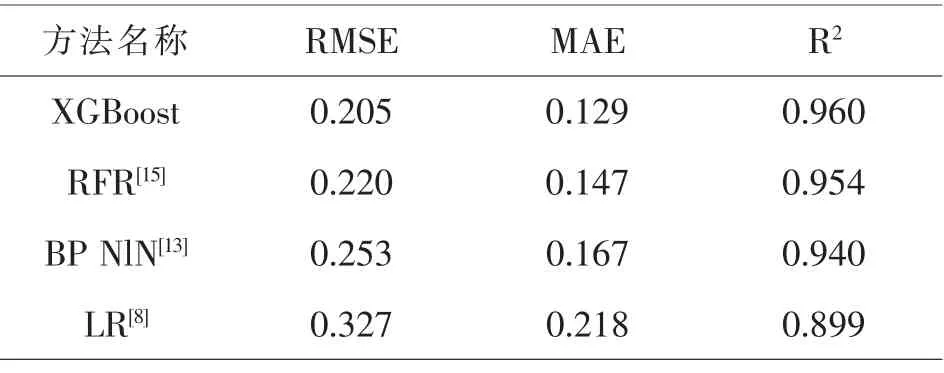
表2 与已有方法的预测性能对比

以XGBoost算法为例，将处理后的数据以70%的数据作为训练数据集，30%的数据作为测试数据集。最终获取的详细结果如表3所示。由表3中的数据可得出结论：XGBoost模型的性能最佳，拟合优度达到0.960，而Adaboost和GBR算法的预测效果相对最差。在R2指标上，XGBoost的值达到0.960，而Adaboost算法的值只有0.913。除了KNeighbor的值能够达到0.956之外，其他两种算法的拟合程度值均在区间[0.910，0.930]之内。

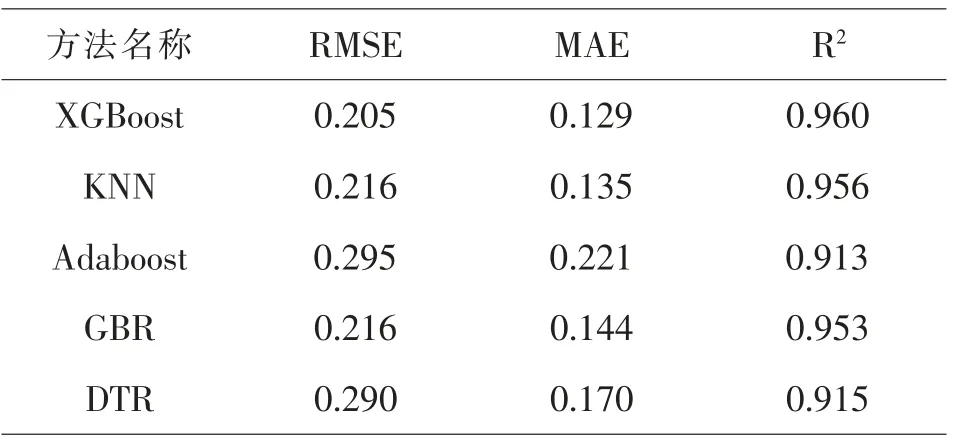
表3 算法预测结果评价指标

综上所述，XGBoost的预测效果最为理想，可以较好地体现PM2.5浓度与影响因素之间的复杂关系。

对比以上算法的预测效果可以看出：（1）在PM2.5浓度预测上，XGBoost算法在各评价指标上均达到最优，这说明本文的指标体系构建是有效的，进一步挖掘PM2.5浓度的波动影响因素，可以更加精确 地预测PM2.5的浓 度。（2）基于 非 线性的XGBoost和RFR预测算法比线性回归、DTR（决策树）以及Adaboost回归预测的效果更加显著，这说明空气中PM2.5数据集往往存在着复杂的非线性关系，并且含有一定程度的非平稳数据，因此基于非线性关系的预测模型可以获得更好的预测效果。（3）XGBoost和RFR算法之所以能够有一个较好的预测效果，是因为它们都是基于集成的方，通过梯度提升的方法去获取局部最优值。研究结果表明，基于XGBoost的预测模型可以较准确的估算区域PM2.5的浓度，并且XGBoost方法在预测模型的泛化与推广能力上具有相对较好的优势。

3.3 预测模型超参数调解及收敛分析

XGBoost中包含有很多超参数，本文实验过程中，利用Grid Search CV方法完成了参数调优，并以R2为最终结果的评价指标。以实验中性能最优的XGBoost预测模型作为训练集，选择了对模型性能影响最大的五个主要参数，参数的搜索区间范围及第一轮参数优化结果如表4所示。

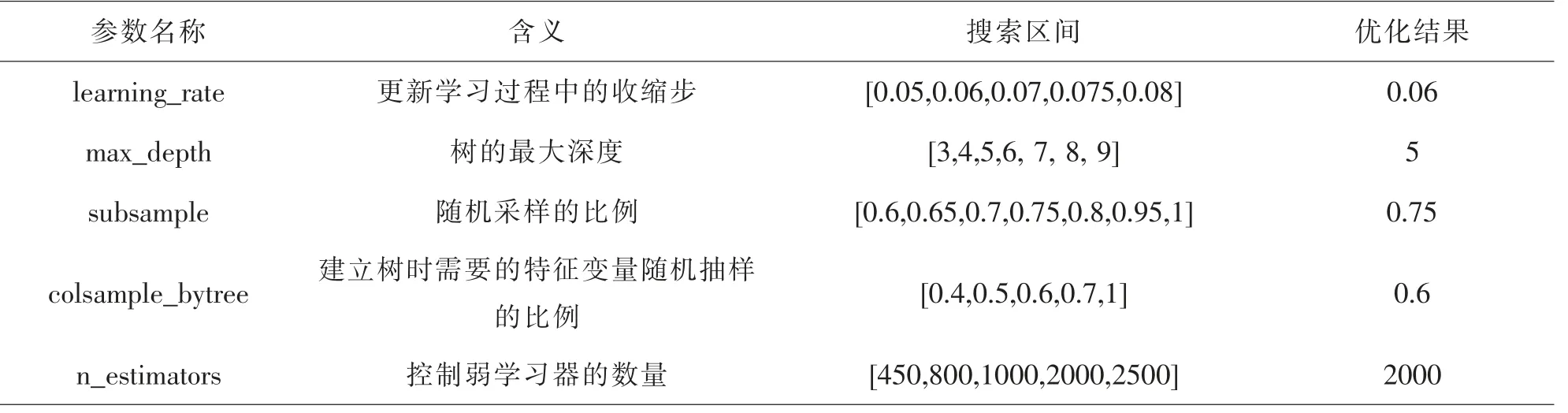
表4 XGBoost模型的参数优化结果

图6(a)-(d)分别表示XGBoost、RFR、BP NN、以及LR的学习曲线。由图6可得各算法的拟合效果相差较大。其中，随着样本个数的增加，预测模型都接近逐步收敛，而XGBoost与RFR的测试数据集和交叉验证数据集在性能方面存在一定的差距，并且对比两个模型发现，当样本数量达到2400时，模型的拟合效果较好。同时，随着样本量的持续增加，交叉验证数据集的性能也逐渐趋向稳定。从模型的拟合趋势来看，当样本数量不断增加时，XGBoost与RFR预测模型的拟合效果也逐渐达到最优。然而，XGBoost在测试集方面的稳健性比RFR更加显著。

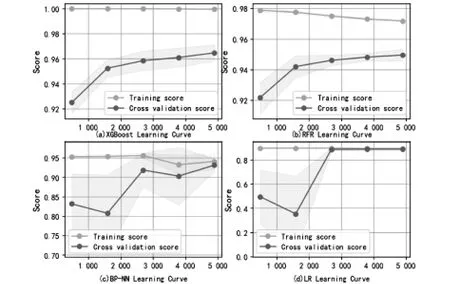
图6 XGBoost与各分类模型的学习曲线对比

3.4 基于SHAP的模型解释分析

SHAP的基本思想是在观察某特定数量样本的预测中，不同的特征变量会对预测结果产生不同程度的影响。图7显示了SHAP的摘要，该图根据选取的各类影响因子对PM2.5浓度的影响重要性进行排序。由图可得，空气污染物中CO、PM10和O3的浓度差异对预测模型的影响较为显著，且均对PM2.5浓度造成正向的影响。即这些特征指标的值越高，SHAP的值越大，对应区域空气中PM2.5的浓度越高。此时就应引起人们的注意，进而采取防护措施。相 反，A_P、Tem、Wind_pow、Wind_dir对其PM2.5的浓度造成了较明显的负面影响，且随着这些指标数值的增大，SHAP的值越小，导致其负面影响程度增加。以风向为例，一定风速的风向将会促进区域空气污染物（PM2.5）的转移，进而使得区域空气污染物中的PM2.5浓度大幅下降。

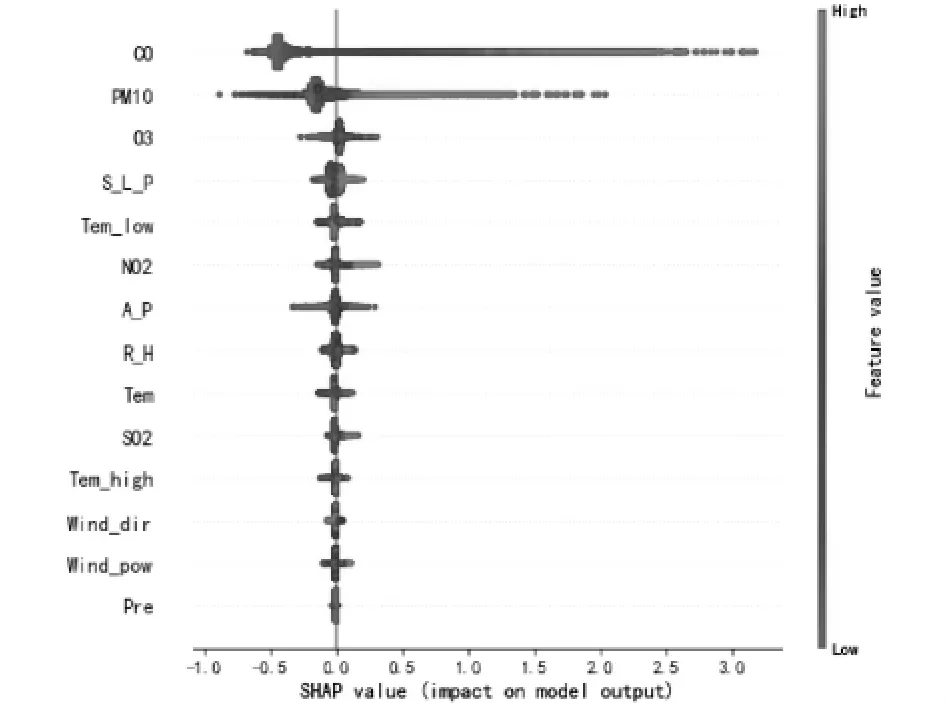
图7 SHAP特征分析

在图8中，通过修改模型中的特定特征变量，在y轴画出特征变量的SHAP值，在x轴画出特征变量的值。在图8(a)中，选取CO浓度作为特征变量来确定Wind_pow从-1.0逐渐增加到1.0时的影响。红色点和蓝色点分别代表Wind_pow较高值点和较低值点。当CO浓度的值较低时，Wind_pow的SHAP值大于0，这表明CO的浓度降低会使区域空气中PM2.5的浓度也随之降低。即在CO浓度和Wind_pow交互影响的情况下，该区域CO浓度的降低会导致其空气中更低的PM2.5浓度。图8(b)显示了Tem和PM10在PM2.5浓度预测模型中的影响。PM10浓度值较低的点（蓝色点）大多位于图的右侧，其值也相对较高。位于左侧（即Tem高和PM10高）的红点可能对应于乌鲁木齐市冬季PM2.5浓度较高时收集的数据。

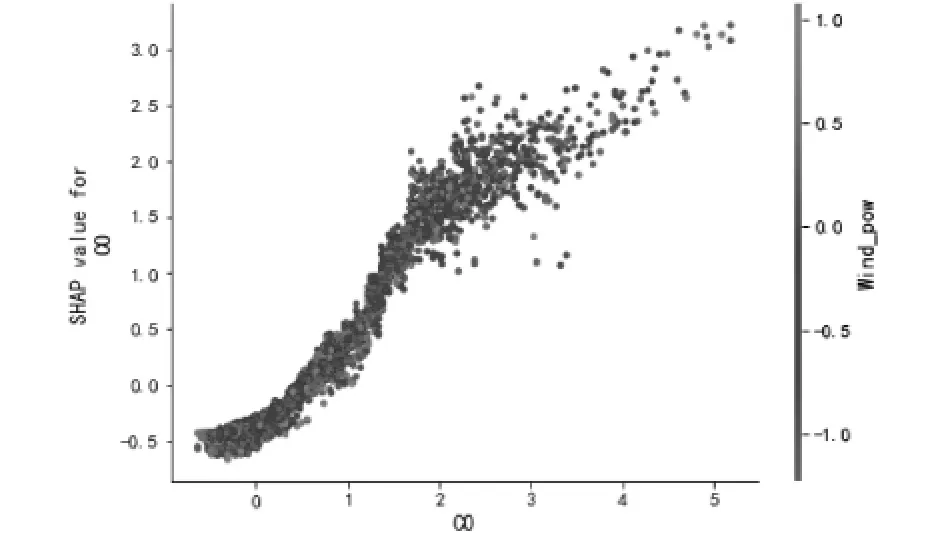
图8 (a)CO和Wind_pow对模型产出的影响

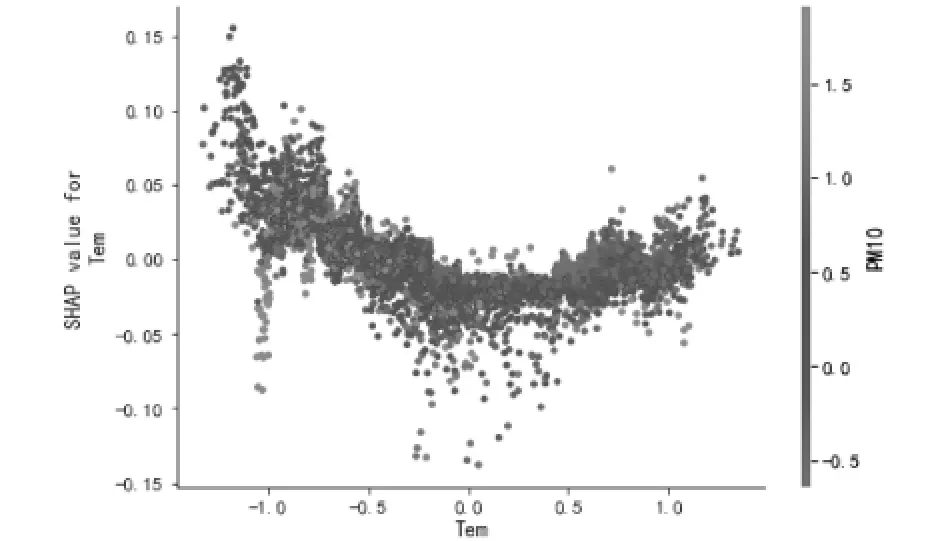
图8 (b)Tem和PM10对模型产出的影响

图9显 示 的 是XGBoost、RFR和SHAP训 练后，3种算法的特征变量重要性对比结果。经过3种算法的模拟训练后，特征变量重要性的排序并不完全相同。由图9可看出影响区域空气中PM2.5浓度的关键因素是CO浓度、PM10浓度、O3浓度以及气温（Tem）。3种算法在进行变量特征重要性排序时都将CO浓度、PM10及O3浓度排在靠前的位置，但在SHAP模型中的CO浓度值最大。

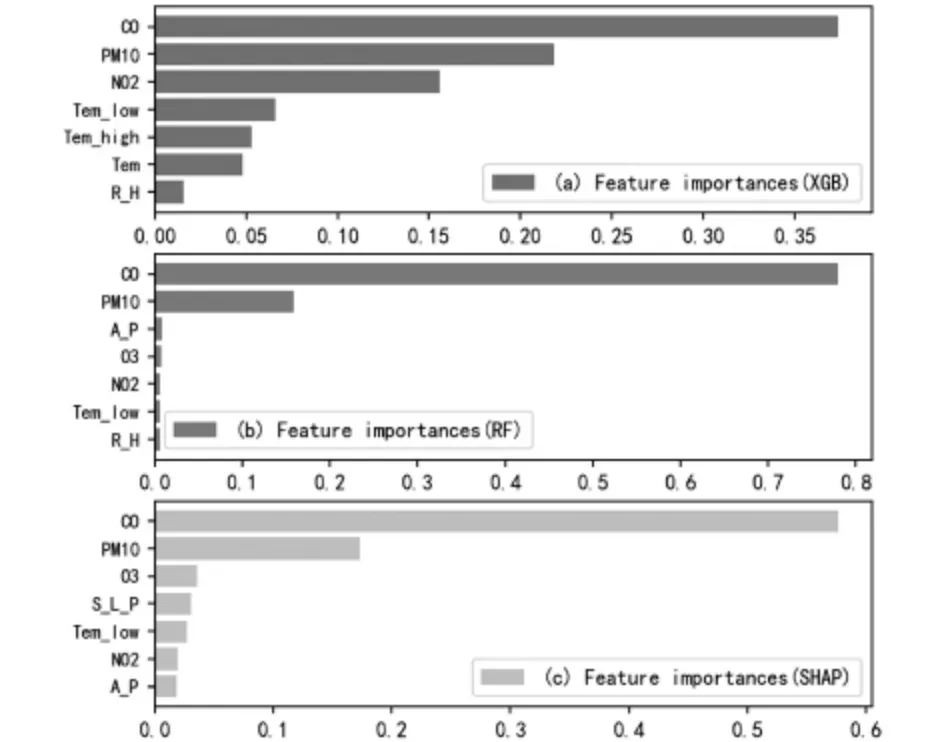
图9 XGBoost,RFR和SHAP特征变量重要性对比

具体而言，区域空气污染物中CO浓度越低，其PM2.5浓度越低是肯定的，这表明CO浓度与PM2.5浓度之间存在着特定的转化关系。图9还可以发现，气象因子（Tem）与PM2.5浓度之间也存在着相互影响的关系，可理解为较高的气温会促进空气污染物之间的相互转化。以上所述的具体转化途径本文不予以讨论，可由后期实验来完善。

4 结论

在工业化和城市化处于快速发展期间，常常会伴随着能源及其他一些资源物质的大幅消耗，致使空气中颗粒物的含量有了明显的增加，这将会对公众的健康和生态文明建设造成巨大的影响。

本文基于XGBoost与SHAP模型以乌鲁木齐市为研究区域，对其空气污染物中的PM2.5浓度进行了预测。（1）将预处理完的特征变量数据作为XGBoost训练模型的输入，然后训练得到了最优的预测模型；并且进行了对比实验，验证了XGBoost模型预测性能的优异性。（2）利用SHAP值对已获得的预测模型特征进行了合理地解释。同时，结合XGBoost、RFR以及SHAP模型的特征变量重要性排序，进一步得到了影响乌鲁木齐市区域空气污染物PM2.5浓度的主要影响因素是CO浓度、PM10浓度、O3浓度以及Tem（气温）。（3）在XGBoost和其他预测模型的学习曲线对比结果中得出，随着样本个数的增加，预测模型都逐渐趋于收敛。当样本数量持续增加时，XGBoost与RFR预测模型的拟合效果也逐渐达到最优的效果，而XGBoost在测试集方面的稳健性相比RFR更加显著。