初中数学教学中学生逻辑计算能力的培养路径
贵州省毕节市七星关区阿市中学 张达敬
在初中数学的基础教育中,对于学生数学逻辑计算能力的培养一直不受广大教师的重视。学生往往忽略准确计算的重要性,导致计算马虎或者因为对于计算规则和逻辑的理解不够透彻而计算错误,造成不可估量的损失,同时也打击了学生的数学学习兴趣。学生的逻辑计算能力又分为计算的基础能力和逻辑计算应用能力,前者是逻辑计算能力的基础,后者是逻辑计算能力的延长和拓展。因此,想要全方位提升学生的逻辑计算能力,需要从基础运算以及逻辑计算应用能力入手,打造层层深入、由浅入深的学习和训练机制,从而提升学生的逻辑计算综合素养。
一、培养良好计算习惯和基础
现阶段的初中数学教学中,教师往往忽视强调学生逻辑计算能力的重要性,导致许多学生在进行计算的过程中马虎了事,计算逻辑不清晰,计算步骤混乱;同时对于计算的过程也十分省略和敷衍,学生在计算的过程中频频出错,从而影响其数学成绩和数学学习的兴趣。
教师在对学生进行良好的计算习惯培养时,应该注重强调学生运算草稿的清晰和明了。一是方便计算时厘清思路;二是如果计算过程中发现错误的地方,也方便及时回头在草稿中查找错误的根源,从而提升学生的计算效率,提高学生的计算基础能力。
例如,教师在对学生进行北师大版教材七年级下册“整式的乘法”一课的教学时,本课的教学目标和主要内容是理解多项式乘法法则,会利用法则进行简单的多项式乘法运算,而其中的教学重难点在于对多项式乘法法则的了解和应用,理解运算法则和其探索过程。因此,对于多项式乘法法则的运用和计算过程在本课教学中显得尤为重要。教师引导学生通过探索出整式乘法(m+b)(a+n)=m(a+n)+b(a+n)=ma+mn+ba+bn的运算规则之后,可以继续引导学生将(m+b)(a+n)中的(a+n)看作一个整体,得出(m+b)(a+n)=m(a+n)+b(a+n)=ma+mn+ba+bn,从而将多项式转化为单项式乘以单项式。教师可以引导学生得出:多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所有的积相加。学生在了解和掌握了多项式相乘的运算规则后,教师出题让学生进行运算练习。比如,请计算以下多项式乘积:(1)(1-x)(0.6-x);(2)(2x+y)(x-y);(3)(x-2y)²;(4)(-2x+5)²。在学生进行以上题目运算时,教师需要进行重点强调的是:用一个多项式的每一项依次去乘另一个多项式的每一项,不要漏乘,在没有合并同类项之前,两个多项式相乘展开后的项数应该是原来两个多项式项数之积。同时,多项式里的每一项都包含前面的符号,两项相乘时先判断积的符号,再写成代数的形式。展开后若有同类项,要合并,化成最简形式。
这些注意事项最多体现在学生的草稿运算上面,需要学生进行工整的草稿书写,并且每一步都要仔细进行求证和转化,从而在多个解题步骤之后得出最终的正确解答。草稿的标准和规范书写不仅有利于学生形成较为清晰的运算思路、提升运算正确率,同时,学生如果通过最终的检验发现运算结果出错,也可以及时返回草稿快速检查自己的解题步骤是从哪一步开始出错的。
通过对学生的运算解题步骤的规范和强化,并且注重学生的草稿运算过程的规范和整理,可以提升学生在规定的运算法则下的基础运算速度,从而打下良好的运算基础,形成良好的运算习惯。
二、学习估算与巧算技巧
对于一项复杂又烦琐的无理数数学运算过程的检验和实际问题的估算与比较,除了回头再重新运算一遍去比对结果,或者运用计算器帮助,同时翻看草稿的运算过程和步骤之外,教师也更应该注重对于学生的估算与巧算的检查能力培养。估算与巧算是指学生根据列出的算式结构和特点,进行计算结果的区间值估计。估算和巧算可以将正确答案的一个区间值依据其算式规律快速得出,从而降低了学生答案的检查步骤和出错风险,同时提升了学生的运算速率和计算正确率,提升了学生的解题信心。
例如,在进行北师大版八年级上册“估算”一章的学习时,教师应该明确估算对于学生进行数学逻辑计算和结果检验的重要性。但由于此阶段的学生对于估算这一概念还比较陌生,在实际的学生估算教学中教师需要通过大量的题和学生实践,并且运用符合生活常识的例子让学生体会估算的方法运用,从而让学生初步形成对于估算的意识,发展学生较为良好的数感。
对于学生估算的教学内容与目标,主要分为估算一个无理数的大致范围,比较两个无理数的大小,会利用估算技巧解决一些简单的实际问题;同时经历实际问题的解决过程和平方根、立方根的估算过程,发展估算意识和数感。
让学生从实际问题的解决和估算中去找到估算的基本运用法则,形成良好的数感,教师需要给出较为贴合实际的情境问题让学生进行数字估计。例如,某市开辟了一块长方形的荒地用来建一个以“环保”为主题的公园。已知这一块地的长是宽的两倍,它的面积为40万平方米。那么,公园的宽是多少?长是多少?学生一开始拿到这样的估算类题目,可能会一筹莫展。教师可以从侧面引导学生用估算的思维进行思考:假设公园的宽有1000米,那么满足题目中给出的条件吗?学生经过思考之后发现不满足,从而会想办法调整对于公园宽度的估算,再次进行验证。在这个过程中,学生就慢慢掌握了实际问题的估算基础思维,从而形成较好的估算能力和数感。

教师让学生之间进行交流,并在适当时机引导学生进行估算思维的思考,在解决问题的同时引导学生对解决方法进行总结,和学生一起归纳出估算的方法,让学生从被动学习转为主动探究,激发学生的学习热情,使其形成良好的估算解题思维。
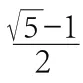
通过这样的比较方法的引导和教学,教师可以帮助学生在分析和简化算式的过程中逐渐形成良好的估算逻辑,并且加强学生数学逻辑计算能力的提升;同时帮助学生更好地运用估算解决实际问题,检验学生的解题过程等,整体提升学生的运算效率和逻辑运算能力。
三、重视逻辑计算的层层递进
学生的逻辑计算思维和能力是一个层层递进的关系,计算题目中的推演逻辑与学生的逻辑计算能力有着密不可分的关系。逻辑计算中的推演和转化往往有着由浅入深、由易到难的知识储备特点。因此,初中的数学逻辑计算能力是一个承上启下的重要过渡阶段。
比如,在北师大版数学九年级上册“一元二次方程”单元的学习中,教材要求从认识一元二次方程,到用配方法求解一元二次方程,再到用公式法求解一元二次方程、用分解因式法求解一元二次方程,通过层层的方法了解和递进,帮助学生在进行方法优化和逻辑推演的过程中更加深入地了解一元二次方程的简化求解过程,从而深化一元二次方程的求解思路和解题思维。同时,又利用一元二次方程的根与系数的关系的探索,深化对一元二次方程的应用,从而深入思考出一元二次方程的实际应用题解题方法。通过这样的层层递进,可以帮助学生更好地理解一元二次方程的逻辑计算基础和思维,做到灵活运用。
(一)配方法的理解和运用
教师首先应该为学生介绍配方法求解一元二次方程的过程和思路,告诉学生配方法是在探索一元二次方程近似解的基础上研究的一种求精确解的方法,是一元二次方程解法的通法。因为用配方法解一元二次方程比较麻烦,一个一元二次方程需配一次方,所以在实际解一元二次方程时,一般不用配方法。但是配方法是导出求根公式的关键,且在以后的学习中也会用到这个方法,因此理解配方法并会运用配方法求解一元二次方程十分必要。教师应该通过引导学生从前面两节课的实例引入求精确解,由于已经能够解形如(x+a)2=b(b≥0)的方程,这时可以直接引入一元二次方程的基础解法——配方法。配方法的关键是正确配方,而要正确配方就必须熟悉完全平方式的特征。因此教师在进行配方法教学时应该注意确保学生会使用开平方法解形如(x-m)2=n(n≥0)的方程,从而帮助学生理解配方法的解法思路和原则。同时教师也应该培养学生会将一元二次方程通过配方法转化为(x-m)2=n(n≥0)的形式,从而让学生学会理解和体会转化的数学思想方法。
(二)公式法的推进
通过对于前几课一元二次方程的初步了解和配方法的学习,学生认识了一元二次方程的一般形式,即ax2+bx+c=0,并且已经能够熟练地将一元二次方程化成它们的一般形式。大部分学生已经能够利用配方法解一元二次方程。然而在配方法基础上,教师需要带领学生了解更加简便的方法,即用公式法求解一元二次方程。
公式法实际上是配方法的一般化和程式化,然后再利用总结出来的公式更加便利地求解一元二次方程。因此,此节的教学目标为学生能够在教师的指导下正确导出一元二次方程的求根公式,并且在探索过程中培养学生的数学建模意识。同时,也要求学生能够根据方程的系数判断出方程的根的情况,从而使学生能够在练习和思考中熟练使用求根公式解一元二次方程,提升学生的综合运算能力。
(三)因式分解法的教学分析
前几册的教学中,学生已经对一元一次方程、一元二次方程组、可化为一元一次方程的分式方程等进行了了解和学习;在八年级时也学习了因式分解,掌握了因式分解法及运用公式法熟练分解因式;本单元中前几课也讲解了配方法和公式法解一元二次方程的步骤以及原理。在这些基础上,教材在用因式分解法解一元二次方程是解决特殊问题的一种简便、特殊的方法的基础上,提出了此次学习任务——能够根据已有的分解因式知识解决形如x(x-a)=0和x2-a2=0的特殊一元二次方程。而这仅仅是教材规定的基础教学目标。数学教学是由一个整体体系出发去安排分支教学的,因此其教学特点应该是由层层递进的课堂组成的。本课因式分解法的内容属于方程与不等式这一数学学习领域,因而能够根据具体的一元二次方程特征,灵活选用方程的解法,让学生学会解决问题的方法多样性和角度多样性,同时会用因式分解法解决某些简单的数字系数的一元二次方程,从而提升学生的数字敏感力和逻辑运算能力。
在本节课堂教学中,教师除了教会学生使用因式分解法解决部分一元二次方程以外,也应该注重对于学生学会使用综合性多元化的解法的能力培养,让学生学会辨别不同的方程式情况,从而选择最为合适的解法快速、高效地解决问题,从而锻炼学生的逻辑运算综合能力,提升学生的解题效率。
在对学生进行逻辑计算的层层递进教学时,教师应该从多角度、多方面进行考量和设计,让学生能够在一个循序渐进、由浅入深的思考和训练环境中逐渐掌握数学逻辑运算的思维和架构,从而做到知识成体系、训练灵活、贴合实际的教学目标保障,从真正意义上高效提升学生的逻辑计算能力和数学综合素养。
总而言之,对于初中学生的逻辑计算能力的培养是一个层层递进、由浅入深的教学过程,是教师根据小学的简单计算知识教学的延伸和推进的教学结果。同时初中的逻辑计算能力作为一个中间过渡点,有着承上启下的关键作用。因此,对于初中逻辑计算能力的培养需要教师遵循整体原则和逐渐推进的连带原则,让学生逐步完成从简单到复杂、从单一运用到综合分析的逻辑计算能力上的过渡,从而真正意义上提升学生的数学逻辑计算能力和学科素养。

