团数为5的零因子图对应的有限交换局部环

刘 琼, 吴明光

(上海电力大学 数理学院, 上海 200090)

零因子图是近年来一个新的研究领域,主要研究环与半群的代数结构、性质与其零因子图的图结构、图性质之间的关联关系。零因子图的概念首先是由BECK I[1]在1988年提出的,后来又有许多数学工作者对这一概念进行了研究和推广[2-8]。本文主要是利用零因子图的团数来研究相应的有限交换局部环(以下简称“有限局部环”)的代数结构与性质。

本文中所用到的关于代数、图论的符号和语言参考文献[9-10]。

1 引理介绍

假设k≥6,可知a2=b2=c2=ac=ab=bc=0。由(a+c)u=0,可知a+c≠b。 同理可证:a+b≠c,b+c≠a。

2 主要结论

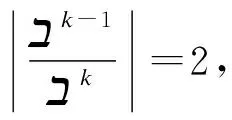
c=(b+d)2=b2+2bd+d2=

b2+d2+2bd=2c+2bd

(1)

下面分情况考虑α12和α22的值。

情况1 若α12=α22,由上面的分析可知,α12和α22不能同时为0。

若α13=α23=c,则b2=(α12)2=α14=cα1=0。这与前面讨论中b2=c相矛盾,故αi3不可能同时为c(i=1,2)。

若α13=α23=a,则b2=(bα1)α2=α13α2=aα2=0。根据类似上述的讨论可知,假设不成立,故αi3不可能同时为a。 同理可证,αi3不可能同时为a+c。

② 若α12=α22=a,下面考虑α1α2的值。

若α1α2=c,则c=aα1=α22α1=α2c=0。这与c不为0相矛盾,故α1α2≠c。同理可证α1α2≠0。

若α1α2=b,则bα1=(α1α2)α1=aα2=0,c=b2=b(α1α2)=0。这与c不为0相矛盾,故α1α2≠b。同理可证,α1α2≠b+c,a+b,a+b+c。

根据上述情况1的讨论可知,情况1的前提假设不成立,故α12≠α22。

① 若α1α2=0,则bα2=α12α2=α1(α1α2)=0,(b+α2)2=b2+2bα2+α22=0。

又因为a(b+α2)=0,这与(1)中的证明相矛盾,故α1α2≠0。同理可证,α1α2≠c。

② 若α1α2=a,则bα2=α1(α1α2)=aα1=c,(b+α2)2=b2+2bα2+α22=c+2c+c=0。与上面的讨论类似,可得出相矛盾。

③ 若α1α2=b, 则bα2=(α1α2)α2=α1α22=α1c=0。与上述的讨论类似,可知假设不成立。由上面的分析可知,α22≠c。同理可证,α22≠0。

3 结 语