突发事件中场域组态异构、边度耦合与舆论圈层扩散的内生影响研究*

阳长征

( 西安交通大学新闻与新媒体学院 西安 710049)

0 引 言

近年来，随着网络媒体的普遍使用，使得危机事件爆发变得越来越频繁，并形成难以遏制的扩散之势。传播学水纹效应模型指出，信息传播过程就像在平静的湖水中扔下一颗石子，水纹就会以很快的速度向周围产生共振波，其扩散的范围和效果受到水质和水面地形的影响而有所不同。而圈层扩散，是指信息在传播过程中，由于传播主体或受体在地域、职业、性别、文化等维度存在相似性或相关性，从而导致该类群体在信息扩散过程中形成圈层化信息行为特征。针对网络突发事件，在水纹传播效应作用下，在事件发生之初，人们由于难以获得突发事件的确切信息，易于产生从众效应，导致信息偏差及认知级联行为的产生，进而形成信息圈层化扩散，从而导致事件演化为群体极化或对事件形成舆论偏差，并影响社会稳定及健康发展。因此，网络突发事件中信息圈层扩散问题已成为网络社会舆情治理关注的重要内容。

1 文献综述

关于信息圈层扩散的影响，国内研究主要集中于三个方面：其一，是对信息圈层扩散的内涵及特征的阐述，如刘明洋等指出社交网络场域中流行语扩散具有明显的圈层性特征，并最终形成圈层话化的舆论环境[1]。周大勇等发现网络空间中信息圈层的形成，其本质是用户的群体组合与分层，从而通过圈层实现信息精准获取。圈层扩散可引起人与媒体形成密切互动，但也会导致用户多重焦虑的产生[2]。其二，是对信息圈层扩散影响因素的探索，如汤景泰等指出信息圈层化程度与用户活跃度间存在关联，同时随着意见领袖涉入信息主题数量的增多，跨越圈层的扩散影响力也随之增大[3]。徐翔针对社交网络信息扩散，发现传者与受者间并非发散式关系，而是呈现传者与受众存在相同或相近的影响力层级，从而形成圈层扩散特征。由此表明，社交网络中信息圈层扩散的产生，会受到网络空间特有的“影响力层级”的影响[4]。其三，是对信息圈层扩散形成机理的探讨，如郑欣等分析了青少年群体中网络语言传播的“圈层”属性及特征类型，并基于社会网络分析角度对线上语言圈层扩散机理进展剖析，提出了青少年社会生活中在线语言圈层化扩散的本质是其社会认同和所形成的生活方式。同时，青少年在线语言的圈层扩散产生了一种跨空间距离的紧密互动及跨时空的集聚[5]。

国外关于信息圈层扩散的相关研究相对较少，而现有的文献主要集中于三方面：其一，部分学者主要围绕圈层扩散的现象及特征进行探索，如Zai等以网络相对完善的高校为研究对象，提出了校园网通信息圈层扩散的关键概念，并指出信息圈层扩散是在大学网络比较成熟及大学生网络行为逐渐流行的条件下所产生[6]。其二，部分学者主要围绕圈层扩散的影响因素及路径进行探索，如Qian等指出随着社交网络的出现和普及，越来越多的用户分享行为形成了圈层扩散特征，如评分、评论和转发等。社交网络该圈层扩散现象产生的因素之一是朋友圈的人际影响力和兴趣，其中兴趣相似性和人际影响力可增强潜在空间中圈层特征的形成[7]。Wu等对信息流进行分析，发现社交圈中的信息流动存在圈层化特征，并且这种圈层间的关联性会随着社交网络中节点属性的相似性的增加而增加[8]。其三，另一部分学者主要从社会文化的角度对信息圈层扩散特征展开研究，如Michaels等人指出信息的圈子交流是一种小组交流的形式，以此可建立关系网络和社区意识，且所有个人及观点都可加入该圈子的交流中，以创建并形成人们共同的信息圈层扩散行为[9]。

总体而言，过去研究主要集中于网络信息圈层扩散的内涵、特征、影响因素及影响机理方面的探讨和分析。然而，组态异构，是指网络空间中特定场域的组成状态及结构的异质化程度。组态异构体现了网络节点间的连接情况及分布的均匀程度，是对节点分布均匀程度的一种度量。组态异构的差异，会对用户在场域中的认知与行为产生影响，高异构易于导致信息行为的离散，低异构则易于导致信息行为的集中，并导致信息形成圈层扩散。同时，边度耦合是指系统中各节点出度或入度的边之间相互依存、相互作用、相互影响的程度，是两个构件相互依赖于对方程度的一个量度。在网络空间中，两个或多个节点的构成，当节点间存在边度耦合时，某个节点的用户或信息发生变化，则能通过其中的边度关系影响到其它节点，从而可将特定节点的信息变化传导至另一节点，并出现相似的变化，该过程则为信息圈层扩散的过程。由此可见，网络空间呈现的组态异构与边度耦合性可对信息的圈层扩散具有重要影响。组态异构与边度耦合两个变量均是根据复杂网络理论及物理学概念进行创新性地合成和提出，而在过去研究中均未有涉及这两个变量的研究文献，也未有关于组态异构、边度耦合与圈层扩散三个变量之间关系的研究。因此，过去尚未涉及组态异构、边度耦合与圈层扩散之间关系的研究，这给本研究在组态异构、边度耦合与圈层扩散之间影响效应的探索留下了空间。

而变量间的内生影响，是指模型体系中的变量存在某种内部关联和作用，且这些变量的变化是由模型体系中的内部参数得以说明，而并非受到模型体系外的因素决定。在一个模型系统中的自变量、因变量均为内生变量，它们之间的内生影响则是由所建构理论模型中的各内生变量间的关系所阐释和说明。同时，过去研究也尚未存在对变量间的脉冲扰动、边际影响及贡献率动态波动等更细致层面的内生影响研究。基于此，本文将组态异构、边度耦合与圈层扩散置于同一理论框架下作为系统结构进行模型建构，采用向量自回归及状态空间模型，分析内生变量间的脉冲响应及边际影响力，并借助面板数据方法分析各变量间影响效应在不同人口统计学群体间的差异性。

2 变量说明与数据收集

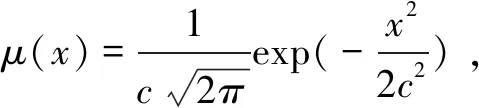
2.2数据收集根据“人民网舆情数据中心”每年度发布的《舆情报告》排行榜单，以其中报告的每年度舆情事件为抽样框，根据《舆情报告》中对事件影响力指数的排名，并同时结合事件知名度、媒体报道程度、危机关注度、危机持续性、危机影响力及危机破坏力等六个维度作为参考标准，梳理和分析我国于2015-2020年所发生的突发事件，最终确定选择11个具有代表性的突发事件作为本研究样本，样本涵盖了卫生、检法、汽车、交通、药品、幼儿、餐饮、医疗、酒店、教育等大多数领域。由于所选突发事件的综合影响力较大，且均为人们日常生活所接触，所涉及的领域均为公众所熟悉并与公众具有较高关联性，公众在事件舆论上的参与程度整体上相对较高，从而可提高数据获取的效率及数据的有效性。其样本分布特征如表1所示。

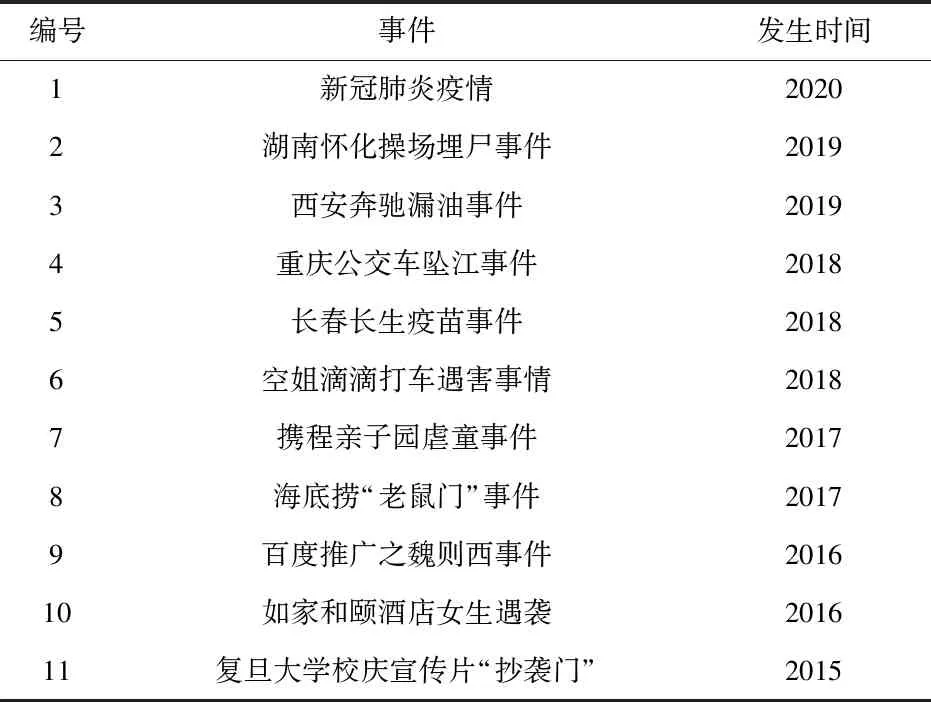
表1 突发事件样本分布特征

本研究使用网络爬虫技术对样本数据进行采集，采用广度优先爬行策略对每个URL指向的页面信息进行抓取，依次反复爬行，直至程序运行结束，以此对网络平台的相关页面信息进行抓取。其数据资料获取主要来源于新浪微博、网易微博、百度贴吧、新浪论坛、搜狐社区、天涯社区、腾讯QQ论坛、猫扑社区等具有较大用户量及活跃度的大型网站、论坛及贴吧。

本研究综合考虑各突发事件样本信息传播过程的有效时长，确定对各样本事件舆情的跟踪时间为21天。经过数据清洗后，整理形成两个数据集，即数据集1和数据集2。数据集1为所采集用户的具体资料信息，主要包含如下变量：用户编号、昵称、所在地、职业、收入、性别、创建时间、认证状态。数据集2为所采集用户的转发及内容、评论及内容、信息时间距离等数据资料，主要包含如下变量：用户编号、是否转发、是否评论、评论内容、总度数、出度数、入度数、中心度、初始语义值、滞后语义值、集聚系数、情感系数、耦合度、边度相关系数等。由于圈层扩散受到传播主体或受体在地域、职业、性别等维度相似性或相关性的影响，因而在数据集1中选取了包含用户所在地、职业、性别等变量，其目的是通过用户所在地、职业、性别等变量对数据集2中的相关变量进行聚类、筛选和整合，以反映本研究中关于“圈层”概念所涉及的地域、职业、性别等多要素特征。在数据集2中，其中用户编号、是否转发、是否评论、评论内容等变量主要采用广度优先爬行方法直接获取，而总度数、出度数、入度数、中心度、初始语义值、滞后语义值、集聚系数、情感系数、耦合度、边度相关系数等变量主要采用复杂网络分析方法直接获取。最后，使用数据集2中的各相关变量的数值，通过“3.1变量说明”中关于圈层扩散、边度耦合及组态异构各变量测量对应的算式计算形成各样本事件的圈层扩散系数(circle)、边度耦合系数(couple)与组态异构系数(hetero)三个变量对应的时间序列，以及包含各截面样本的面板大数据。

3 模型构建

向量自回归模型(VAR)是用以对多维时间序列中的一变量对另一变量动态影响分析的一种时滞性方法，是以每个变量的滞后项作为其他变量函数的自变量来建立模型，从而实现对变量间的相互扰动分析。VAR通常将所有变量视为先验内生变量，它弥补了联立方程模型存在的缺陷，即联立方程模型中某些变量的外生性假设具有临时性，通常没有得到较为成熟理论的支持。而VAR中一组变量的当前值由所涉及变量的过去值来解释，它描述了所涉及变量的内生联合机制。因此，由于本文研究的内容为突发事件中场域组态异构、边度耦合与舆论圈层扩散的内生影响，且变量间的影响存在时滞性，即一组变量的当前值需由所涉及变量的过去值加以解释，故适合选择VAR模型对各内生变量关系进行分析，同时也可避免采用联立方程模型存在的不足。

对VAR模型进行统计分析和时滞长度判断，根据LR检验，以及FPE、AIC、SC、HQ信息准则最小化的标准，对应的统计结果显示，VAR模型的最佳时间滞后长度为2期。在此基础上，对VAR模型进行设定和估计。其对应的模型形式如下：

其中，circle为圈层扩散，couple为边度耦合，hetero为组态异构，t为时间节点，εi为随机误差项。

以内生变量滞后2阶建构VAR模型，并对其进行模型估计，其结果显示，VAR模型的三个方程中各项系数显著性检验的|t|值均大于0.05显著水平对应的临界值1.96。同时，可决系数R-squared值均较大，表明所构建的VAR模型与样本数据拟合度良好，该估计结果可用于组态异构、边度耦合及圈层扩散之间动态影响的相关分析。

4 脉冲响应及波动分解

4.1脉冲响应分析脉冲响应函数(IRF)是用于解开VAR模型中变量之间关系的工具，它是一个变量在受到其它内生变量短暂冲击影响时而出现的结果。IRF可用以分析VAR模型中各变量间受到外界冲击时，其它内生变量对该冲击所作出的响应情况，包括响应的大小、响应滞后长度、响应的动态过程等内容。

为了揭示组态异构、边度耦合及圈层扩散之间的动态扰动特征，在VAR模型估计基础上分别对组态异构、边度耦合及圈层扩散进行脉冲响应分析。此处采用因子的逆来正交化进行估计，对应分析结果如图1所示。

在图1中，在第一行脉冲图中，突发事件舆论场域组态异构自相关效应的冲击迅速传导至组态异构自身，舆论场域边度耦合及圈层扩散的冲击于滞后一期开始产生影响。其中，舆论场域组态异构的自相关滞后影响效应较大，边度耦合冲击及圈层扩散的冲击效应较小。在第二行脉冲图中，突发事件舆论场域边度耦合的自相关滞后效应及组态异构的冲击对边度耦合迅速产生影响。其中，组态异构冲击的影响较大、时间较长，边度耦合自相关效应的影响较大、时间较短。在第三行脉冲图中，突发事件舆论场域边度耦合冲击及圈层扩散自相关效应均迅速对圈层扩散产生影响。其中，舆论场域圈层扩散自相关效应、边度耦合及组态异质的冲击影响均较大，舆论场域圈层扩散自相关效应与边度耦合具有断尾效应，组态异构具有长尾效应。

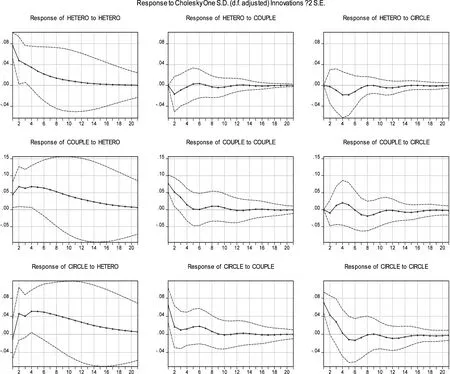
图1 脉冲响应分析

针对其中断尾效应与长尾效应，出现该结果可能的原因在于：一方面，在突发事件网络中，由舆论场域的圈层扩散和网络边度耦合两因素引起的滞后相关强度较弱，且持续时间较短。同时，由于人们在突发事件中，由圈层扩散自相关效应与边度耦合形成的群体性信息分享及通过邻近用户节点进行信息分享的意愿也较弱。而由舆论场域中组态异构引起的用户特征及认知的差异则导致了分散性观点，从而成为人们对突发事件持续关注和扩散的关键动力因素。另一方面，该断尾效应与长尾效应的产生，是由于突发事件舆论场域中信息圈层扩散在网络传播中存在“沉默螺旋”现象，通过场域组态异构性维度在用户同质化和异质化两头差异性分布，使得突发事件舆论中的优势群体在观点表达时呈现不断增强趋势，而事件舆论中的弱势群体在观点表达时则不断减弱，从而导致突发事件舆论场域信息圈层扩散自相关效应与边度耦合存在断尾，组态异构存在长尾。

关于突发事件舆论场域中组态异构与边度耦合对信息圈层扩散存在显著脉冲滞后影响，产生该结果可能的原因在于：级联理论指出，信息级联发生于个体观察到他人的行为，而忽视自身所获得的信息而就选择跟随他人的行为，它可解释行为的局部一致性和群体性行为。针对突发事件舆论，场域中组态异构性与边度耦合性可引起舆论场域出现差异化的用户相似度。然而，当所参照的群体与用户自身在某些维度上存在相似或趋同时，该群体的信息行为便可引起个体的级联和跟从。同时，社会学理论指出，差序格局作为社会关系结构现象，常发生于熟人关系、地缘关系中，其中信息的传播以个体为中心，像水波纹一样推及开去。在该差序格局中，每个人均以自我为中心结成网络，就像将一块石头扔至湖中，以这块“石头”(即个人)为中心点，在四周形成一圈圈波纹，波纹的远近可以标示社会关系的亲疏，并随自身所处时空的变化而产生不同的圈子。因此，针对突发事件，不同的场域组态异构与边度耦合形成了不同程度的用户相似性，从而产生差异性信息级联行为，加之受到用户相似性所引起的差序格局的影响，进而形成了差异性的信息圈层扩散效应。

4.2波动贡献率分解方差分解作为VAR模型中的重要组成部分，是用于分析VAR模型中相关内生变量的冲击对特定内生变量变化贡献率的一种方法。一旦拟合了VAR模型，则需使用方差分解来帮助解释。 分解的方差则是每个变量贡献给其它变量的信息量，它估计了每个变量的误差方差有多少可以由其它变量的外来冲击所解释。

为了比较组态异构、边度耦合及圈层扩散相互扰动效应的大小，从而识别出不同影响因素对组态异构、边度耦合及圈层扩散影响的重要程度，需在上述各影响因素动态扰动特征分析的基础上，分别对各因素的波动贡献率进行方差分解。其方差分解结果如图2所示。

图2 方差分解分析

由图2可见，在突发事件舆论场域圈层扩散方差分解中，对于突发事件整个舆论演化过程，边度耦合对圈层扩散波动的贡献率最小，约为18%；圈层扩散自相关贡献率较大，约为22%；而组态异构最大，约为60%。突发事件中，舆论场域组态异构对边度耦合波动的贡献率最大，占比约为78%；边度耦合自相关效应较大，约为20%；圈层扩散最小，约为2%。突发事件中，舆论场域组态异构自相关效应对组态异构波动的贡献率最大，占比约为90%；边度耦合最小，约为3%；圈层扩散影响效应较大，约为7%。

针对上述方差贡献率差异，表明突发事件舆论场域中的圈层扩散自相关效应与边度耦合对突发事件场域信息圈层扩散影响的滞后性较弱，组态异构对突发事件舆论场域信息圈层扩散影响的滞后性较强。产生该结果可能的原因在于：突发事件中，舆论场域的圈层扩散和网络边度耦合所具有的自相关性较弱，且持续时间较短，从而人们在突发事件中由圈层扩散自相关效应与边度耦合形成的群体性信息分享及通过邻近用户节点进行信息分享的意愿也较弱。突发事件中，由舆论场域组态异构引起的用户特征及认知差异，导致了分散性观点，则成为了人们对突发事件持续关注和扩散的关键动力因素。基于上述原因，从而出现了突发事件舆论场域组态异构与边度耦合对舆论场域信息圈层扩散的波动贡献率存在差异。

5 影响力及群组分析

状态空间模型(SSM)是一类动态时域模型，是用以分析系统中各自变量每一单位数值对因变量的影响效应大小，即在某一时间内自变量对因变量产生的边际影响力的动态变化过程。SSM相对于其他边际影响分析方法具有较大优势，即SSM运算方法的核心是Kalman滤波，Kalman滤波针对时间节点t可基于所有可获取的信息实现对拟合状态向量进行最理想迭代。此外，Kalman滤波还可借助预测误差分解拟合似然函数，以此实现对模型的全部未知变量进行运算，且一旦获得新的观察数值，还可借助Kalman滤波持续对状态向量进行拟合和修正。由于本研究对边际影响力的分析需针对时间节点t对状态向量进行拟合迭代，且模型中具有未知变量。因此，本研究适合选用SSM对本研究变量间边际影响力进行分析，可基于所有可获取的信息实现对状态向量的最理想迭代过程，且可借助Kalman滤波持续对状态向量进行拟合和修正。

5.1边际影响力为了进一步了解组态异构、边度耦合及圈层扩散之间的边际影响力，在此使用状态空间模型对各变量之间边际影响力的变化过程进行分析，从而揭示组态异构、边度耦合及圈层扩散之间影响效应的波动过程特征。其对应的模型形式如下：

测量方程：

状态方程：

其分析结果如图3～5所示。

图3结果显示，突发事件舆论场域组态异构对圈层扩散的边际影响力变化均呈倒U型特征，且在第六期至第十四期影响较大。突发事件舆论场域边度耦合对圈层扩散的边际影响力较平稳，呈水平直线特征，且数值较大。

图3 圈层扩散边际影响分析

图4结果显示，突发事件舆论场域组态异构对边度耦合的边际影响力变化均呈倒U型特征，且在第六期至第十五期影响较大。突发事件舆论场域圈层扩散对边度耦合的边际影响力较平稳，呈水平直线特征，且数值较大。

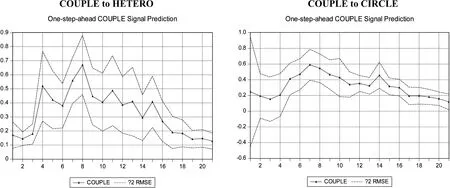
图4 边度耦合边际影响分析

图5结果显示，突发事件舆论场域边度耦合对组态异构的边际影响力变化均呈阶梯型下降特征，且在第二期至第十二期影响较大。突发事件舆论场域圈层扩散对组态异构的边际影响力较平稳，呈水平直线特征，且数值较大。

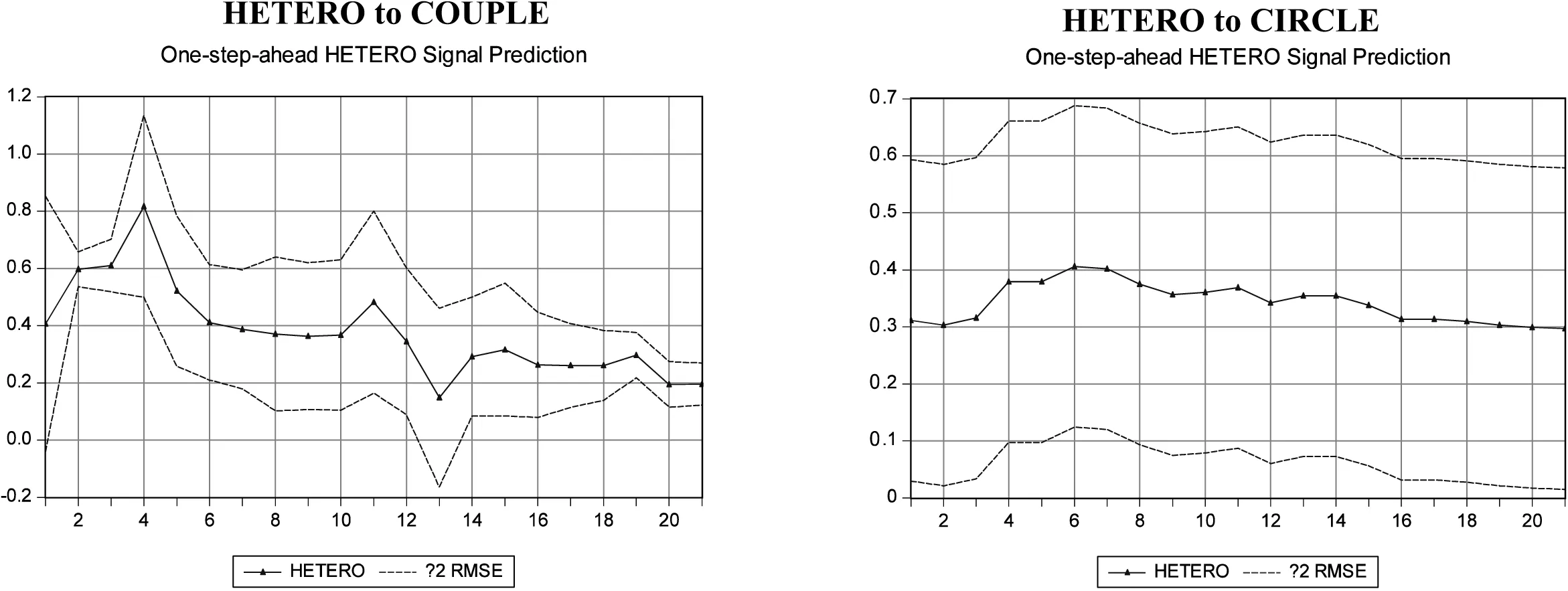
图5 组态异构边际影响分析

关于突发事件舆论场域组态异构与边度耦合对场域信息圈层扩散间的边际影响力呈现倒U形抛物线特征，即突发事件舆论场域中，当对应的边际影响力达到一定数值后则呈递减特征。出现该结果可能的原因在于：经济学效用理论指出，效用是指人们从消费某种商品或服务中获得的满意度或满足感，边际效用则是人们对该商品或服务每增加一单位消费所带来的效用变化，即因消耗一个额外单位商品或服务的行为而带来的效用增量。边际效用递减规律强调，当人们对商品或服务的消费达到某一数值时，商品或服务的边际效用随所消费的商品或服务的增加而减少。针对突发事件，公众在舆论场域中的信息圈层扩散行为，可视为经济行为学中人们对突发事件信息这类特殊商品或服务的消费过程(即信息获取、认知及分享等)。在该信息消费过程中，人们通过突发事件舆论场域组态异构与边度耦合方式对信息进行圈层扩散的行为则满足边际效用递减规律。因此，在突发事件中，人们通过舆论场域组态异构与边度耦合方式对信息圈层扩散的边际影响力，随着时间的推移，当该信息消费行为增长到某临界点时，其边际影响力则达到最大值，其后随着对信息消费的持续增加，其边际影响力则会逐渐减小，即呈现倒U形抛物线特征。

5.2群组分析由于各类用户群体在社会角色及认知心理上的差异，从而导致不同性别、年龄及学历的群体在组态异构、边度耦合及圈层扩散之间的影响效应上存在差异。因此，为了探索不同用户群体间的差异性，采用面板数据模型对数据进行拟合和分析，对应模型为：

其拟合结果显示，对于突发事件舆论场域圈层扩散方程，根据各变量系数大小，通过比较突发事件舆论场域边度耦合变量的系数β1值及组态异构变量系数γ1值，结果显示：突发事件舆论场域中，在性别群组上，女性大于男性；在年龄群组上，29岁及以下群组最大，30～49岁群组较大，50岁及以上群组最小；在学历群组上，小学及以下群组最大，中学群组较大，大学及以上群组最小。

在突发事件舆论场域边度耦合方程中，对于舆论场域组态异构变量系数β3值，结果显示：突出事件舆论场域中，在性别群组上，女性大于男性；在年龄群组上，29岁及以下群组最大，30～49岁群组较大，50岁及以上群组最小；在学历群组上，小学及以下群组最大，中学群组较大，大学及以上群组最小。对于突发事件舆论场域圈层扩散变量系数γ3值，在性别群组上，男性大于女性；在年龄群组上，50岁及以上群组最大，30～49岁群组较大，29岁及以下群组最小；在学历群组上，大学及以上群组最大，中学群组较大，小学及以下群组最大。

6 稳健性分析

本文从替换估计方法方面考虑模型估计结果的稳健性，在VAR模型脉冲响应分析时，之前采用了残差协方差矩阵的Cholesky因子的逆来正交化脉冲，现采用广义脉冲方法替代，即构建一个不依赖于VAR模型中变量次序的正交化的残差矩阵。

在状态空间模型中，之前采用Marquardt进行估计，现采用BHHH算法替代，使用从上次迭代获得的参数拟合值来运算多元变量模型的残差项BHHH的方差与协方差矩阵。

根据稳健性分析结果，采用上述替代方法进行模型拟合，不同方法模型拟合的各路径系数p值均小于0.05的显著水平，以及系数差异性p值均大于0.05的显著水平，检验结果显示采用替代方法估计后的各模型参数值在逻辑关系和逻辑结构上与初始所采用的指标建构的模型分析结果一致，表明上述建构的理论模型及分析结果具有良好的稳健性。

7 结论与启示

通过2015-2020年发生的具有代表性的11个突发事件面板大数据，探索了组态异构、边度耦合及圈层扩散之间动态影响，得出如下研究结论：

a.突发事件舆论场域中，当舆论场域组态异构、边度耦合及圈层扩散受到一个正向冲击时，圈层扩散自相关效应、边度耦合及组态异构的冲击对圈层扩散的影响均较大，圈层扩散自相关效应与边度耦合冲击效应均具有断尾效应，组态异构具有长尾效应。突发事件中，舆论场域组态异构自相关效应的冲击迅速传导至组态异构自身，且影响效应较大，边度耦合冲击及圈层扩散的冲击效应较小。舆论场域组态异构冲击对边度耦合的影响较大、时间较长，边度耦合自相关效应的影响较大、时间较短。

b.突发事件舆论场域中，对于整个舆论演化过程，舆论场域组态异构对圈层扩散波动的贡献率最大，圈层扩散自相关及边度耦合的贡献率较大。突发事件中，舆论场域组态异构对边度耦合波动的贡献率最大，边度耦合自相关效应较大，圈层扩散较小。突发事件中，舆论场域组态异构自相关效应对组态异构波动的贡献率最大，边度耦合及圈层扩散影响效应较小。

c.突发事件中，舆论场域组态异构对圈层扩散的边际影响力变化呈倒U型特征，边度耦合对圈层扩散的边际影响力较平稳，且数值均较大。突发事件中，舆论场域组态异构对边度耦合的边际影响力变化呈倒U型特征，圈层扩散对边度耦合的边际影响力较平稳，且数值均较大。突发事件中，舆论场域边度耦合对组态异构的边际影响力变化呈阶梯型下降特征，圈层扩散对组态异构的边际影响力较平稳，且数值均较大。

d.突发事件舆论场域边度耦合对圈层扩散的影响效应大于组态异构的影响效应，边度耦合对组态异构的影响效应大于圈层扩散的影响效应，组态异构对边度耦合的影响效应大于圈层扩散的影响效应。突发事件中，舆论场域边度耦合及组态异构对圈层扩散的影响效应存在显著差异，在性别群组上，女性大于男性；在年龄群组上，29岁及以下群组最大，30～49岁群组较大，50岁及以上群组最小；在学历群组上，小学及以下群组最大，中学群组较大，大学及以上群组最小。

该研究结论对突发事件网络舆情治理具有启示意义。首先，由于较小的组态异构易于形成群体成员的从众效应，进而产生圈层扩散。同时，当用户具有从众心理时，该群体中的信息集中度则越大、离散程度则越低，则更易于出现边度耦合现象。而边度耦合体现了网络空间中的信息有序性较高、混乱性较低，从而用户在对突发事件信息认知过程中易于产生信息圈层扩散特征。因此，在舆情治理及舆论偏差纠正过程中，应加强对网络场域组态异构及边度耦合指标的监控，通过增加网络信息场域的组态异构以降低用户对突发事件信息圈层扩散效应的产生，以及通过降低网络空间的边度耦合以降低信息圈层扩散效应的产生，从而减小因圈层效应而引起舆论偏差的产生和扩散。其次，由于组态异构、边度耦合及圈层扩散间的影响效应在不同人口统计学群体中存在差异。因此，在突发事件中，对网络舆情治理可采取受众细分策略，根据不同用户群体有针对性地采用不同的监控和管理策略，以提高舆情治理的效果和效率。