质子导体固体氧化物燃料电池模拟研究的进展

＊邱瑞铭 刘建平

（广东工业大学智慧能源研究中心 广东 510006）

前言

煤、石油、天然气等化石能源是当今社会的能源消耗主体，随着消费总量的不断提高，正面临储量减少，开采难度加大，生产成本上升的困境。而世界上日渐突出的能源短缺问题和全球气候变暖的加重，使人们越来越重视能源和环境问题，清洁能源的开发和利用已经成为全球各国发展的重要方向。氢能，是公认的清洁能源，被誉为21世纪最具发展前景的二次能源，它有助于解决能源危机、全球变暖以及环境污染，其开发利用得到了世界范围内的高度关注。目前，世界许多国家都将氢能作为战略性能源来发展，由于其具有零污染、高效率、来源丰富、用途广泛等优势，越来越受到人们的重视。

氢是宇宙中最丰富的元素。氢能是氢的化学能，是氢在物理与化学变化过程中释放的能量。氢在地球上主要以化合态的形式出现，是宇宙中分布最广泛的物质。氢能主要以氢气的形态得到利用。氢气作为二次能源，是最佳碳中和能源载体，可用于发电、发热、交通燃料，具有零污染、热值高、可存储、应用广等优点。氢的储能属性使其具备跨时间和空间灵活应用的潜力，能与可再生能源有效衔接，助力可再生能源消纳与更大规模发展。正是基于氢的优点与潜能，在应对气候变化、全球能源转型的大背景下，国际上普遍认为氢能将成为未来能源系统的关键节点，在全球能源转型及提高能源系统灵活性方面发挥关键作用。

燃料电池（Fuel Cells，FC）是直接将燃料与氧化剂中的化学能转化为电能的发电装置，而质子导体固体氧化物燃料电池（Proton-conducting Solid Oxide Fuel Cells，HSOFCs）因具有不在阳极产生水蒸气和电解质具有较低的传导离子活化能的特点，相比于其他的燃料电池具有更高的平衡电动势和在中温（500℃～700℃）的工作特性。对电池进行建模研究有利于理解电池内部的电化学反应过程和物质迁移过程，对实验研究和提升电池性能有重要的指导作用。

1.H-SOFCs工作原理

在1981年，Iwahara发现SrCeO3基的钙钛矿材料在高温及含氢的环境中展示出质子导电的现象，继而可以将其应用到氢燃料的电池中。随后，开始了H-SOFCs的实验研究。

H-SOFCs的工作原理如图1所示，单电池系统由阴极、电解质和阳极组成。工作时往阴极通入O2，往阳极通入H2。H2在阳极被催化分解成H+和e-，H+通过电解质迁移到阴极形成内电路，而e-通过外电路提供电能；阴极中的O2与H+结合生成H2O。基本工作原理为：

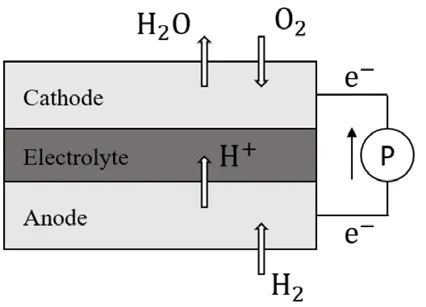
图1 H-SOFCs工作原理

2.电化学模型研究现状

(1)平衡电压的计算

最近十几年，为了探究H-SOFCs的内部的电化学反应和物质迁移，开始对H-SOFCs进行建模研究。目前使用最广泛的为考虑各种极化过电势的输出电压模型，如图2所示：

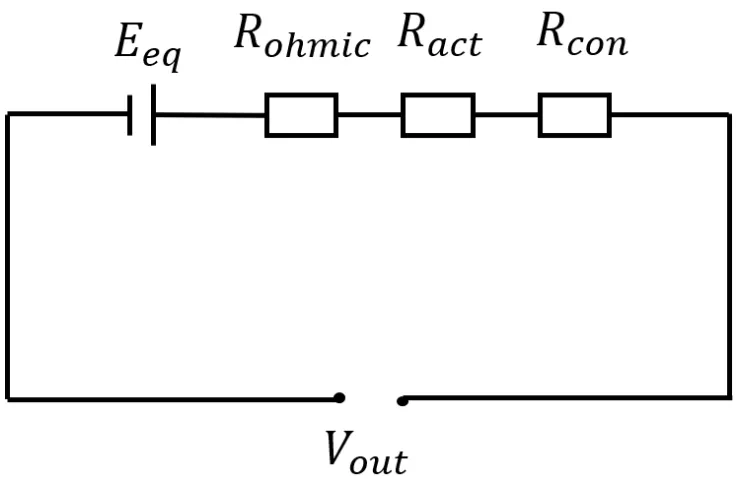
图2 H-SOFCs等效电路图

其中，Eeq为平衡电压；ηohmic为欧姆过电势；ηact为活化过电势；ηconc为浓差过电势。Ni等人建立了早期的H-SOFCs电化学模型，对比发现欧姆过电势是能量损失的主要来源。Patcharavorachot等人在计算浓差过电势时使用具有显式解析表达式的Fick模型，简化了气体在多孔电极中的运输。研究结果表明，H-SOFCs最佳的支撑结构为阳极支撑。这是因为阳极易于传输氢气，而阴极中的水蒸气和氧气扩散缓慢，较厚的阴极将会造成较高的浓差极化损失。除了氢气可作为H-SOFCs的燃料，乙醇、氨和甲烷等也可作为燃料，它们在阳极内部的重整反应为：

为了研究非氢燃料在阳极的重整过程，Menon等人基于阳极的热催化化学作用，建立了一个研究直接内部重整H-SOFCs的计算模型。研究表明，在燃料通道上，较高的入口速度会导致较高的电流密度和功率密度，但会降低燃料的利用率和效率。Liu等人建立的模型用于模拟最佳电极流道参数和最高功率密度，模拟结果表明选择较小的总宽和较小的流道肋/墙与总宽比值，有利于获得较高的功率密度。在实际应用方面，质子导体固体氧化物燃料电池系统与其他热力系统结合可以实现热电联产。

早期模型假设H-SOFCs的电解质材料是纯质子导体，可以用传统的Nernst方程计算平衡电压：

其中，E0是标准电势；R为理想气体常数；T为温度；F为法拉第常数；P为气体分压力。经研究表明，常用的质子导体电解质材料如BaZr0.8Y0.2O3-δ（BZY）在高温和氧化气氛下是混合离子导体，因此在混合离子导体电解质的燃料电池中，平衡电压计算公式为：

其中，tH+和tO2-分别是质子和氧离子的迁移数；PIH2和PIO2分别是阳极的氢气和氧气分压力；PHH2和PHO2分别是阴极的氢气和氧气分压力。当混合离子导体处于氧化气氛中，氧气与氧空位结合产生电子空穴。氢气在阳极催化作用下分解生成的电子与电子空穴结合，造成外部回路的电子数量减少。电子空穴的浓度可通过热力学平衡确定：

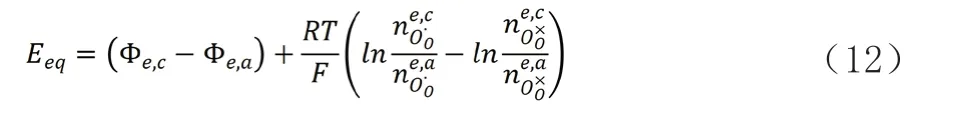
其中，(φe,c-φe,c)=△φe是电解质两端之间的静电势差；e,c和e,a分别表示阴极侧和阳极侧的电解质端部，是氧极化子。

(2)电解质中的电荷迁移

电荷载体x在混合离子导体中的运动可使用Nernst-Planck方程表达：

其中，Jm,x、Dx、nx、σx和zx分别表示电荷载体x的摩尔通量，扩散系数，离子浓度，电导率和电荷价态；q是元电荷；φ是静电势。Dk与σk之间的关系可以通过能斯特-爱因斯坦关系表达：

Zhang等人基于电子空穴电导均匀分布的假设，建立了考虑电流泄漏并假设四种电极反应的H-SOFCs电荷迁移框架，推导出了H-SOFCs泄漏电流的解析解：

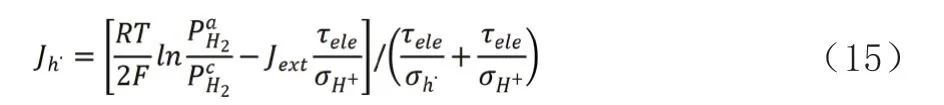
另一作者根据Zhang的H-SOFCs漏电模型，考虑了电解质中的电子空穴电导的非均匀分布，使得该模型更适用于各种工况。随后Putilov提出了一个新的计算模型来确定电流密度和在湿氢和湿氧工作的燃料电池的性能。发现有效质子电导率能够随着电池电压的上升而增加或减少，这取决于燃料和氧化剂哪边的湿度高。

图3 H-SOFCs电荷迁移框架

除了Nernst-Planck方程外，其他方程和模型也被用来研究混合离子导体中缺陷的运动。Virkar等人使用Goldman-Hodgkin-Katz方程和等效电路建立了混合离子导体作为电解质材料的SOFCs模型，该模型描述了电极-电解质界面中所有缺陷的迁移行为。后来Zhang等通过考虑各缺陷电导率随外部电压变化的情况，引入外电路电流密度作为自变量，改良现有的等效电路法，提出了更具普适意义的真实界面极化阻抗、欧姆阻抗和电子空穴阻抗数学表达式。

(3)过电势的计算

电解质存在一定的电阻，当质子电流流过时，不可避免地产生欧姆过电势，欧姆过电势可通过欧姆定律计算：

其中，JH+为质子电流密度；Lele为电解质厚度；σH+为质子电导率。

阳极和阴极的活化过电势与质子电流的关系可以用Butler-Volmer方程表示：

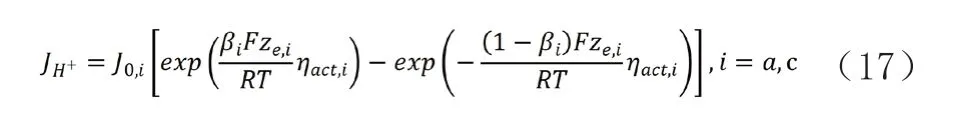
其中，βi为对称系数；ze,i为i的电子数；J0,i为交换电流密度。交换电流密度可由如下公式计算：

其中，γa和γc分别表示阳极和阴极的指数前因子；Eact,a和Eact,c分别表示阳极和阴极的活化能。

H-SOFCs的浓差过电势可以用电极表面和电极-电解质界面之间的气体浓度差表示：

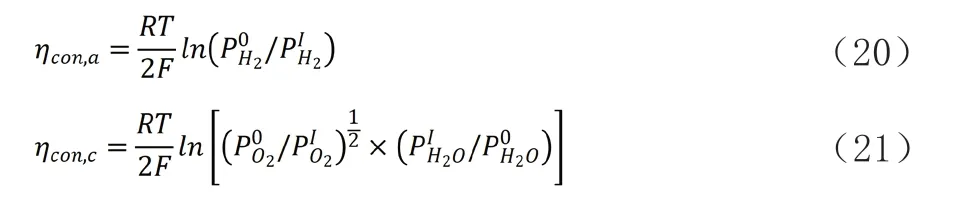
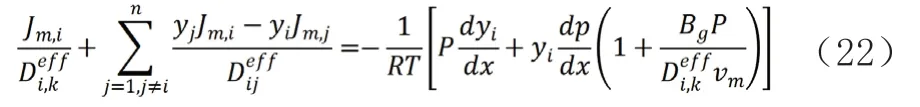
Patcharavorachot等人在计算浓差过电势时使用具有显式解析表达式的Fick模型，简化了气体在多孔电极中的运输。研究结果表明，H-SOFCs最佳的支撑结构为阳极支撑。这是因为阳极易于传输氢气，而阴极中的水蒸气和氧气扩散缓慢，较厚的阴极将会造成较高的浓差极化损失。

3.总结

质子导体固体氧化物燃料电池虽然拥有诸多优点，但是由于其本身电解质材料的特点导致的电流泄漏问题却不容忽视。虽然对单个H-SOFCs电池的建模研究已经有了一些初步成果，但是对于H-SOFCs电池堆的模拟研究还尚未出现。不同于单电池的模拟，电池堆的气体输送、电化学反应和热量传递等都是非常重要的，这就要求开发出更高层次的模型。