动静组合加载下不同负温人工冻结粉质黏土强度和变形特性分析

马冬冬， 马芹永， 黄 坤， 袁 璞， 姚兆明

(1. 安徽理工大学 矿山地下工程教育部工程研究中心, 安徽 淮南 232001; 2. 安徽理工大学 土木建筑学院, 安徽 淮南 232001)

冻土是一种典型的四相复合材料，冰的存在导致其强度和变形特性与未冻土明显不同[1]。研究认为，冻土的强度主要来源于冰胶结力、结构键结力和土颗粒间的黏聚力，其中，冰胶结力对冻土的物理力学特性影响最大[2]。崔托维奇[3]通过测量不同负温冻土内部的未冻水含量发现，冻土中的未冻水含量与有效含冰量处于动态平衡状态，温度的降低会导致冻土内部未冻水含量减少，但由于颗粒表面能的吸附作用，冻土中始终含有一定比例的未冻水。大量研究表明，温度是影响冻土未冻水含量最主要的因素[4-7]，为此，很多学者开展了静态和准静态应变率范围内(10-7～10-3s-1)不同负温冻土的力学性能试验，并取得了丰硕的研究成果。李鑫等[8-10]通过引入损伤和硬化因子用于反映温度引起的冻土强度变化，并提出了能够反映温度影响的冻土蠕变本构模型。张向东等[11]系统地分析了不同负温下冻土的动弹性模量退化特性。马芹永[12]研究表明，随着试验温度的降低，冻土的单轴抗压、抗拉强度逐渐增大，冻土的脆性特征明显增强，同时黄星等[13]的研究也得出了相似的结论，并且发现，相较于抗拉强度，冻土抗压强度的温度敏感性更为明显。

当遇到冻土爆破开挖破碎、考虑应力波作用的冻土体稳定性设计等工程问题时，低应变率范围内冻土的强度和变形参数已不能完全满足安全设计要求[14]，为此，很多学者采用分离式霍普金斯压杆(split Hopkinson pressure bar, SHPB)实验装置研究中高应变率(102～104s-1)范围内冻土的物理力学性质[15-18]。研究表明，温度、应变率和应力状态是影响冻土动态力学响应和破坏模式的重要因素，冲击荷载作用下，冻土内部裂纹萌生于冰晶体内部或土颗粒与冰晶体的边界等薄弱部位，冻土的动态强度和变形模量随着温度的降低和应变率的增加逐渐增大，并发现冻土破坏时表现出明显的“冻脆性”和“动脆性”特征。

马冬冬[19]通过分析冻土的工程受力状态得出，冻土在开挖破碎时所承受的荷载可分为以下两种类型：由上覆自重应力和地应力作用在冻土上的静荷载；以及由爆破应力波产生的动荷载，即承受动静组合受力状态，如图1所示。通过开展相同温度下，不同轴压和围压等级冻土的动态冲击压缩试验，发现冻土的动态强度和变形模量均随轴压比(轴压与冻土静态抗压强度的比值)的增加呈先增大后减小的变化趋势，且在0.7～0.8轴压比时强度达到峰值，随着围压的增加，冻土动态强度增长趋势逐渐变缓。总体来说，前期研究的焦点集中于单轴、被动围压、主动围压状态下人工冻土的动态强度和变形破坏特征[20-21]，但较少考虑冻土在实际工程中的动静组合受力状态，且没有对冻土的动态应力-应变曲线特征和变形模量等随温度的变化关系进行详细分析，此外，对于不同应力状态和应变率范围内温度对冻土力学性能影响的对比分析相对较少。

图1 冻土动静组合受力模型Fig.1 Coupled static and dynamic stress model of frozen soil

本文以冻结粉质黏土为研究对象，采用改进的SHPB试验装置，开展了不同负温条件下人工冻结粉质黏土的冲击压缩试验，重点对比分析了不同应力状态和应变率范围内，负温对人工冻结粉质黏土强度、变形模量和破坏特征的影响，以期为冻土工程安全快速掘进提供一定的试验基础。

1 动静组合SHPB装置及试验方案

1.1 冻结粉质黏土试样制备

试验用土取自山西某矿立井冻结粉质黏土，原状土样如图2所示，取样条件和基本物理性质如表1所示，考虑到原状土离散性较大，经实验室重塑后开展试验，重塑粉质黏土含水率和干密度与原状土相同，其颗粒级配如表2所示。试验时首先制备出所需尺寸的粉质黏土试样，然后将其放入-30 ℃的负温条件下快速冻结4～6 h，最后将其放入设定至试验温度的试验箱中冻结24 h以上。

图2 原状粉质黏土Fig.2 Undisturbed silty clay

表1 原状冻结粉质黏土取样条件和基本物理性质Tab.1 Sampling conditions and physical property of undisturbed silty clay

表2 重塑粉质黏土颗粒级配

1.2 动静组合SHPB试验装置

采用动静组合加载SHPB试验装置进行不同负温冻结粉质黏土的动态冲击试验，三维动静组合加载试验装置如图3所示，由加载系统、围压系统、轴压系统和数据处理系统组成。动静组合加载下人工冻土试验步骤已在相关文献进行详细介绍，在此不再阐述；对于采集到的原始波形信号采用简化的“三波法” 进行数据处理，以获取冻土的应力、应变和应变率；为满足冻土试样内部应力均匀，采用长径比为0.5(长度25 mm，直径50 mm)的冻土试样进行试验。

图3 动静组合SHPB试验装置[22]Fig.3 The modified triaxial SHPB device[22]

在开展动静组合加载试验的同时，采用WDT-100冻土压力试验系统来获取不同负温人工冻结粉质黏土的静态单轴强度和变形数据。试验时采用应变控制模式，根据MT/T593.8—2011《人工冻土物理力学性能试验》的推荐尺寸，人工冻结粉质黏土静态试验采用直径为50 mm，高度为100 mm的标准圆柱体试块。

1.3 试验方案

本次研究的目的是为了详细分析动静组合加载下负温对人工冻结粉质黏土强度与变形特性的影响，选取了8个温度等级，分别为-2 ℃、-5 ℃、-8 ℃、-10 ℃、-12 ℃、-15 ℃、-17 ℃和-20 ℃。动静组合加载下不同负温人工冻结粉质黏土试验方案如表3所示。在动态冲击试验中，对于不同负温的人工冻结粉质黏土，采用微调整冲击气压的方式以获得相近应变率。

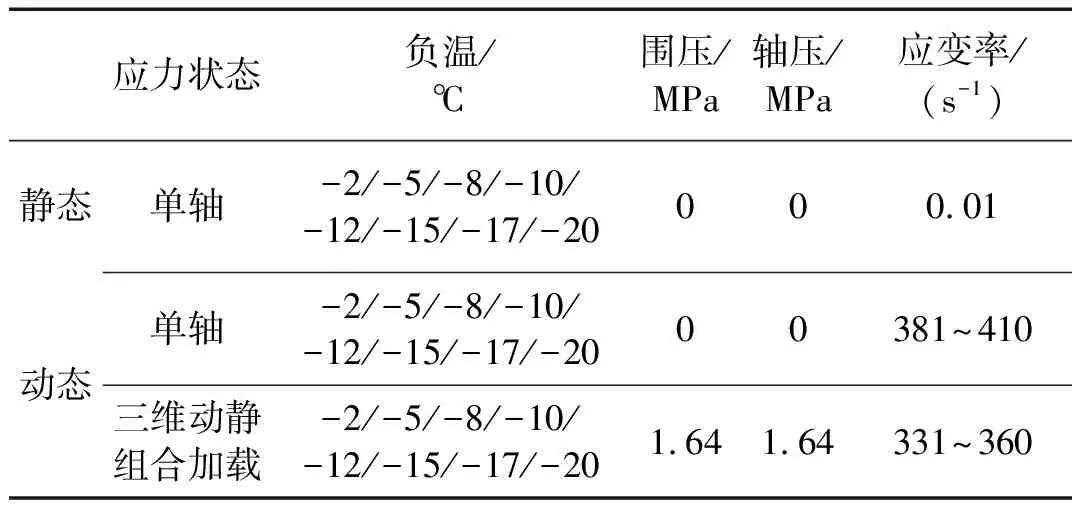
表3 动静组合加载下不同负温人工冻结粉质黏土试验方案

2 不同负温人工冻结粉质黏土应力-应变曲线

2.1 静态应力-应变曲线

根据设计的试验方案，首先分析了不同负温人工冻结粉质黏土的静态应力-应变特征，如图4所示。可以看出，对于-2和-5 ℃的人工冻结粉质黏土，静态应力-应变曲线无明显下降段，呈现明显的塑性特征，随着负温的降低，峰值应力逐渐提高，峰后下降段所占比例增大，曲线逐渐转化为脆性破坏特征。

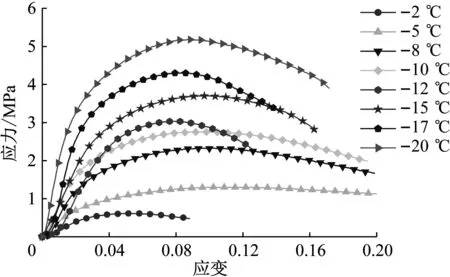
图4 不同负温人工冻结粉质黏土静态应力-应变曲线Fig.4 Static stress-strain curves of artificial frozen silty clay with various negative temperatures

2.2 动态应力-应变曲线

图5和图6分别为不同负温条件下，人工冻结粉质黏土在单轴和三维动静组合加载下的动态应力-应变曲线。

单轴状态下，-2 ℃时曲线压密和弹性阶段占比较大，达到峰值应力后曲线迅速下降。随着试验温度的降低，曲线弹性段占比有减少的趋势，峰后下降段逐渐趋于明显。三维动静组合加载下，不同负温冻土的应力-应变曲线变化趋势相似，均可划分为弹性、塑性和破坏三个阶段。

图5 不同负温人工冻结粉质黏土单轴动态应力-应变曲线

图6 三维动静组合加载下不同温度人工冻结粉质黏土动态 应力-应变曲线

3 不同负温人工冻结粉质黏土强度和变形模量

在冻土开挖破碎和支护工程中，温度越低，冻土开挖难度越大，而温度越高，冻土体稳定性越差[23]。因此，掌握不同负温冻土的强度和变形特性，对于提高破碎效率、确保冻土工程安全稳定有着重要的理论和工程意义。

3.1 静态和动态强度和变形模量确定方法

通过分析不同负温人工冻结粉质黏土的静态和动态应力-应变曲线特征，采用以下方法确定冻土的静态和动态强度和变形模量：静态和动态应力-应变曲线的峰值应力即静态和动态抗压强度；在单轴状态下，曲线弹性段斜率为静态和动态变形模量；在三维动静组合状态下，冻土应力-应变曲线特征与岩石类似，故参考动静组合状态下岩石两阶段变形模量的定义方法[24]，其中，第一阶段变形模量(E1)为50%抗压强度与坐标原点连线的斜率；第二阶段变形模量(E2)为抗压强度与50%抗压强度连线的斜率，如图7所示。

图7 三维动静组合加载下冻土变形模量的定义方法

3.2 不同负温人工冻结粉质黏土强度特性

图8为不同试验温度和应力状态下，本次试验得到的人工冻结粉质黏土的静态和动态抗压强度，同时，与参考文献[25]的试验数据进行对比分析。可以看出，随着温度的降低，冻土内部未冻水含量逐渐减少，其静态单轴、动态单轴、三维动静组合抗压强度均呈线性增大，其强度增长速率受到应力状态和应变率的共同影响，在本次试验条件下，增长速率由低到高依次为静态单轴、三维动静组合、动态单轴，说明人工冻结粉质黏土在冲击荷载作用下的温度敏感性要强于静态荷载，体现冻土的动脆性特征；在冲击荷载作用下，人工冻结粉质黏土在三维动静组合状态的温度敏感性要弱于单轴状态。相同负温条件下，人工冻结粉质黏土的抗压强度为静态单轴<动态单轴<三维动静组合。分析认为，在高应变率条件下，冻土内部裂纹数量和扩展速度都远大于低应变率，宏观上表现为应变率增强效应；冻土材料随着温度的降低逐渐变脆，这种脆性在冲击荷载作用下的表现则更加明显，导致在相同的温度变化范围内，动态强度的增幅要大于静态强度；此外，在围压和轴压的共同限制作用下，冻土的脆性无单轴状态下明显，导致三维动静组合状态的温度敏感性降低。

3.3 不同负温人工冻结粉质黏土变形模量

由于单轴和三维动静组合加载状态下变形模量的定义方法有所不同，下面分别进行分析。图9为单轴状态下，不同负温人工冻结粉质黏土的静态和动态变形模量，可以看出，随着试验温度的降低，静态和动态变形模量基本呈线性增长，且动态变形模量的增长速率大于静态；相同负温条件下，冻土的动态变形模量高于静态变形模量，说明在冲击荷载作用下，相同冻土变形对应的强度增量要大于静态荷载作用。图10为三维动静组合加载下，不同负温人工冻结粉质黏土的变形模量。研究表明，第一阶段的变形模量主要反映冻土在弹性段抵抗变形的能力，而第二阶段变形模量则体现出冻土抵抗塑性变形或损伤破裂的能力；相同负温变化条件下，第一阶段变形模量增长值要大于第二阶段变形模量，但二者增加幅度基本相同，随着温度的降低，冻土内部冰晶胶结能力逐渐增加，颗粒间黏结力增强，导致冻土在弹性和塑性段抵抗变形的能力均有所提高。

图8 不同试验温度人工冻结粉质黏土静态和动态抗压强度Fig.8 Static and dynamic compressive strengths of artificial frozen silty clay with various test temperatures

图9 单轴状态不同负温人工冻结粉质黏土变形模量

3.4 不同负温人工冻结粉质黏土增长系数

大量试验表明，岩石、混凝土、冻土等材料在高应变率范围内的强度或变形参数较低应变率有所提高，并通过定义强度增长因子等参数用于评价提升幅度[26-28]。通过以上分析可知，人工冻结粉质黏土也表现出类似的变化趋势，因此，定义强度增长系数IFσ和变形模量增长系数IFE，表达式为

(1)

(2)

式中：σdc和σsc分别为不同负温人工冻结粉质黏土动态和静态抗压强度；Ed和Ec分别为其对应的动态和静态变形模量。

图10 三维动静组合加载不同负温人工冻结粉质黏土变形模量

图11为计算得到的不同负温人工冻结粉质黏土强度增长系数和变形模量增长系数。IFE的值代表冻土在弹性阶段的变形速率，IFσ则反映冻土峰值应力的增长幅度，二者的大小宏观上体现了高应变率范围内(381～410 s-1)峰值应力和弹性段变形速率相较静载应变率(0.01 s-1)的提升幅度，可以看出，负温对单轴状态下冻土的IFσ和IFE影响不大，IFE的值在1.3～3.1之间波动，而IFσ的波动较小，其值在1.9～2.8范围内。

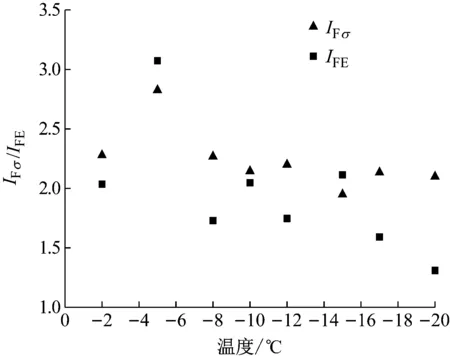
图11 不同负温人工冻结粉质黏土IFσ和IFE

3.5 不同负温人工冻结粉质黏土破坏特征

静态荷载作用下，不同负温人工冻结粉质黏土破坏模式主要呈剪切或“入”字型，如图12所示。动态单轴荷载作用下，冻土内部微裂隙和孔洞迅速扩展，并逐渐贯通演化成宏观裂纹，试样呈粉碎状破坏；而由于围压和轴压的限制作用，三维动静组合状态下冻土内部微裂隙的扩展程度明显降低，其环向和轴向变形量大幅度减少，试样在破坏后无明显裂纹，如图13所示。

(a) -10 ℃

(b) -20 ℃图12 不同负温人工冻结粉质黏土静态破坏模式Fig.12 Failure mode of artificial frozen silty clay with various negative temperatures under static load

(a) 单轴状态

(b) 三维动静组合状态图13 不同负温人工冻结粉质黏土动态破坏模式Fig.13 Failure mode of artificial frozen silty clay with various negative temperatures under dynamic load

4 结 论

(1) 随着温度的降低，人工冻结粉质黏土的静态单轴、动态单轴、三维动静组合抗压强度均呈线性增大，在本次试验条件下，增长速率由低到高依次为静态单轴、三维动静组合、动态单轴；相同负温下，人工冻结粉质黏土的抗压强度为静态单轴<动态单轴<三维动静组合。

(2) 人工冻结粉质黏土的静态和动态变形模量随着温度的降低基本呈线性增长，且动态变形模量的增长速率大于静态；相同负温变化条件下，第一阶段变形模量增长值要大于第二阶段变形模量，但二者增加幅度基本相同；负温对单轴状态下冻土的IFσ和IFE影响不大。